Leetcode.33 搜索旋转排序数组
题目链接
Leetcode.33 搜索旋转排序数组
mid
题目描述
整数数组 n u m s nums nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前, n u m s nums nums 在预先未知的某个下标 k ( 0 ≤ k < n u m s . l e n g t h ) k(0 \leq k < nums.length) k(0≤k<nums.length)上进行了 旋转,使数组变为 [ n u m s [ k ] , n u m s [ k + 1 ] , . . . , n u m s [ n − 1 ] , n u m s [ 0 ] , n u m s [ 1 ] , . . . , n u m s [ k − 1 ] ] [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] [nums[k],nums[k+1],...,nums[n−1],nums[0],nums[1],...,nums[k−1]](下标 从 0 0 0 开始 计数)。例如, [ 0 , 1 , 2 , 4 , 5 , 6 , 7 ] [0,1,2,4,5,6,7] [0,1,2,4,5,6,7] 在下标 3 3 3 处经旋转后可能变为 [ 4 , 5 , 6 , 7 , 0 , 1 , 2 ] [4,5,6,7,0,1,2] [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 n u m s nums nums 和一个整数 t t t ,如果 n u m s nums nums 中存在这个目标值 t t t,则返回它的下标,否则返回 − 1 -1 −1 。
你必须设计一个时间复杂度为 O ( l o g n ) O(log n) O(logn) 的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
提示:
- 1 ≤ n u m s . l e n g t h ≤ 5000 1 \leq nums.length \leq 5000 1≤nums.length≤5000
- − 1 0 4 ≤ n u m s [ i ] ≤ 1 0 4 -10^4 \leq nums[i] \leq 10^4 −104≤nums[i]≤104
- n u m s nums nums 中的每个值都 独一无二
- 题目数据保证 n u m s nums nums 在预先未知的某个下标上进行了旋转
- − 1 0 4 ≤ t a r g e t ≤ 1 0 4 -10^4 \leq target \leq 10^4 −104≤target≤104
解法:二分
n u m s nums nums 是一个排好序的数组,将其 旋转 之后,它仍然满足 两段性。
我们让 l = 0 , r = n − 1 , m i d = ( l + r ) / 2 l = 0 , r = n - 1 , mid = (l + r) / 2 l=0,r=n−1,mid=(l+r)/2。
1.如果此时 [ l , m i d ] [l,mid] [l,mid] 区间是是有序的:
- 如果 t t t 在区间 [ l , m i d ] [l,mid] [l,mid] 的范围内,也就是 n u m s [ l ] ≤ t ≤ n u m s [ m i d ] nums[l] \leq t \leq nums[mid] nums[l]≤t≤nums[mid],那么就可以缩减 r r r,即 r = m i d r = mid r=mid;
- 否则说明 t t t 不在这个区间内,那么就可以收缩 l l l,即 l = m i d + 1 l = mid + 1 l=mid+1;
2.如果此时 [ m i d + 1 , r ] [mid + 1,r] [mid+1,r] 区间是有序的:
- 如果 t t t 在区间 [ m i d + 1 , r ] [mid + 1,r] [mid+1,r] 的范围内,也就是 n u m s [ m i d + 1 ] ≤ t ≤ n u m s [ r ] nums[mid + 1] \leq t \leq nums[r] nums[mid+1]≤t≤nums[r],那么就可以缩减 l l l,即 l = m i d + 1 l = mid + 1 l=mid+1;
- 否则说明 t t t 不在这个区间内,那么就可以收缩 r r r,即 r = m i d r = mid r=mid;
时间复杂度: O ( l o g n ) O(logn) O(logn)
C++代码:
class Solution {
public:int search(vector<int>& nums, int t) {int n = nums.size();int l = 0 , r = n - 1;while(l < r){int mid = (l + r) >> 1;//这里必须为 nums[l] <= nums[mid]//因为 mid 是下取整的//如果当 nums 中的元素只有两个是 ,例如 nums = [3,1] , t = 1//此时 nums[l] 和 nums[mid] 都是同一个元素 即 3//如果不这样做的话 , 就会不满足这个判断进入到 else 的逻辑中 , 此时就会得出一个错误的答案if(nums[l] <= nums[mid]){if(nums[l] <= t && t <= nums[mid]) r = mid;else l = mid + 1;}else{if(nums[mid] < t && t <= nums[r]) l = mid + 1;else r = mid;}}return nums[l] == t ? l : -1;}
};
相关文章:

Leetcode.33 搜索旋转排序数组
题目链接 Leetcode.33 搜索旋转排序数组 mid 题目描述 整数数组 n u m s nums nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前, n u m s nums nums 在预先未知的某个下标 k ( 0 ≤ k < n u m s . l e n g t h )…...

ES 8.x 向量检索性能测试 把向量检索性能提升100倍!
向量检索不仅在的跨模态检索场景中应用广泛,随着chat gpt的或者,利用es的向量检索,在Ai领域发挥着越来越大的作用。 本文,主要测试es的向量检索性能。我从8.x就开始关注ES的向量检索了。当前ES已经发布到 8.10 版本。以下是官方文…...
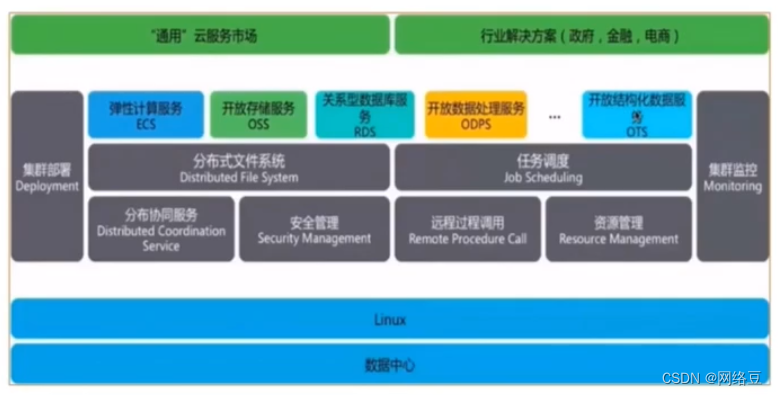
云计算——ACA学习 云计算架构
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 公众号:网络豆云计算学堂 座右铭:低头赶路,敬事如仪 个人主页: 网络豆的主页 目录 写在前面 前期回顾 本期介绍 一.云计算架…...
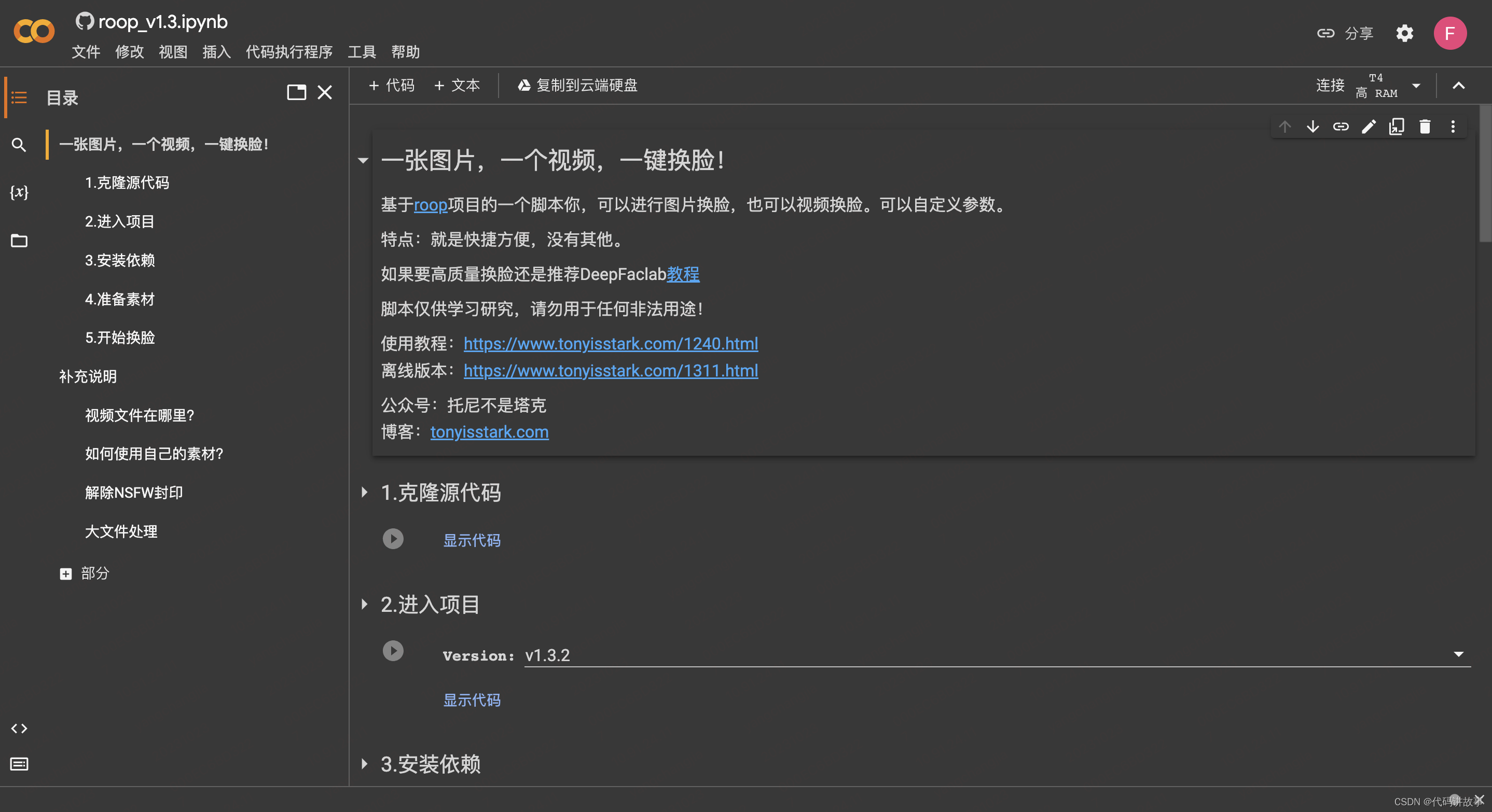
基于深度学习实现一张单图,一个视频,一键换脸,Colab脚本使用方法,在线版本,普通人也可以上传一张图片体验机器学习一键换脸
基于深度学习实现一张单图,一个视频,一键换脸,Colab脚本使用方法,在线版本,普通人也可以上传一张图片体验机器学习一键换脸。 AI领域人才辈出,突然就跳出一个大佬“s0md3v”,开源了一个单图就可以进行视频换脸的项目。 项目主页给了一张换脸动图非常有说服力,真是一图…...

leetcode 21
递归的方式 class Solution { public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {if(l1 nullptr){return l2;}else if(l2 nullptr){return l1;}else if(l1->val < l2->val){l1->next mergeTwoLists(l1->next, l2);return l1;}else if(l1->va…...
)
【Spring Cloud】openfeign负载均衡方案(和lb发展历史)
文章目录 版本1:原始loadBalancerClient方案版本2:ribbon-loadbalancer方案版本3:openfeign方案(即**方案2openfeign版本**) 本文描述了Spring Cloud微服务中,各个服务间调用的负载均衡方案的升级历史&…...

R语言:主成分分析PCA
文章目录 主成分分析处理步骤数据集code主成分分析 主成分分析(或称主分量分析,principal component analysis)由皮尔逊(Pearson,1901)首先引入,后来被霍特林(Hotelling,1933)发展。 主成分分析是一种通过降维技术把多个变量化为少数几个主成分(即综合变量)的统计分…...

Linux下磁盘备份、文件备份和定时备份命令指南
文章目录 磁盘备份和定时备份命令指南1. 引言2. 磁盘备份命令dda. 简介和基本用法b. dd命令的参数和选项说明c. 使用dd命令进行磁盘镜像备份的步骤d. 恢复备份数据的方法和注意事项e. 示例:使用dd命令备份和还原磁盘镜像 3. 磁盘备份命令tara. 简介和基本用法b. tar…...
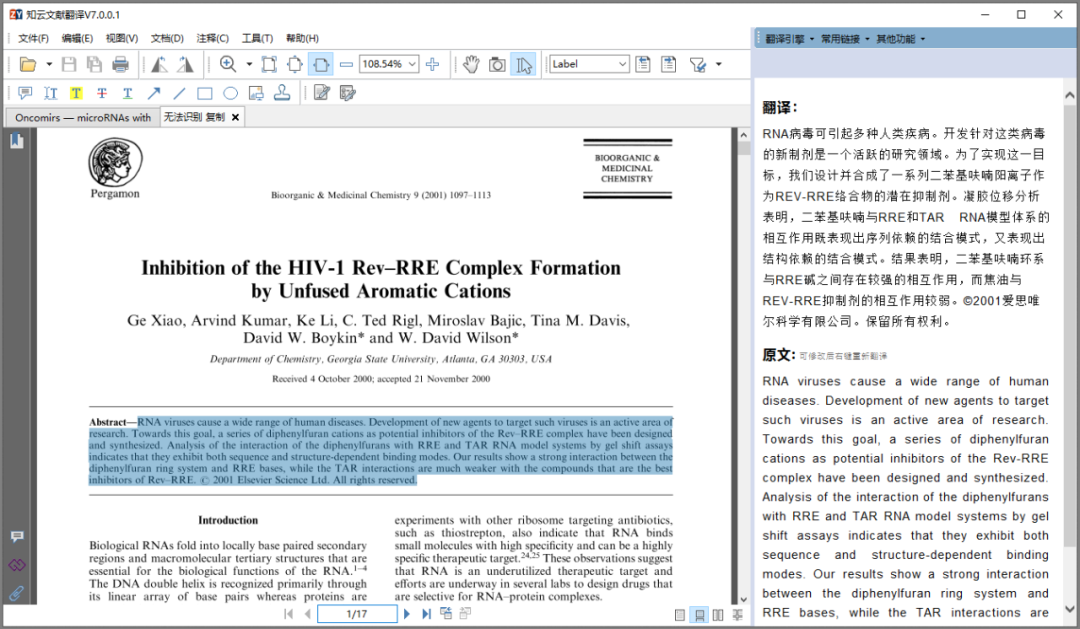
电脑软件:推荐一款非常强大的pdf阅读编辑软件
目录 一、软件简介 二、功能介绍 1、界面美观,打开速度快 2、可直接编辑pdf 3、非常强大好用的注释功能 4、很好用的页面组织和提取功能 5、PDF转word效果非常棒 6、强大的OCR功能 三、软件特色 四、软件下载 pdf是日常办公非常常见的文档格式,…...

Android 13.0 系统开机屏幕设置默认横屏显示
1.概述 在13.0的系统产品开发中,对于产品需求来说,由于是宽屏设备所以产品需要开机默认横屏显示,开机横屏显示这就需要从 两部分来实现,一部分是系统开机动画横屏显示,另一部分是系统屏幕显示横屏显示,从这两方面就可以做到开机默认横屏显示了 2.系统开机设置默认横屏显…...

Redis -- 基础知识1
1.介绍 1.初识Redis Redis:The open source, in-memory data store used by millions of developers as a database, cache, streaming engine, and message broker. in-memory data:在内存中存储,Redis是在分布式系统中存储起作用的 解释&am…...

ubuntu 20.04 passwd 指令不能使用
Linux 更改用户密码报Changing password for user 用户名. passwd: Module is unknown或更改新增用户密码passwd:未知的用户名 报错信息如下: 解决方法: 可以排查 /etc/pam.d/passwd配置文件 注释掉包含pam_passwdqc.so模块的行,…...
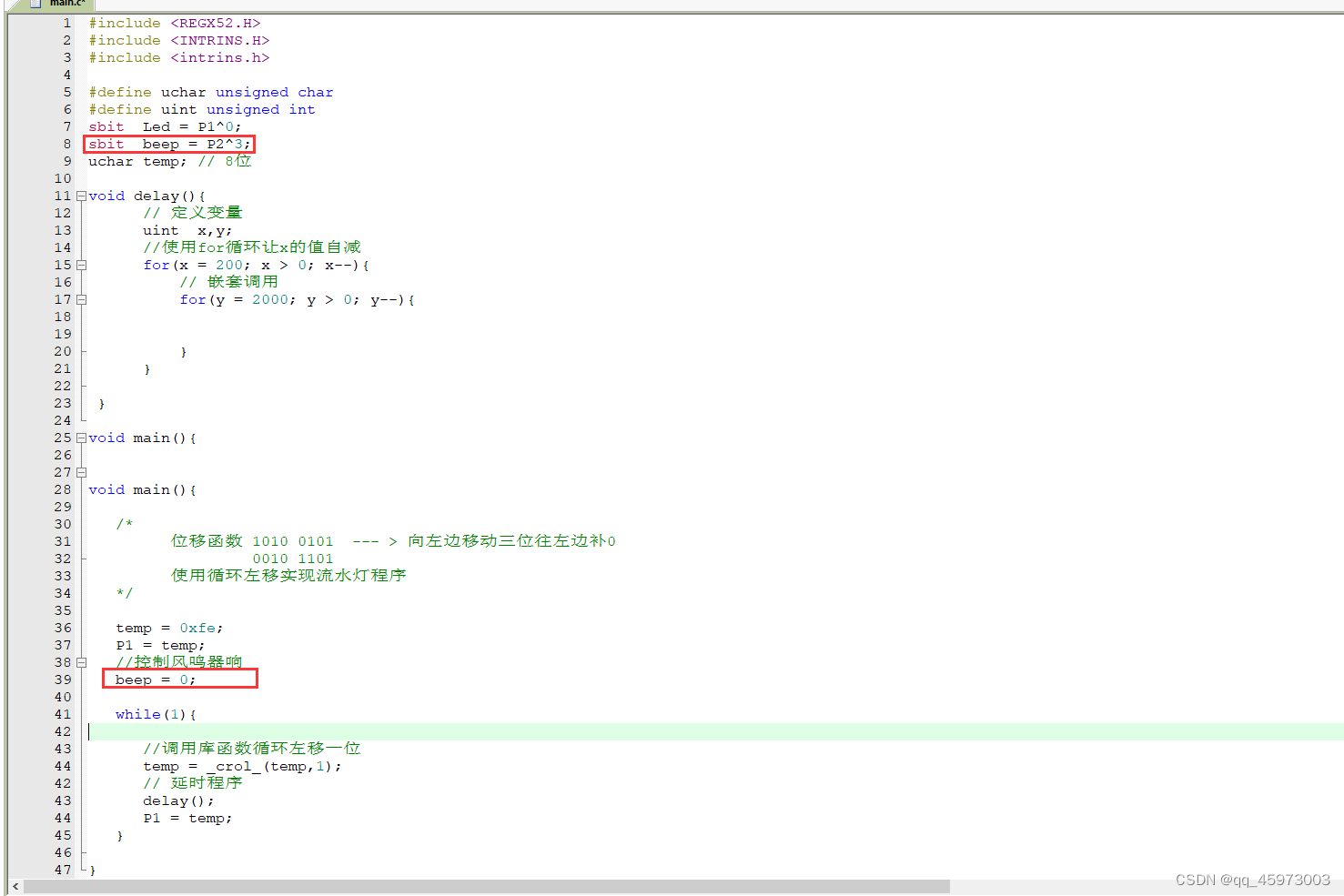
单片机郭天祥(02)
1:解决keil5软件的乱码问题,修改编码为UTF-8 2:打开keil5使用debug对编写好的程序进行调试 给程序打上断点 使用仿真芯片 更改设备管理器相关设置 接通电源后点击debug连接到51单片机 使用stc-isp获取延时函数 将延时函数添加进入创建好的…...

Hadoop3教程(三十五):(生产调优篇)HDFS小文件优化与MR集群简单压测
文章目录 (168)HDFS小文件优化方法(169)MapReduce集群压测参考文献 (168)HDFS小文件优化方法 小文件的弊端,之前也讲过,一是大量占用NameNode的空间,二是会使得寻址速度…...

metersphere 接口自动化
Metersphere 使用步骤大致如下: 安装 Metersphere Metersphere 是一款基于 Docker 的应用程序,因此在使用 Metersphere 之前,需要先安装 Docker。安装 Docker 后,再下载 Metersphere 的安装包并解压缩。 启动 Metersphere 在终…...

Mac上安装和配置Git
在Mac上安装和配置Git是一个相对简单的过程,以下是一份详细的步骤指南。 首先,你需要确保你的Mac已经安装了Homebrew(如果还没有安装,可以通过以下命令安装:),Homebrew是一个包管理器ÿ…...

【文件操作】Java -操作File对象
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 文件操作 Java - File对象 Java - File对象 Fi…...

Socks5代理技术:驱动数字化时代跨界发展的利器
随着全球数字化进程的加速推进,Socks5代理技术作为一项关键的网络技术正日益成为推动跨界电商、爬虫数据分析、企业出海以及游戏体验优化等领域发展的重要驱动力。其高效稳定的网络连接能力以及灵活的应用方式,不仅为企业提供了全球市场拓展的无限可能&a…...

基于二维小波变换的散斑相位奇异构造算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 图(1)表示散斑原图像,(2)表示对(1)图像进行x轴方向的极化分析的小波相位图,呈周期的水平条纹,(3)表示对(1)图像…...

为啥么有奖章
6.1 域名系统 DNS 应用层的许多协议都是基于客户服务器方式。即使是 P2P 对等通信方式,实质上也是一种特殊的客户服务器方式。这里再明确一下,客户(client)和服务器(server)都是指通信中所涉及的两个应用进程。客户服务器方式所描述的是进程之间服务和被…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...
数据可视化交互
目录 【实验目的】 【实验原理】 【实验环境】 【实验步骤】 一、安装 pyecharts 二、下载数据 三、实验任务 实验 1:AQI 横向对比条形图 代码说明: 运行结果: 实验 2:AQI 等级分布饼图 实验 3:多城市 AQI…...

AI书签管理工具开发全记录(十八):书签导入导出
文章目录 AI书签管理工具开发全记录(十八):书签导入导出1.前言 📝2.书签结构分析 📖3.书签示例 📑4.书签文件结构定义描述 🔣4.1. 整体文档结构4.2. 核心元素类型4.3. 层级关系4.…...

TI德州仪器TPS3103K33DBVR低功耗电压监控器IC电源管理芯片详细解析
1. 基本介绍 TPS3103K33DBVR 是 德州仪器(Texas Instruments, TI) 推出的一款 低功耗电压监控器(Supervisor IC),属于 电源管理芯片(PMIC) 类别,主要用于 系统复位和电压监测。 2. …...
