算法进阶——数组中的逆序对
题目
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P mod 1000000007
数据范围:对于 50% 的数据, size≤104
对于 100% 的数据, size≤105
数组中所有数字的值满足 0≤val≤109
要求:空间复杂度O(n),时间复杂度O(nlogn)
输入描述:
题目保证输入的数组中没有的相同的数字
示例1
输入:
[1,2,3,4,5,6,7,0]
返回值:
7
示例2
输入:
[1,2,3]
返回值:
0
思路
这题可以用归并统计法,也就是在归并排序的同时进行统计。
先了解归并排序算法,主要思想是先分后并:
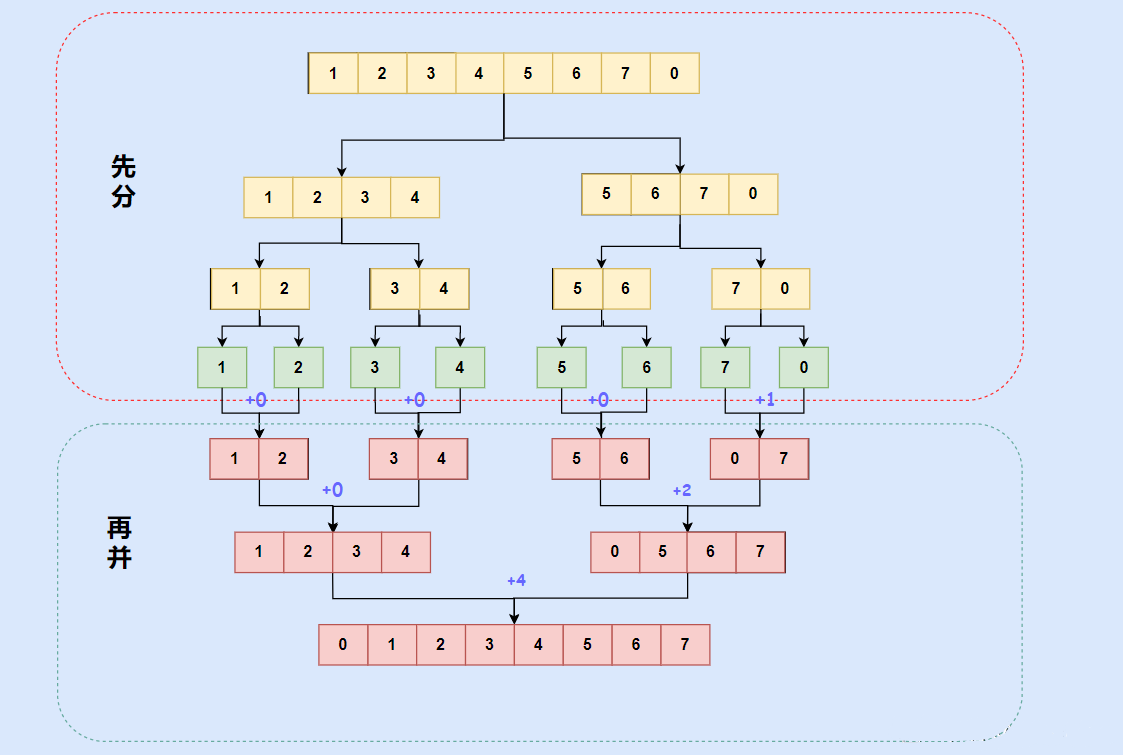
- 将数组分为两个子数组,两个子数组分为四个子数组,依次向下分,直到数组不能再分为止。
- 从最小的数组按照顺序合并,从小到大或从大到小,依次向上合并,最后得到合并完的顺序数组。
归并统计法,关键点在于合并环节,在合并数组的时候,当发现右边的小于左边的时候,此时可以直接求出当前产生的逆序对的个数。
举个例子:
在合并 {4 ,5} {1 , 2} 的时候,首先我们判断 1 < 4,我们即可统计出逆序对为2,为什么呢?这利用了数组的部分有序性。因为我们知道 {4 ,5} 这个数组必然是有序的,因为是合并上来的。此时当 1比4小的时候,证明4以后的数也都比1大,此时就构成了从4开始到 {4,5}这个数组结束,这么多个逆序对(2个),此时利用一个临时数组,将1存放起来,接着比较2和4的大小,同样可以得到有2个逆序对,于是将2也放进临时数组中,此时右边数组已经完全没有元素了,则将左边剩余的元素全部放进临时元素中,最后将临时数组中的元素放进原数组对应的位置。
可以看到下面这张图:
解答代码
class Solution {
public:/*** @param nums int整型vector * @return int整型*/int InversePairs(vector<int>& nums) {// write code hereint res = 0;vector<int> tmp(nums.size());MergeSort(nums, tmp, 0, nums.size() - 1, res);return res;}void MergeSort(vector<int>& nums, vector<int>& tmp, int left, int right, int& res) {// 递归结束if (left >= right) {return;}// 中心点int mid = left + (right - left) / 2;// 归并MergeSort(nums, tmp, left, mid, res);MergeSort(nums, tmp, mid + 1, right, res);Merge(nums, tmp, left, mid, right, res);}void Merge(vector<int>& nums, vector<int>& tmp, int left, int mid, int right, int& res) {int i = left; // 左子数组下标起点int j = mid + 1; // 右子数组下标起点int k = 0; //临时数组的下标起点while (i <= mid && j <= right) {if (nums[i] < nums[j]) {// 左子数组元素当前元素较小,无逆序,只进行排序tmp[k++] = nums[i++];} else {// 左子数组元素当前元素较大,排序同时记录逆序数tmp[k++] = nums[j++];res += mid + 1 - i;res %= 1000000007; // 应题目要求}}// 子数组中剩下元素全部存入临时数组while (i <= mid) {tmp[k++] = nums[i++];}while (j <= right) {tmp[k++] = nums[j++];}// 完成排序for (int i = left, j = 0; i <= right; i++, j++) {nums[i] = tmp[j];}}
};
相关文章:

算法进阶——数组中的逆序对
题目 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P mod 1000000007 数据范围:对于 50% 的数据, size≤104 对…...
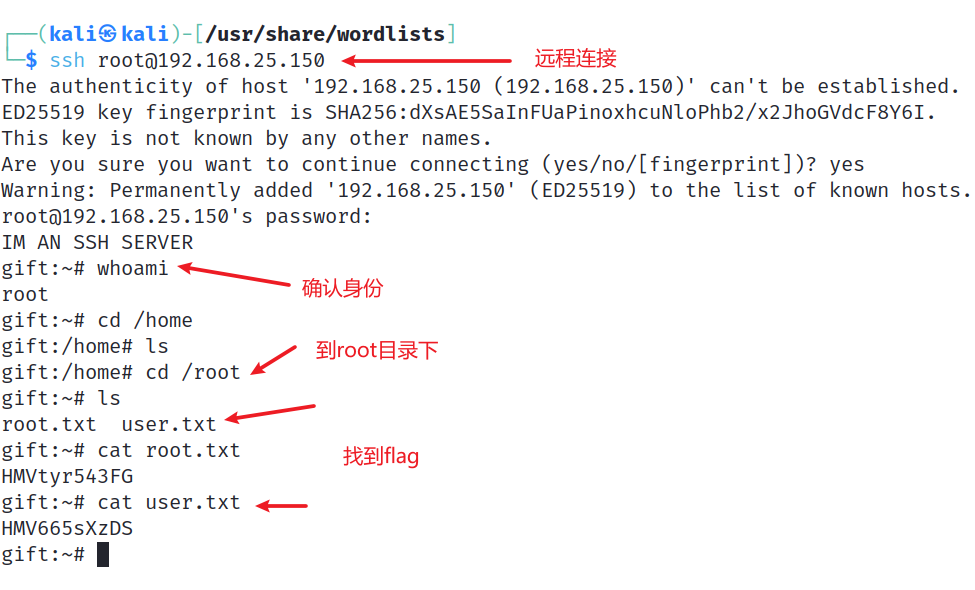
hackmyvm之gift
hackmyvm是一个平台,包含了大量靶机,类似于vulnhub、hackthebox等平台,你可以在上面下载靶机,进行渗透测试练习,非常适合热爱黑客技术或从事渗透测试的人员。 (这段解释参考这篇文章) 下载安装…...

1024,向着“顶尖程序员“迈进
10月24日,对每个程序员而言,都是一个具有特殊意义的日子。1024这个数字,不再只是计算机存储容量的基础单位,更是我们向着技术巅峰进发的象征。 回顾我的程序员之路,那是一个不断学习、不断成长的过程。起初是对编程充…...

Arcgis 数据操作
在进行数据操作的时候,需要注意坐标系要一致,这是前提。 数据类型 文件地理数据库:gbd 个人地理数据库:mdb (Mircosoft Access) 矢量数据:shp 推荐使用gbd数据,效率会更高。 采…...

YoloV7改进策略:SwiftFormer,全网首发,独家改进的高效加性注意力用于实时移动视觉应用的模型,重构YoloV7
文章目录 摘要论文:《SwiftFormer:基于Transformer的高效加性注意力用于实时移动视觉应用的模型》1、简介2、相关研究3、方法3.1、注意力模块概述3.2、高效的加性注意力3.3、SwiftFormer 架构4、实验4.1、实现细节4.2、基线比较4.3、图像分类4.4、目标检测和实例分割4.5、语义…...
Day07 Stream流递归Map集合Collections可变参数
Stream 也叫Stream流,是Jdk8开始新增的一套API (java.util.stream.*),可以用于操作集合或者数组的数据。 Stream流大量的结合了Lambda的语法风格来编程,提供了一种更加强大,更加简单的方式操作 public class Demo1 {public stati…...

8.JavaScript-注释
题记 javascript注释 单行注释 <!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>实例</title> </head> <body><h1 id"myH1"></h1> <p id"myP"></p>…...

知识分享|分段函数线性化及matlab测试
目录 1 使用0-1变量将分段函数转换为线性约束 2 连续函数采用分段线性化示例 3 matlab程序测试 4 matlab测试结果说明 5 分段线性化应用 1 使用0-1变量将分段函数转换为线性约束 2 连续函数采用分段线性化示例 3 matlab程序测试 clc;clear all; gn10;tn1; x_pfsdpvar(1, t…...

ant target的depends属性
ant的target使用depends属性指明对其它target的依赖。可以依赖多个target,被依赖的多个target之间用逗号分隔。 ant会确保被依赖的target首先执行,然后再执行本target。 ant尽量按照depends属性中指明的target出现的顺序来执行(从左到右&…...
【三维重建】DreamGaussian:高斯splatting的单视图3D内容生成(原理+代码)
文章目录 摘要一、前言二、相关工作2.1 3D表示2.2 Text-to-3D2.3 Image-to-3D 三、本文方法3.1生成式 高斯 splitting3.2 高效的 mesh 提取3.3 UV空间的纹理优化 四. 实验4.1实施细节4.2 定性比较4.3 定量比较4.4 消融实验 总结(特点、局限性) 五、安装与…...

如何使用Flutter开发执行操作系统shell命令的工具
简介 Flutter是一种由Google开发的移动应用程序开发框架,它允许开发人员使用单个代码库构建高性能、高质量的移动体验。而Android终端命令行工具则允许用户在Android手机上运行类似于Linux的操作系统命令。本文的目的是介绍如何在Flutter应用中开发一个Android终端命…...

西山居 游戏研发工程师实习生 面经
西山居实习面经 面试时长:26min(两个面试官交替问) 1、自我介绍 2、你平常怎么学习的 3、你实习接受加班么 4、说一下Unity的生命周期,Start和Awake哪里不同 5、Unity中Update与FixedUpdate的区别,怎么设置Fixed…...
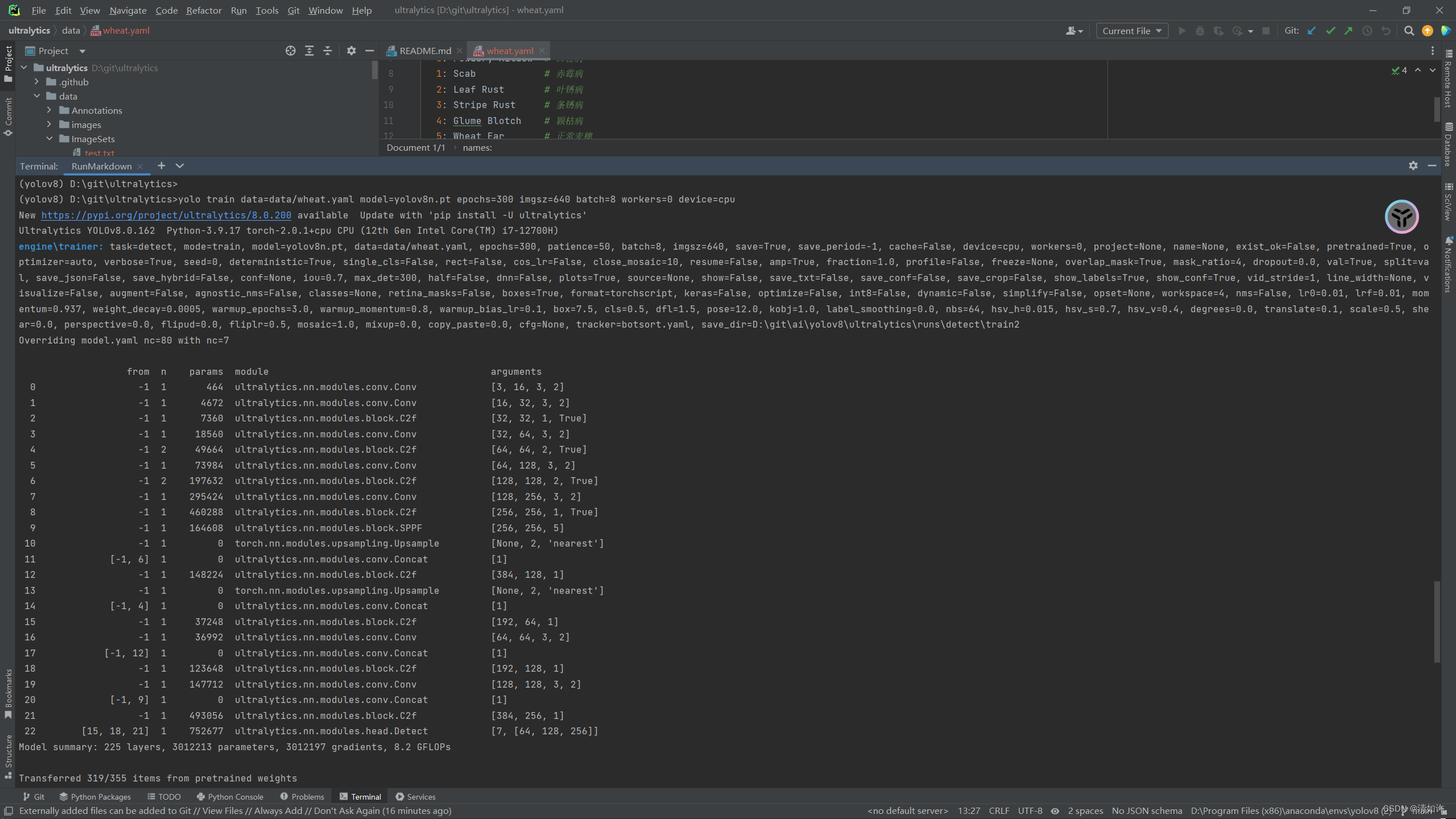
YOLOv8训练自己的数据集+改进方法复现
yolov8已经出来好几个月了,并且yolov8从刚开始出来之后的小版本也升级好几次,总体变化不大,个别文件存放位置发生了变化,以下以最新版本的YOLOv8来详细学习和使用YOLOv8完成一次目标检测。 一、环境按照 深度学习环境搭建就不再…...
尚硅谷kafka3.0.0
目录 💃概述 ⛹定义 编辑⛹消息队列 🤸♂️消息队列应用场景 编辑🤸♂️两种模式:点对点、发布订阅 编辑⛹基本概念 💃Kafka安装 ⛹ zookeeper安装 ⛹集群规划 编辑⛹流程 ⛹原神启动 🤸♂️…...

【Andriod】Appium的不同版本(Appium GUI、Appium Desktop、Appium Server )的安装教程
文章目录 前言一.Appium GUI二.Appium Desktop三.Appium Server 命令行版本1.安装node.js2.安装Appium Server 前言 Appium 安装提供两2方式:桌面版和命令行版。其中桌面版又分为 Appium GUI 和 Appium Desktop。 建议:使用Appium Desktop 一.Appium …...

leetcode:面试题 17.04. 消失的数字(找单身狗/排序/公式)
一、题目: 函数原型:int missingNumber(int* nums, int numsSize) 二、思路: 思路1 利用“找单身狗”的思路(n^n0;0^nn),数组中有0-n的数字,但缺失了一个数字x。将这些数字按位异或0…...
基于SpringBoot的时间管理系统
基于SpringBoot的时间管理系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringBootMyBatis工具:IDEA/Ecilpse、Navicat、Maven 系统展示 登录界面 管理员界面 用户界面 摘要 基于Spring Boot的时间管理系统是一款功能丰富…...

centos搭建elastic集群
1、环境可以在同一台集群上搭建elastic,也可以在三台机器上搭建,这次演示的是在同一台机器搭建机器。 2、下载elastic :https://www.elastic.co/cn/downloads/past-releases#elasticsearch 2、 tar -zxvf elasticsearch-xxx-版…...
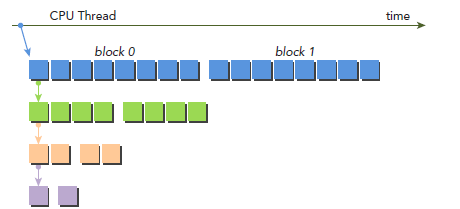
CUDA学习笔记(九)Dynamic Parallelism
本篇博文转载于https://www.cnblogs.com/1024incn/tag/CUDA/,仅用于学习。 Dynamic Parallelism 到目前为止,所有kernel都是在host端调用,CUDA Dynamic Parallelism允许GPU kernel在device端创建调用。Dynamic Parallelism使递归更容易实现…...

周记之马上要答辩了
“ 要变得温柔和强大,就算哪天突然孤身一人,也能平静地活下去,不至于崩溃。” 10.16 今天提前写完了一篇六级阅读,积累了一些词组: speak out against 公然反对,印象最深刻的就这个; 先了解…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...
