完全背包问题
目录
1. 朴素解法
2. 优化
原题链接:
3. 完全背包问题 - AcWing题库
题目描述:
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行两个整数 vi, wi,用空格隔开,分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0< N, V ≤10000
0< vi, wi ≤ 1000输入样例
4 5 1 2 2 4 3 4 4 5输出样例:
10
在解决这道题之前我们先来回顾一下 Acwing 的讲师:y总,他讲述的解决动态规划问题的一般步骤 。
集合:表示状态中每一个下标位置可能的选择。一维数组也好二维数组也罢,动态规划处理之后里面存储的元素就是这个状态下对应的最终结果。而这个结果的产生,就是集合中满足题意的那个元素。属性:属性需要根据题意来选择。就拿本题来说,要计算价值的最大值,那么属性就是集合中价值的最大值!
状态计算:将每一个状态中的集合进行划分,根据集合的划分推出状态转移方程。
集合划分的依据:划分出来的所有集合的并集不得遗漏一个状态中的任何选择。但是可以重复。
1. 朴素解法
这道题的状态表示和 01 背包问题里面的状态表示相同。
状态表示中的集合:从 1 - i 个物品中选,并且物品的总体积不超过 j 的所有选法!
状态表示中的属性:集合中所有选法的价值最大值。
我想,你现在对 集合 与 属性的关系一定有了自己的理解!动态规划存储结果的数组中的一个元素都是该状态下的集合中满足一定属性的那个值!
下面我们来看状态计算:我们在 01 背包问题中,将集合划分成了是否选择第 i 个物品两个部分。我们可以借鉴 01 背包问题的思路。
完全背包问题中,我们将集合划分为:
第 i 个物品选择 0 个,
第 i 个物品选择 1 个,
第 i 个物品选择 2 个,
······,
第 i 个物品选择 k 个
若干个部分。
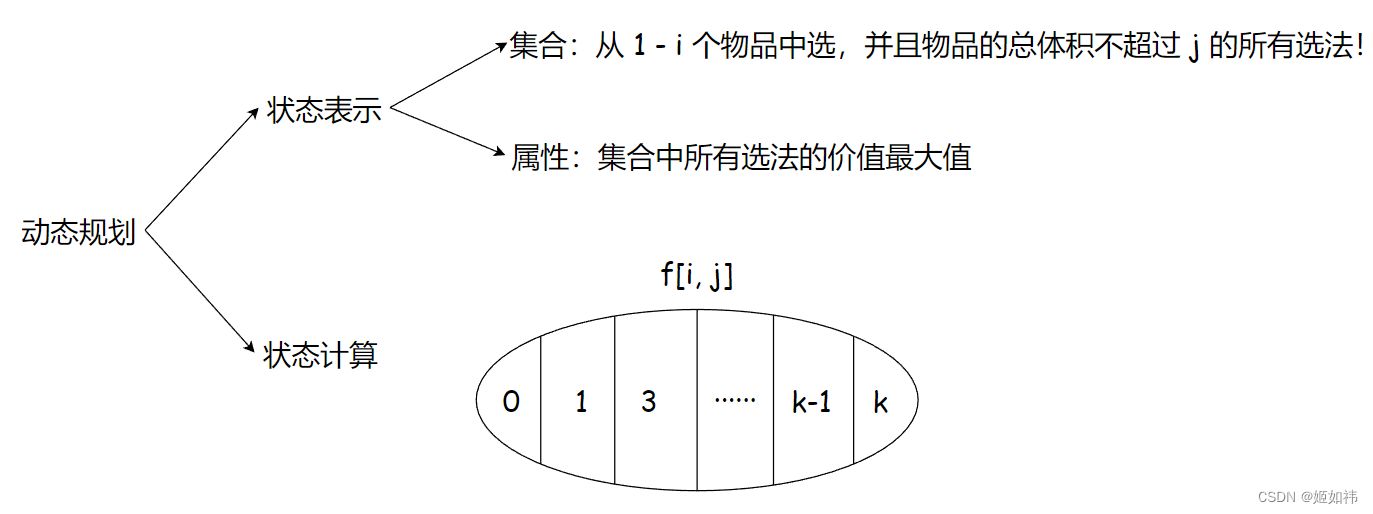
根据上图,我们将集合划分成了若干部分,并且如此划分集合满足集合划分的依据,下一步要做的就是推导出状态转移方程,即如何计算出集合中价值的最大值。
同时我们还注意到: k 不能胡乱取值,因为我们的背包体积是有限的,当 k * v[i] 大于 背包的体积,此时往后的 k 都是无效的。
下面我们来推导状态转移方程:
我们不妨假设第 i 个物品我们选择了 k 个。
当 k = 0 时,说明不选择第 i 个物品,此时 f [i, j] = f [i - 1, j],这倒是很简单!
当 k 不等于 0 时该怎么办呢?同样借鉴一下 01 背包问题的想法:之前假设第 i 个物品选择了 k 个,我们可以先不看第 i 个物品,那么问题就变成了从 1 - (i - 1) 中的物品中做选择,但是选择的体积还是不大于 j 吗?当然不是,因为我们忽略了第 i 个物品,并且我们选择了 k 个第 i 个物品,因此选择的总体积应该是不大于 j - k * v[i],(v[i] 是第 i 个物品的体积)。
那么当 k 不等于 0 时,状态转移方程就可以写成:f [i, j] = f [ i - 1][ j - k * v[i] ] + k * w[i]。这里为什么要加上 k * w[i] 呢?因为 f [ i - 1][ j - k * v[i] ] 是忽略了第 i 个物品的选择的价值最大值,想要计算 f [ i, j ] 肯定要算上第 i 个物品的选择嘛!
最后我们惊奇的发现,k = 0 与 k != 0,f [i, j] 都等于 f [ i - 1][ j - k * v[i] ] + k * w[i]。
因为要求的是价值的最大值,因此在遍历 k 的取值时要取价值最大的那一个!
#include<iostream>
#include<algorithm>
using namespace std;const int N = 1010;
int v[N], w[N];
int f[N][N];
int n, m;int main()
{cin >> n >> m;for(int i = 1; i <= n; i++)cin >> v[i] >> w[i];for(int i = 1; i <= n; i++){for(int j = 0; j <= m; j++){for(int k = 0; k * v[i] <= j; k++){f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);}}}cout << f[n][m] << endl;return 0;
}2. 优化
优化的味道有点向数学,我们需要将 f[i, j] 的状态转移方程展开:
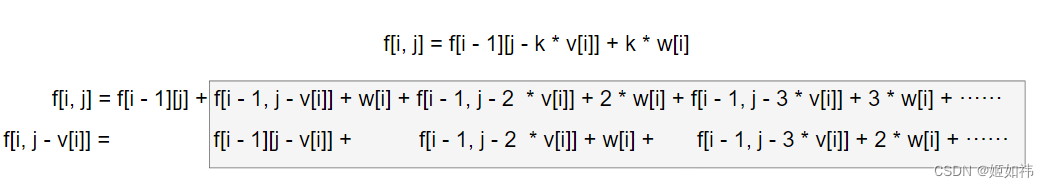
我们发现灰色的那一坨是差不多的,就差了一个 w[i],因此我们的状态转移方程可以修改为:
f[i, j] = max( f[i - 1][j] + f[i, j - v[i]] + w[i] )
#include<iostream>
#include<algorithm>
using namespace std;const int N = 1010;
int v[N], w[N];
int f[N][N];
int n, m;int main()
{cin >> n >> m;for(int i = 1; i <= n; i++)cin >> v[i] >> w[i];for(int i = 1; i <= n; i++){for(int j = 0; j <= m; j++){f[i][j] = f[i - 1][j];if(j >= v[i])f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);}}cout << f[n][m] << endl;return 0;
}再根据 01 背包问题的空间优化,完全背包问题的空间也是可以优化到一维的,并且根据状态转移方程,从小到大枚举并无问题,因为 j - v[i] 一定在之前被计算过,因此,完全背包问题的最终代码:
#include<iostream>
#include<algorithm>
using namespace std;const int N = 1010;
int v[N], w[N];
int f[N];
int n, m;int main()
{cin >> n >> m;for(int i = 1; i <= n; i++)cin >> v[i] >> w[i];for(int i = 1; i <= n; i++)for(int j = v[i]; j <= m; j++)f[j] = max(f[j], f[j - v[i]] + w[i]);cout << f[m] << endl;return 0;
}相关文章:
完全背包问题
目录 1. 朴素解法 2. 优化 原题链接: 3. 完全背包问题 - AcWing题库 题目描述: 有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。 第 i 种物品的体积是 vi,价值是 wi。 求解将哪些物品装入背包,可使这些…...
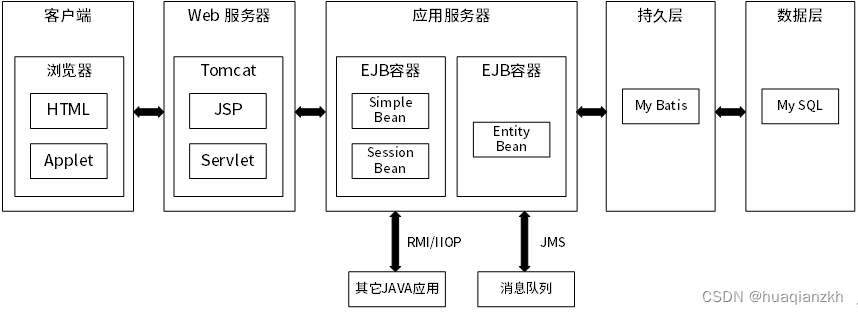
J2EE的N层体系结构
J2EE平台采用了多层分布式应用程序模型,实现不同逻辑功能的应用程序被封装到不同的构件中,处于不同层次的构件可被分别部署到不同的机器中。 RMI/IIOP:RMI(Remote Method Invocation,远程方法调用)是Java的…...

Quirks(怪癖)模式是什么?它和 Standards(标准)模式有什么区别?
目录 前言: 用法: 代码: Quirks模式示例: Standards模式示例: 理解: Quirks模式: Standards模式: 高质量讨论: 前言: "Quirks模式"和"Standards模式"是与HTML文档渲染模式相关的两种模式。它们影响着浏览器如何解释和渲染HT…...
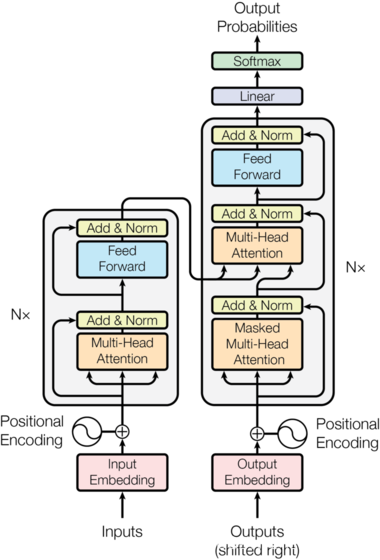
自然语言处理---Transformer模型
Transformer概述 相比LSTM和GRU模型,Transformer模型有两个显著的优势: Transformer能够利用分布式GPU进行并行训练,提升模型训练效率。 在分析预测更长的文本时,捕捉间隔较长的语义关联效果更好。 Transformer模型的作用 基于seq…...
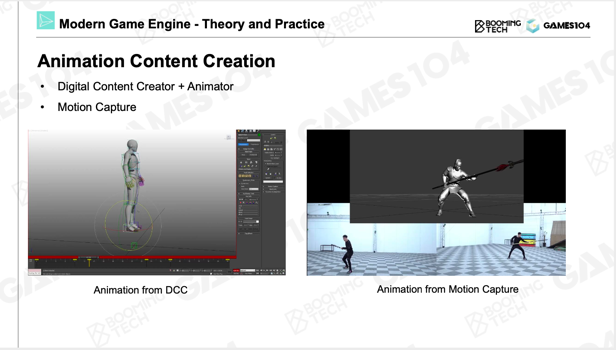
动画系统的前世今生(一)
掐指一算,五年没更新过我的CSDN账号啦,方向也从人工智能变成了计算机图形学,当然也依旧会关注AI的发展,之前在知乎上写了一些文章[传送门],后续也会逐渐同步到CSDN上~ 这个系列将包含五篇文章,内…...

11 结构型模式- 代理模式
结构性模式一共包括七种: 代理模式、桥接模式、装饰者模式、适配器模式、门面(外观)模式、组合模式、和享元模式。 1 代理模式介绍 软件开发中的代理: 代理模式中引入了一个新的代理对象,代理对象在客户端对象和目标对象之间起到了中介的作用,它去掉客…...
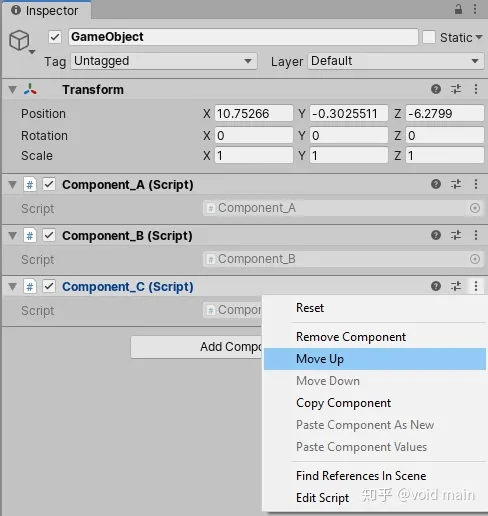
Unity--用户界面
目录 “使用工具栏”: “层次结构”窗口: 层次结构窗口 制作子GameObject “游戏”视图: “场景视图“: ”项目窗口“: 项目窗口工具栏: "Inspector" 窗口: Inspector 游戏…...

BUUCTF 乌镇峰会种图 1
BUUCTF:https://buuoj.cn/challenges 题目描述: 乌镇互联网大会召开了,各国巨头汇聚一堂,他们的照片里隐藏着什么信息呢?(答案格式:flag{答案},只需提交答案࿰…...

Runner GoUI自动化测试发布
构建自动化测试体系是当下每个项目团队愿意去做的,自动化测试减少重复操作节省人力成本。 RunnerGo UI自动化平台 RunnerGo提供从API管理到API性能再到可视化的API自动化、UI自动化测试功能模块,覆盖了整个产品测试周期。 RunnerGo UI自动化基于Selen…...

【Gensim概念】03/3 NLP玩转 word2vec
第三部分 对象函数 八 word2vec对象函数 该对象本质上包含单词和嵌入之间的映射。训练后,可以直接使用它以各种方式查询这些嵌入。有关示例,请参阅模块级别文档字符串。 类型 KeyedVectors 1) add_lifecycle_event(event_name, log_level2…...
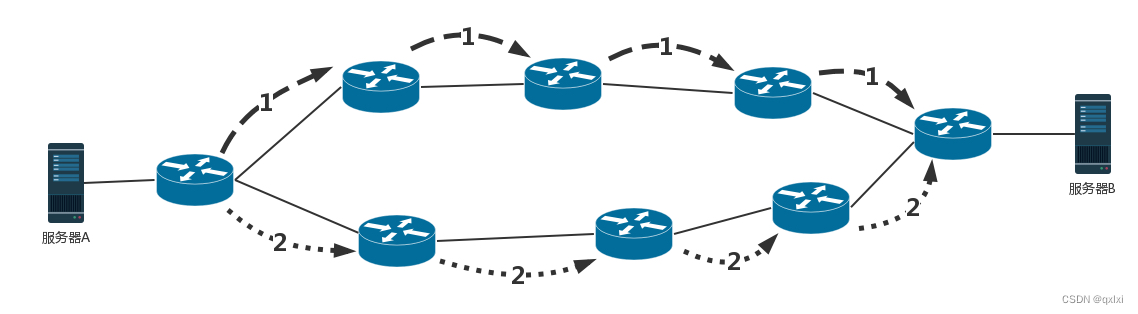
【网络协议】聊聊网络路由相关算法
如何配置路由 路由器是一台网络设备,多张网卡,当一个入口的网络包到达路由器时,会根据本地的信息库决定如何正确的转发流量,通常称为路由表 路由表主要包含如下 核心思想是根据目的 IP 地址来配置路由 目的网络:要去…...

Python 深度学习入门之CNN
CNN 前言一、CNN简介1、简介2、结构 二、CNN简介1、输出层2、卷积层3、池化层4、全连接层5、输出层 前言 1024快乐!1024快乐!今天开新坑,学点深度学习相关的,说下比较火的CNN。 一、CNN简介 1、简介 CNN的全称是Convolutiona…...

国产开发板上打造开源ThingsBoard工业网关--基于米尔芯驰MYD-JD9X开发板
本篇测评由面包板论坛的优秀测评者“JerryZhen”提供。 本文将介绍基于米尔电子MYD-JD9X开发板打造成开源的Thingsboard网关。 Thingsboard网关是一个开源的软件网关,采用python作为开发语言,可以部署在任何支持 python 运行环境的主机上,灵…...

英语——语法——从句——名词性从句——笔记
文章目录 名词性从句一、定义二、分类(一)宾语从句(二)主语从句(三)C同位语从句(四)D表语从句 名词性从句 一、句子成分 简而言之,构成一个句子的成分(或要素…...

PROSTATEx-2 上前列腺癌的 3D CNN 分类
内容 本文介绍了在多参数 MRI 序列上使用 3D CNN 对前列腺癌进行显着性或不显着性分类。内容如下: 数据集描述Dicom 到 Nifti 文件格式的转换不同 MRI 序列的联合配准...

npm ERR! node-sass@6.0.1 postinstall: `node scripts/build.js`
1.遇到的问题 vue npm install提示以下错误 2.首次尝试方法 尝试用下面的方式重新安装弄得-saas,结果不起作用 。 npm config set sass_binary_sitehttps://npm.taobao.org/mirrors/node-sass npm install node-sass 这时考虑降级node版本,node.js从…...

3D学习论文参考-ACCURATE EYE PUPIL LOCALIZATION USING HETEROGENEOUS CNN MODELS
以下是该文档的关键内容: 该论文提出了一种使用异构卷积神经网络(CNN)模型的精确眼睛瞳孔定位算法。这种算法可以抵抗光照、图像分辨率和眼镜佩戴等干扰条件,同时具有高准确性。该算法由两部分组成:一是找到近似眼睛区…...
迁移conda环境后,非root用户执行pip命令和jupyter命令报错/bad interpreter: Permission denied
移动conda环境,在移动的环境执行pip和jupyter 报错-bash: /data/home/用户名/anaconda3/envs/llm/bin/pip: /root/anaconda3/envs/llm/bin/python: bad interpreter: Permission denied 报错信息 一、原因 原因是当前的这个data/home/用户名/anaconda3/envs/环境名…...
虚拟机使用linux常用问题(虚拟机操作系统:ubuntu 22.04LTS)
1.虚拟机连接外网 ubuntu解决网络连接的解决方案 CentOS7联网问题解决 明明连接好了但是没有网络的情况 2.虚拟机磁盘扩容 相关博客 利用gparted工具时,直接将unallocated空间的前一个位置的磁盘resize,将unallocated的空间全部覆盖 3.虚拟机与本机共享文件 安装vmtools 设…...
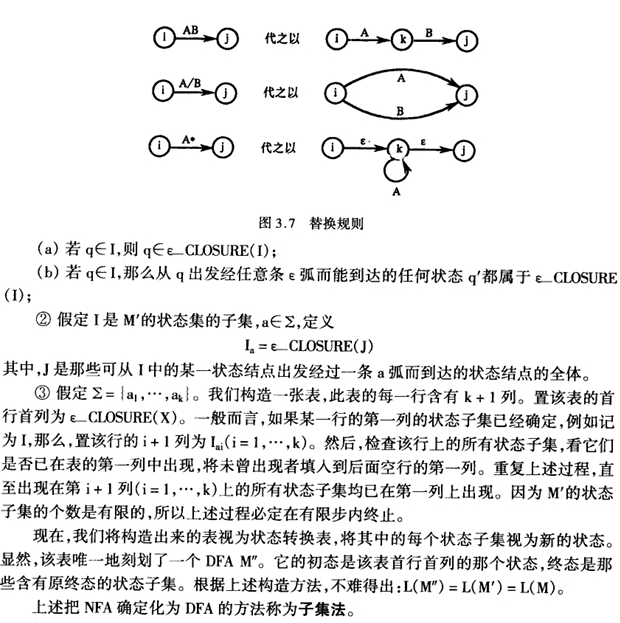
编译原理-词法分析器
文章目录 对于词法分析器的要求概念词法分析器的功能和输出形式 词法分析器的设计词法分析器的结构单词符号的识别:超前搜索状态转换图 正规表达式和有限自动机正规式和正规集确定有限自动机(DFA)非确定有限自动机(NFA)…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...