【每日一题】掷骰子等于目标和的方法数
文章目录
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:动态规划
- 写在最后
Tag
【动态规划】【数组】
题目来源
1155. 掷骰子等于目标和的方法数

题目解读
你手里有 n 个一样的骰子,每个骰子都有 k 个面,分别标号 1 到 n。给定三个整数 n,k 和 target,返回这个 n 个骰子正面朝上的数字组成 target 的所有方案数。答案可能很大,返回对 1 e 9 + 7 1e9+7 1e9+7 取模后的值。
解题思路
方法一:动态规划
我们可以使用动态来解决本题。
状态
记 f[i][j] 表示使用 i 个骰子且数字和为 j 的方案数。
转移关系
我们可以枚举最后一个骰子的数字,数字的范围在 [1, k],使用 i 个骰子组成的数字和为 j 的方案数为:
f [ i , j ] = ∑ x = 1 k f [ i − 1 ] [ j − k ] f\left[ i,j \right] =\sum_{x=1}^k{f\left[ i-1 \right] \left[ j-k \right]} f[i,j]=x=1∑kf[i−1][j−k]
base case
f[0][0] = 1,计即我们还没有掷骰子,数字之和为 0 时的方案数。
最终返回
最终返回 f[n][target],表示使用 n 个骰子正面朝上的数字组成 target 的所有方案数
实现代码
class Solution {
public:int numRollsToTarget(int n, int k, int target) {if (target < n || target > n * k) {return 0;}const int MOD = 1e9 + 7;vector<vector<int>> f(n+1, vector<int>(target+1));f[0][0] = 1;for (int i = 1; i <= n; ++i) {for (int j = 0; j <= target; ++j) {for (int x = 1; x <= k; ++x) {if (j - x >= 0) {f[i][j] = (f[i][j] + f[i-1][j-x]) % MOD;}}}}return f[n][target];}
};
优化
注意观察状态转移方程,f[i][j] 只会从 f[i-1, ...] 转移过来,因此只需要存储第 i 行和第 i-1 行的值,使用两个一维数组代替二维数组进行转态转移。
class Solution {
public:int numRollsToTarget(int n, int k, int target) {if (target < n || target > n * k) {return 0;}const int MOD = 1e9 + 7;vector<int> f(target + 1);f[0] = 1;for (int i = 1; i <= n; ++i) {vector<int> g(target + 1);for (int j = 0; j <= target; ++j) {for (int x = 1; x <= k; ++x) {if (j - x >= 0) {g[j] = (g[j] + f[j-x]) % MOD;}}}f = g;}return f[target];}
};
复杂度分析
时间复杂度: O ( n ⋅ k ⋅ t a r g e t ) O(n \cdot k \cdot target) O(n⋅k⋅target)。
空间复杂度: O ( n ⋅ t r a g e t ) O(n \cdot traget) O(n⋅traget),优化后的空间复杂度为 O ( t a r g e t ) O(target) O(target)。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【每日一题】掷骰子等于目标和的方法数
文章目录 Tag题目来源题目解读解题思路方法一:动态规划 写在最后 Tag 【动态规划】【数组】 题目来源 1155. 掷骰子等于目标和的方法数 题目解读 你手里有 n 个一样的骰子,每个骰子都有 k 个面,分别标号 1 到 n。给定三个整数 n࿰…...

霸王条款惹品牌争议,京东双11站在商家对立面?
作者 | 江北 来源 | 洞见新研社 双11活动第一天,京东就站上了风口浪尖。 与烘焙烤箱品牌海氏的话题接连登上微博热搜,海氏控诉京东滥用市场竞争地位,破坏市场竞争秩序。在海氏的声明中,京东的行为让吃瓜群众大开眼界:…...

深度神经网络为何成功?其中的过程、思想和关键主张选择
LeNet(1989)在小数据集上取得了很好的效果,但是在更大、更真实地数据集上训练卷积神经网络地性能和可行性还有待研究。 与神经网络竞争的是传统机器学习方法,比如SVM(支持向量机)。这个阶段性能比神经网络方…...

什么是服务器节点?
一.服务器节点的概念: 服务器节点是一种服务器装置,节点服务器是针对服务器集群来说的。主要应用在WEB、FTP等等的服务上。所以节点服务器并不是单指某一种服务器。它由多个节点和管理装置整体的管理单元构成,其特征在于:各节点具…...

水电站与数据可视化:洞察未来能源趋势的窗口
在信息时代的浪潮中,数据可视化正成为推动能源领域发展的重要工具。今天,我们将带您一起探索水电站与数据可视化的结合,如何成为洞察未来能源趋势的窗口。水电站作为传统能源领域的重要组成部分,它的运行与管理涉及大量的数据。然…...
Mac运行Docker报错
Mac运行Docker报错 📔 千寻简笔记介绍 千寻简笔记已开源,Gitee与GitHub搜索chihiro-notes,包含笔记源文件.md,以及PDF版本方便阅读,且是用了精美主题,阅读体验更佳,如果文章对你有帮助请帮我点…...
.click(function(){ 和代码 $(document).ready(function() 有啥区别?)
代码 $(“.btn“).click(function(){ 和代码 $(document).ready(function() 有啥区别?
看下面的内容前可以先看下博文:https://blog.csdn.net/wenhao_ir/article/details/134029389 $(".btn").click(function(){...}) 和 $(document).ready(function(){...}) 是两种不同的 jQuery 事件处理方式,它们有不同的用途和时机࿱…...

【nodejs脚本】为文件夹中的所有node项目执行命令 npm install 并收集error日志
目录 im 下有很多的node项目,我需要批量为这些项目执行 npm install,另外npm的error信息需要单独收集至log文件中 var fs require(fs); var util require(util); var exec util.promisify(require(child_process).exec);var projectsDirectory .; v…...

非父子组件通信-发布订阅模式
发布订阅模式其实与vue无关,完全是ES6的代码,但是它可以通过这种模式实现非父子组件的通信 store.js文件 首先创建一个store.js文件,用于提供发布与订阅方法 export default {datalist: [], //存放带一个参数的函数集合//订阅subscribe(fu…...

iPhone手机分辨率整理
手机机型(iPhone)屏幕尺寸 (inch)逻辑分辨率(pt)设备分辨率(px)缩放因子(Scale Factor)竖屏安全区域(safeAreaInsets)纵横比(Aspect ratio)像素密度(ppi)2G/3G/3GS3.5320*480320*4801xtop:20 bottom:03:21654/4(s)3.5320*480640*9602xtop:20 bottom:016:…...
【linux】SourceForge 开源软件开发平台和仓库
在linux上面安装服务和工具。我们经常会下载安装包。今天推荐一个网站。 SourceForge 开源软件开发平台和仓库 全球最大开源软件开发平台和仓库 SourceForge.net,又称SF.net,是开源软件开发者进行开发管理的集中式场所。 SourceForge.net由VA Softwa…...
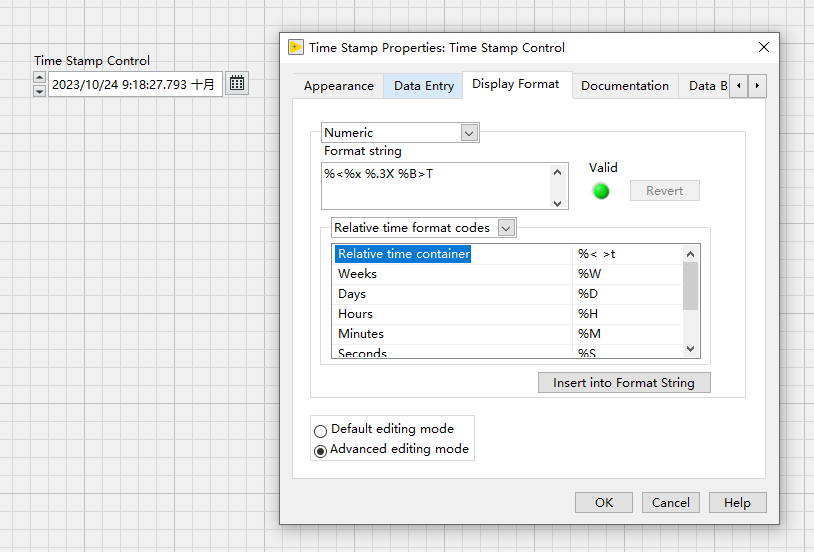
LabVIEW应用开发——控件的使用(四)
接上文,这篇介绍时间控件。 LabVIEW应用开发——控件的使用(三) 1、时间控件Time Stamp control 在日常软件开发场景中,时间也是一种常用的控件,用于表达当前时间的显示、对下设置时间、时间同步等等场景。LabVIEW专门…...

MySQL - mvcc
mvcc 是什么? MVCC(多版本并发控制)是一种数据库并发控制机制,旨在提高数据库的并发性,避免锁定操作,从而减少等待和提高性能。MVCC 主要解决数据库读写操作之间的线程安全问题。 MVCC 主要有两种读取数据…...

SpringMVC 异常处理器
1、基于配置的异常处理 SpringMVC提供了一个处理控制器方法执行过程中所出现的异常的接口:HandlerExceptionResolver HandlerExceptionResolver接口的实现类有:DefaultHandlerExceptionResolver和SimpleMappingExceptionResolver SpringMVC提供了自定…...

迷你洗衣机哪个牌子好又实惠?内裤洗衣机热销前四榜单
小型内裤洗衣机是一款很实用的家用电器,非常适合住在小户型的房子里,或者经常要出差的人。所以,买什么牌子的内衣洗衣机比较好?目前市场上各品牌各有各的特色及应用场合,例如适合于贴身衣物如内衣、内裤、婴儿衣物清洗…...

SOCKS5代理与网络安全:如何安全地进行爬虫操作
随着网络技术的不断发展,代理技术在网络安全和数据爬取中扮演着越来越重要的角色。本文将重点介绍SOCKS5代理、SK5代理和IP代理的基本概念,以及如何在保证网络安全的前提下,利用这些技术进行有效的爬虫操作。 1. SOCKS5代理与SK5代理 SOCKS…...

onebound电商API接口商品数据采集平台:让数据成为生产力!
随着数字化商业时代的到来,API接口已成为电商资源连接利器,也是全球传统互联网企业转型的基础。 2021年 Google Cloud 研究显示,全球互联网企业近3/4的企业持续投入数字化转型,2/3的企业在持续增加投入,从这组数据可以…...

Kafka磁盘写满日志清理操作
最近项目组的kafka集群,老是由于应用端写入kafka topic的消息太多,导致所在的broker节点占满,导致其他的组件接连宕机。 这里和应用端沟通可以删除1天之前的消息来清理磁盘,并且可以调整topic的消息存活时间。 一、调整Topic的消…...

SSL证书:网络通信安全的基石
随着互联网的深入发展和电子商务的普及,网络安全问题变得越来越重要。SSL证书作为保障网络通信安全的重要组成部分,扮演着至关重要的角色。本文将深入剖析SSL证书的底层原理、作用、应用场景以及优缺点,帮助您更好地理解网络通信安全。 一、…...

Python第三方库 - Flash(python web框架)
1 Flask 1.1 认识Flask Web Application Framework( Web 应用程序框架)或简单的 Web Framework( Web 框架)表示一个库和模块的集合,使 Web 应用程序开发人员能够编写应用程序,而不必担心协议,线…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...
运行vue项目报错 errors and 0 warnings potentially fixable with the `--fix` option.
报错 找到package.json文件 找到这个修改成 "lint": "eslint --fix --ext .js,.vue src" 为elsint有配置结尾换行符,最后运行:npm run lint --fix...

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解
在我的上一篇博客:基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目,该项目展示了一个强大的框架,旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人,更是一个集…...
