【算法刷题】动态规划算法题型及方法归纳
动态规划特点
动态规划中每一个状态一定是由上一个状态推导出来,根据这个特点,可以在状态计算过程中,存储某一条件下的数据,当再次遍历该条件时,直接取该条件对应的数据即可,可以避免重复计算,减少时间。
解题步骤:动态规划五步曲
(1)确定dp数组(dp table)以及下标的含义
(2)确定递推公式
(3)dp数组如何初始化
(4)确定遍历顺序
(5)举例推导dp数组
1、动态规划基础题
- dp[i] = dp[i - 1] + dp[i - 2]
144、【动态规划】leetcode ——509. 斐波那契数:递归法+迭代法(C++版本):优化方法是让dp[1]始终指向最后,dp[0]指向前一位,用sum作为中间临时变量
爬楼梯(两道):
-
dp[i] = dp[i - 1] + dp[i - 2]
145、【动态规划】leetcode ——70. 爬楼梯:暴力法+动态规划(C++版本):爬到第i阶楼梯可以依托于爬第i - 1阶楼梯的方式,或依托于爬到第i - 2阶楼梯的方式。 -
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i -2])
146、【动态规划】leetcode ——746. 使用最小花费爬楼梯:递归法+迭代法(C++版本):注意分清到第i层并不花费第i层的费用,只有跳到第i + 1层或第i + 2层才花费。找到跳到该层之前的最小费用方案。
机器人运动路径(两道):
-
dp[i][j] = d[i - 1][j] + dp[i][j - 1]
147、【动态规划】leetcode ——62. 不同路径:递归法+迭代法(C++版本):到达i,j可以从i-1,j或i,j-1两个位置到达,依托于这两个位置上的可到达路径,再加上这条路径到达i,j。 -
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
148、【动态规划】leetcode ——63. 不同路径 II:递归法+迭代法(C++版本):与上面的相比,多一个条件判定,只统计没有障碍物的位置,对于到达有障碍物的位置,不统计。
拆分数字:
-
dp[i] = max(d[i], max(j * (i - j), j * dp[i - j]))
149、【动态规划】leetcode ——343. 整数拆分(C++版本):d[i[表示数字i,拆分后可得到的乘积最大值,找到分成两个j * (i - j)和分成三个及以上j * dp[i - j]中的最大值,再和之前已得到的dp[i]相比,求出当前乘积最大值。 -
dp[i] += dp[j - 1] * dp[i - j]
150、【动态规划】leetcode ——96. 不同的二叉搜索树(C++版本):以i为根节点,构造的BST个数 = 以j - 1为根节点的个数 * 以i - j为根节点的个数,再让j从0到i的各种情况求和。
2、背包问题
背包问题是在规定背包容量为j的前提下,每个物品对应的体积为v[i],价值为w[i],从物品0到物品i中选择物品放入背包中,找出符合某种要求的价值。
(1)背包问题种类
- 01背包:每种物品只能选择1个。
- 完全背包:每种物品可以选择无限个。
- 多重背包:每种物品最多可选s[i]个。
(2)递推公式
- 01背包:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]) - 完全背包:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]) - 多重背包:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i], dp[i - 1][j - 2*v[i]] + w[i] + ... + dp[i - 1][j - s[i]*v[i]] + s[i]*w[i])
(3)滚动数组遍历顺序:
- 01背包:从大到小
- 完全背包:从小到大
- 多重背包:在01背包的基础上,从大到小,多一层for循环选物品个数
详细内容:【动态规划】背包问题题型及方法归纳
3、打家劫舍问题
-
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
163、【动态规划】leetcode ——198. 打家劫舍(C++版本):不选当前而选择前一个i-1物品,选择当前物品i之间找最大值。 -
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])+分别对两个范围的数组进行dp更新求最大值
163、【动态规划】leetcode ——213. 打家劫舍 II:环形列表线性化(C++版本):将环形列表线性化,分成两种情况,求二者中的最大值。 -
树形dp,max(偷当前结点, 不偷当前结点)
165、【动态规划】leetcode ——337. 打家劫舍 III:记忆化递归+动态规划(C++版本):树形dp需采用后序遍历,每次返回值为一个二维数组(0:不偷,1:偷),分别遍历左和右子树,然后将偷当前结点的结果与不偷当前结点的结果对比,取二者中的最大值。
4、股票问题
(1)仅能进行一次和无限次的买卖股票
设置两个dp,dp[i][0]表示持有股票时,具有的最大收益;dp[i][1]表示不持有股票时,具有的最大收益。
模板:
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n + 1, vector<int>(2));dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1; i < n; i++) {// 仅能进行一次买卖操作:// dp[i][0] = max(dp[i - 1][0], - prices[i]);// 可以进行多次买卖操作:dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[n - 1][1];}
};-
持有:dp[i][0] = max(dp[i-1][0], -prices[i])、不持有:dp[i][1] = max(dp[i-1], dp[i][0] + prices[i])
168、【贪心算法】leetcode ——121. 买卖股票的最佳时机:dp数组+变量优化 (C++版本):仅允许进行一次买卖 -
持有:dp[i][0] = max(dp[i-1][0], dp[i][1] - prices[i])、不持有:dp[i][1] = max(dp[i-1], dp[i][0] + prices[i])
130、【贪心算法/动态规划】leetcode ——122. 买卖股票的最佳时机 II(贪心算法)(C++版本):可以进行多次买卖 -
持有:dp[i][0] = max(dp[i-1][0], dp[i][1] - prices[i])、不持有:dp[i][1] = max(dp[i-1], dp[i][0] + prices[i] - fee)
172、【动态规划】leetcode ——714. 买卖股票的最佳时机含手续费 (C++版本):相比于2多了一个扣除手续费。
(2)可以进行有限次的买卖股票
模板:
class Solution {
public:int maxProfit(int k, vector<int>& prices) {if(prices.empty() || prices.size() == 1) return 0;int n = prices.size();vector<vector<int>> dp(n + 1, vector<int>(2 * k + 1));// dp[0][0] = 0for(int i = 1; i < 2 * k + 1; i += 2) {dp[0][i] = -prices[0]; // 2*k-1为持有为-prices[0],2*k为不持有为0。}for(int i = 1; i < n; i++) {for(int j = 1; j < 2 * k + 1; j += 2) {dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] - prices[i]);dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] + prices[i]);}}return dp[n - 1][2 * k];}
};-
第一次持有:dp[i][1] = max(dp[i - 1][1], -prices[i]),第一次不持有:dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]),第二次持有:dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]), 第二次不持有:dp[i][4] = max(dp[i - 1][4], dp[i-1][3] + prices[i])
169、【贪心算法】leetcode ——123. 买卖股票的最佳时机 III:二维数组+一维数组 (C++版本):可以进行两次买卖 -
第k次持有:dp[i][2 * k - 1] = max(dp[i - 1][2 * k - 1], dp[i - 1][2 * k - 2] - prices[i]),第k次不持有:dp[i][2 * k] = max(dp[i - 1][2 * k], dp[i - 1][2 * k - 1] + prices[i])
170、【贪心算法】leetcode ——188. 买卖股票的最佳时机 IV:二维数组+一维数组 (C++版本):可以进行k次买卖
(3)含有冷冻期,可以进行有限次的买卖股票
- 持有股票:dp[i][0] = max(dp[i - 1][0], dp[i - 1][2] - prices[i])、不持有股票且明天将为冷冻期:dp[i][1] = dp[i][0] + prices[i]、不持有股票且明天不为冷冻期:dp[i][2] = max(dp[i - 1][2], dp[i - 1][1])
171、【动态规划】leetcode ——309. 最佳买卖股票时机含冷冻期 (C++版本)
5、子序列问题
(1)递增子序列问题
-
dp[i] = max(dp[i], dp[j]+1)
173、【动态规划】leetcode ——300. 最长递增子序列 (C++版本):按顺序遍历,当对比发现当前元素大于前方某一位置元素时,就在该位置元素已有的最长递增子序列长度上加一和当前元素已记录的最长递增子序列长度对比,最大值。 -
dp[i] = dp[i -1] + 1
174、【动态规划/贪心算法】leetcode ——674. 最长连续递增序列 (C++版本):每遇到一个连续递增子序列,就在前一个的基础上加一。
(2)编辑距离
-
dp[i][j] = dp[i - 1][j - 1] + 1
175、【动态规划】leetcode ——718. 最长重复子数组 (C++版本):比较到nums1[i -1]与nums2[j - 1]相等时,在前一个的基础上加一。 -
当
text1[i - 1] == text2[j - 1]时,令dp[i][j] == dp[i - 1][j - 1] + 1;当不等于时,dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])
176、【动态规划】leetcode ——1143. 最长公共子序列(C++版本):与1的区别在于,2中不要求子序列连续。
拓展题: 177、【动态规划】leetcode ——1143. 最长公共子序列(C++版本):注意问题转化。 -
dp[i] = max(dp[i] + nums[i], nums[i])
129、【动态规划/贪心算法】leetcode ——53. 最大子数组和(C++版本):当前的加上之前的和从当前情况重新开始,二者之间取最大值。 -
当
text1[i - 1] == text2[j - 1]时,令dp[i][j] == dp[i - 1][j - 1] + 1;当不等于时,dp[i][j] = dp[i][j - 1]
178、【数组/动态规划】leetcode ——392. 判断子序列:双指针+动态规划(C++版本):思路与(2)的区别在于遇到不等时,固定子串,整体串前移一个 -
当
s[i - 1] == t[j - 1]时,令dp[i][j] == dp[i - 1][j - 1] + dp[i-1]dp[j];当不等于时,dp[i][j] = dp[i][j - 1]
178、【动态规划】leetcode ——115. 不同的子序列(C++版本):与(5)中不同的在于此时要进行累计,因此需要再加上t维持不动s缩一个的情况。 -
思路一:当
word1[i - 1] == word2[j - 1]时,令dp[i][j] == dp[i - 1][j - 1];当不等于时,dp[i][j] = min(dp[i][j - 1] + 1, dp[i - 1][j] + 1)
思路二:在求最长公共子序列的基础上,得到长度,也能搞两个序列总长度减去二倍的最长公共子序列长度。
180、【动态规划】leetcode ——583. 两个字符串的删除操作:两种动态规划思路(C++版本) -
相等:
dp[i][j] = dp[i - 1][j - 1],不相等:1)增:dp[i][j - 1] + 1;2)删:dp[i - 1][j] + 1;3)改:dp[i - 1][j - 1] + 1
181、【动态规划】leetcode ——72. 编辑距离(C++版本):主要是两个状态四个操作,相等时对应状态一种操作,不相等时对应状态三种操作。
(3)回文串
-
当
s[i]==s[j]时,若j - i <= 1,则dp[i][j]=true;若j - i > 1且dp[i-1][j+1]==true,则dp[i][j]=true,否则为false。当s[i]!=s[j]时,则dp[i][j]=false
182、【动态规划/数组】leetcode ——647. 回文子串:动态规划+双指针(C++版本):每次判定两段,然后基于长度情况和上一次结果的进行判定。 -
当
s[i]==s[j]时,dp[i][j]=dp[i+1][j-1]+2;当s[i]!=s[j]时,dp[i][j]=max(dp[i][j-1],dp[i+1][j])。
182、【动态规划】leetcode ——516. 最长回文子序列(C++版本)
相关文章:

【算法刷题】动态规划算法题型及方法归纳
动态规划特点 动态规划中每一个状态一定是由上一个状态推导出来,根据这个特点,可以在状态计算过程中,存储某一条件下的数据,当再次遍历该条件时,直接取该条件对应的数据即可,可以避免重复计算,…...

PolarDB数据库的CSN机制
背景 对postgres数据库熟悉的同学会发现在高并发场景下在获取快照处易出现性能瓶颈,其原因在于PG使用全局数组在共享内存中保存所有事务的状态,在获取快照时需要加锁以保证数据一致性。获取快照时需要持有ProcArraryLock共享锁比遍历ProcArray数组中活跃…...

使用kubeadm 部署kubernetes 1.26.1集群 Calico ToR配置
目录 机器信息 升级内核 系统配置 部署容器运行时Containerd 安装crictl客户端命令 配置服务器支持开启ipvs的前提条件 安装 kubeadm、kubelet 和 kubectl 初始化集群 (master) 安装CNI Calico 集群加入node节点 机器信息 主机名集群角色IP内…...
Servlet笔记(11):Servletcontext对象
1、什么是ServletContext ServletContext是一个全局储存空间,随服务器的生命周期变化, Cookie,Session,ServletContext的区别 Cookie: 存在于客户端的本地文本文件 Session: 存在于服务器的文本文件&#…...

EM算法是什么
EM算法是什么 EM算法(Expectation-Maximization Algorithm)是一种用于参数估计的迭代算法。它常被用于含有隐变量(latent variable)的概率模型中,例如高斯混合模型、隐马尔可夫模型等。 EM算法分为两个步骤ÿ…...

C++---线性dp---方格取数(每日一道算法2023.2.25)
注意事项: 本题属于"数字三角形"和"摘花生"两题的进阶版,建议优先看懂那两道,有助理解。 题目: 输入: 8 2 3 13 2 6 6 3 5 7 4 4 14 5 2 21 5 6 4 6 3 15 7 2 14 0 0 0输出: 67#include <cm…...
《第一行代码》 第八章:应用手机多媒体
一,使用通知 第一步,创建项目,书写布局 <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"android:orientation"vertical"android:layout_width"match_parent"android:layout_he…...

C++设计模式(20)——迭代器模式
亦称: Iterator 意图 迭代器模式是一种行为设计模式, 让你能在不暴露集合底层表现形式 (列表、 栈和树等) 的情况下遍历集合中所有的元素。 问题 集合是编程中最常使用的数据类型之一。 尽管如此, 集合只是一组对…...
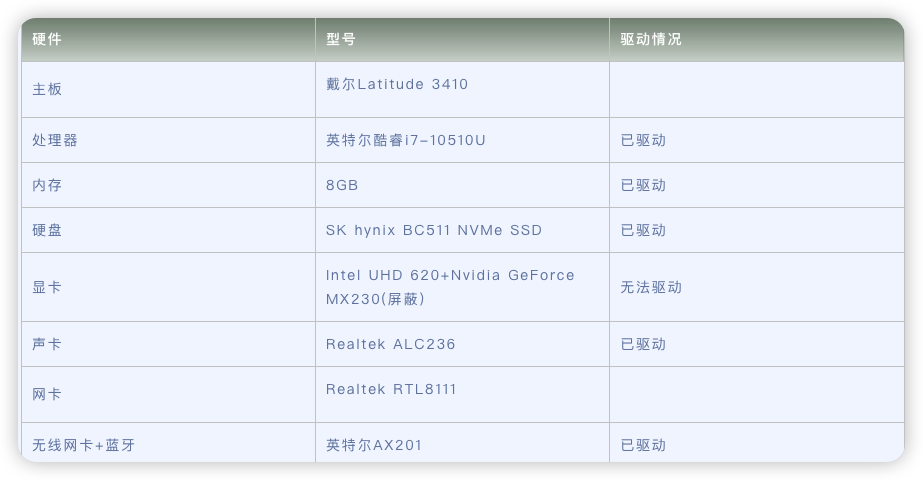
戴尔Latitude 3410电脑 Hackintosh 黑苹果efi引导文件
原文来源于黑果魏叔官网,转载需注明出处。硬件型号驱动情况主板戴尔Latitude 3410处理器英特尔酷睿i7-10510U已驱动内存8GB已驱动硬盘SK hynix BC511 NVMe SSD已驱动显卡Intel UHD 620Nvidia GeForce MX230(屏蔽)无法驱动声卡Realtek ALC236已驱动网卡Realtek RTL81…...
)
一起Talk Android吧(第五百零四回:如何调整组件在约束布局中的位置)
文章目录 背景介绍调整方法一调整方法二经验分享各位看官们大家好,上一回中咱们说的例子是"解决retrofit被混淆后代码出错的问题",这一回中咱们说的例子是" 如何调整组件在约束布局中的位置"。闲话休提,言归正转, 让我们一起Talk Android吧! 背景介绍…...
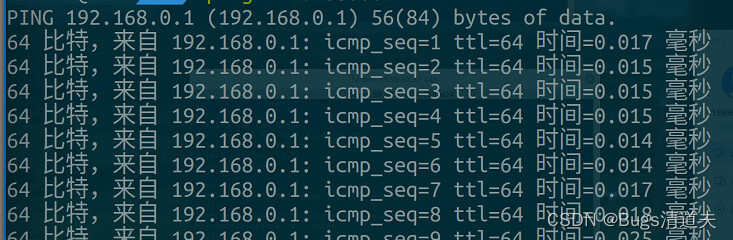
ssh连不上实验室的物理机了
实验室的电脑,不能在校外用 ssh 连接了 192.168.1.33 是本地地址,掩码16位,图1。 192.168.1.14 是实验室的另一台可以ssh连接的物理机,掩码16。 192.168.0.1 是无线路由器地址。 192.168.0.2 是192.168.1.14上的虚拟机地址&#…...

selinux讲解
Selinux讲解 1、selinux的概述 Selinux的历史 Linux安全性与windows在不开启防御措施的时候是一样的;同样是C2级别的安全防护安全级别评定: D–>C1–>C2–>B1–>B2–>B3–>A1 D级,最低安全性C1级,主存取控制…...
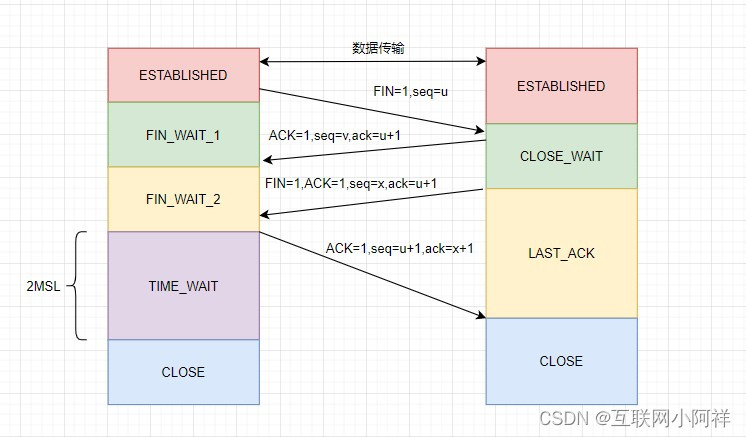
【计算机网络】TCP底层设计交互原理
文章目录1.TCP底层三次握手详细流程2.TCP洪水攻击介绍和ss命令浅析3.Linux服务器TCP洪水攻击入侵案例4.TCP洪水攻击结果分析和解决方案5.TCP底层四次挥手详细流程1.TCP底层三次握手详细流程 TCP的可靠性传输机制:TCP三次我手的流程 一次握手:客户端发送一…...

Kotlin1.8新特性
Kotlin1.8.0新特性 新特性概述 JVM 的新实验性功能:递归复制或删除目录内容提升了 kotlin-reflect 性能新的 -Xdebug 编译器选项,提供更出色的调试体验kotlin-stdlib-jdk7 与 kotlin-stdlib-jdk8 合并为 kotlin-stdlib提升了 Objective-C/Swift 互操作…...
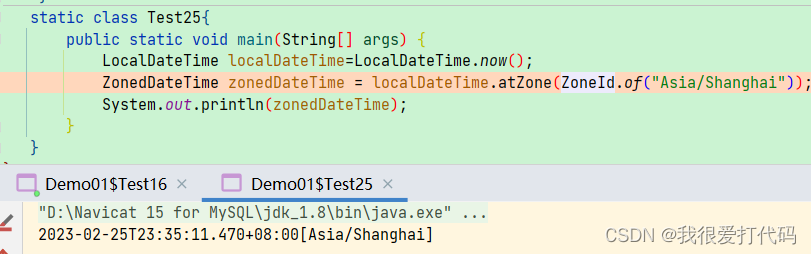
【Java8】
1、接口中默认方法修饰为普通方法 在jdk8之前,interface之中可以定义变量和方法,变量必须是public、static、final的,方法必须是public、abstract的,由于这些修饰符都是默认的。 接口定义方法: public抽象方法需要子类实现 接口定…...

阿里 Java 程序员面试经验分享,附带个人学习笔记、路线大纲
背景经历 当时我工作近5年,明显感觉到了瓶颈期。说句不好听的成了老油条,可以每天舒服的混日子(这也有好处,有时间准备面试)。这对于个人成长不利,长此以往可能面临大龄失业。所以我觉得需要痛下决心改变一…...
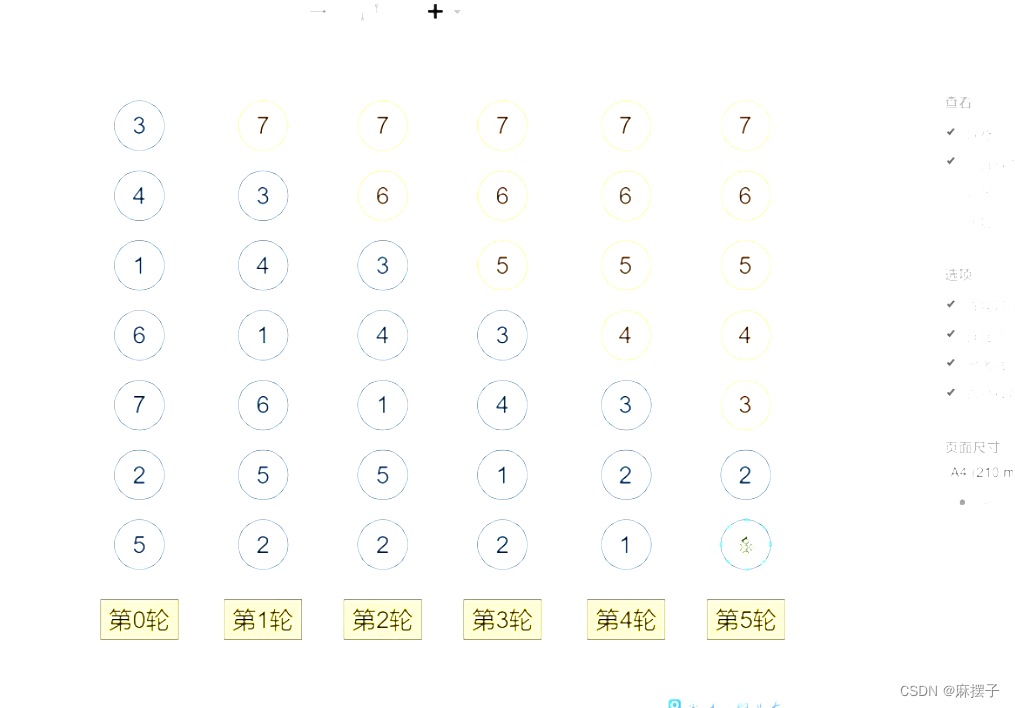
十大算法基础——上(共有20道例题,大多数为简单题)
一、枚举(Enumerate)算法 定义:就是一个个举例出来,然后看看符不符合条件。 举例:一个数组中的数互不相同,求其中和为0的数对的个数。 for (int i 0; i < n; i)for (int j 0; j < i; j)if (a[i] …...
)
【PAT甲级题解记录】1018 Public Bike Management (30 分)
【PAT甲级题解记录】1018 Public Bike Management (30 分) 前言 Problem:1018 Public Bike Management (30 分) Tags:dijkstra最短路径 DFS Difficulty:剧情模式 想流点汗 想流点血 死而无憾 Address:1018 Public Bike Managemen…...
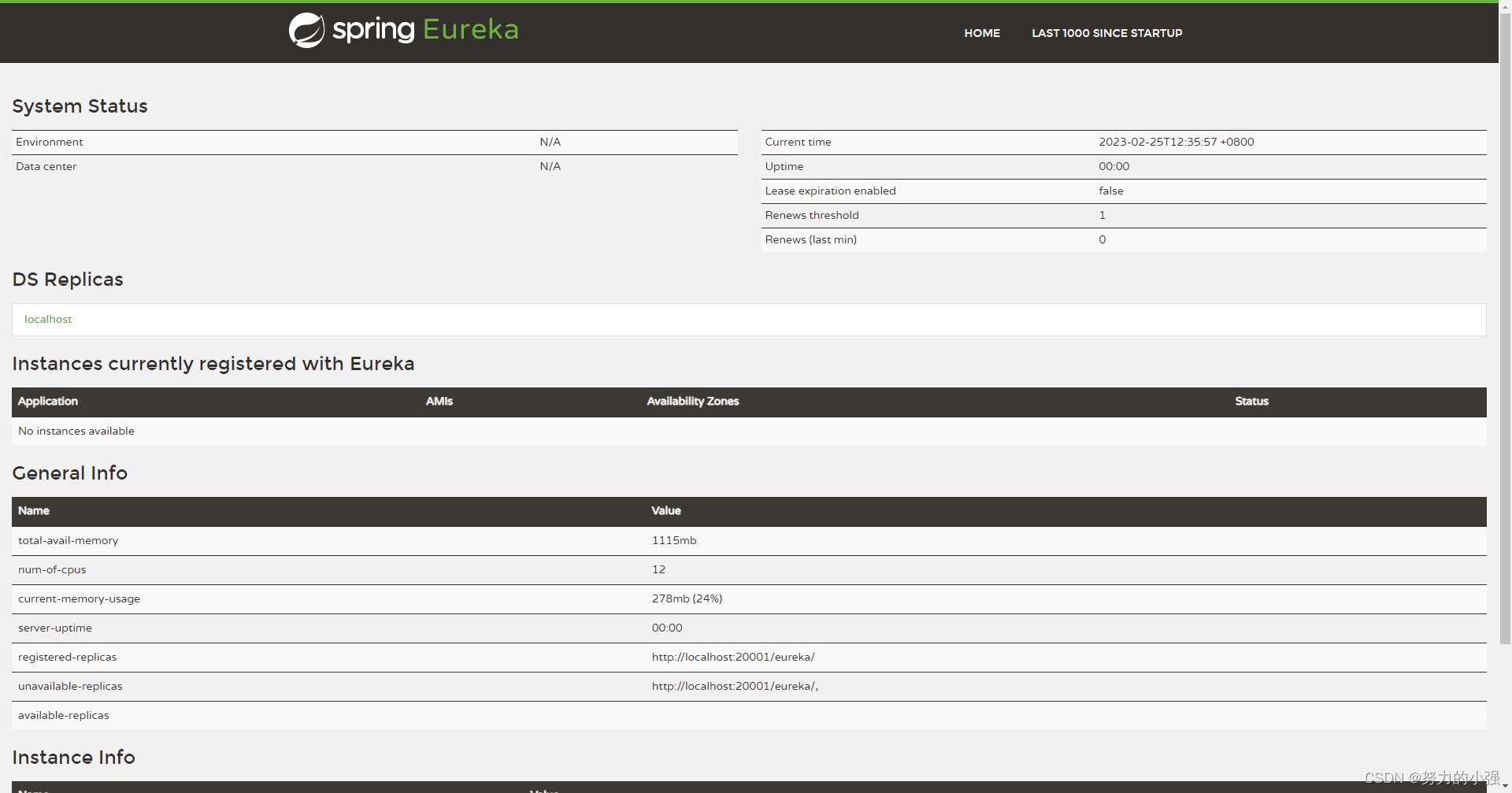
SpringCloud————Eureka概述及单机注册中心搭建
Spring Cloud Eureka是Netflix开发的注册发现组件,本身是一个基于REST的服务。提供注册与发现,同时还提供了负载均衡、故障转移等能力。 Eureka组件的三个角色 服务中心服务提供者服务消费者 Eureka Server:服务器端。提供服务的注册和发现…...
 分页)
原生django raw() 分页
def change_obj_to_dict(self,temp):dict {}dict["wxh_name"] temp.wxh_namedict["types"] temp.typesdict["subject"] temp.subjectdict["ids"] temp.ids# 虽然产品表里没有替代型号,但是通过sql语句的raw()查询可以…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
