C++---线性dp---方格取数(每日一道算法2023.2.25)
注意事项:
本题属于"数字三角形"和"摘花生"两题的进阶版,建议优先看懂那两道,有助理解。
题目:

输入:
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出:
67
#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;int const N = 11;
int w[N][N], f[N+N][N][N]; //注意k要开两倍,因为是i+j的总和
int n;int main()
{cin >> n;//接收数据直到“0 0 0”为止int a, b, c;while (cin >> a >> b >> c, a || b || c) w[a][b] = c;//线性dpfor (int k = 2; k<=n+n; k++) {for (int i1 = 1; i1<=n; i1++) {for (int i2 = 1; i2<=n; i2++) {// k = i1+j1 = i2+j2, 切记是相等关系int j1 = k-i1, j2 = k-i2;if (j1 >= 1 && j2 >= 1 && j1 <= n && j2 <= n) { //判断j1和j2的合法性//如果是重叠点就只加一次,例如(1,2)(1,2), 如果是非重叠点就将两个点都加上,例如(1, 2)(2, 1)int t = w[i1][j1];if (i1 != i2) t += w[i2][j2];//引用节省代码量,分四种情况讨论上两个点如何进行移动int &x = f[k][i1][i2];x = max(x, f[k-1][i1-1][i2-1]); //down,downx = max(x, f[k-1][i1-1][i2
); //down,rightx = max(x, f[k-1][i1][i2-1]); //right,downx = max(x, f[k-1][i1][i2]); //right, rightx += t;}}}}cout << f[n+n][n][n];return 0;
}
思路:
这道题的难点在于如何将每次一个点的线性dp转变为同时计算两个点
1:将单一点的线性dp跑两次,计算的时候将走过的点进行标注,权重变为0即可。
2:找到点与点的关系,同时计算两个点的dp。
这里我们讲第二种
还是熟悉的y式dp法。
1.状态表示:
f[k][i1][i2]: 从(1, 1)走到(i1, j1) 和 从(1, 1)走到(i2, j2)的最优方案的总和,并且两条线的重复点只能计算一次,属性为Max。
这里的k是表示当 (i1, j1) 和 (i2, j2) 的横纵坐标和 相同时的值。
也就是k = i1+j1 = i2+j2, 因为这样的话,通过k,i1,i2可以推导出j1,j2的值,通过一个量来保存两个量。
这样就很巧妙的解决了标记已使用点的问题,如果两条线走到了相同点,
也就是当i1 = i2, j1 = j2(j1 = k-i1, j2 = k-i2),说明它们在相同点上那么这个点就只计算一次即可,因为数只能取一次。
而当i1 != i2说明状态转移后不在同一个点,那么分别计算w(i1,j1),w(i2,j2)两次。
2.状态计算:
两个点的前一个点向分别向右或下转移,所以有四种情况来讨论:
f[k-1][i1-1][i2-1] + t down,downf[k-1][i1-1][i2] + t down,rightf[k-1][i1][i2-1] + t right,downf[k-1][i1][i2] + t right,right
也就是:f[k][i1][i2] = max(dd, dr, rd, rr)
声明:
算法思路来源为y总,详细请见https://www.acwing.com/
本文仅用作学习记录和交流
ps:最近要开学啦,恢复更新(假期的我真是懒狗…
相关文章:

C++---线性dp---方格取数(每日一道算法2023.2.25)
注意事项: 本题属于"数字三角形"和"摘花生"两题的进阶版,建议优先看懂那两道,有助理解。 题目: 输入: 8 2 3 13 2 6 6 3 5 7 4 4 14 5 2 21 5 6 4 6 3 15 7 2 14 0 0 0输出: 67#include <cm…...
《第一行代码》 第八章:应用手机多媒体
一,使用通知 第一步,创建项目,书写布局 <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"android:orientation"vertical"android:layout_width"match_parent"android:layout_he…...

C++设计模式(20)——迭代器模式
亦称: Iterator 意图 迭代器模式是一种行为设计模式, 让你能在不暴露集合底层表现形式 (列表、 栈和树等) 的情况下遍历集合中所有的元素。 问题 集合是编程中最常使用的数据类型之一。 尽管如此, 集合只是一组对…...
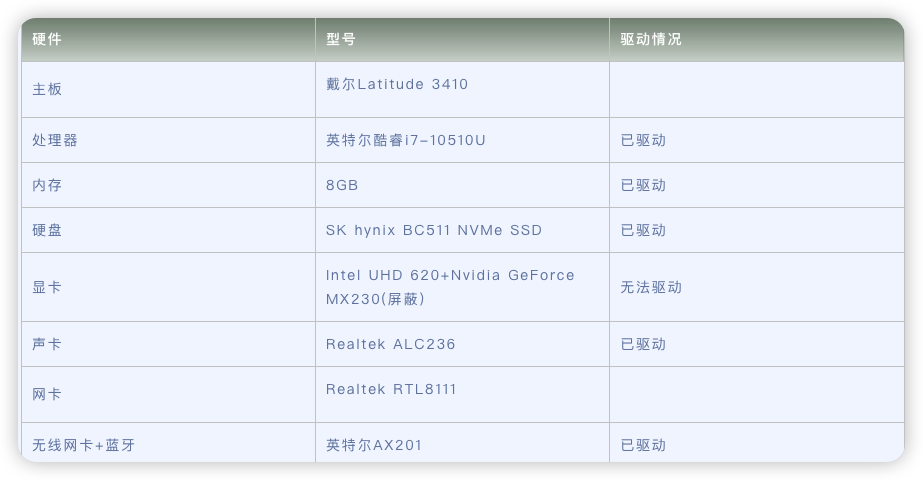
戴尔Latitude 3410电脑 Hackintosh 黑苹果efi引导文件
原文来源于黑果魏叔官网,转载需注明出处。硬件型号驱动情况主板戴尔Latitude 3410处理器英特尔酷睿i7-10510U已驱动内存8GB已驱动硬盘SK hynix BC511 NVMe SSD已驱动显卡Intel UHD 620Nvidia GeForce MX230(屏蔽)无法驱动声卡Realtek ALC236已驱动网卡Realtek RTL81…...
)
一起Talk Android吧(第五百零四回:如何调整组件在约束布局中的位置)
文章目录 背景介绍调整方法一调整方法二经验分享各位看官们大家好,上一回中咱们说的例子是"解决retrofit被混淆后代码出错的问题",这一回中咱们说的例子是" 如何调整组件在约束布局中的位置"。闲话休提,言归正转, 让我们一起Talk Android吧! 背景介绍…...
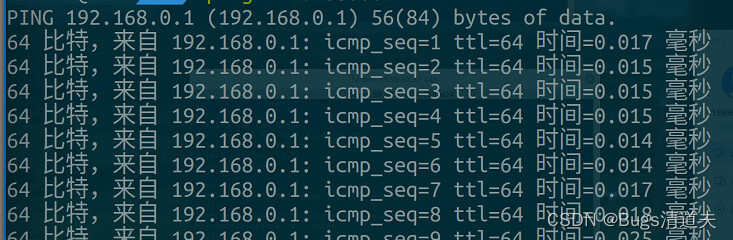
ssh连不上实验室的物理机了
实验室的电脑,不能在校外用 ssh 连接了 192.168.1.33 是本地地址,掩码16位,图1。 192.168.1.14 是实验室的另一台可以ssh连接的物理机,掩码16。 192.168.0.1 是无线路由器地址。 192.168.0.2 是192.168.1.14上的虚拟机地址&#…...

selinux讲解
Selinux讲解 1、selinux的概述 Selinux的历史 Linux安全性与windows在不开启防御措施的时候是一样的;同样是C2级别的安全防护安全级别评定: D–>C1–>C2–>B1–>B2–>B3–>A1 D级,最低安全性C1级,主存取控制…...
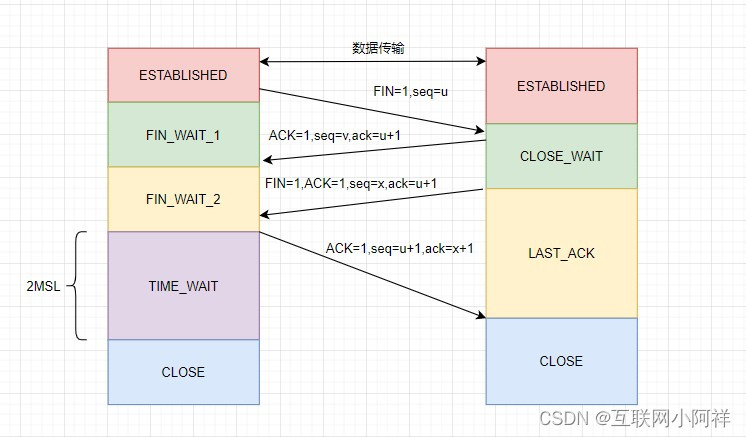
【计算机网络】TCP底层设计交互原理
文章目录1.TCP底层三次握手详细流程2.TCP洪水攻击介绍和ss命令浅析3.Linux服务器TCP洪水攻击入侵案例4.TCP洪水攻击结果分析和解决方案5.TCP底层四次挥手详细流程1.TCP底层三次握手详细流程 TCP的可靠性传输机制:TCP三次我手的流程 一次握手:客户端发送一…...

Kotlin1.8新特性
Kotlin1.8.0新特性 新特性概述 JVM 的新实验性功能:递归复制或删除目录内容提升了 kotlin-reflect 性能新的 -Xdebug 编译器选项,提供更出色的调试体验kotlin-stdlib-jdk7 与 kotlin-stdlib-jdk8 合并为 kotlin-stdlib提升了 Objective-C/Swift 互操作…...
【Java8】
1、接口中默认方法修饰为普通方法 在jdk8之前,interface之中可以定义变量和方法,变量必须是public、static、final的,方法必须是public、abstract的,由于这些修饰符都是默认的。 接口定义方法: public抽象方法需要子类实现 接口定…...

阿里 Java 程序员面试经验分享,附带个人学习笔记、路线大纲
背景经历 当时我工作近5年,明显感觉到了瓶颈期。说句不好听的成了老油条,可以每天舒服的混日子(这也有好处,有时间准备面试)。这对于个人成长不利,长此以往可能面临大龄失业。所以我觉得需要痛下决心改变一…...
十大算法基础——上(共有20道例题,大多数为简单题)
一、枚举(Enumerate)算法 定义:就是一个个举例出来,然后看看符不符合条件。 举例:一个数组中的数互不相同,求其中和为0的数对的个数。 for (int i 0; i < n; i)for (int j 0; j < i; j)if (a[i] …...
)
【PAT甲级题解记录】1018 Public Bike Management (30 分)
【PAT甲级题解记录】1018 Public Bike Management (30 分) 前言 Problem:1018 Public Bike Management (30 分) Tags:dijkstra最短路径 DFS Difficulty:剧情模式 想流点汗 想流点血 死而无憾 Address:1018 Public Bike Managemen…...
SpringCloud————Eureka概述及单机注册中心搭建
Spring Cloud Eureka是Netflix开发的注册发现组件,本身是一个基于REST的服务。提供注册与发现,同时还提供了负载均衡、故障转移等能力。 Eureka组件的三个角色 服务中心服务提供者服务消费者 Eureka Server:服务器端。提供服务的注册和发现…...
 分页)
原生django raw() 分页
def change_obj_to_dict(self,temp):dict {}dict["wxh_name"] temp.wxh_namedict["types"] temp.typesdict["subject"] temp.subjectdict["ids"] temp.ids# 虽然产品表里没有替代型号,但是通过sql语句的raw()查询可以…...

Android 9.0 Settings 搜索功能屏蔽某个app
1.概述 在9.0的系统rom产品定制化开发过程中,在系统Settings的开发功能中,最近产品需求要求去掉搜索中屏蔽某个app的搜索,就是根据包名,不让搜索出某个app., 在系统setting中,搜索功能中,根据包名过滤掉某个app的搜索功能,所以需要熟悉系统Settings中的搜索的相关功能,…...
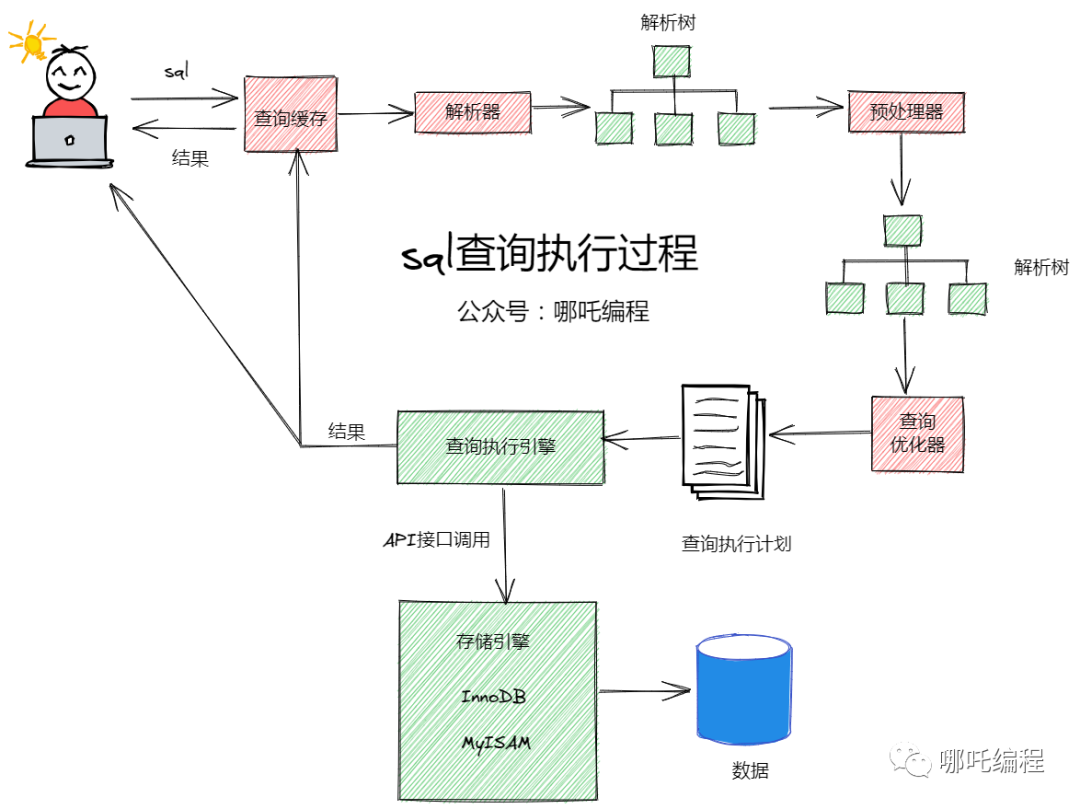
SQL性能优化的47个小技巧,果断收藏!
1、先了解MySQL的执行过程 了解了MySQL的执行过程,我们才知道如何进行sql优化。 客户端发送一条查询语句到服务器; 服务器先查询缓存,如果命中缓存,则立即返回存储在缓存中的数据; 未命中缓存后,MySQL通…...

SE | 哇哦!让人不断感叹真香的数据格式!~
1写在前面 最近在用的包经常涉及到SummarizedExperiment格式的文件,不知道大家有没有遇到过。🤒 一开始觉得这种格式真麻烦,后面搞懂了之后发现真是香啊,爱不释手!~😜 2什么是SummarizedExperiment 这种cla…...

运行Qt后出现无法显示字库问题的解决方案
问题描述:运行后字体出现问题QFontDatabase: Cannot find font directory解决前提: 其实就是移植后字体库中是空的,字没办法进行显示本质就是我们只需要通过某种手段将QT界面中的字母所调用的库进行填充即可此处需要注意的是,必须…...
数据库浅谈之共识算法
数据库浅谈之共识算法 HELLO,各位博友好,我是阿呆 🙈🙈🙈 这里是数据库浅谈系列,收录在专栏 DATABASE 中 😜😜😜 本系列阿呆将记录一些数据库领域相关的知识 …...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...
