2023年CSP-S赛后总结(2023CSP-S题解)
目录
T1
题目描述
输入格式
输出格式
代码
T2
题目描述
输入格式
输出格式
题目描述
输入格式
输出格式
题意翻译
代码
T3
题目背景
题目描述
输入格式
输出格式
代码
T4
题目描述
输入格式
输出格式
总结
T1
题目描述
小 Y 有一把五个拨圈的密码锁。如图所示,每个拨圈上是从 00 到 99 的数字。每个拨圈都是从 00 到 99 的循环,即 99 拨动一个位置后可以变成 00 或 88,
因为校园里比较安全,小 Y 采用的锁车方式是:从正确密码开始,随机转动密码锁仅一次;每次都是以某个幅度仅转动一个拨圈或者同时转动两个相邻的拨圈。
当小 Y 选择同时转动两个相邻拨圈时,两个拨圈转动的幅度相同,即小 Y 可以将密码锁从 0 0 1 1 5 转成 1 1 1 1 5,但不会转成 1 2 1 1 5。
时间久了,小 Y 也担心这么锁车的安全性,所以小 Y 记下了自己锁车后密码锁的 n 个状态,注意这 n 个状态都不是正确密码。
为了检验这么锁车的安全性,小 Y 有多少种可能的正确密码,使得每个正确密码都能够按照他所采用的锁车方式产生锁车后密码锁的全部 �n 个状态。
输入格式
输入的第一行包含一个正整数 n,表示锁车后密码锁的状态数。
接下来 n 行每行包含五个整数,表示一个密码锁的状态。
输出格式
输出一行包含一个整数,表示密码锁的这 n 个状态按照给定的锁车方式能对应多少种正确密码。
这道题第一眼看是数学
当n==1时,一定会输出81
当n>1时,如果任意两组的差异有一组大于二,那么输出0;如果任意两组的差异为二,就要判断他们是否相邻,且差值是否相同,若不成立,则输出0,否则输出10;如果任意两组的差异为一,就要判断是否在同一位置相差,如果是,输出10,否则输出1。
后来,试了试。。。还是暴力,只不过是暴力枚举求交集
下面直接暴搜,上代码
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 10;
int n, ans;
int st[N], ce[N][10];int dis(int x, int y, int xb, int yb) {int ddd = (x - xb + 10) % 10;int dd2 = (y - yb + 10) % 10;//cout << ddd << " " << dd2 << endl;return (ddd == dd2);
}int calc(int id) {int cnt = 0;int id1 = 0, id2 = 0;for(int i = 1; i <= 5;i++) {if(st[i] == ce[id][i]) continue;if(!id1) id1 = i;else if(!id2) id2 = i;cnt++;}if(cnt == 1) return 1;if(cnt > 2) return 0;//cout << id1 << " " << id2 << endl;if(id1 != id2 - 1 && id1 != id2 + 1) return 0;for(int i = 1; i < 5;i++) {if(st[i] != ce[id][i] && st[i + 1] != ce[id][i + 1]) {if(!dis(st[i], st[i + 1], ce[id][i], ce[id][i + 1])) return 0;}}return 1;
}void did() {//for(int i = 1;i <= 5;i++) cout << st[i] << " ";//cout << endl;for(int i = 1;i <= n;i++) {if(!calc(i)) return;}ans++;
}void dfs(int i) {if(i > 5) return did();for(int j = 0;j <= 9;j++) {st[i] = j;dfs(i + 1);st[i] = 0;}}int main() {scanf("%d", &n); for(int i = 1; i <= n;i++) {for(int j = 1;j <= 5;j++) {scanf("%d", &ce[i][j]);}}dfs(1);printf("%d", ans);return 0;
}T2
题目描述
小 L 现在在玩一个低配版本的消消乐,该版本的游戏是一维的,一次也只能消除两 个相邻的元素。
现在,他有一个长度为 n 且仅由小写字母构成的字符串。我们称一个字符串是可消除的,当且仅当可以对这个字符串进行若干次操作,使之成为一个空字符串。
其中每次操作可以从字符串中删除两个相邻的相同字符,操作后剩余字符串会拼接在一起。
小 L 想知道,这个字符串的所有非空连续子串中,有多少个是可消除的。
输入格式
输入的第一行包含一个正整数 n,表示字符串的长度。
输入的第二行包含一个长度为 n 且仅由小写字母构成的的字符串,表示题目中询问的字符串。
输出格式
输出一行包含一个整数,表示题目询问的答案。
这道题和CF重了,所以也贴一下CF的题面
题目描述
Let's look at the following process: initially you have an empty stack and an array s of the length l . You are trying to push array elements to the stack in the order s1,s2,s3,…sl . Moreover, if the stack is empty or the element at the top of this stack is not equal to the current element, then you just push the current element to the top of the stack. Otherwise, you don't push the current element to the stack and, moreover, pop the top element of the stack.
If after this process the stack remains empty, the array s is considered stack exterminable.
There are samples of stack exterminable arrays:
- [1,1][1,1] ;
- [2,1,1,2][2,1,1,2] ;
- [1,1,2,2][1,1,2,2] ;
- [1,3,3,1,2,2][1,3,3,1,2,2] ;
- [3,1,3,3,1,3][3,1,3,3,1,3] ;
- [3,3,3,3,3,3][3,3,3,3,3,3] ;
- [5,1,2,2,1,4,4,5][5,1,2,2,1,4,4,5] ;
Let's consider the changing of stack more details if s=[5,1,2,2,1,4,4,5] (the top of stack is highlighted).
- after pushing s1=5 the stack turn into [5][5] ;
- after pushing s2=1 the stack turn into [5,1][5,1] ;
- after pushing s3=2 the stack turn into [5,1,2][5,1,2] ;
- after pushing s4=2 the stack turn into [5,1][5,1] ;
- after pushing s5=1 the stack turn into [5][5] ;
- after pushing s6=4 the stack turn into [5,4][5,4] ;
- after pushing s7=4 the stack turn into [5][5] ;
- after pushing s8=5 the stack is empty.
You are given an array a1,a2,…,an . You have to calculate the number of its subarrays which are stack exterminable.
Note, that you have to answer q independent queries.
输入格式
The first line contains one integer q ( 1≤q≤3⋅105 ) — the number of queries.
The first line of each query contains one integer n ( 1≤n≤3⋅105 ) — the length of array a .
The second line of each query contains n integers a1,a2,…,an ( 1≤ai≤n ) — the elements.
It is guaranteed that the sum of all n over all queries does not exceed 3⋅1053⋅105 .
输出格式
For each test case print one integer in single line — the number of stack exterminable subarrays of the array a .
题意翻译
给一个序列进行栈操作,从左到右入栈,若当前入栈元素等于栈顶元素则栈顶元素出栈,否则当前元素入栈。若进行完操作后栈为空,这说这个序列是可以被消除的。
给你一个长度为n的序列a,问a有多少子串是可以被消除的。
这道题用括号匹配O(2^{_{n}})做,能得50分
但是,我们要冲正解
我们考虑保存一个mi,j 表示一个最大的 mi,j 满足 mi,j=j 且mi,j+1,i 可以消除,然后就可以快速求 pi 了。
那么怎么维护 m 呢?我们如果找到了合法的 pi,可以考虑直接令 mi=mpi−1,看似时间复杂度爆炸,其实后面用不到mpi−1,可以直接交换,时间复杂度为 O(1),然后再把不同的项改改就行了。
下面上代码
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
string s;
int n, ans, a[2000005], p[2000005], f[2000005];
map<int, int> m[2000005];
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);scanf("%lld", &n);cin >> s;for (int i = 0; i < n; i++) {a[i + 1] = s[i] - 'a';m[i + 1].clear();f[i + 1] = 0;p[i + 1] = -1;}for (int i = 1; i <= n; i++) {if (m[i - 1].count(a[i])) {int t = m[i - 1][a[i]];p[i] = t;swap(m[i], m[t - 1]);if (t != 1) {m[i][a[t - 1]] = t - 1;}}m[i][a[i]] = i;}for (int i = 1; i <= n; i++) {if (p[i] == -1) {continue;}f[i] = f[p[i] - 1] + 1;ans += f[i];}printf("%lld\n", ans);return 0;
}T3
题目背景
在 C++ 等高级语言中,除了 int 和 float 等基本类型外,通常还可以自定义结构体类型。在本题当中,你需要模拟一种类似 C++ 的高级语言的结构体定义方式,并计算出相应的内存占用等信息。
题目描述
在这种语言中,基本类型共有 44 种:
byte, short, int, long,分别占据 1,2,4,81,2,4,8 字节的空间。定义一个结构体类型时,需要给出类型名和成员,其中每个成员需要按顺序给出类型和名称。类型可以为基本类型,也可以为先前定义过的结构体类型。注意,定义结构体类型时不会定义具体元素,即不占用内存。
定义一个元素时,需要给出元素的类型和名称。元素将按照以下规则占据内存:
- 元素内的所有成员将按照定义时给出的顺序在内存中排布,对于类型为结构体的成员同理。
- 为了保证内存访问的效率,元素的地址占用需要满足对齐规则,即任何类型的大小和该类型元素在内存中的起始地址均应对齐到该类型对齐要求的整数倍。具体而言:
- 对于基本类型:对齐要求等于其占据空间大小,如
int类型需要对齐到 44 字节,其余同理。- 对于结构体类型:对齐要求等于其成员的对齐要求的最大值,如一个含有
int和short的结构体类型需要对齐到 44 字节。以下是一个例子(以 C++ 语言的格式书写):
struct d {short a;int b;short c; }; d e;该代码定义了结构体类型
d与元素e。元素e包含三个成员e.a, e.b, e.c,分别占据第 0∼10∼1,4∼74∼7,8∼98∼9 字节的地址。由于类型d需要对齐到 44 字节,因此e占据了第 0∼110∼11 字节的地址,大小为 1212 字节。你需要处理 n 次操作,每次操作为以下四种之一:
定义一个结构体类型。具体而言,给定正整数 k 与字符串 ,1,1,…,,s,t1,n1,…,tk,nk,其中 k 表示该类型的成员数量,s 表示该类型的类型名,1,2,…,t1,t2,…,tk 按顺序分别表示每个成员的类型,1,2,…,n1,n2,…,nk 按顺序分别表示每个成员的名称。你需要输出该结构体类型的大小和对齐要求,用一个空格分隔。
定义一个元素,具体而言,给定字符串 ,t,n 分别表示该元素的类型与名称。所有被定义的元素将按顺序,从内存地址为 00 开始依次排开,并需要满足地址对齐规则。你需要输出新定义的元素的起始地址。
访问某个元素。具体而言,给定字符串 s,表示所访问的元素。与 C++ 等语言相同,采用
.来访问结构体类型的成员。如a.b.c,表示a是一个已定义的元素,它是一个结构体类型,有一个名称为b的成员,它也是一个结构体类型,有一个名称为c的成员。你需要输出如上被访问的最内层元素的起始地址。访问某个内存地址。具体而言,给定非负整数addr,表示所访问的地址,你需要判断是否存在一个基本类型的元素占据了该地址。若是,则按操作 3 中的访问元素格式输出该元素;否则输出
ERR。输入格式
第 11 行:一个正整数 n,表示操作的数量。
接下来若干行,依次描述每个操作,每行第一个正整数 op 表示操作类型:
若 op=1,首先输入一个字符串 s 与一个正整数 k,表示类型名与成员数量,接下来 k 行每行输入两个字符串 ,ti,ni,依次表示每个成员的类型与名称。
若 op=2,输入两个字符串 ,t,n,表示该元素的类型与名称。
若 op=3,输入一个字符串 s,表示所访问的元素。
若 op=4,输入一个非负整数 addr,表示所访问的地址。
输出格式
输出 n 行,依次表示每个操作的输出结果,输出要求如题目描述中所述。
这道题在考场上想做,又不敢做,纠结了很久。下来一想,才发现是纯纯的大模拟。
废话不多说,直接上代码(模拟题别抄)
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
struct Node {int k, s[105], a[105], o[105], maxn, siz;string tp[105], nm[105];string id;
} f[105];
struct node {int s, a, b;string tp, nm;
} g[105];
map<string, int> mp1, mp2, mp;
signed main() {ios::sync_with_stdio(false);mp1["byte"] = 1, mp1["short"] = 2, mp1["int"] = 4, mp1["long"] = 8, mp2["byte"] = 1, mp2["short"] = 2, mp2["int"] = 4, mp2["long"] = 8;int cnt = 0, tot = 0, q;cin >> q;while (q--) {int op;cin >> op;if (op == 1) {cnt++;cin >> f[cnt].id;cin >> f[cnt].k;for (int i = 1; i <= f[cnt].k; i++) {cin >> f[cnt].tp[i] >> f[cnt].nm[i];int lst = f[cnt].o[i - 1] + f[cnt].s[i - 1];f[cnt].a[i] = mp2[f[cnt].tp[i]];f[cnt].s[i] = mp1[f[cnt].tp[i]];if (lst % f[cnt].a[i]) {lst += (f[cnt].a[i] - lst % f[cnt].a[i]);}f[cnt].o[i] = lst;f[cnt].maxn = max(f[cnt].maxn, f[cnt].a[i]);}int lst = f[cnt].o[f[cnt].k] + f[cnt].s[f[cnt].k];if (lst % f[cnt].maxn) {lst += (f[cnt].maxn - lst % f[cnt].maxn);}f[cnt].siz = lst;mp1[f[cnt].id] = f[cnt].siz;mp2[f[cnt].id] = f[cnt].maxn;mp[f[cnt].id] = cnt;cout << f[cnt].siz << " " << f[cnt].maxn << "\n";} else if (op == 2) {tot++;cin >> g[tot].tp >> g[tot].nm;g[tot].a = mp2[g[tot].tp];g[tot].s = mp1[g[tot].tp];int lst = g[tot - 1].b + g[tot - 1].s;if (lst % g[tot].a) lst += (g[tot].a - lst % g[tot].a);g[tot].b = lst;cout << g[tot].b << "\n";} else if (op == 3) {string s;cin >> s;s += ".";string cat = "";int len = s.size(), tp;for (int i = 0; i < len; i++) {if (s[i] == '.') {tp = i + 1;break;}cat += s[i];}int sum = 0, abab;for (int i = 1; i <= tot; i++) {if (g[i].nm == cat) {sum = g[i].b;abab = mp[g[i].tp];break;}}if (abab == 0) {cout << sum << "\n";continue;}cat = "";for (int i = tp; i < len; i++) {if (s[i] == '.') {for (int j = 1; j <= f[abab].k; j++) {if (f[abab].nm[j] == cat) {sum += f[abab].o[j];abab = mp[f[abab].tp[j]];break;}}if (abab == 0) {break;}cat = "";continue;}cat += s[i];}cout << sum << "\n";} else {int cat;cin >> cat;string sum = "", ty;int abab = -1;for (int i = 1; i <= tot; i++) {if (g[i].b + g[i].s > cat && g[i].b <= cat) {abab = mp[g[i].tp];cat -= g[i].b;sum += g[i].nm;ty = g[i].tp;break;}}if (abab == -1) {cout << "ERR\n";continue;}if (!abab) {if (mp1[ty] > cat) {cout << sum << "\n";} else {cout << "ERR\n";}continue;}sum += ".";while (1) {if (cat < 0) {cout << "ERR\n";break;}int ff = 0;for (int i = 1; i <= f[abab].k; i++) {if (f[abab].o[i] + f[abab].s[i] > cat && f[abab].o[i] <= cat) {cat -= f[abab].o[i];sum += f[abab].nm[i];ty = f[abab].tp[i];abab = mp[f[abab].tp[i]];ff = 1;break;}}if (!ff) {cout << "ERR\n";break;}if (!abab) {if (mp1[ty] > cat) {cout << sum << "\n";} else {cout << "ERR\n";}break;}sum += ".";}}}return 0;
}T4
题目描述
你是一个森林养护员,有一天,你接到了一个任务:在一片森林内的地块上种树,并养护至树木长到指定的高度。
森林的地图有 n 片地块,其中 1 号地块连接森林的入口。共有 n−1 条道路连接这些地块,使得每片地块都能通过道路互相到达。最开始,每片地块上都没有树木。
你的目标是:在每片地块上均种植一棵树木,并使得 i 号地块上的树的高度生长到不低于 ai 米。
你每天可以选择一个未种树且与某个已种树的地块直接邻接(即通过单条道路相连)的地块,种一棵高度为 0 米的树。如果所有地块均已种过树,则你当天不进行任何操作。特别地,第 1 天你只能在 1 号空地种树。
对每个地块而言,从该地块被种下树的当天开始,该地块上的树每天都会生长一定的高度。由于气候和土壤条件不同,在第 x 天,i 号地块上的树会长高 max(bi+x×ci,1) 米。注意这里的 x 是从整个任务的第一天,而非种下这棵树的第一天开始计算。
你想知道:最少需要多少天能够完成你的任务?
输入格式
输入的第一行包含一个正整数 n,表示森林的地块数量。
接下来 n 行:每行包含三个整数 ai,bi,ci,分别描述一片地块,含义如题目描述中所述。
接下来 n−1 行:每行包含两个正整数 ui,vi,表示一条连接地块 ui 和 vi 的道路。
输出格式
输出一行仅包含一个正整数,表示完成任务所需的最少天数。
这道题我在考场上第一眼想用生长天数进行排序,后来才发现x的值会变,最后用的贪心骗分。
代码
后续更新(等我AC了再说)
总结
这套卷子码量太大,重点在T2、T4
相关文章:

2023年CSP-S赛后总结(2023CSP-S题解)
目录 T1 题目描述 输入格式 输出格式 代码 T2 题目描述 输入格式 输出格式 题目描述 输入格式 输出格式 题意翻译 代码 T3 题目背景 题目描述 输入格式 输出格式 代码 T4 题目描述 输入格式 输出格式 总结 T1 题目描述 小 Y 有一把五个拨圈的密码锁。…...
Django viewsets 视图集与 router 路由实现评论接口开发
正常来说遵循restful风格编写接口,定义一个类包含了 get post delete put 四种请求方式,这四种请求方式是不能重复的 例如:获取单条记录和多条记录使用的方式都是get,如果两个都要实现的话那么得定义两个类,因为在同一个类中不能有…...
RCE 远程代码执行漏洞分析
RCE 漏洞 1.漏洞描述 Remote Command/Code Execute 远程命令执行/远程代码执行漏洞 这种漏洞通常出现在应用程序或操作系统中,攻击者可以通过利用漏洞注入恶意代码,并在受攻击的系统上执行任意命令。 2.漏洞场景 PHP 代码执行PHP 代码注入OS 命令执…...
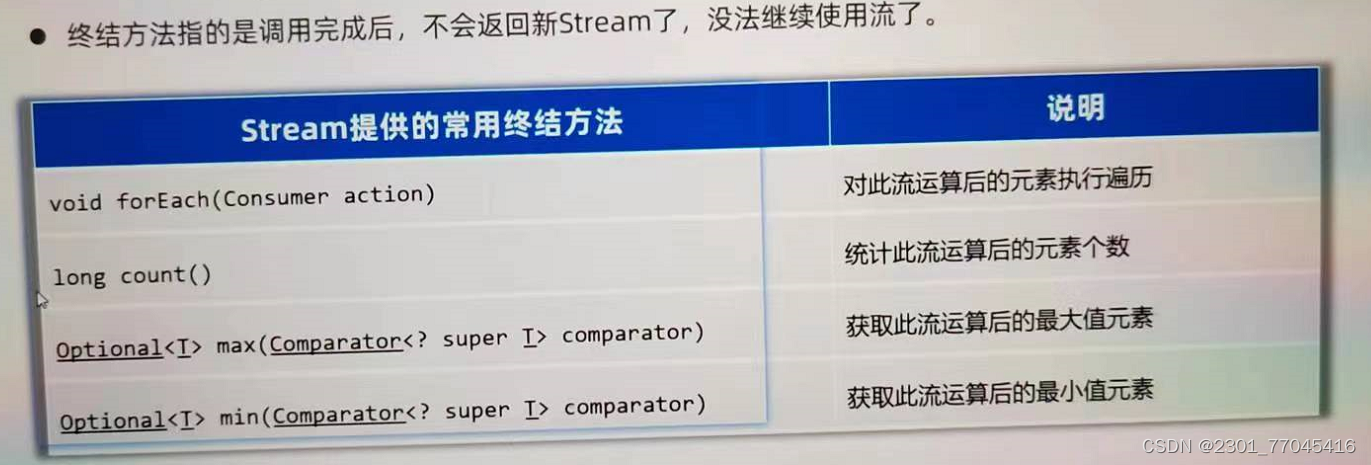
JDK8新特性:Stream流
目录 1.获取Stream流 2.Stream流常见的中间方法 3.Stream流常见的终结方法 1、 Stream 是什么?有什么作用?结合了什么技术? ●也叫 Stream 流,是Jdk8开始新增的一套 API ( java . util . stream .*),可以用于操作集…...

【.net core】yisha框架单页面双列表联动效果示例
gridTable1列表数据为gridTable别表数据的子数据,点击gridTable时gridTable1列表数据更新, {Layout "~/Views/Shared/_Index.cshtml";} <div class"container-div"><div class"row"><div id"search…...

01. 板载硬件资源和开发环境
一、板载硬件资源 STM32F4VGT6-DISCOVERY硬件资源如下: (1). STM32F407VGT6微控制器有1M的FLASH存储器,192K的RAM,LQFP100封装 (2). 板上的ST-LINK_V2可以使用选择的方式把套件切换成一个独立的ST-LINK/V2来 使用(可以使用SWD…...
)
BlobDetector的使用与参数说明(OpenCV/C++)
通过opencv的BlobDetector方法可以检测斑点、圆点、椭圆等形状 以下是使用方式及代码说明: 1、导入必要的OpenCV库和头文件。 #include <opencv2/opencv.hpp> #include <opencv2/blob/blobdetector.hpp>2、读取图像并将其转换为灰度图像。 cv::Mat…...

行为型模式-空对象模式
在空对象模式(Null Object Pattern)中,一个空对象取代 NULL 对象实例的检查。Null 对象不是检查空值,而是反应一个不做任何动作的关系。这样的 Null 对象也可以在数据不可用的时候提供默认的行为。 在空对象模式中,我…...

爬虫采集如何解决ip被限制的问题呢?
在进行爬虫采集的过程中,很多开发者会遇到IP被限制的问题,这给采集工作带来了很大的不便。那么,如何解决这个问题呢?下面我们将从以下几个方面进行探讨。 一、了解网站的反爬机制 首先,我们需要了解目标网站的反爬机制…...

【ARM AMBA Q_Channel 详细介绍】
文章目录 1.1 Q_Channel 概述1.2 Q-Channel1.2.1 Q-Channel 接口1.2.2 Q-Channel 接口的握手状态1.2.3 握手信号规则 1.3 P_Channel的握手协议1.3.1 device 接受 PMU 的 power 请求1.3.2 device 拒绝 PMU 的 power 请求 1.4 device 复位信号与 Q _Channel 的结合1.4.1 RESETn 复…...
PDF Reader Pro v2.9.8(pdf编辑阅读器)
PDF Reader Pro是一款PDF阅读和编辑软件,具有以下特点: 界面设计简洁,易于上手。软件界面直观清晰,用户可以轻松浏览文档,编辑注释和填写表单。功能强大,提供了多种PDF处理工具,包括阅读、注释…...

【机器学习可解释性】1.模型洞察的价值
机器学习可解释性 1.模型洞察的价值2.排列的重要性3.部分图表4.SHAP Value5.SHAP Value 高级使用 正文 前言 本文是 kaggle上机器学习可解释性课程,共五部分,除第一部分介绍外,每部分包括辅导和练习。 此为第一部分,原文链接 如…...

网络安全保险行业面临的挑战与变革
保险业内大多数资产类别的数据可以追溯到几个世纪以前;然而,网络安全保险业仍处于初级阶段。由于勒索软件攻击、高度复杂的黑客和昂贵的数据泄漏事件不断增加,许多网络安全保险提供商开始感到害怕继续承保更多业务。 保险行业 根据最近的路…...

如何提高系统的可用性/高可用
提高系统可用性常用的一些方法,有缓存、异步、重试、幂等、补偿、熔断、降级、限流。 缓存 缓存的速度,比数据库快很多,添加缓存是简单有效的做法。 注意缓存与数据库的一致性,数据表记录变更时记得处理缓存。 Redis缓存的示例&…...
)
PCA和LDA数据降维计算(含数学例子推导过程)
PCA算法和LDA算法可以用于对数据进行降维,例如可以把一个2维的数据降低维度到一维,本文通过举例子来对PCA算法和LDA算法的计算过程进行教学展示。 PCA算法计算过程(文字版,想看具体计算下面有例子) 1.将原始数据排列成n行m列的矩阵…...
题目 1053: 二级C语言-平均值计算(python详解)——练气三层初期
✨博主:命运之光 🦄专栏:算法修炼之练气篇(C\C版) 🍓专栏:算法修炼之筑基篇(C\C版) 🍒专栏:算法修炼之练气篇(Python版) ✨…...
Python —— UI自动化之Page Object模式
1、Page Object模式简介 1、二层模型 Page Object Model(页面对象模型), 或者也可称之为POM。在UI自动化测试广泛使用的一种分层设计 模式。核心是通过页面层封装所有的页面元素及操作,测试用例层通过调用页面层操作组装业务逻辑。 1、实战 …...

职能篇—自动驾驶产品经理
自动驾驶产品开发流程 在讲自动驾驶产品经理之前,先简单了解一下自动驾驶的开发体系。如上图所示,从产品需求开始,经由系统需求、系统架构、软件需求、软件架构,最终分解到软件代码实现模块,再经由MIL、SIL、HIL、VIL完…...

ubuntu安装golang
看版本:https://go.dev/dl/ 下载: wget https://go.dev/dl/go1.21.3.linux-amd64.tar.gz卸载已有的go,可以apt remove go,也可以which go之后删除那个go文件,然后: rm -rf /usr/local/go && tar…...

ES 8 新特性
1. async 和 await async 和 await 两种语法结合可以让异步代码像同步代码一样。(即:看起来是同步的,实质上是异步的。) 先从字面意思理解,async 意为异步,可以用于声明一个函数前,该函数是异步的。await 意为等待,即等待一个异步方法完成。 1.1 async async 声明(…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...
