【数据结构】手撕红黑树


目录
一、红黑树简介
1、红黑树的简介
2、红黑树的性质
二、红黑树的插入(看叔叔的颜色就行)
1、为什么新插入的节点必须给红色?
2、插入红色节点后,判定红黑树性质是否被破坏
2.1情况一:uncle存在且为红
2.2情况二:uncle不存在/存在且为黑(直线)
2.3情况三:uncle不存在/存在且为黑(折线)
2.4总结
3、红黑树插入代码
三、红黑树整体代码
一、红黑树简介
1、红黑树的简介
红黑树和AVL树一样,因其逻辑复杂,面试时现场要求手撕就是纯纯刁难面试者。但某大厂面试官曾要求某些求职者现场手撕红黑树(我赌5毛,让面试官撕,他也撕不出来,而且你家员工上班手搓红黑树啊?),随后求职遭遇被发到网上吐槽,这便有了“手撕红黑树”的梗,也让红黑树成为了知名度最高的数据结构。(话虽如此,对于红黑树的性质、插入思想等概念还是需要掌握的)
2、红黑树的性质
红黑树本质也是一种二叉搜索树。底层结构需要使用二叉搜索树的地方,基本上都会使用红黑树来实现,而AVL树也因此坐上了冷板凳。
红黑树通过在每个节点上添加一个存储位,用于存储“RED”或“BLACK”。通过节点上红/黑颜色限制,确保最长路径不超过最短路径的两倍,因而它是接近平衡的树形结构。最短路径:全黑;最长路径:一黑一红交替。
1、红黑树的根节点是黑色的;
2、没有连续的红色节点(如果某个节点为红色,则它的左右孩子必须是黑色)
3、无论哪个节点,其每条路径的黑色节点数量相同;
4、所有的空节点(NIL节点)可以认为是黑色的。
最优情况:全黑或每条路径都是一黑一红的满二叉树,高度logN
最差情况:每颗子树左子树全黑,右子树一黑一红。高度2*logN。
可以发现,最坏情况的时间复杂度和AVL树一样,都是O(logN),但是红黑树这种近似平衡的结构减少了大量旋转,综合性能优于AVL树。
二、红黑树的插入(看叔叔的颜色就行)
1、为什么新插入的节点必须给红色?
新节点给红色,可能会违反上面说的红黑树性质2;如果新节点给黑色,必定会违反性质3。
2、插入红色节点后,判定红黑树性质是否被破坏
情况一调整后可能变成情况一、情况二、情况三。
2.1情况一:uncle存在且为红
这种情况cur、parent、grandfather都是确定颜色的,唯独uncle的颜色是不确定的。
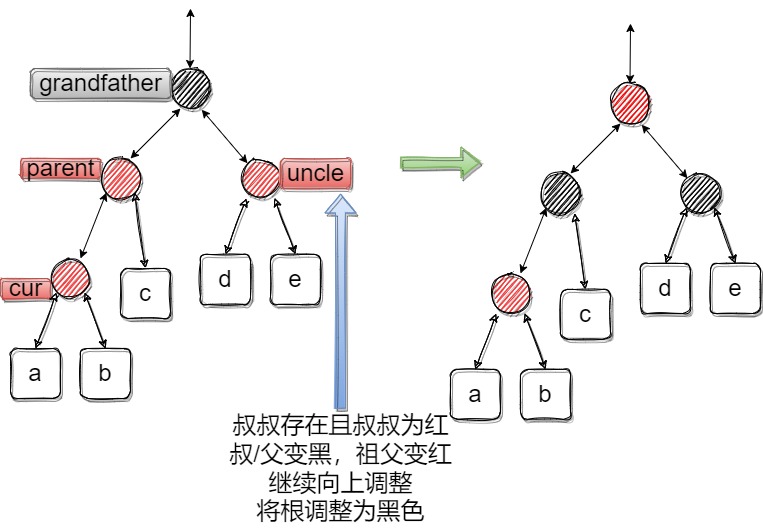
可以这么想:cur为红那么就需要将parent变为黑;parent变黑需要控制每条路径上黑节点的数量相同,那么就要把uncle变黑;如果grandfather不是根,需要反转为红,用以控制路径黑节点数量相同。继续向上调整即可。
2.2情况二:uncle不存在/存在且为黑(直线)
uncle的情况分两种。
uncle不存在,则cur为插入节点,单旋即可。
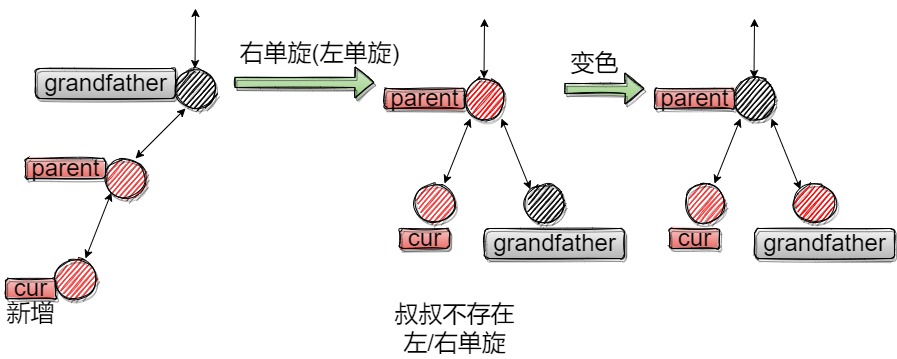
uncle存在且为黑是第一种情况变过来的。

2.3情况三:uncle不存在/存在且为黑(折线)
uncle的情况分两种。
uncle不存在,则cur为插入节点,两次单旋即可。
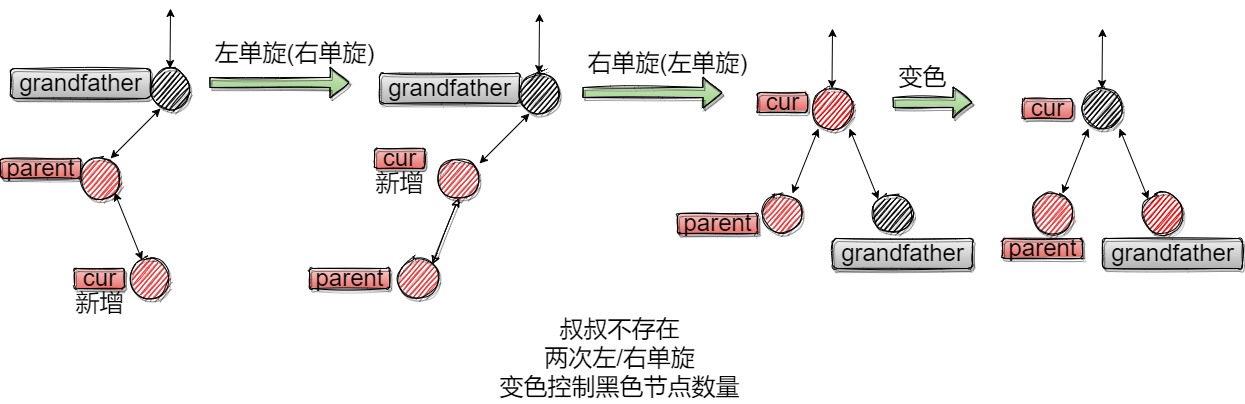
uncle存在且为黑,先掰直

2.4总结
插入新节点时,父节点为红,看叔叔的颜色。
1、叔叔存在且为红,变色,向上调整(可能变为三种情况中的任意一种)
2、叔叔不存在/存在且为黑,直线。单旋+变色
3、叔叔不存在/存在且为黑,折线,两次单旋+变色
3、红黑树插入代码
bool Insert(const pair<K,V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根节点给黑色return true;}//_root不为空Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else//相等说明元素相同,插入失败return false;}//开始插入cur = new Node(kv);cur->_col = RED;//新插入节点给红色,可能违反规则。如果给黑色会导致其他路径的黑色节点数量不相同,必定违反规则。 if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;//维护cur的父指针}else{parent->_left = cur;cur->_parent = parent;}//调整while (parent&&parent->_col == RED){Node* grandfather = parent->_parent;//找到祖父if (grandfather->_left == parent)//如果父亲是祖父的左孩子{Node* uncle = grandfather->_right;//找到叔叔//情况一:叔叔存在且为红if (uncle != nullptr && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//情况二或情况三{if (cur == parent->_left)//情况二,直线{RotateRight(grandfather);//右单旋parent->_col = BLACK;grandfather->_col = RED;}else//情况三,折线{RotateLeft(parent);//左单旋RotateRight(grandfather);//右单旋cur->_col = BLACK;grandfather->_col = RED;}break;}}else//如果父亲是祖父的右孩子{Node* uncle = grandfather->_left;if (uncle != nullptr && uncle->_col == RED){parent->_col =uncle->_col= BLACK;grandfather->_col = RED; cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right)//情况二,直线{//g// p// cRotateLeft(grandfather);//左单旋parent->_col = BLACK;grandfather->_col = RED;}else//情况三,折线{//g// p//c RotateRight(parent);//右单旋RotateLeft(grandfather);//左单旋cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col=BLACK;return true;
}三、红黑树整体代码
#pragma once
#include <iostream>
#include <map>
#include <set>
#include <string>
using namespace std;
enum Color
{RED,BLACK,
};
template <class K,class V>
struct RBTreeNode
{RBTreeNode(const pair<K,V>& kv):_parent(nullptr),_left(nullptr),_right(nullptr),_kv(kv),_col(RED){}RBTreeNode<K,V>* _parent;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;pair<K, V> _kv;Color _col;
};
template <class K, class V>
class RBTree
{
public:typedef RBTreeNode<K,V> Node;bool Insert(const pair<K,V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根节点给黑色return true;}//_root不为空Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else//相等说明元素相同,插入失败return false;}//开始插入cur = new Node(kv);cur->_col = RED;//新插入节点给红色,可能违反规则。如果给黑色会导致其他路径的黑色节点数量不相同,必定违反规则。 if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;//维护cur的父指针}else{parent->_left = cur;cur->_parent = parent;}//调整while (parent&&parent->_col == RED){Node* grandfather = parent->_parent;//找到祖父if (grandfather->_left == parent)//如果父亲是祖父的左孩子{Node* uncle = grandfather->_right;//找到叔叔//情况一:叔叔存在且为红if (uncle != nullptr && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//情况二或情况三{if (cur == parent->_left)//情况二,直线{RotateRight(grandfather);//右单旋parent->_col = BLACK;grandfather->_col = RED;}else//情况三,折线{RotateLeft(parent);//左单旋RotateRight(grandfather);//右单旋cur->_col = BLACK;grandfather->_col = RED;}break;}}else//如果父亲是祖父的右孩子{Node* uncle = grandfather->_left;if (uncle != nullptr && uncle->_col == RED){parent->_col =uncle->_col= BLACK;grandfather->_col = RED; cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right)//情况二,直线{//g// p// cRotateLeft(grandfather);//左单旋parent->_col = BLACK;grandfather->_col = RED;}else//情况三,折线{//g// p//c RotateRight(parent);//右单旋RotateLeft(grandfather);//左单旋cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col=BLACK;return true;}void Inorder(){_Inorder(_root);}bool IsBalance(){return _IsBalance();}
private:void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}bool Check(Node* root){if (root == nullptr)return true;if (root->_col == RED && root->_parent->_col == RED){cout << "父子均为红" << endl;return false;}return Check(root->_left) && Check(root->_right);}bool _IsBalance(){if (_root == nullptr)return true;if (_root->_col != BLACK){return false;}return Check(_root);}void RotateLeft(Node* parent)//左单旋{Node* grandfather = parent->_parent;Node* cur = parent->_right;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (grandfather->_left == parent)//需要判定parent原来属于grandfather的哪一边grandfather->_left = cur;elsegrandfather->_right = cur;cur->_parent = grandfather;}parent->_right = cur->_left;if (cur->_left != nullptr)cur->_left->_parent = parent;cur->_left = parent;parent->_parent = cur;}void RotateRight(Node* parent)//右单旋{Node* grandfather = parent->_parent;Node* cur = parent->_left;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (grandfather->_left == parent){grandfather->_left = cur;cur->_parent = grandfather;}else{grandfather->_right = cur;cur->_parent = grandfather;}}parent->_parent = cur;parent->_left = cur->_right;if (cur->_right != nullptr)cur->_right->_parent = parent;cur->_right = parent;}
private:Node* _root=nullptr;
};
void TestAVLTree()
{//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };//int a[] = { 9,8,7,6,5,4,3,2,1};RBTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.Inorder();//cout << t.IsBalance() << endl;
}相关文章:

【数据结构】手撕红黑树
目录 一、红黑树简介 1、红黑树的简介 2、红黑树的性质 二、红黑树的插入(看叔叔的颜色就行) 1、为什么新插入的节点必须给红色? 2、插入红色节点后,判定红黑树性质是否被破坏 2.1情况一:uncle存在且为红 2.2情…...

Linux基础命令-which查找命令文件位置
文章目录 which 命令功能 语法格式 基本参数 参考实例 1)查找chmod命令的文件位置 2)查找chmod命令的所有路径 3)一次性查找多个命令路径 4)组合其他命令一起使用 5)显示命令的版本信息 命令总结 which 命…...

在Python中,导入拓展库的规范如下:
在Python中,导入拓展库的规范如下: Import 模块名 [as 别名] from 模块名Import 对象名 [as 别名] from 模块名 import * 1.导入标准库和第三方库的方式应该不同 Python标准库已经默认安装在Python解释器中,因此在导入标准库时不需要…...
SEATA是什么?它的四种分布式事务模式
一、SEATA是什么? Seata 是一款开源的分布式事务解决方案,致力于提供高性能和简单易用的分布式事务服务。Seata 将为用户提供了 AT、TCC、SAGA 和 XA 事务模式,为用户打造一站式的分布式解决方案。 在继续学习使用SEATA之前,对s…...

【华为OD机试模拟题】用 C++ 实现 - 去重求和(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 获得完美走位(2023.Q1) 文章目录 最近更新的博客使用说明去重求和题目输入输出示例一输入输出说明示例一输入输出说明Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。…...

如何用 chatGPT,给大家来一个自我介绍
大家好,我是不吃西红柿的无线机械键盘,我的名字叫 Keychron K3 Pro。今天,我通过西红柿主人的手,使用 chatGPT 来介绍一下我自己。我的与众不同 我是由精密机械元件制作而成,并采用抗键渗设计,以提供更快、…...
进程管理之基本概念
目录 关于进程的基本概念 进程描述符 查看进程 进程标识 进程的生命周期 僵尸进程、孤儿进程 写时拷贝技术 fork()函数 vfork()函数 终止进程 进程优先级和权重 进程地址空间 关于进程的基本概念 进程和程序是操作系统领域的两个重要的概念,进程是执行…...
nginx安装部署实战手册
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录一、虚拟机安装nginx1.下载安装包2.安装编译工具和库文件3.编译安装4.启动nginx5.访问首页6.开机自启结尾一、虚拟机安装nginx 1.下载安装包 官网下载地址…...

XXL-JOB任务调度平台
什么是xxl-job? xxl-job是一个分布式的任务调度平台,其核心设计目标是:学习简单、开发迅速、轻量级、易扩展,现在已经开放源代码并接入多家公司的线上产品线,开箱即用。xxl是xxl-job的开发者大众点评的许雪里名称的拼…...

android UI优化的基本原理和实战方法
任何Android应用都需要UI跟用户交互.UI是否好坏更是直接影响到用户的体验.如今UI的优化视乎是应用开发中一个绕不过去的话题。所以本篇文章小编带大家全面了解Android ui优化的主要知识和优化方法。 一、UI优化 UI优化知识点主要分为三部分: 第一部分,…...

指针的进阶【中篇】
文章目录📀4.数组参数💿4.1.一维数组传参💿4.2.二维数组传参📀5.指针参数💿5.1.一级指针传参💿5.2.二级指针传参📀6.函数指针💿6.1. 代码1💿6.2. 代码2📀7.函…...

华为OD机试题,用 Java 解【删除字符串中出现次数最少的字符】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

【C语言每日一题】猜名次
【C语言每日一题】—— 猜名次😎😎😎 💡前言🌞: 💛猜名次题目💛 💪 解题思路的分享💪 😊题目源码的分享😊 👉 本菜鸡…...

89. 格雷编码
89. 格雷编码题目数学公式动态规划回溯题目 传送门:https://leetcode.cn/problems/gray-code/ 数学公式 int gray(int n) { // 计算第n位格雷码公式return n ^ (n >> 1); }然后你写一个for循环,计算从1到n的所有格雷码,添加到答…...

线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解
相关文章 K近邻算法和KD树详细介绍及其原理详解朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解决策树算法和CART决策树算法详细介绍及其原理详解线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解 文章目录相关文章前言一、线性回归二、逻辑斯谛回归总结前言 今天给大家…...

【网络原理8】HTTP请求篇
在上一篇文章当中,我们也提到了什么是HTTP。 每一个HTTP请求,都会对应一个HTTP响应。 下面这一篇文章,将聊一下HTTP请求的一些内容 目录 一、URL 第一部分:协议名称 第二部分:认证信息(新的版本已经没有了) 第三部分…...
Playbook的用法
目录 Playbook Playbook 与 Ad-Hoc 对比 YAML 语言特性 YAML语法简介 支持的数据类型 写法格式 1 scalar 标量 建议缩进两个空格,可多 2 Dictionary 字典 3 List 列表 三种常见的数据格式 Playbook 核心组件 不要用 tab 可以#注释 hosts remote_us…...
APP优化 —— MMAP内存映射
mmap 一种内存映射文件的方法 mmap将一个文件或者其它对象映射进内存。文件被映射到多个页上,如果文件的大小不是所有页的大小之和,最后一个页不被使用的空间将会清零。mmap在用户空间映射调用系统中作用很大。 头文件 <sys/mman.h> 函数原型 v…...

paddle.vision 与 torchvision 中的box NMS使用方式
torchvision 中有多个用于计算 BBox NMS 的 API, 在本篇氵文中, 使用 torchvision.ops.boxes.batched_nmspaddle.vision 中通过 paddle.vision.ops.nms 来进行多个 Box 的 NMS 操作 1. torchvision 中 batched_nms 操作 torchvision batched_nms def batched_nms(boxes: to…...
php mysql校园帮忙领取快递平台
1、后台管理员用户名hsg 密码hsg 2、开发语言:PHP,数据库为MySql 3、数据库连接字符串在conn.php中修改 4、运行环境wamp5.1.7或者appserv2.5.9 5.程序编码gbk.不支持php5.3以上版本 6.本人发布的程序一律享有免费运行一次…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...
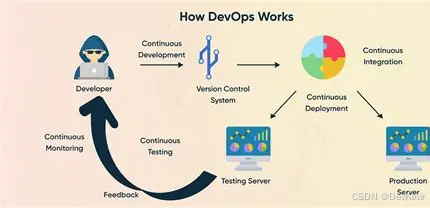
持续交付的进化:从DevOps到AI驱动的IT新动能
文章目录 一、持续交付的本质:从手动到自动的交付飞跃关键特性案例:电商平台的高效部署 二、持续交付的演进:从CI到AI驱动的未来发展历程 中国…...

前端异步编程全场景解读
前端异步编程是现代Web开发的核心,它解决了浏览器单线程执行带来的UI阻塞问题。以下从多个维度进行深度解析: 一、异步编程的核心概念 JavaScript的执行环境是单线程的,这意味着在同一时间只能执行一个任务。为了不阻塞主线程,J…...
