2023NOIP A层联测17 黑暗料理
题目大意
给出一个长度为 n n n的序列 a i a_i ai,要求删去若干个数,使得剩下的数中任意两个数都不是质数。在满足条件的情况下最多能保留几个数。
有 T T T组数据。
1 ≤ T ≤ 4 , 1 ≤ n ≤ 750 , 1 ≤ a i ≤ 1 0 9 1\leq T\leq 4,1\leq n\leq 750,1\leq a_i\leq 10^9 1≤T≤4,1≤n≤750,1≤ai≤109
时间限制 2000 m s 2000ms 2000ms,空间限制 512 M B 512MB 512MB
题解
首先,如果一个数 k k k不是质数,那一定 k k k存在一个质因数 p p p满足 p ≤ k p\leq \sqrt k p≤k。
那么,我们可以预处理出 5 × 1 0 4 5\times 10^4 5×104以内的所有质数,用这些质数即可判断 2 × 1 0 9 2\times 10^9 2×109以内的每个数是不是质数。若枚举每两个数来判断是不是质数,则时间复杂度是 O ( n 2 P ) O(n^2P) O(n2P)的(其中 P P P为 5 × 1 0 4 5\times 10^4 5×104以内的质数个数, P = 5133 P=5133 P=5133)。
我们考虑优化。对于每个质数 p p p,令 b i = a i % p b_i=a_i\% p bi=ai%p,然后将 b i b_i bi排序,那么此时 b i b_i bi由若干个值相同的部分组成。假设有一部分的值都为 x x x,则我们需要找到值都为 p − x p-x p−x的部分,则枚举这两部分的 a a a值。设第一部分枚举到 a i a_i ai,第二部分枚举到 a j a_j aj,则如果 a i + a j > p a_i+a_j>p ai+aj>p,则 a i + a j a_i+a_j ai+aj一定是 p p p的若干倍,那么其一定是合数,做一个标记。
你可能会问:对于每个质数,最多有可能标记 n 2 n^2 n2次,那时间复杂度不还是 O ( n 2 P ) O(n^2P) O(n2P)吗?
对于每个 a i + a j a_i+a_j ai+aj,它只会被它的质因数打标记,而 a i + a j a_i+a_j ai+aj的质因数最多为 log ( a i + a j ) \log(a_i+a_j) log(ai+aj)个,所以平摊下来,时间复杂度为 O ( n 2 log v ) O(n^2\log v) O(n2logv),其中 v v v为 a i + a j a_i+a_j ai+aj的最大值。枚举的时间复杂度为 O ( n P ) O(nP) O(nP),所以这部分的时间复杂度为 O ( n 2 log v + n P ) O(n^2\log v+nP) O(n2logv+nP)。
当然,也可以用用 Miller-Rabin \text{Miller-Rabin} Miller-Rabin算法来判断 a i + a j a_i+a_j ai+aj是不是质数。
知道了每两个数之和是否为质数之后,我们建一个图,对于和为质数的两个数,我们将这两个数在图上对应的点连一条边,那么题意就是求最大点独立集。
我们观察图的性质。
如果组成的质数为偶质数,那么这个质数一定为 2 2 2,组成它的两个 a a a值一定都为 1 1 1。也就是说,在所有 a i a_i ai中只保留最多一个 1 1 1,即可保证不会出现偶质数。这个在输入的时候特殊处理一下即可。
那么, a i + a j a_i+a_j ai+aj为质数的话,只可能为奇质数,那么 a i a_i ai和 a j a_j aj的奇偶性一定不同。于是,上面的图就是一个二分图了。二分图的最大点独立集等于二分图的顶点数减去二分图的最大匹配数,那我们只需要求这个二分图的最大匹配即可。
这个二分图的点数为 n n n,边数为 m = n 2 m=n^2 m=n2。我们可以用匈牙利算法来求二分图的最大匹配,时间复杂度为 O ( n m ) O(nm) O(nm),即 O ( n 3 ) O(n^3) O(n3)。感觉会 TLE \text{TLE} TLE,但是匈牙利的时间复杂度为点数乘边数。设左边的点数为 x x x,则最坏情况下要做的次数为 n ⋅ x ( n − x ) n\cdot x(n-x) n⋅x(n−x),最大值为 n 3 4 \dfrac{n^3}{4} 4n3,而这是跑不满的。所以用匈牙利算法是可行的。
当然,也可以用 Dinic \text{Dinic} Dinic算法来求二分图的最大匹配,时间复杂度为 O ( n m ) O(n\sqrt m) O(nm),即 O ( n 2 ) O(n^2) O(n2)。
求完最大匹配之后,用点数减去最大匹配即可得到这个图的最大点独立集,也就是答案。
时间复杂度为 O ( ∑ ( n 2 log v + n P + n 3 ) ) O(\sum(n^2\log v+nP+n^3)) O(∑(n2logv+nP+n3)),其中 n 3 n^3 n3是带一个 1 4 \dfrac 14 41的常数的,而且这跑不满,时限还给了 2000 m s 2000ms 2000ms,所以这是可以过的。
code
#include<bits/stdc++.h>
using namespace std;
const int N=750,P=50000;
int T,n,p1,p2,q1,q2,ans,a[N+5],p[P+5],z[P+5],gt[N+5],t[N+5][N+5];
int tot,d[2*N*N+5],l[2*N*N+5],r[N+5],cx[N+5],cy[N+5];
struct node{int x,id;
}b[N+5];
bool cmp(node ax,node bx){return ax.x<bx.x;
}
void add(int xx,int yy){l[++tot]=r[xx];d[tot]=yy;r[xx]=tot;
}
void init(){for(int i=2;i<=P;i++){if(!z[i]) p[++p[0]]=i;for(int j=1;j<=p[0]&&i*p[j]<=P;j++){z[i*p[j]]=1;if(i%p[j]==0) break;}}
}
int dfs(int u){for(int i=r[u];i;i=l[i]){if(gt[d[i]]) continue;gt[d[i]]=1;if(!cy[d[i]]||dfs(cy[d[i]])){cx[u]=d[i];cy[d[i]]=u;return 1;}}return 0;
}
int main()
{
// freopen("cooking.in","r",stdin);
// freopen("cooking.out","w",stdout);init();scanf("%d",&T);while(T--){scanf("%d",&n);tot=0;memset(r,0,sizeof(r));memset(t,0,sizeof(t));for(int i=1,bz=0;i<=n;i++){scanf("%d",&a[i]);if(a[i]==1){if(!bz) bz=1;else{--i;--n;continue;}}t[i][i]=1;}for(int nw=1;nw<=p[0];nw++){for(int i=1;i<=n;i++) b[i]=(node){a[i]%p[nw],i};sort(b+1,b+n+1,cmp);p1=p2=1;q1=q2=n;for(;p2<=n&&b[p2].x==0;p2++){for(int i=p1;i<=p2;i++){int w1=b[i].id,w2=b[p2].id;t[w1][w2]=t[w2][w1]=1;}}--p2;p1=p2+1;for(;;p1=p2+1,q1=q2-1){while(p1<=n&&q1>=1&&b[p1].x+b[q1].x!=p[nw]){if(b[p1].x+b[q1].x<p[nw]) ++p1;else --q1;}if(p1>n||q1<1||p1>q1) break;p2=p1;q2=q1;while(p2+1<=n&&b[p2+1].x==b[p1].x) ++p2;while(q2-1>=1&&b[q2-1].x==b[q1].x) --q2;for(int i=p1;i<=p2;i++){for(int j=q2;j<=q1;j++){int w1=b[i].id,w2=b[j].id;if(a[w1]+a[w2]>p[nw]) t[w1][w2]=t[w2][w1]=1;}}}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(!t[i][j]) add(i,j);}}ans=n;memset(cx,0,sizeof(cx));memset(cy,0,sizeof(cy));for(int i=1;i<=n;i++){if(a[i]%2==0) continue;if(!cx[i]){memset(gt,0,sizeof(gt));ans-=dfs(i);}}printf("%d\n",ans);}return 0;
}
相关文章:

2023NOIP A层联测17 黑暗料理
题目大意 给出一个长度为 n n n的序列 a i a_i ai,要求删去若干个数,使得剩下的数中任意两个数都不是质数。在满足条件的情况下最多能保留几个数。 有 T T T组数据。 1 ≤ T ≤ 4 , 1 ≤ n ≤ 750 , 1 ≤ a i ≤ 1 0 9 1\leq T\leq 4,1\leq n\leq 75…...

关于nacos的配置获取失败及服务发现问题的排坑记录
nacos配置更新未能获取到导致启动报错 排查思路: 1、是否添加了nacos的启动pom依赖 参考: <dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-starter-alibaba-nacos-config</artifactId><…...
【QT】其他常用控件1
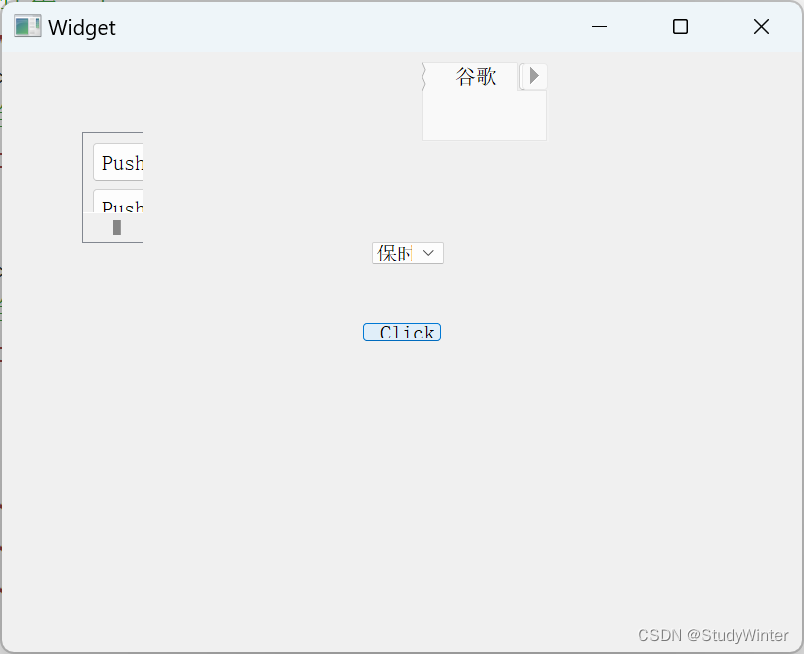
新建项目 scrollArea 滚动 toolBox 插入 tabWidget stackedWidget 切换 索引是0 运行后,没有切换按钮,结合pushbutton,加两个Button 代码 #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent)…...
交换机/防火墙-基础配置-23.10.11
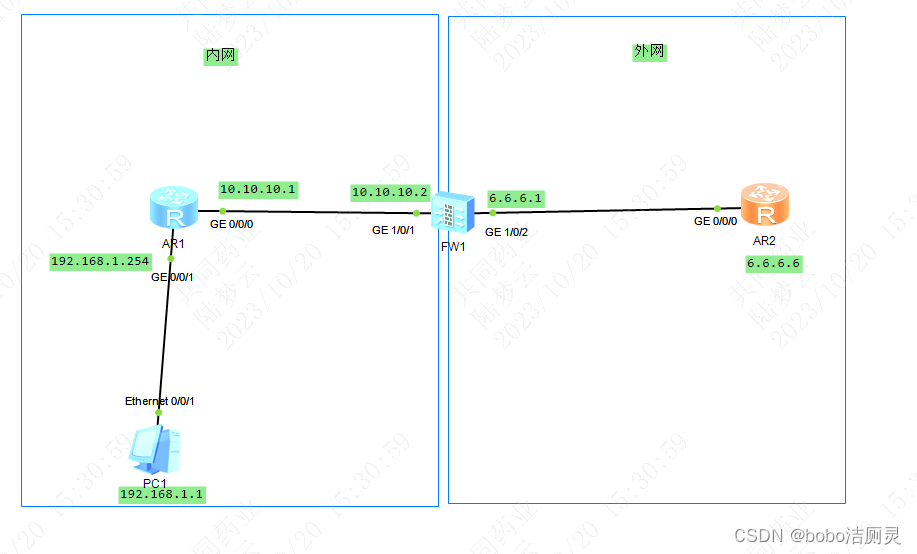
update 优化了目录逻辑 -10.24.2023 一.前置知识 1.MAC地址 交换机在给主机之间传递信息包时,通过MAC地址来标识每台主机 主机间发生信息包交换时,交换机就会将通信过的主机的mac地址存下 dis mac-address 交换机转发的数据包中,会包含一…...
-- Json字符 与 JsonObject 的相互转化)
alibaba.fastjson的使用(四)-- Json字符 与 JsonObject 的相互转化
目录 1. Json字符串转JsonObject 2. JsonObject转Json字符串 1. Json字符串转JsonObject 使用到的方法1: static JSONObject parseObject(String text) 使用到的方法2: public String getString(String key) /*** 将Json字符串转为JsonObject对象* 取值不存在时,返回null…...

linux 主机通信 ipv6 配置
1.检查系统内核是否支持IPv6协议: 在Linux控制台中运行下列命令: cat /proc/sys/net/ipv6/conf/all/disable_ipv6如果返回结果是0,就表明系统支持IPv6协议;若是1,则表明系统目前不支持IPv6协议; 2.禁用I…...
【JavaEE】初识计算机网络(TCP/IP五层模型及封装和分用)
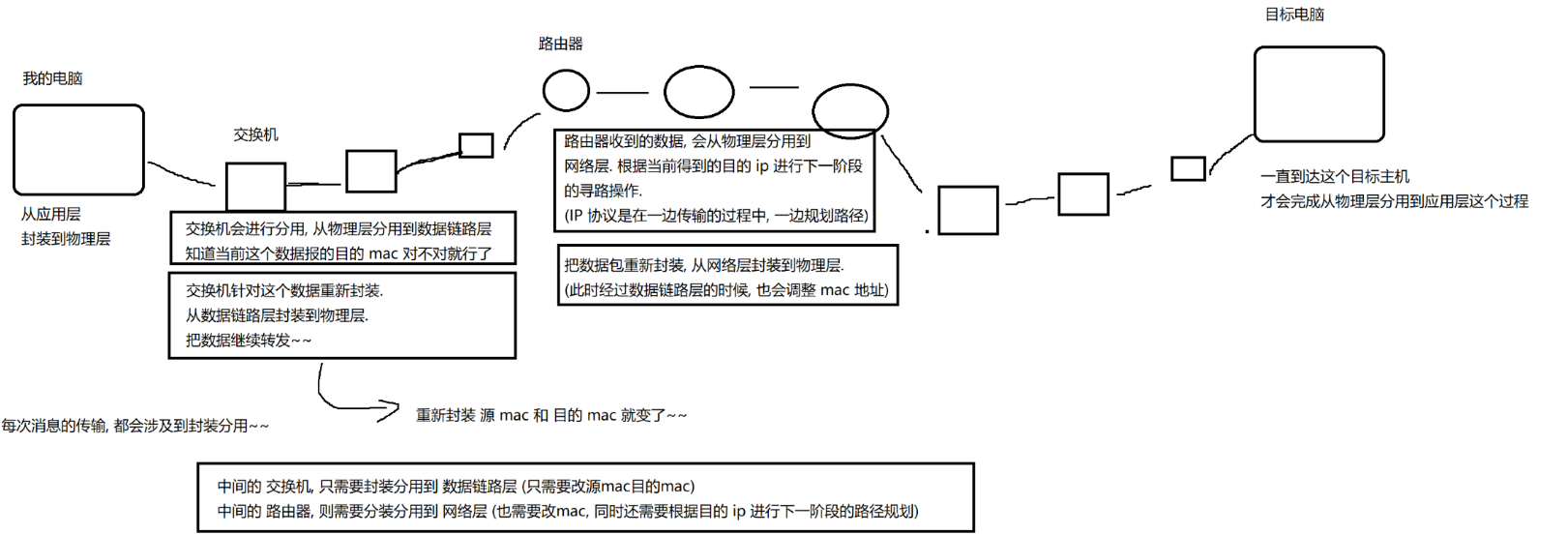
一、 网络通信基础 网络互连的目的是进行网络通信,也即是网络数据传输,更具体一点,是网络主机中的不同进程间,基于网络传输数据。 那么,在组建的网络中,如何判断到底是从哪台主机,将数据传输到…...

在nodejs中实现实时通信的几种方式
在nodejs中实现实时通信的几种方式 在当今世界中,实时通信至关重要。无论是聊天应用程序还是实时体育更新,实时通信都是保持用户活跃度所必需的。Node.js 因其速度、可扩展性和可靠性而成为开发实时应用程序的流行工具。在本文中,我们将探讨…...
【tg】 7 GroupInstanceCustomImpl
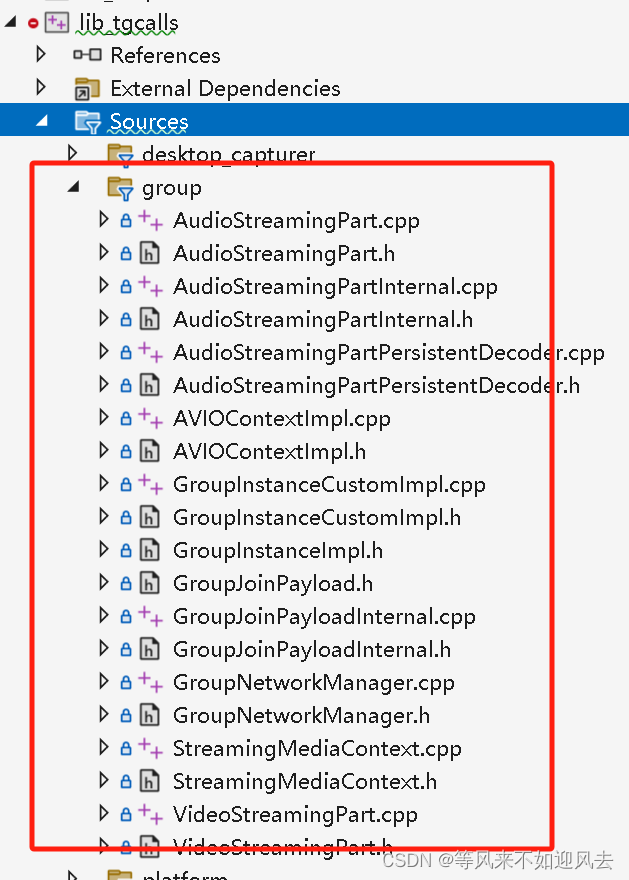
group GroupInstanceCustomImpl 核心GroupInstanceCustomInternal G:\CDN\P2P-DEV\tdesktop-offical\Telegram\ThirdParty\tgcalls\tgcalls\group\GroupInstanceCustomImpl.h 最核心是是GroupInstanceCustomInternal: private:std::shared_ptr<Threads> _threads;std::u…...
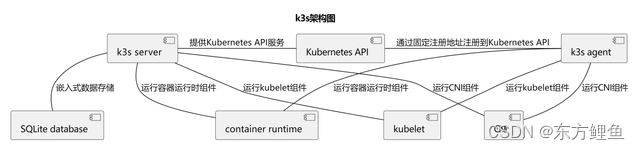
kubernates 集群实战-安装K3s集群
安装K3s集群 安装K3s集群环境准备安装 docker主节点安装work 节点验证环境 安装K3s集群 K3S是一种轻量级的Kubernetes发行版,安装和运行只需要一个二进制文件。相比之下,K8S需要更多的步骤和资源来安装和部署,例如设置etcd集群、安装控制平面…...
通俗介绍:什么是 Redis ?
刚接触 Redis 的伙伴们可能会因为不熟悉而感到困惑。本文简述 Redis 是什么、有哪些作用的问题,是一篇短浅而入门级别的文章。 Redis官网:Redis 打开 Redis 官网可以看到,官方对 Redis 的介绍是这样的:The open source, in-memo…...
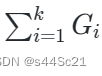
蓝桥算法赛(摆玩具)
问题描述 小蓝是一个热爱收集玩具的小伙子,他拥有 n 个不同的玩具。 这天,他把 n 个玩具按照高度顺序从矮到高摆放在了窗台上,然后,他希望将这些玩具分成 k 个段,使得所有分段的极差之和尽可能小。 具体来说&…...
vueDay04——v-if else show
一、v-if的使用 我们可以像c语言一样去使用v-if结构 比如单用v-if,连用v-if v-else,或者是v-if v-else-if v-else 注意: 1.v-if v-else-if需要绑定值,而v-else不需要绑定值 2.if结构可以用在不同的标签类型之间 <div v-if"fir…...

大数据技术学习笔记(二)—— Hadoop 运行环境的搭建
目录 1 准备模版虚拟机hadoop1001.1 修改主机名1.2 修改hosts文件1.3 修改IP地址1.3.1 查看网络IP和网关1.3.2 修改IP地址 1.4 关闭防火墙1.5 创建普通用户1.6 创建所需目录1.7 卸载虚拟机自带的open JDK1.8 重启虚拟机 2 克隆虚拟机3 在hadoop101上安装JDK3.1 传输安装包并解压…...
002——GO两数相加)
leetcode系列(双语)002——GO两数相加
文章目录 两数相加 | Add Two Numbers示例个人解答官方解答扩展Algorithm 两数相加 | Add Two Numbers You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a sing…...

废柴勇士(据说没有人能坚持37秒)
欢迎来到程序小院 废柴勇士 玩法:点击屏幕下方左右按键击杀怪物,怪物会在左右方向同时来袭,快速点击按钮进行击杀怪物,看您能够坚持多少秒, 据说还没有能够坚持37秒,快去击杀怪物挑战吧^^。开始游戏https:…...
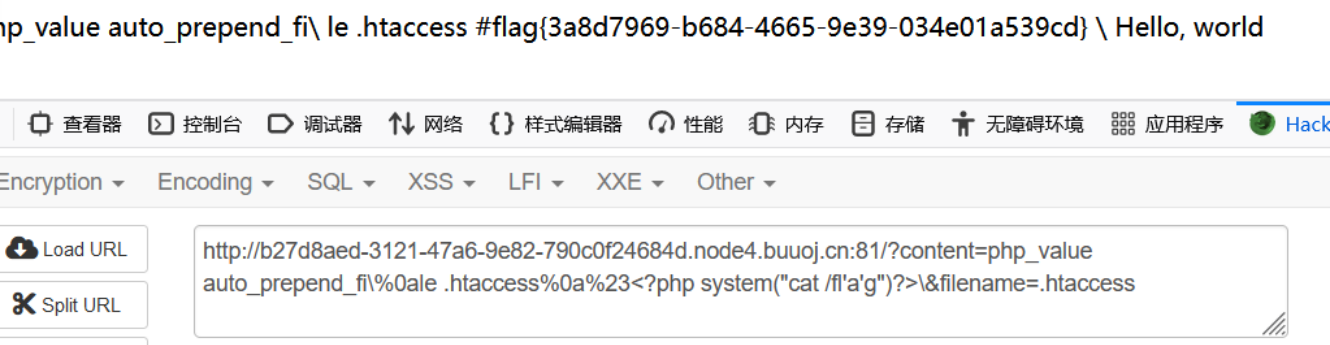
buuctf_练[羊城杯2020]easyphp
[羊城杯2020]easyphp 文章目录 [羊城杯2020]easyphp掌握知识解题思路关键paylaod 掌握知识 .htaccess文件的利用,把自己指定当做 php文件处理;preg_match正则匹配的了解,stristr函数的绕过;file_put_contents文件写入操作的了…...

【Linux】安装配置虚拟机及虚拟机操作系统的安装
目录 一、操作系统 1. 介绍 2. 功能 3. 有哪些 4. 个人版本和服务器版本的区别 二、VMWare虚拟机 1. 安装 2. 配置 三、安装配置Windows Server 1. 配置 2. 安装 四、虚拟机的环境配置及连接 1. 主机连接虚拟机 2. 虚拟机环境配置及共享 3. 环境配置 一、操作系…...
hugo-stack for github
静态博客框架jekyll、hexo和hugo三者之间的区别与差异 博客生成器? 全名为静态网站生成器, 可在任意拥有主机功能的环境下寄存(托管)可直接配合域名进行全球访问 劣势: 每次更新网页必须重新生成整个网站编译速度(单位:秒) Jek…...

【uniapp】proxy 代理切换至线上测试地址调试接口
本地测试地址形如:http://192.168.124.x:xxxx 线上测试地址形如:https://xxxx.xxxx.com 使用线上地址之后需要修改配置项 secure 为 true const constant require(./src/utils/constant) module.exports {devServer: {proxy: {/api: {target: constan…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...

【Zephyr 系列 8】构建完整 BLE 产品架构:状态机 + AT 命令 + 双通道通信实战
🧠关键词:Zephyr、BLE、状态机、双向透传、AT 命令、Buffer、主从共存、系统架构 📌适合人群:希望开发 BLE 产品(模块/标签/终端)具备可控、可测、可维护架构的开发者 🧭 引言:从“点功能”到“系统架构” 前面几篇我们已经逐步构建了 BLE 广播、连接、数据透传系统…...
