初始化固定长度的数组
完全解析Array.apply(null,「length: 1000」)
创建固定长度数组,并且初始化值。直接可以使用map、forEach、reduce等有遍历性质的方法。
如果直接使用Array(81),map里面的循环不会执行。
//方法一
Array.apply(null, { length: 20 })//方法二
Array(81).fill(null)<script setup lang='ts'>import { ref } from 'vue'let list = ref(Array(81).fill(null).map((_,index)=>{return {id:index,number:(index%9)}}))console.log(list)
</script>相关文章:

初始化固定长度的数组
完全解析Array.apply(null,「length: 1000」) 创建固定长度数组,并且初始化值。直接可以使用map、forEach、reduce等有遍历性质的方法。 如果直接使用Array(81),map里面的循环不会执行。 //方法一 Array.apply(null, { length: 20 })//方法二 Array(81)…...
实现基于 Jenkins 的多服务器打包方案
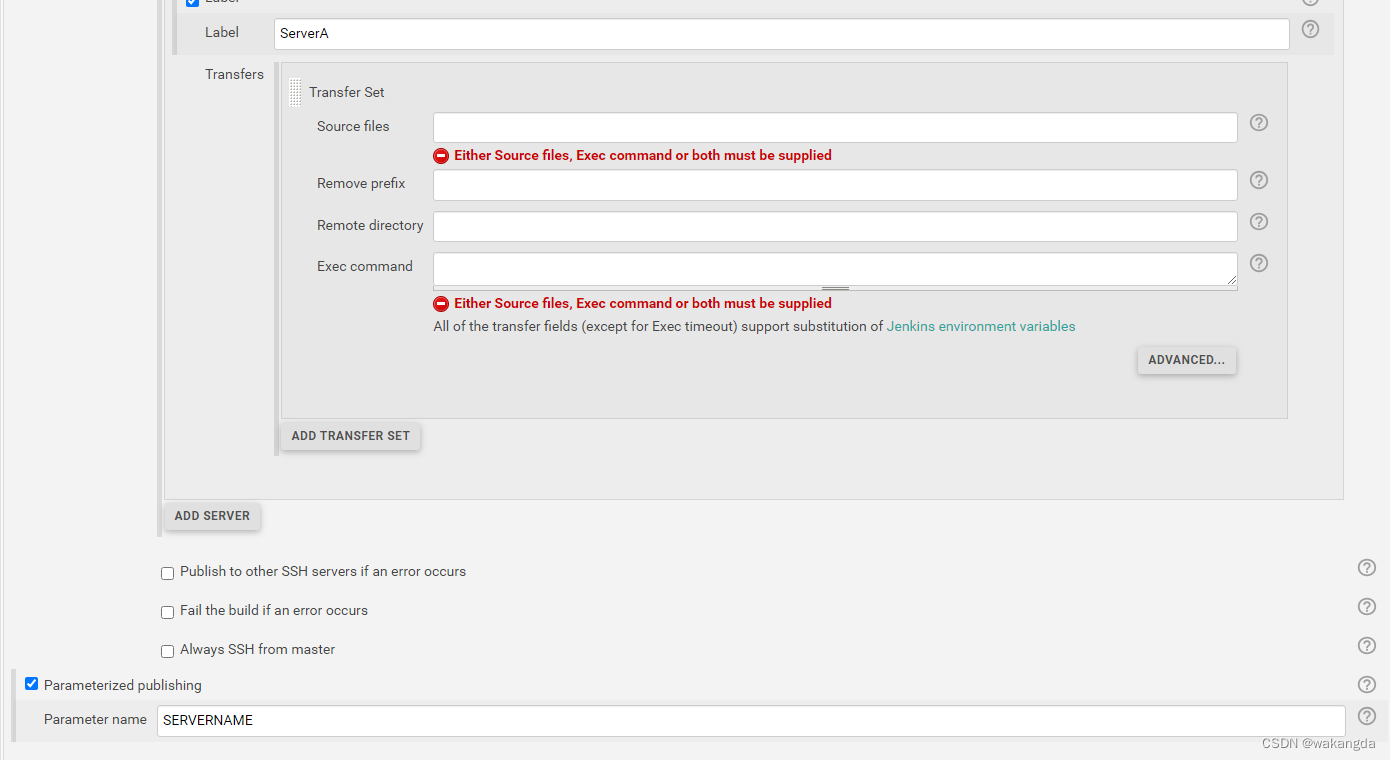
实现基于 Jenkins 的多服务器打包方案 在实际项目中,我们经常会遇到需要将一个应用程序或服务部署到不同的服务器上的需求。而使用 Jenkins 可以很方便地自动化这个过程。 设置参数 首先,我们需要设置一些参数,以便在构建过程中指定要部署…...

探索现代IT岗位:职业机遇的海洋
目录 1 引言2 传统软件开发3 数据分析与人工智能4 网络与系统管理5 信息安全6 新兴技术领域 1 引言 随着现代科技的迅猛发展,信息技术(IT)行业已经成为了全球经济的关键引擎,改变了我们的生活方式、商业模式和社会互动方式。IT行…...

np.linspace精确度
前言 今天发现一个大坑,如果是序列是小数的话,不要用np.linspace,而要用np.arrange指定等差序列。比如入下图中a和b是一样的意思,但是b是有较大误差的。 anp.arange(0,4,0.4) bnp.linspace(0,4,10) print("a",a) prin…...

GD32_定时器输入捕获波形频率
GD32_定时器输入捕获波形频率(多通道轮询) 之前项目上用到一个使用定时器捕获输入采集风扇波形频率得到风扇转速的模块,作为笔记简单记录以下当时的逻辑结构和遇到的问题,有需要参考源码、有疑问或需要提供帮助的可以留言告知 。…...

单窗口单IP适合炉石传说游戏么?
游戏道具制作在炉石传说中是一个很有挑战的任务,但与此同时,它也是一个充满机遇的领域。在这篇文章中,我们将向您展示如何在炉石传说游戏中使用动态包机、多窗口IP工具和动态IP进行游戏道具制作。 作者与主题的关系:作为一名热爱炉…...
win11安装docekr、docker-compose
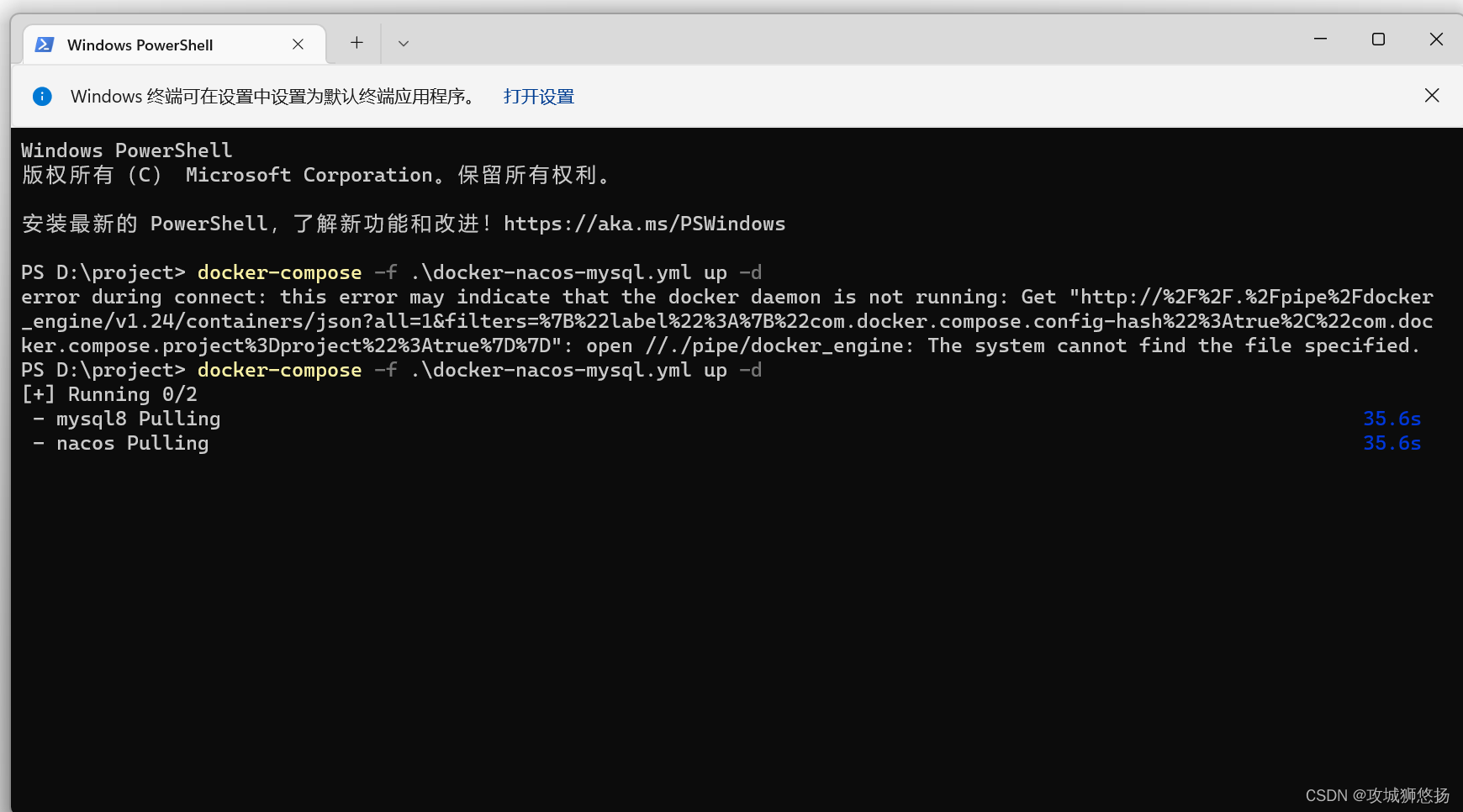
1.docker安装 下载地址:Install Docker Desktop on Windows | Docker Docs 出问题别慌,看清楚提示信息,cmd更新wsl,什么是wsl,百度好好理解一下哦 2.docker-compose安装 还是去官方看看怎么说的,然后跟着处…...
Postman的简单使用
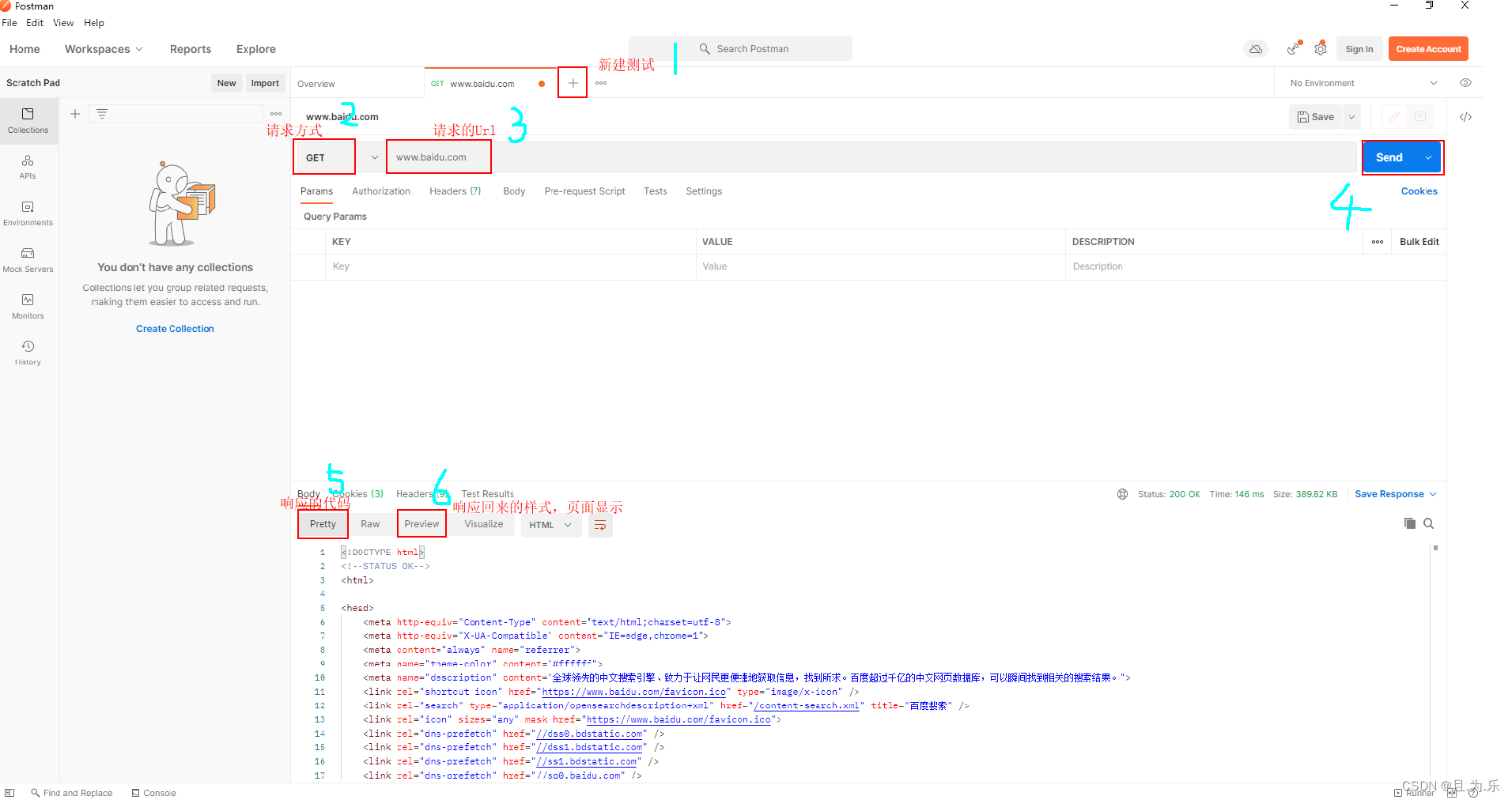
Postman简介 官网 Postman是Google公司开发的一款功能强大的网页调试与发送HTTP请求,并能运行测试用例的Chrome插件 使用Postman进行简单接口测试 新建测试 → 选择请求方式 → 请求URL,下面用百度作为例子: 参考文档 [1] Postman使用教程…...
信号继电器驱动芯片(led驱动芯片)
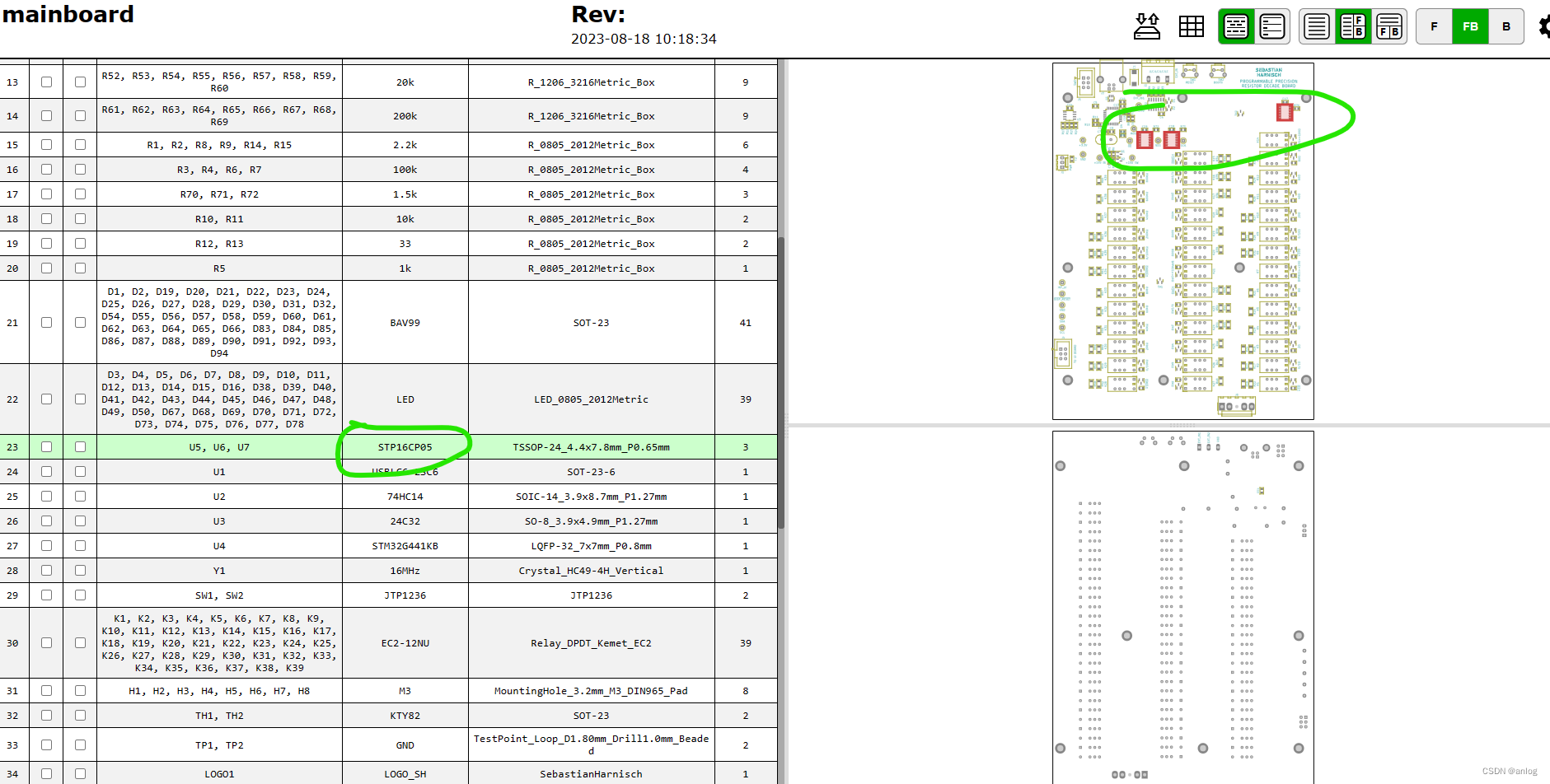
驱动继电器需要配合BAV99(防止反向脉冲)使用 具体应用参考开源项目 电阻箱 sbstnh/programmable_precision_resistor: A SCPI programmable precision resistor (github.com) 这个是芯片的输出电流设置 对应到上面的实际开源项目其设置电阻为1.5K&…...
IDEA配置HTML和Thymeleaf热部署开发
IDEA配置HTML和Thymeleaf热部署开发 1.项目配置2. IDEA配置3. 使用 需求:现在我们在开发不分离项目的时候(SpringBootThmeleaf)经常会改动了类或者静态html文件就需要重启一下服务器, 这样不仅时间开销很大,而且经常重…...
Nginx动静分离
为了加快网站的解析速度,可以把动态页面和静态页面由不同的服务器来解析,加快解析速度。降低原来单个服务器的压力。 在动静分离的tomcat的时候比较明显,因为tomcat解析静态很慢,其实这些原理的话都很好理解,简单来说&…...

Spring中AOP详解
目录 一、AOP的概念 二、AOP的底层实现原理 2.1 JDK的动态代理 2.1.1 invocationhandler接口 2.1.2 代理对象和原始类实现相同的接口 interfaces 2.1.3 类加载器ClassLoador 2.1.4 编码实现 2.2 Cglib动态代理 2.2.1 Cglib动态代理编码实现 三、AOP如何通过原始对象的id获取到代…...

Unity DOTS系列之Filter Baking Output与Prefab In Baking核心分析
最近DOTS发布了正式的版本, 我们来分享一下DOTS里面Baking核心机制,方便大家上手学习掌握Unity DOTS开发。今天给大家分享的Baking机制中的Filter Baking Output与Prefab In Baking。 对啦!这里有个游戏开发交流小组里面聚集了一帮热爱学习游戏的零基础…...

Matlab读写操作
随机生成一个3*3矩阵,对矩阵进行按列升序排列 >> Arand(3,3); >> [B, ~] sort(A, 2); >> B B 0.4898 0.6797 0.70940.4456 0.6551 0.75470.1626 0.2760 0.6463在不同数值类型下显示π的值 1、默认数值类型 >> p_defa…...
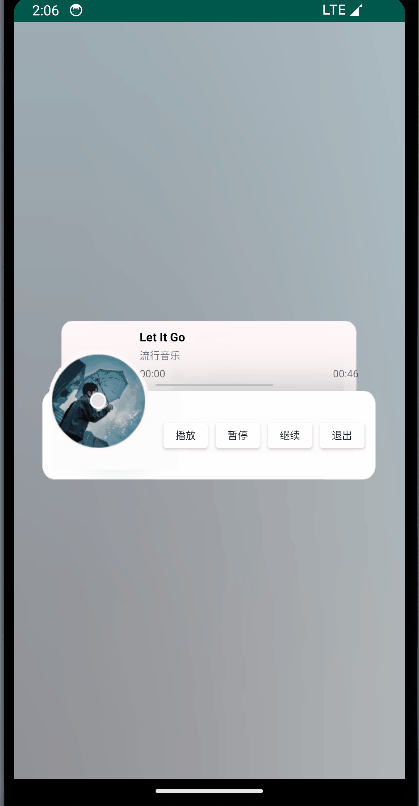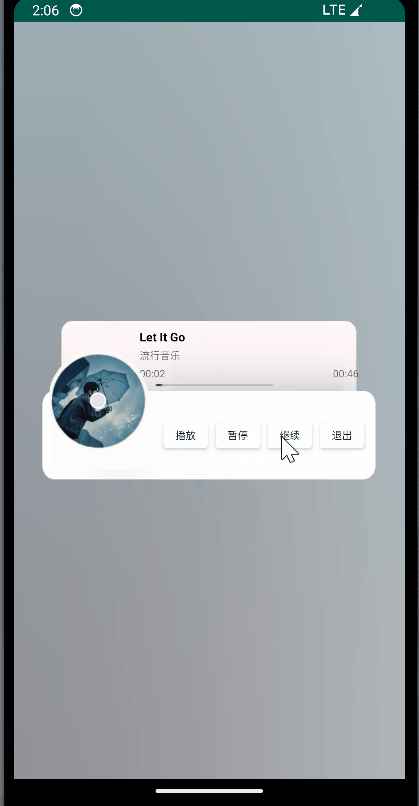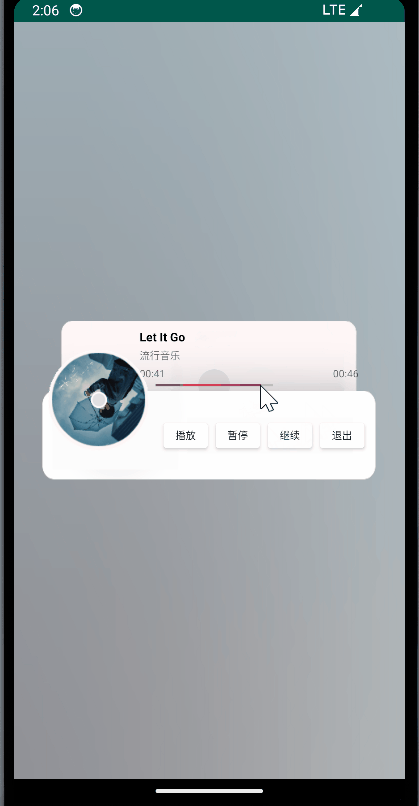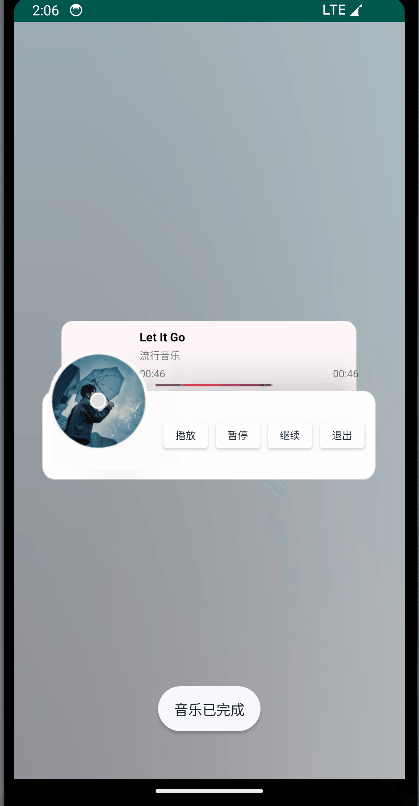
Android 开发技巧:音乐播放器的后台处理【Service、Handler、MediaPlayer】
给定部分完成的MusicPlayer项目,实现其中未完成的service部分: 1、创建MusicService类,通过service组件实现后台播放音乐的功能; 2、在MainActivity中通过ServiceConnection连接MusicService,实现对音乐播放的控制&…...

使用Windows平台的Hyper-V虚拟机安装CentOS7的详细过程
Hyper-V虚拟机安装CentOS7 前言常见Linux系统CentOSUbuntuDebianKaliFedoraArch LinuxMintManjaroopenSUSE Hyper-V开启Hyper-V打开Hyper-V Hyper-V的使用新建虚拟机开始安装分区配置开始安装 修改yum源为阿里源 前言 作为一名开发者,就服务器而言,接触最…...
某马机房预约系统 C++项目(二) 完结
8.4、查看机房 8.4.1、添加机房信息 根据案例,我们还是先在computerRoom.txt中直接添加点数据 //几机房 机器数量 1 20 2 50 3 1008.4.2、机房类创建 同样我们在头文件下新建一个computerRoom.h文件 添加如下代码: #pragma once #include<i…...
npm 安装到指定文件夹
创建一个文件夹,用vscode或者cmd打开, 执行 npm install --prefix ./ 路径 包名, npm install --prefix ./ 包名 , 就会将包安装在当前文件夹, 例如: npm install --prefix ./ -g oppo-minigame…...
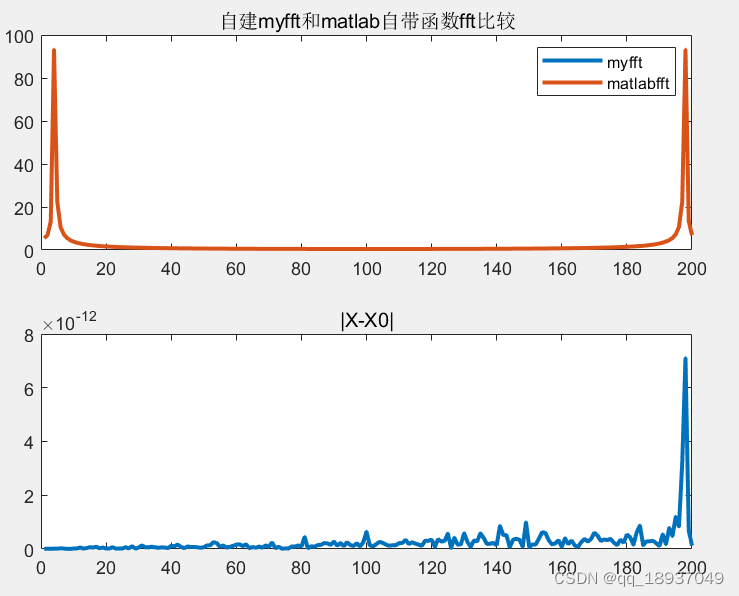
自建的离散傅里叶变换matlab程序实现及其与matlab自带函数比较举例
自建的离散傅里叶变换matlab程序实现及其与matlab自带函数比较举例 在matlab中有自带的离散傅里叶变换程序,即fft程序,但该程序是封装的,无法看到源码。为了比较清楚的了解matlab自带的实现过程,本文通过自建程序实现matlab程序&…...

Vue图片路径问题(动态引入)
vue项目中我们经常会遇到动态路径的图片无法显示的问题,以下是静态路径和动态路径的常见使用方法。 1.静态路径 在日常的开发中,图片的静态路径通过相对路径和绝对路径的方式引入。 相对路径:以.开头的,例如./、../之类的。就是…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
