【算法训练-动态规划 五】【二维DP问题】最大正方形
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【动态规划】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为:目标公司+最近一年+出现频率排序,由高到低的去牛客TOP101去找,只有两个地方都出现过才做这道题(CodeTop本身汇聚了LeetCode的来源),确保刷的题都是高频要面试考的题。
明确目标题后,附上题目链接,后期可以依据解题思路反复快速练习,题目按照题干的基本数据结构分类,且每个分类的第一篇必定是对基础数据结构的介绍。
最大正方形【MID】
来解决一道最大正方形的题目
题干
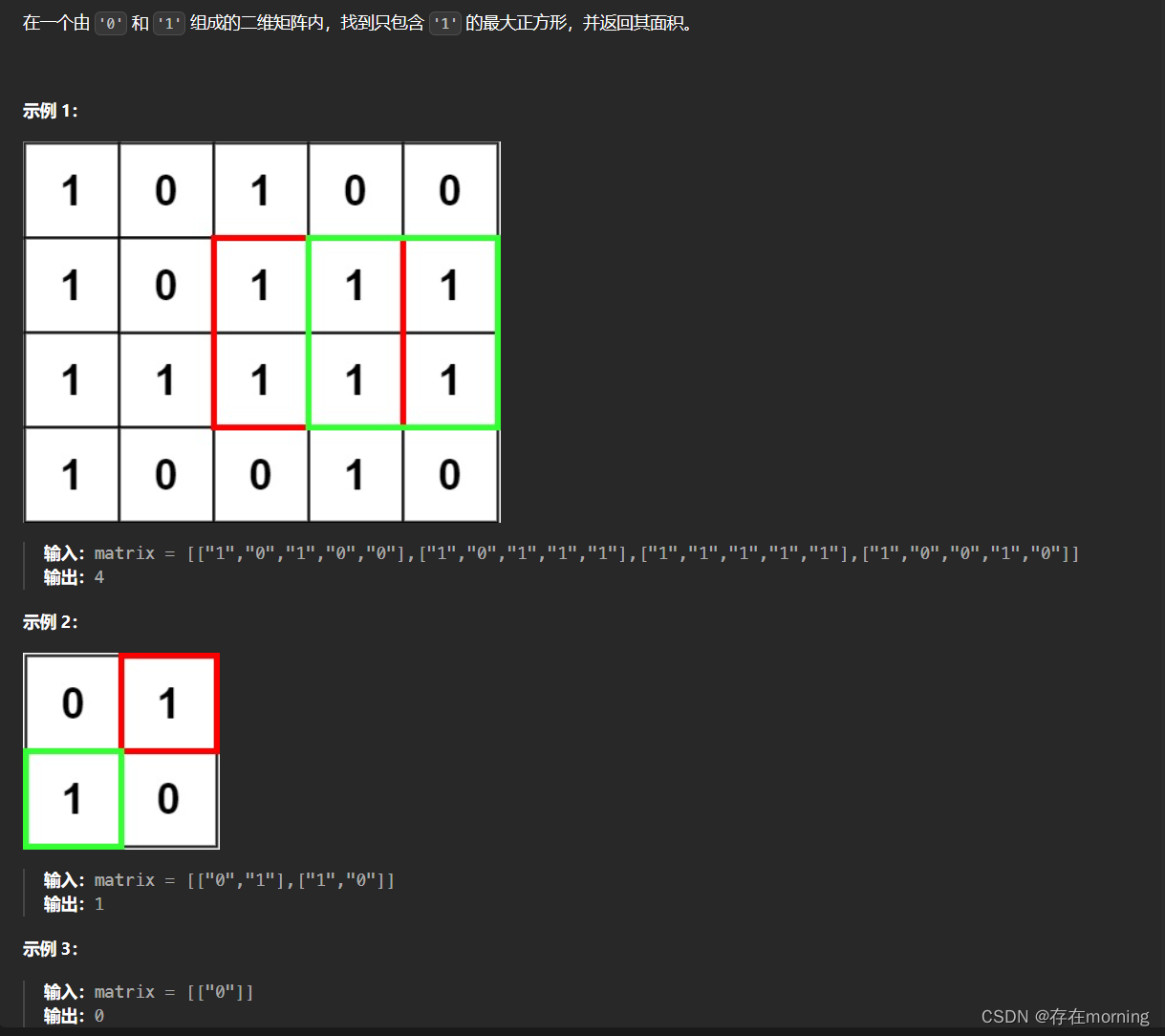
解题思路
原题解出处按照动态规划的标准解题讨论来进行解题,理解 min(上, 左, 左上) + 1,如题,在其他动态规划方法的题解中,大都会涉及到下列形式的代码:
// 伪代码
if (matrix(i , j ) == '1') {dp(i, j) = min(dp(i - 1, j), dp(i, j - 1), dp(i - 1, j - 1)) + 1;
}
其中,dp(i, j) 是以 matrix(i , j ) 为 右下角 的正方形的最大边长,
若某格子值为 1,则以此为右下角的正方形的、最大边长为:上面的正方形、左面的正方形或左上的正方形中,最小的那个,再加上此格
先来阐述简单共识
- 若形成正方形(非单 1),以当前为右下角的视角看,则需要:当前格、上、左、左上都是 1
- 可以换个角度:当前格、上、左、左上都不能受 0 的限制,才能成为正方形
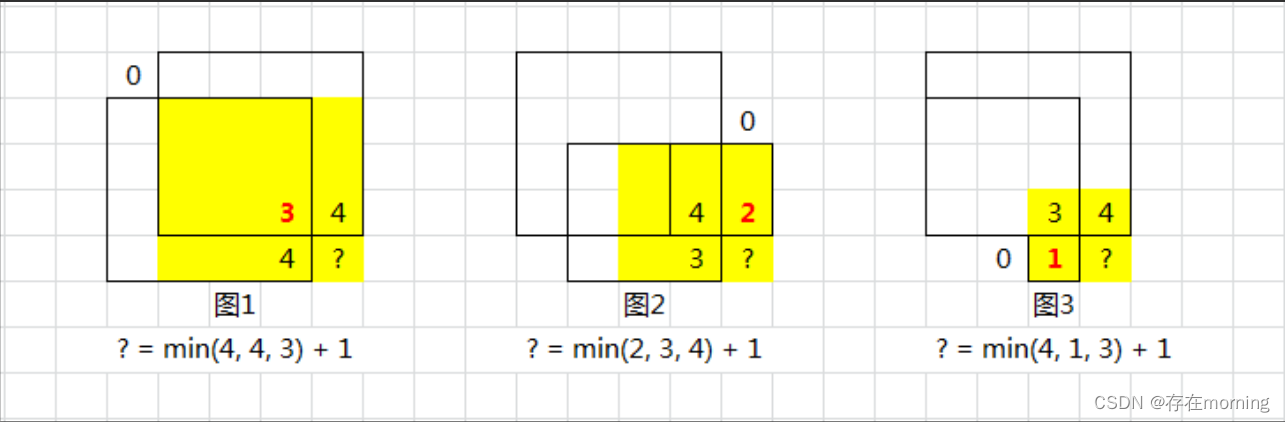
上面详解了 三者取最小 的含义:
- 图 1:受限于左上的 0
- 图 2:受限于上边的 0
- 图 3:受限于左边的 0
数字表示:以此为正方形右下角的最大边长;黄色表示:格子 ? 作为右下角的正方形区域。就像 木桶的短板理论 那样——附近的最小边长,才与 ? 的最长边长有关。 此时已可得到递推公式
// 伪代码
if (grid[i][j] == '1') {dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1;
}
1 定义状态(定义子问题)
dp 具体定义:dp[i ][j ] 表示 「以第 i 行、第 j 列为右下角的正方形的最大边长」
为何不是 dp[i][j],回到图解中,任何一个正方形,我们都「依赖」当前格 左、上、左上三个方格的情况,但第一行的上层已经没有格子,第一列左边已经没有格子,需要做特殊 if 判断来处理,为了代码简洁,我们 假设补充 了多一行全 ‘0’、多一列全 ‘0’
2 状态转移方程(描述子问题之间的联系)
取自己左上、上方、左边最小值再加上自身
// 伪代码
if (grid[i][j] == '1') {dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1;
}
3 初始化状态
初始值就是将第一列 dp[row][0] 、第一行 dp[0][col] 都赋为 0,相当于已经计算了所有的第一行、第一列的 dp 值
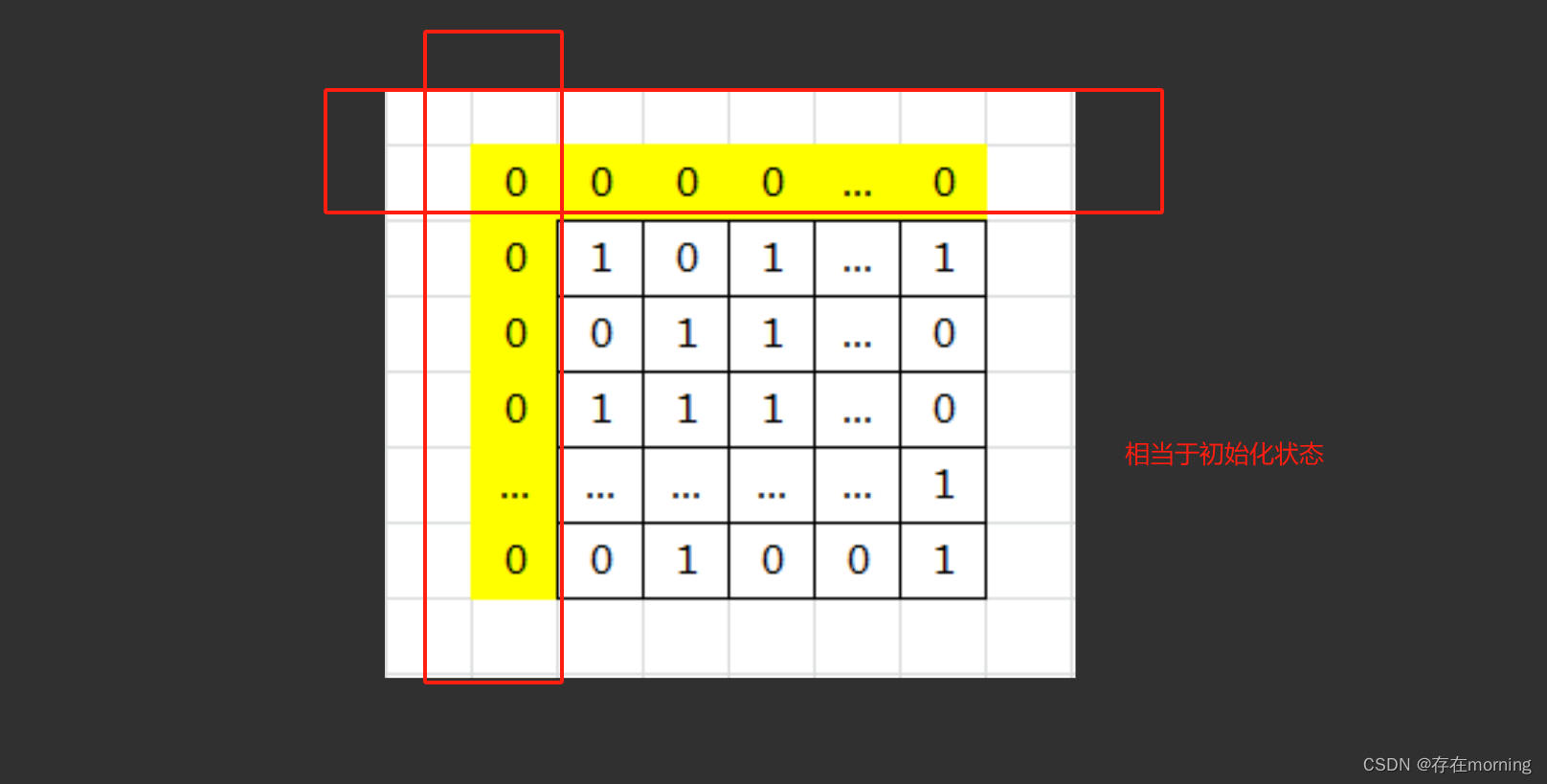
4 求解方向
这里采用自底向上,从最小的状态开始求解
5 找到最终解
题目要求面积。根据 「面积 = 边长 x 边长」可知,我们只需求出 最大边长 即可,定义 maxSide 表示最长边长,每次得出一个 dp,就 maxSide = max(maxSide, dp); 最终返回 return maxSide * maxSide;
代码实现
给出代码实现基本档案
基本数据结构:数组
辅助数据结构:无
算法:动态规划
技巧:无
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
当然包括但不限于以上
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param nums int整型一维数组* @return int整型一维数组*/public int maximalSquare(char[][] matrix) {// 1 入参校验if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {return 0;}// 2 定义最长边,以及获取边长int maxSide = 0;int row = matrix.length;int col = matrix[0].length;// 3 定义dp数组,dp[i][j]表示以i、j为坐标的元素作为右下角的最大正方形边长,默认初始化了两列0int[][] dp = new int[row + 1][col + 1];// 4 编写状态转移方程for (int i = 1; i <= row; i++) {for (int j = 1; j <= col; j++) {if (matrix[i - 1][j - 1] == '1') {dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;maxSide = Math.max(maxSide, dp[i][j]);}}}return maxSide * maxSide;}
}
考虑到每个方格都需要参与计算,双重循环要从索引1开始(否则dp[0][0]无法进行状态转移,会数组越界),这样为了第0行第0列可以参与计算,就给dp数组补了0,也就是base case,补0后dp的第1行和第1列对应的判断元素其实是matrix的第0行和第0列,所以这里的if条件是:matrix[i - 1][j - 1] == '1'
复杂度分析
时间复杂度:O(N^2),这里 N 是数组的长度,我们写了两个 for 循环,每个 for 循环的时间复杂度都是线性的;
空间复杂度:O(N),要使用和输入数组长度相等的状态数组,因此空间复杂度是 O(N)。
相关文章:

【算法训练-动态规划 五】【二维DP问题】最大正方形
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【动态规划】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…...

20.Node-Express框架的用法
题记 node.js中express框架的用法 Express框架的特点 可以设置中间件来响应 HTTP 请求。 定义了路由表用于执行不同的 HTTP 请求动作。 可以通过向模板传递参数来动态渲染 HTML 页面。 安装Express模块 npm install express --save 安装重要模块 npm install body-parser --…...

cuda卸载
去查看你的电脑显卡对应的cuda版本,不然还是一整个用不到gpu的情况嘿嘿. 啊啊啊啊打开控制面板看一下,驱动不要乱卸载: 这些东西不能全部卸载了哦,只能卸载含有“CUDA”的那几个(其实其他的可能也没有用 但是不懂的哇 …...
怎么选择好的游戏平台开发商?
选择好的游戏平台开发商需要考虑以下几个方面: 开发经验 了解游戏开发公司的历史和经验是找到靠谱公司的重要步骤。查看公司的官方网站、社交媒体账号等渠道,了解公司的发展历程、团队规模、客户案例等。同时,了解公司是否有相关的游戏开发经…...
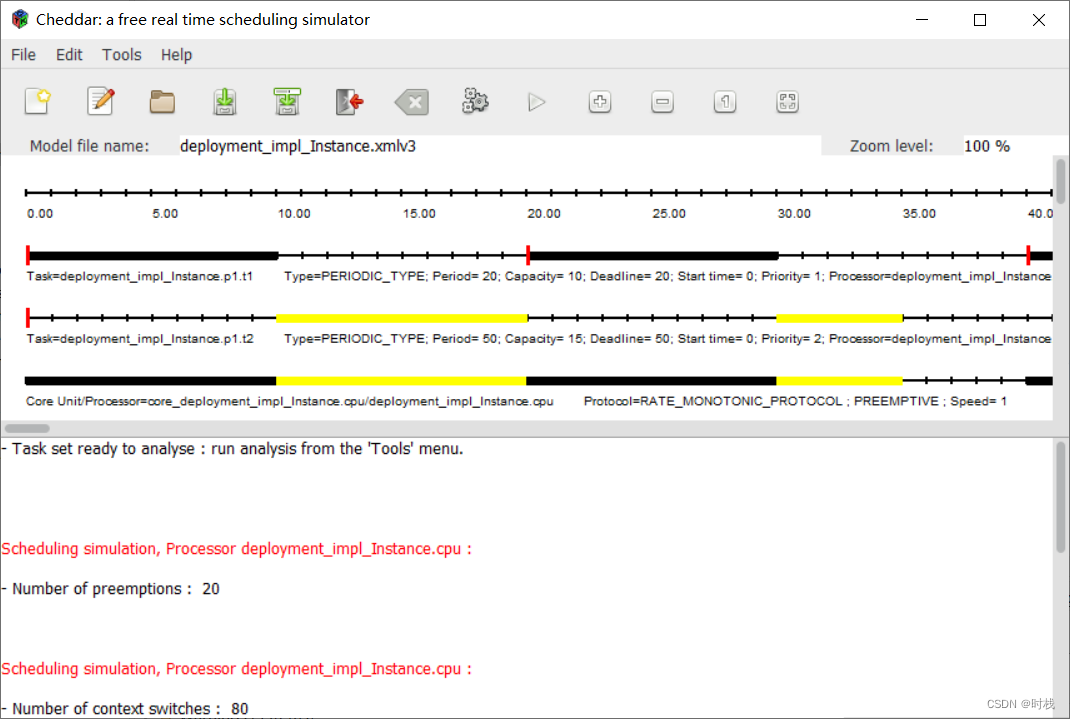
OSATE 插件 Cheddar 的安装与简单使用
一、Cheddar简介 Cheddar是一个开源的实时系统任务调度模拟器/分析仪,可以使用Cheddar进行任务的可调度性分析以及相关的性能分析。对于Cheddar的详细信息可以参考其官网: Cheddar - open-source real-time scheduling simulator/analyzer (univ-brest…...
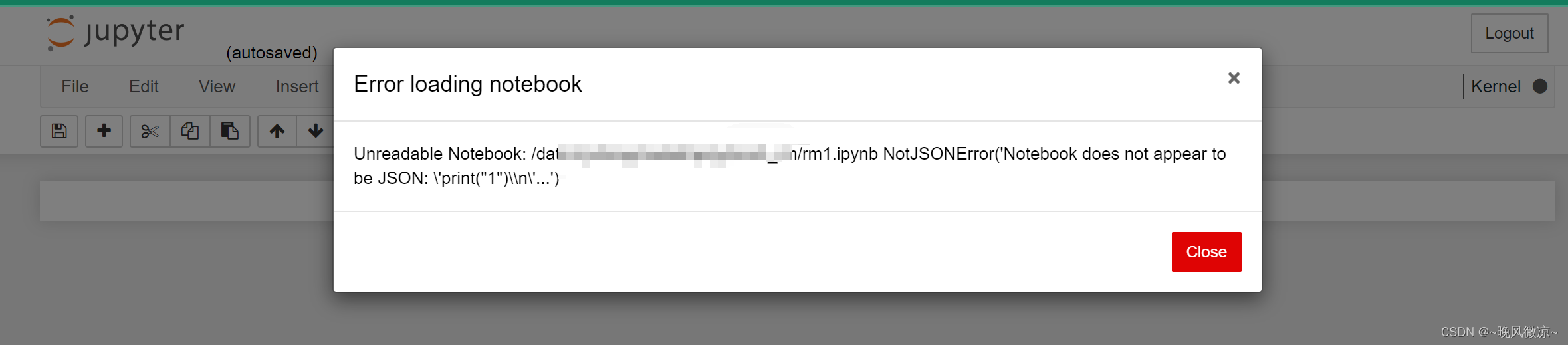
解决:vscode和jupyter远程连接无法创建、删除文件的问题(permission denied)
目录 问题:vscode和jupyter远程连接服务器无法创建、删除文件的问题原因:代码文件的权限不够解决方法:1.ls -l查看目录所在组,权限2.chown修改拥有者和所在组 问题:vscode和jupyter远程连接服务器无法创建、删除文件的…...

Android Studio模拟器/虚拟设备连接互联网的方法
如图,无线、网络都无法联网 找到本机的DNS 找到emu-launch-params.txt,添加DNS -dns-server 192.168.124.1 重启虚拟机,关闭无线...

linux 内存检测工具 kfence 详解
版本基于: Linux-5.10 约定: PAGE_SIZE:4K 内存架构:UMA 0. 前言 本文 kfence 之外的代码版本是基于 Linux5.10,最近需要将 kfence 移植到 Linux5.10 中,本文借此机会将 kfence 机制详细地记录一下。 k…...

虚拟机VMware Workstation Pro安装配置使用服务器系统ubuntu-22.04.3-live-server-amd64.iso
虚拟机里安装ubuntu-23.04-beta-desktop-amd64开启SSH(换源和备份)配置中文以及中文输入法等 一、获取Ubuntu服务器版 获取Ubuntu服务器版 二、配置虚拟机 选择Custom(advanced): 选择Workstation 17.x: 选择“I will install the operating system later.”…...
)
《C程序设计》笔记(ch1-2)
第1章 程序设计和C语言 1.2 什么是计算机语言 人和计算机都能识别的语言,就是计算机语言。 符号语言用一些英文字母和数字表示一个指令。汇编程序:符号语言的指令→机器指令。 编译程序:源程序→机器指令。 1.4 最简单的C语言程序 每一…...
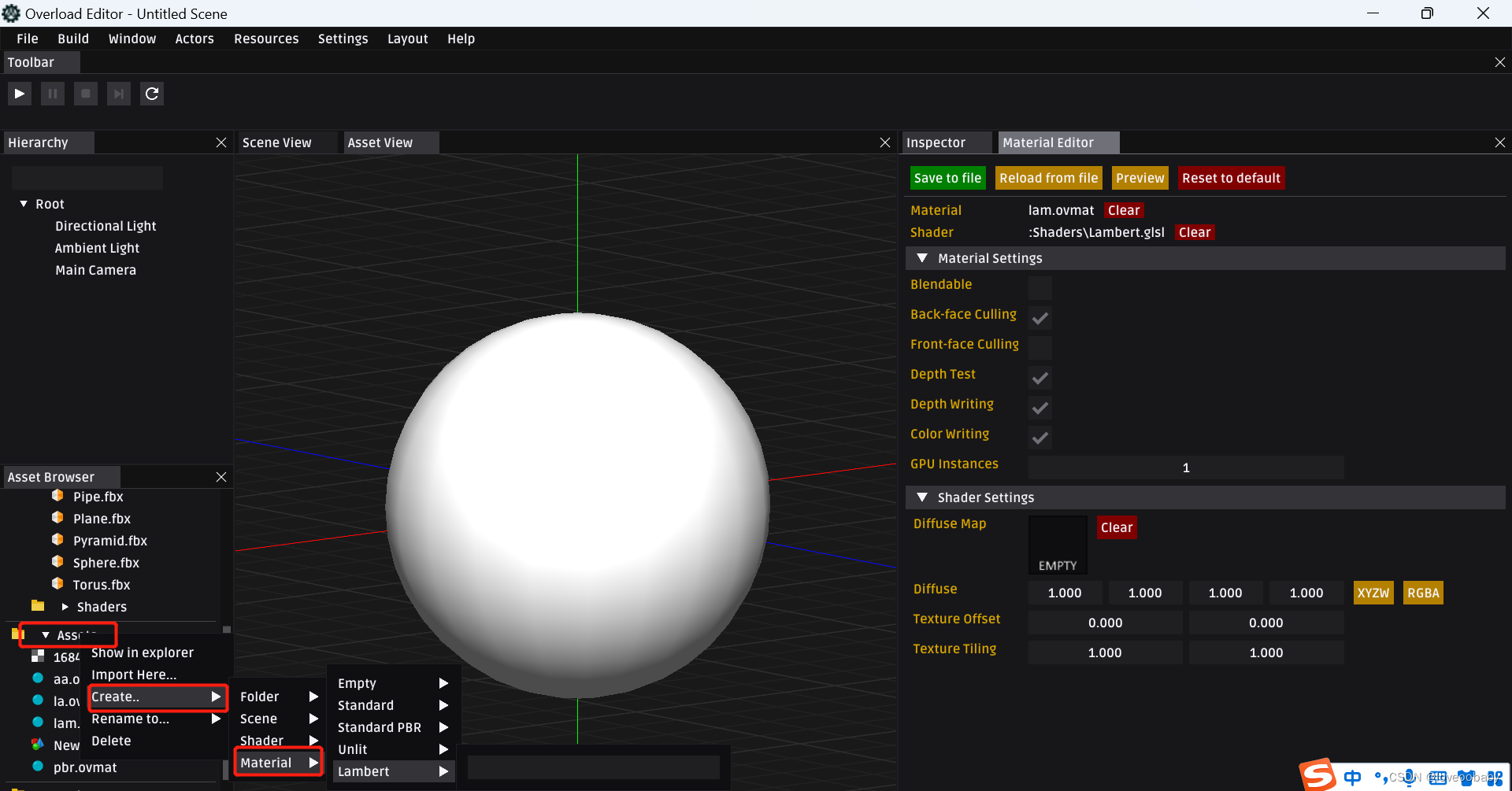
【Overload游戏引擎细节分析】Lambert材质Shader分析
一、经典光照模型:Phong模型 现实世界的光照是极其复杂的,而且会受到诸多因素的影响,这是以目前我们所拥有的处理能力无法模拟的。经典光照模型冯氏光照模型(Phong Lighting Model)通过单独计算光源成分得到综合光照效果,然后添加…...
二进制搭建 Kubernetes+部署网络组件+部署CornDNS+负载均衡部署+部署Dashboard
二进制搭建 Kubernetes v1.20 k8s集群master01:20.0.0.50 kube-apiserver kube-controller-manager kube-scheduler etcd k8s集群master02:20.0.0.100k8s集群node01:20.0.0.110 kubelet kube-proxy docker etcd k8s集群node02:20.…...
】)
【 OpenGauss源码学习 —— 列存储(update_pages_and_tuples_pgclass)】
列存储(update_pages_and_tuples_pgclass) 概述update_pages_and_tuples_pgclass 函数ReceivePageAndTuple 函数estimate_cstore_blocks 函数get_attavgwidth 函数get_typavgwidth 函数 vac_update_relstats 函数 测试案例 声明:本文的部分内…...
爬虫进阶-反爬破解7(逆向破解被加密数据:全方位了解字体渲染的全过程+字体文件的检查和数据查看+字体文件转换并实现网页内容还原+完美还原上百页的数据内容)
目录 一、全方位了解字体渲染的全过程 1.加载顺序 2.实践操作:浏览器中调试字体渲染 3.总结: 二、字体文件的检查和数据查看 1.字体文件的操作软件 2.映射关系的建立 3.实践操作:翻找样式和真实内容 4.总结: 三、字体文…...

系统架构设计师之RUP软件开发生命周期
系统架构设计师之RUP软件开发生命周期...
VM虚拟机 13.5 for Mac
VMware Fusion Pro for Mac是一款强大的虚拟机软件,可以在Mac操作系统中创建、运行和管理多个虚拟机,使用户可以在一台Mac电脑上同时运行多个操作系统和应用程序。 以下是VMware Fusion Pro for Mac的主要特点: 1. 支持多种操作系统ÿ…...

一篇教你学会Ansible
前言 Ansible首次发布于2012年,是一款基于Python开发的自动化运维工具,核心是通过ssh将命令发送执行,它可以帮助管理员在多服务器上进行配置管理和部署。它的工作形式依托模块实现,自己没有批量部署的能力。真正具备批量部署的是…...
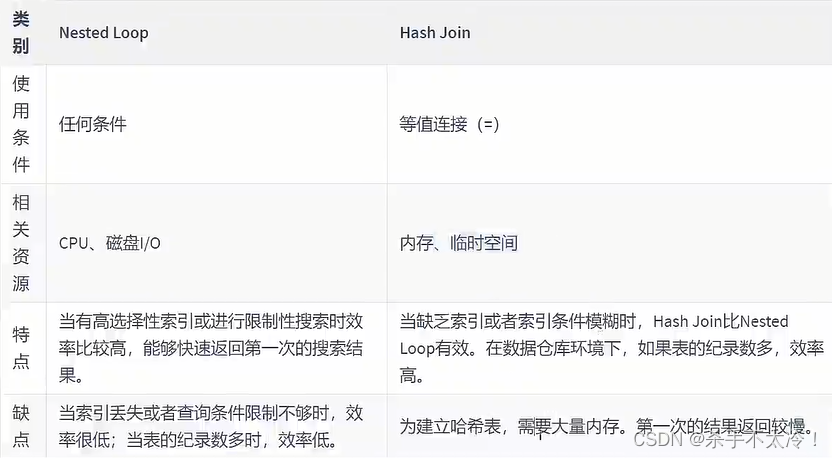
Mysql第四篇---数据库索引优化与查询优化
文章目录 数据库索引优化与查询优化索引失效案例数据准备1. 全值匹配2 最佳左前缀法则(联合索引)主键插入顺序4 计算、函数导致索引失效5 类型转换(自动或手动)导致索引失效6 范围条件右边的列索引失效7 不等于(!或者<>)索引失效8 is null可以使用索引, is not null无法使…...

SpringBoot手动获取实例
1.首先创建一个接口里面是关于建库建表的方法 public interface MetaMapper {//三个核心建表方法void createExchangeTable();void createQueueTable();void createBingdingTable(); } 2.启动类中定义一个ConfigurableApplicationContext 类型的变量context接收SpringApplica…...

栈(Stack)的概念+MyStack的实现+栈的应用
文章目录 栈(Stack)一、 栈的概念1.栈的方法2.源码分析 二、MyStack的实现1.MyStack的成员变量2.push方法3.isEmpty方法和pop方法4.peek方法 三、栈的应用1.将递归转化为循环1.调用递归打印2.通过栈逆序打印链表 栈(Stack) 一、 栈…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...

【Pandas】pandas DataFrame dropna
Pandas2.2 DataFrame Missing data handling 方法描述DataFrame.fillna([value, method, axis, …])用于填充 DataFrame 中的缺失值(NaN)DataFrame.backfill(*[, axis, inplace, …])用于**使用后向填充(即“下一个有效观测值”)…...

EC2安装WebRTC sdk-c环境、构建、编译
1、登录新的ec2实例,证书可以跟之前的实例用一个: ssh -v -i ~/Documents/cert/qa.pem ec2-user70.xxx.165.xxx 2、按照sdk-c demo中readme的描述开始安装环境: https://github.com/awslabs/amazon-kinesis-video-streams-webrtc-sdk-c 2…...
