Look Back(cf div3 905)
题意:给你一个长度为n((1≤n≤10^5)数组a[],你可以进行一个操作 使a[i]=a[i]*2,问最少经过多少次这样的操作使的a[]不递减,a[i]>=a[i-1]。
输入样例:
6
1
1
2
1 1
3
1 2 1
4
2 3 2 1
5
4 5 4 5 4
10
1 7 7 2 3 4 3 2 1 100
输出样例:
1 1 4 7 4 28
思路: 要想使它非递减,肯定使遇到a[i-1]>a[i] 便让a[i-1]*2^x>=a[i] 最少乘x次使得a[i-1]>=a[i]
但是要考虑一个问题:遇到一个这样的就让a[i-1]*2^x 相应的也会影响后面的数乘多少个2
如果都这样每一个暴力去乘去改变a[i-1]的值 N=1e5 数很大 若是最大可能 a[i]*2^N 会爆longlong
甚至会超时,这是就思考该怎么样去优化
采用前缀和的思想 用s[i]数组去计算 a[i]需要乘多少个2 不去实际改变a[i]的大小,而是用s[i]数组的方式记录下来每个数的达到符合要求的最小操作数
总的来说一共有两种情况
a[i]>=a[i-1]时
这时你要考虑 a[i]/2^t>=a[i-1] 可以用来抵消(前面的)乘2 从而使s[i]变小
s[i]=max(0,s[i-1]-t) s[i]最小就是0 就是不操作 前面的乘2改变的数 t都能抵消从而不改变值
a[i]<a[i-1]
例如:a[i-1]=2,a[i]=4,s[i-1]=3;
易得 t=1。a[i-1]*2*2*2=16,要使a[i]>=a[i-1]=16,那么a[i]需要乘 s[i-1]-t 个2,也就是2个2就可以满足a[i]>=16。
这时你要考虑 a[i-1]*2^t<=a[i] 此时这个a[i]一定要有相应的变化 最小变化就是乘2^t 如果前面也存在 a[j]<a[j-1]肯定也是乘2^x 这时相乘的2^y y肯定比t大了 要考虑全面 故s[i]=max(0,s[i-1]+t)
例如:a[i-1]=4,a[i]=2,s[i-1]=2;
易得 t=1。a[i-1]*2*2=16,要使a[i]>=a[i-1]=16,那么a[i]需要乘 s[i-1]+t 个2,也就是3个2就可以满足a[i]>=16。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=2e5+10;
ll a[N],s[N];
int main()
{int t;cin>>t;while(t--){int n;cin>>n;for(int i=1;i<=n;i++) cin>>a[i];memset(s,0,sizeof s);for(int i=2;i<=n;i++){ll b=a[i-1],c=a[i];ll tt=0;if(b<c){while(b*2<=c){tt++;b*=2; }s[i]=max((ll)0,s[i-1]-tt);}else {while(c<b){tt++;c*=2;}s[i]=max((ll)0,s[i-1]+tt);}}ll sum=0;for(int i=1;i<=n;i++) sum+=s[i];cout<<sum<<endl;}return 0;
}
相关文章:
)
Look Back(cf div3 905)
题意:给你一个长度为n((1≤n≤10^5)数组a[],你可以进行一个操作 使a[i]a[i]*2,问最少经过多少次这样的操作使的a[]不递减,a[i]>a[i-1]。 输入样例: 6 1 1 2 1 1 3 1 2 1 4 2 3 2 1 5 4 5 4 5 4 10 1 7 7 2 3 4 3 2 1 100 输出…...

Spring框架的发展历程
Spring框架的发展历程 自2004年以来,Spring框架已经成为Java开发人员最受欢迎的开源框架之一。它提供了一个全面的编程和配置模型,旨在简化企业级Java应用程序的开发过程。本文将详细介绍Spring框架的发展历程,以及它如何为Java开发人员提供…...

vue 级联查询5级--省/市/区/街道/社区
<template> <div> 1234 <el-select v-model="provinceVal" @change="selectProvinceFn" placeholder="请选择"> <el-option v-for="item in provinceList" :key="item.code" :label="item.name&q…...
 | 互斥量)
C++并发与多线程(8) | 互斥量
一、互斥量(mutex)的基本概念 互斥量(Mutex)是一种用于多线程编程的同步机制,用于管理共享资源的访问,以确保线程之间不会同时访问某个共享资源,从而避免竞态条件(Race Condition)和数据损坏。下面是互斥量的基本概念: 互斥性(Mutual Exclusion):互斥量用于确保一…...
Power BI 傻瓜入门 3. 选择Power BI的版本
本章内容包括: Excel与Power BI的比较选择Power BI的桌面版和服务版之间的差异了解Microsoft提供的许可选项 挑选正确版本的Power BI可能就像参观世界上最大的糖果店:你可以从许多细微差别的替代品中进行选择。选择可以归结为想要、需要、规模…...

BadNets:基于数据投毒的模型后门攻击代码(Pytorch)以MNIST为例
加载数据集 # 载入MNIST训练集和测试集 transform transforms.Compose([transforms.ToTensor(),]) train_loader datasets.MNIST(rootdata,transformtransform,trainTrue,downloadTrue) test_loader datasets.MNIST(rootdata,transformtransform,trainFalse) # 可视化样本 …...
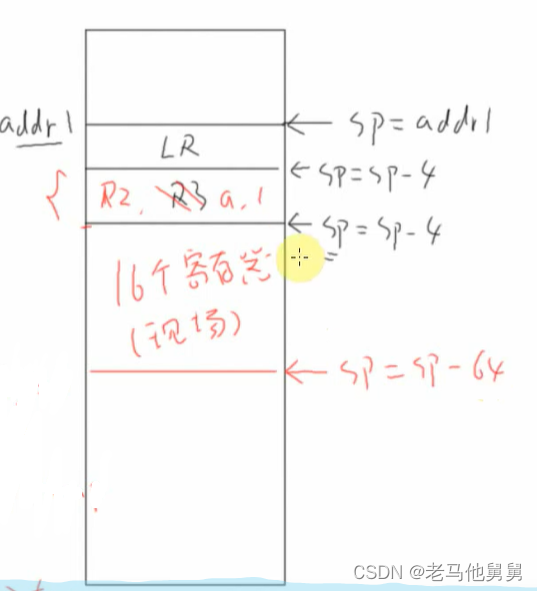
freeRTOS内部机制——栈的作用
上图中*pa 和*pb分别为R0,R1,调用C函数时,第一个参数保存在R0中第二个参数保存在R1中。这是约定。 指令保存在哪里? 指令保存在flash上面 LR等于什么? LR是返回地址,函数执行完了过后LR等于下一条指令的地址 运行…...
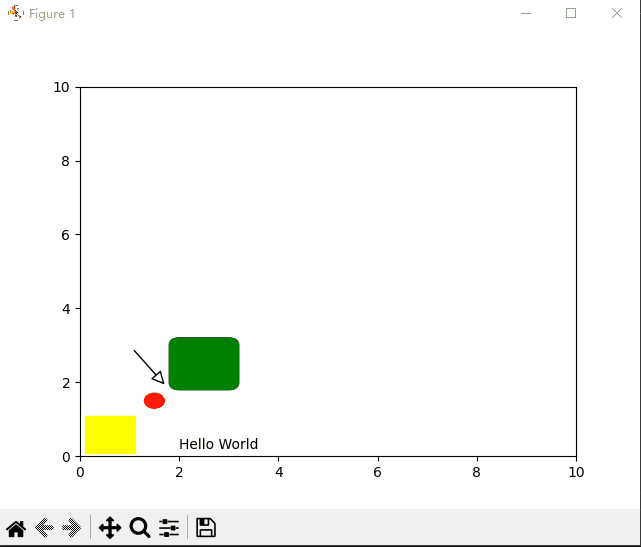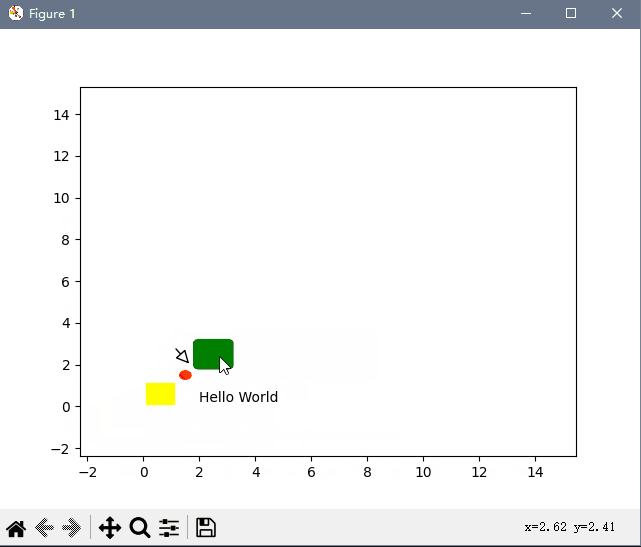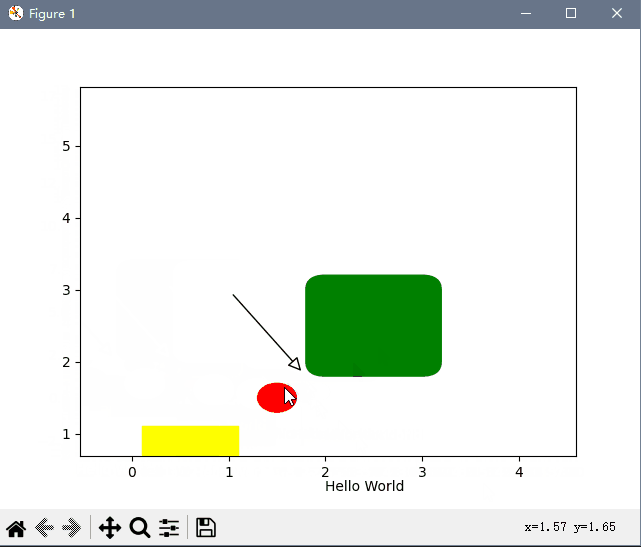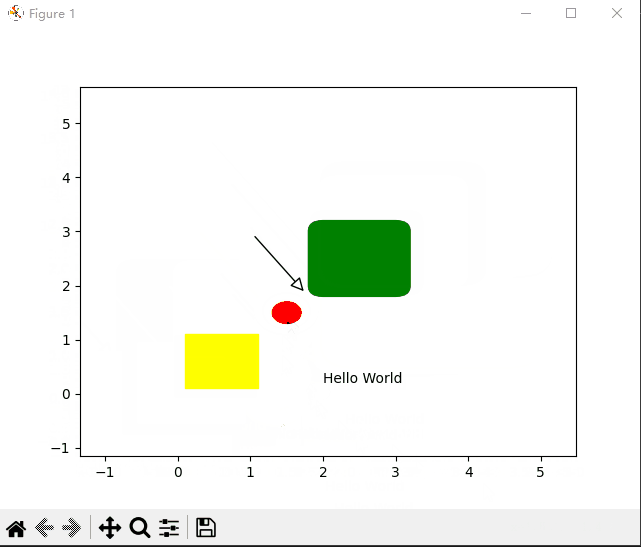
python 桌面软件开发-matplotlib画图鼠标缩放拖动
继上一篇在 Java 中缩放拖动图片后,在python matplotlib中也来实现一个自由缩放拖动的例子: python matplotlib 中缩放,较为简单,只需要通过设置要显示的 x y坐标的显示范围即可。基于此,实现一个鼠标监听回调…...

【JavaScript基础】JavaScript头等函数的理解
彻底理解JavaScript头等函数 一、函数的理解 🔥 什么是函数? 一般来说,一个函数是可以通过外部代码 调用 的一个“子程序”(或在递归的情况下由内部函数调用)。像程序本身一样,一个函数由称为函数体的一…...
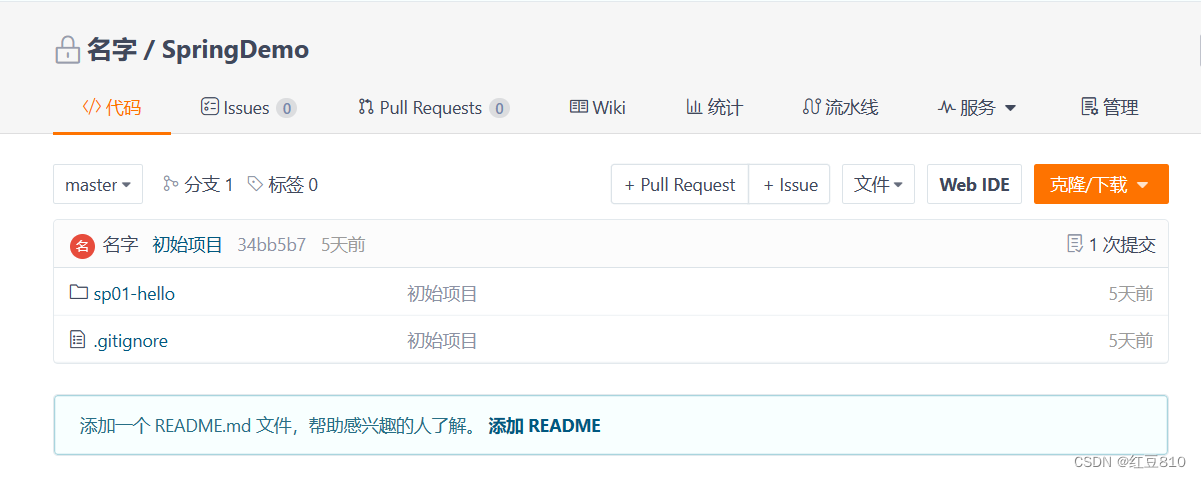
如何把项目上传到Gitee(详细教程)
找到项目根目录右键打开Git Bash Here 输入命令:git init 回车 输入命令:git status 输入命令:git add . 输入命令:git status git commit -m 项目描述 在Gitee官网注册好账号后,git 新建项目 填写补充git项目信息及…...

Ubuntu挂载windows下的共享文件夹
Ubuntu挂载windows下的共享文件夹 更新apt源 如果出现安装失败,需要更新apt源为阿里云 # 备份原始文件 sudo cp /etc/apt/sources.list.d/* /etc/apt/sources.list.d.bak/# 修改文件内容 sudo vim /etc/apt/sources.list# 替换内容为如下 deb https://mirrors.al…...
什么是WMS系统条码化管理
WMS系统是一种用于仓库管理的信息化系统,旨在提高仓库操作的效率和准确性。而在WMS系统中,条码化管理是一项关键的技术和方法,它通过将商品和物料打上条码,并利用扫描设备进行数据采集和处理,实现了仓库管理的全面自动…...

【云原生之kubernetes实战】在k8s环境下部署moredoc文库系统
【云原生之kubernetes实战】在k8s环境下部署moredoc文库系统 一、moredoc介绍1.1 moredoc简介1.2 moredoc技术栈二、本次实践介绍2.1 本次实践简介2.2 本次环境规划三、检查k8s环境3.1 检查工作节点状态3.2 检查系统pod状态四、创建mysql的secret资源4.1 创建部署目录4.2 创建密…...
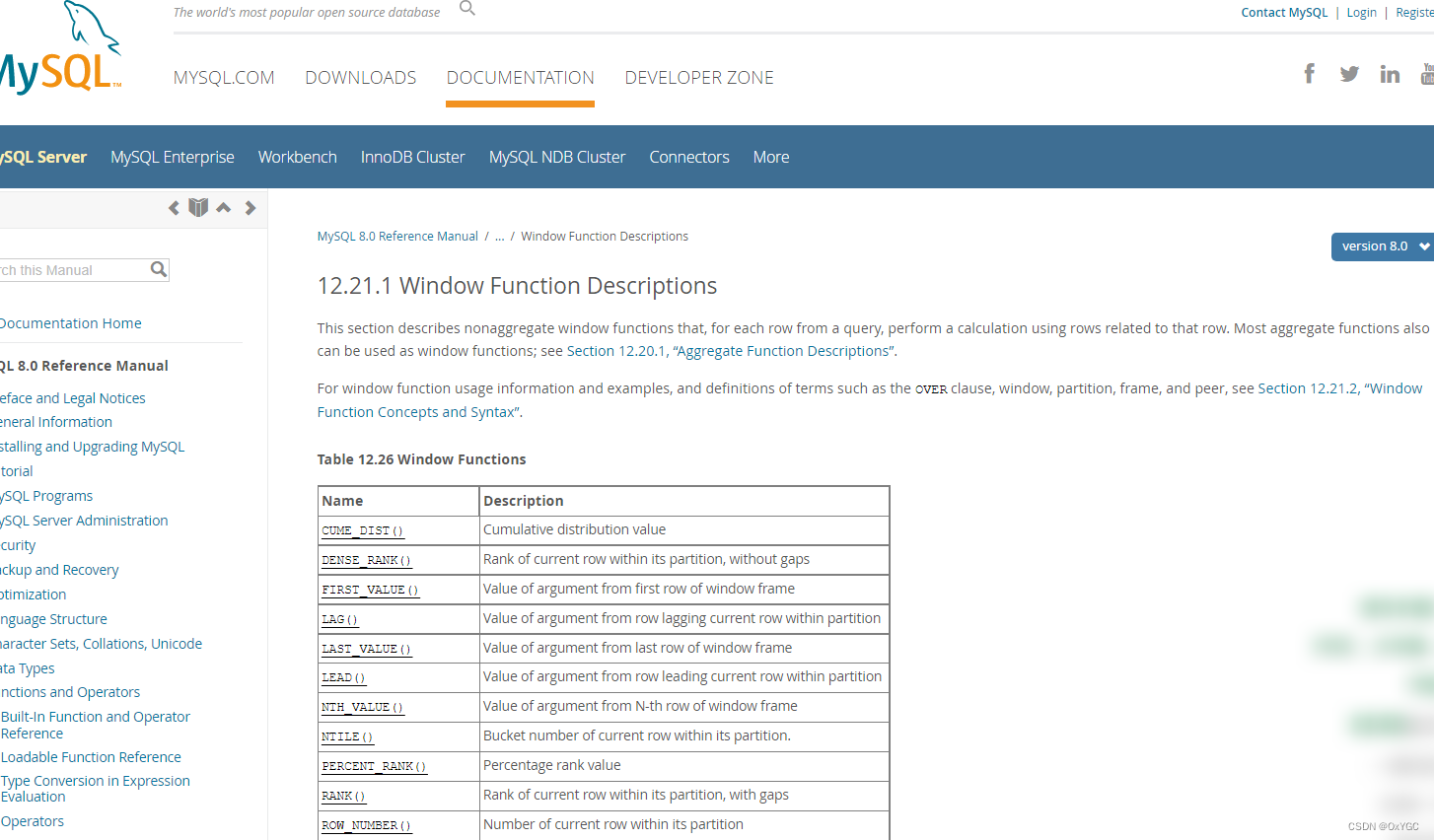
[Database] MySQL 8.x Window / Partition Function (窗口/分区函数)
🧲相关文章 [1] MySQL 系统表解析以及各项指标查询 [2] MySQL 5.7 JSON 字段的使用的处理 [3] MySQL经典练习50题 简介 MySQL 8.0版本开始支持窗口函数 官方文档 在之前的版本中已存在的大部分聚合函数,在MySQL 8 中也可以作为窗口函数来使用 方法 / …...

openGauss Meetup(天津站)精彩回顾 | openGauss天津用户组正式成立
由openGauss社区、天开发展集团、天津市软件行业协会、天大智图(天津)科技有限公司联合主办的“openGauss Meetup • 天津站”已于10月13日落下帷幕,此次活动邀请到众多业内技术专家,从技术创新、学术创新、发展创新、以及生态共建…...

linux vim 删除多行
使用linux服务器,免不了和vi编辑打交道,命令行下删除数量少还好,如果删除很多,光靠删除键一点点删除真的是头痛,还好Vi有快捷的命令可以删除多行、范围。 删除行 在Vim中删除一行的命令是dd。 以下是删除行的分步说明…...

低概率Bug,研发敷衍说复现不到
测试工作中,经常会遇到一些低概率出现的问题,如果再是个严重问题,那测试人员的压力无疑是很大的,一方面是因为低概率难以复现,另一面则是来自项目组的压力。 如何在测试时减少此类问题的重复投入,我的思考如…...
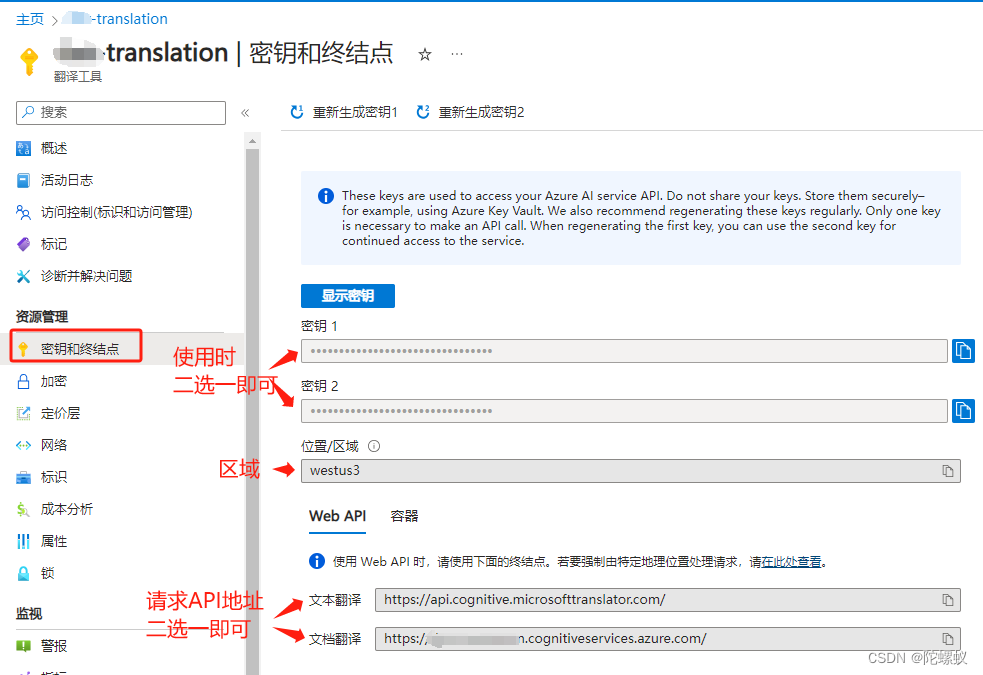
Web前端免费接入Microsoft Azure AI文本翻译,享每月2百万个字符的翻译
Azure 文本翻译是 Azure AI 翻译服务的一项基于云的 REST API 功能。 文本翻译 API 支持实时快速准确地进行源到目标文本翻译。 文本翻译软件开发工具包 (SDK) 是一组库和工具,可用于轻松地将文本翻译 REST API 功能集成到应用程序中。 文本翻译 SDK 可跨 C#/.NET、…...

1024 CSDN 程序员节-知存科技-基于存内计算芯片开发板验证语音识别
前言 在今年的 CSDN 程序员节上,我参与了这次知存科技举办的一个 AI Workshop 小活动——“基于存内计算芯片开发板验证语音识别”,并且有幸成为完成任务的学习者之一XD。上一次参与类似的活动是算能公司举办的“千校万里行”AIGC 大模型编译部署活动&a…...
)
【备考网络工程师】如何备考2023年网络工程师之错题集篇(3)
一、写在前面 其实做模拟或真题时候,总是会在关键的地方丢分,因此我也冷静下来思考一下,首先我们对做过的题涉及的知识进行一个梳理,其次就是再针对知识去做一些题目,这次只考了38分,表示很伤心࿰…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
