XTU-OJ 1187-Candy
WCB某天买了非常多的糖果并把它们分成N份,依次分别有1,2,3…,N个糖果。他想拿出其中的3份分给他的室友, 为了不让室友们闹意见,必须让这三份的糖果总数恰好能被三人均分。请问他一共有多少种不同的组合方案数?
输入
有多组输入数据,每组输入非负整数N(3≤N≤106),如果N=0,表示输入结束,这个样例不需要处理。
输出
每组数据输出一个整数独占一行,表示共有多少种方案,由于可能会很大,最后结果对109+7取模。
样例输入
3 4 5 0样例输出
1 2 4
解题思路:这题题目也说了就是一道排列组合题。 有哪些组合,可以让三份的糖果总数恰好能被三人均分?
1:三份糖果 模3余数均为1 的 糖果;
2:三份糖果 模3余数均为2 的 糖果;
3:三份糖果 模3余数均为0 的 糖果;
4:一份糖果 模3余数为1 的 糖果 + 一份糖果 模3余数均为2 的 糖果 + 一份糖果 模3余数均为0 的 糖果。
最后对这4种情况的组合数求和就行了。 (注意取模 和 爆int )
AC代码:
#include <stdio.h>const int Mod = 1e9+7;
int compute(__int64 s){ // 组合数公式 C(n,3)return (s*(s-1)*(s-2)/6) % Mod;
}int main()
{int n,N;__int64 x,y,z;__int64 ans1,ans2,ans3,ans;while (scanf("%d",&N) != EOF && N != 0){x = N/3; // x:3的倍数的 个数y = z = x;n = N%3;if (n == 1) y += 1; // y:模3余1的数 的个数else if (n == 2) y += 1, z += 1; // z:模3余2的数 的个数ans1 = compute(x);ans2 = compute(y);ans3 = compute(z);ans = (ans1+ans2+ans3+x*y*z) % Mod;printf("%I64d\n",ans);}return 0;
}相关文章:

XTU-OJ 1187-Candy
WCB某天买了非常多的糖果并把它们分成N份,依次分别有1,2,3…,N个糖果。他想拿出其中的3份分给他的室友, 为了不让室友们闹意见,必须让这三份的糖果总数恰好能被三人均分。请问他一共有多少种不同的组合方案数ÿ…...
基于 nodejs+vue城市轨道交通线路查询系统mysql
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...
电商时代,VR全景如何解决实体店难做没流量?
近日,电商和实体经济的对立成为了热门话题,尽管电商的兴起确实对线下实体店造成了一定的冲击,但实体店也不是没有办法挽救。VR全景助力线下实体店打造线上店铺,打通流量全域布局,还能实现打开产品、查看产品内部细节等…...
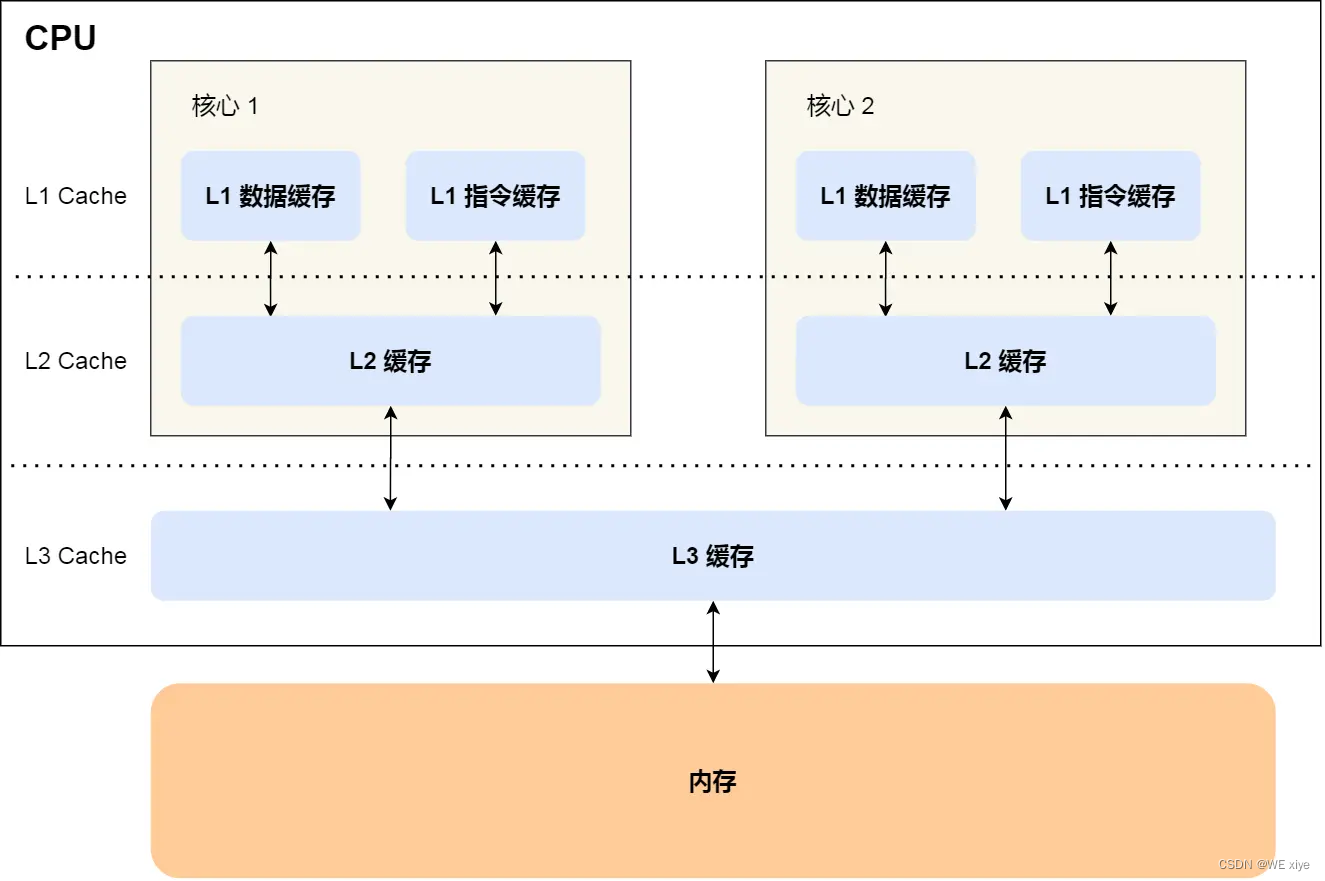
操作系统-浅谈CPU与内存
目录 计算机的基本组成CPU内存虚拟内存内存分段内存分页 CPU与内存的交互过程高速缓存cache 所有图片均来自:小林coding 计算机的基本组成 计算机由软件和硬件组成 硬件由CPU(中央处理器)存储器(内存外存)外部设备组成。 软件由应用软件和系…...
K8s 部署 CNI 网络组件+k8s 多master集群部署+负载均衡
------------------------------ 部署 CNI 网络组件 ------------------------------ ---------- 部署 flannel ---------- K8S 中 Pod 网络通信: ●Pod 内容器与容器之间的通信 在同一个 Pod 内的容器(Pod 内的容器是不会跨宿主机的)共享同一…...
若依微服务上传图片文件代理配置
在使用若依微服务文件上传时候,文件上传成功会上传到D:/ruoyi/uploadPath目录下。默认使用9300端口进行访问图片文件,现在我想把它代理到80端口应该怎么做呢? 配置前:http://localhost:9300/statics/2023/09/24/test.jpg 配置后:http://localhost/statics/2023/09/24/test…...

物联网与 Linux 的相爱相生
Linux 无疑将在物联网中扮演一个关键角色,但是其光彩将与其它的一些分享。 随着 Canonical 重新关注于赢利和新技术,我们中的一些人发现我们正在思考 Linux 未来将走向何方,IoT(物联网)是否是 Linux 的未来࿱…...
:操作浏览器)
python自动化测试(一):操作浏览器
通过Python的代码去操作浏览器的操作 目录 目录 1、导入自动化模块 2、定义打开的浏览器驱动、声明一个url变量保存打开的地址 3、使用函数:driver.get(url)打开浏览器的指定页面 4、最大化浏览器窗口:driver.maximize_window() 5、添加全局的等待…...

NReco.LambdaParser使用案例
使用案例集合: private async void RuleEngine_Click(object sender, EventArgs e){#region 获取变量string expression this.Rule.Text.Trim();string pattern "\$(.*?)\$";MatchCollection matches Regex.Matches(expression, pattern);foreach (Ma…...

苹果IOS安装IPA, plist形式 Safari 浏览器点击安装
快速链接 苹果开发者账号链接 网址: https://developer.apple.com/account 苹果应用上架链接 网址: https://appstoreconnect.apple.com/ 应用证书文件及打包 参考教程: 最新uniapp打包IOS详细步骤(2022) 证书在线制作工具 网址: https://app.121xuexi.…...
Django 注册及创建订单商品
注册功能的实现 user/views from rest_framework.generics import GenericAPIView from rest_framework.views import APIViewfrom apps.user.models import User from apps.user.serializers import UserSerializer from utils import ResponseMessage from utils.jwt_auth …...

15、Python -- 阶段总结:变量与流程控制
目录 变量变量没有类型,数据有类型 表达式程序流程 变量 变量:编程的本质就是处理数据,数据需要用变量保存 Python语言的特征: 所有变量无需声明,即可使用 变量没有类型 变量没有类型,数据有类型 已学过…...
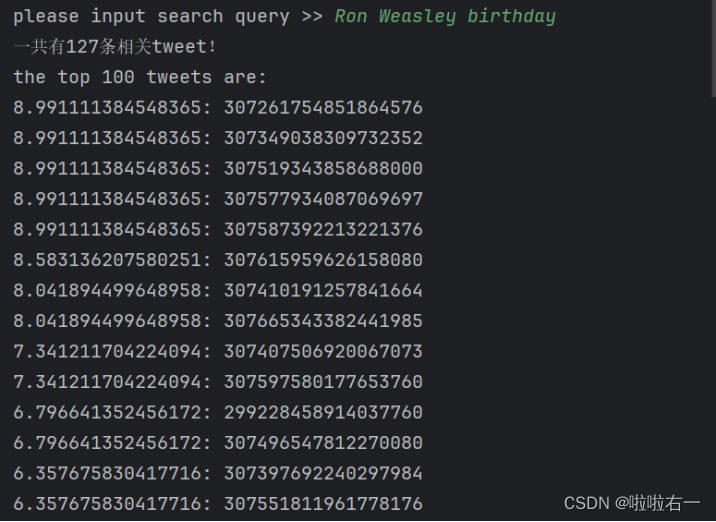
信息检索与数据挖掘 | 【实验】排名检索模型
文章目录 📚实验内容📚相关概念📚实验步骤🐇分词预处理🐇构建倒排索引表🐇计算query和各个文档的相似度🐇queries预处理及检索函数🔥对输入的文本进行词法分析和标准化处理…...

玩转AIGC:打造令人印象深刻的AI对话Prompt
玩转AIGC:打造令人印象深刻的AI对话Prompt 《玩转AIGC:打造令人印象深刻的AI对话Prompt》摘要引言正文良好的Prompt:引发AI深度交流的法宝 ✨探讨不同的提问方式1. 常规提问2. 创意提问 对话交流的艺术:倾听与引导的巧妙平衡 ⚖️…...

uniapp vue国际化 i18n
一、安装 vue-i18n npm i vue-i18n 二、新建i18n目录 1、en.json 内容 {"loginPage":{"namePh":"Please enter your login account","passwordPh":"Please enter password"} } 2、zh-CN.json 内容 {"loginPage&qu…...

Docker 启动远程服务访问不了
今天一下午在弄这个 1、防火墙是否关了 firewall-cmd --state2、ip转发开没开 sysctl net.ipv4.ip_forward3、service iptables是不是打开并拦截了 4、检查docker启动的端口号是否一致,或者启动时对不对 5、检查docker的服务是否起来了,比如你的端口号…...
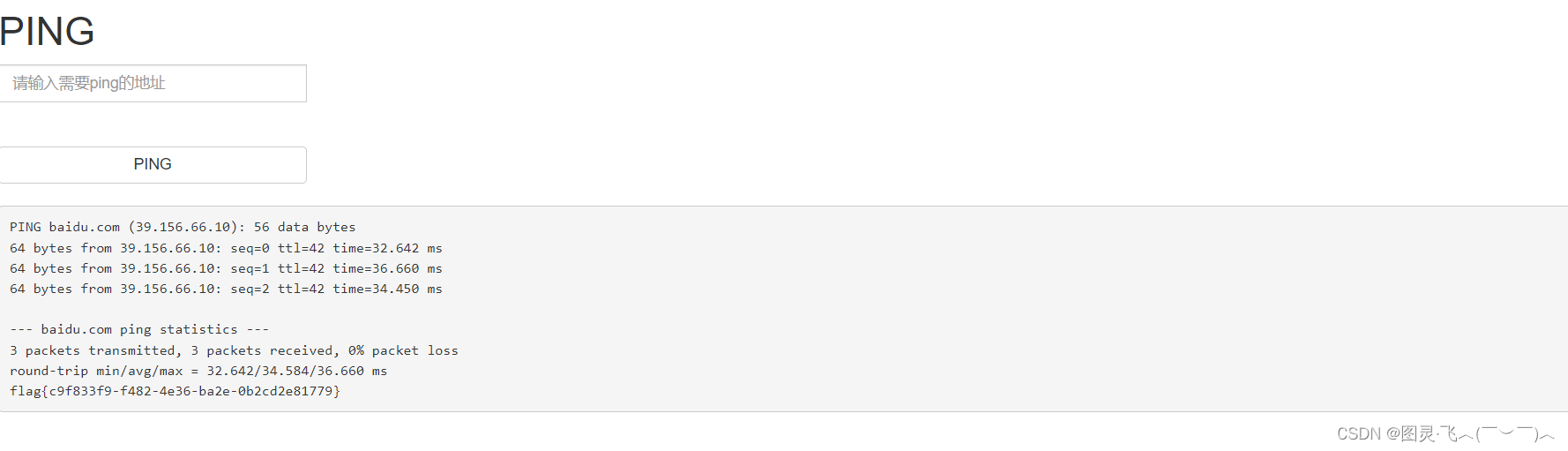
[ACTF2020 新生赛]Exec
【解题过程】 1.打开链接 得到一个能ping 的网站,可以推测这个可以在终端运行的网站。 2.解题思路 在执行的时候我们可以想到命令执行的“;”分号的作用:命令用分号分隔开来,表示它们是两个独立的命令,需要依次执行。…...

Git(三).git 文件夹详解
目录 一、初始化新仓库二、.git 目录2.1 hooks 文件夹2.2 info 文件夹2.3 logs 文件夹2.4 objects 文件夹【重要】2.5 refs 文件夹【重要】2.6 COMMIT_EDITMSG2.7 config2.8 description2.9 FETCH_HEAD2.10 HEAD【重要】2.11 index【重要】2.12 ORIG_HEAD2.13 packed-refs 官网…...

esp32-S3 + visual studio code 开发环境搭建
一、首先在下面链接网页中下载esp-idf v5.1.1离线安装包 ,并安装到指定位置。dl.espressif.cn/dl/esp-idf/https://dl.espressif.cn/dl/esp-idf/ 安装过程中会提示需要长路径支持,所以windows系统需要开启长路径使能 Step 1: 打开运行&…...

4.1 网络基础之网络IO
一、编写基本服务程序流程 1、创建套接字 #include <sys/types.h> #include <sys/socket.h>int socket(int domain, int type, int protocol);/* * 参数domain通讯协议族: * PF_INET IPv4互联网协议族(常用) * PF_INET6 …...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
