vue项目切换页面白屏的解决方案
问题描述
1、页面切换后白屏,同时切换回上一个页面同样白屏
2、刷新后正常显示
3、有警告:Component inside <Transition> renders non-element root node that cannot be animated
解决方法
<Transition>中的组件呈现不能动画化的非元素根节点
也就是说,组件内必须有一个根元素
之前:
<template><div>你好</div><div>您好</div>
</template>现在:
<template><div><div>你好</div><div>您好</div></div>
</template>原来的vue2中,template下是必须有一个根元素的,vue3变为可多个根元素
相关文章:

vue项目切换页面白屏的解决方案
问题描述 1、页面切换后白屏,同时切换回上一个页面同样白屏 2、刷新后正常显示 3、有警告:Component inside <Transition> renders non-element root node that cannot be animated 解决方法 <Transition>中的组件呈现不能动画化的非元素根…...

5G vs 4G
5G与4G的关键性能指标对比 指标名称流量密度连接密度空口时延移动性能效指标用户体验速率频谱效率峰值速率4G 参考值0.1 M b i t / s / m 2 Mbit/s/m^2 Mbit/s/m2 1 ∗ 1 0 5 / k m 2 1*10^5/km^2 1∗105/km210ms350km/h1倍10Mbit/s1倍1Gbit/s5G 参考值10 M b i t / s / m 2 M…...
【JavaEE重点知识归纳】第11节:认识异常
目录 一:异常的概念和体系结构 1.概念 2.体系结构 3.异常分类 二:异常的处理 1.防御式编程 2.异常的抛出 3.异常的捕获 4.异常的处理流程 三:自定义异常 一:异常的概念和体系结构 1.概念 (1)在…...

一键自助建站系统api版系统源码
自助建站系统,一建建站系统api版,自动建站 安装推荐php7.2或7.2以下都行 可使用虚拟主机或者服务器进行搭建。 分站进入网站后台 域名/admin 初始账号123456qq.com密码123456 找到后台的网站设置 将主站域名及你在主站的通信secretId和通信secretKey填进去。 即可正常使用 通信…...

全国三维数字化创新设计大赛湖北赛区省赛成功举办
须弥芥子,数字如海。10月14日—15日,2023 年数字科技文化节——第16届全国三维数字化创新设计大赛湖北赛区省赛暨产教联合体大会在武汉软件工程职业学院成功举行。 (大赛全体专家领导合影) 全国三维数字化创新设计大赛组委会副秘…...

OpenCV #以图搜图:均值哈希算法(Average Hash Algorithm)原理与实验
1. 介绍 均值哈希算法(Average Hash Algorithm) 是哈希算法的一种,主要用来做相似图片的搜索工作。 2. 原理 均值哈希算法(aHash)首先将原图像缩小成一个固定大小的像素图像,然后将图像转换为灰度图像&am…...

博通BCM575系列RDMA网卡驱动bnxt_re分析(一)
简介 整个BCM系列驱动分成以太网部分(bnxt_en.ko)和RDMA部分(bnxt_re.ko), 两个模块之间通过内核的auxiliary_bus进行管理.我们主要分析下bnxt_re驱动. 代码结构 这个驱动的核心是 qplib_fp.c, 这个文件主要包含了驱动的数据路径, 包括Post Send, Post Recv, Poll CQ流程的实…...

集合总结-
Collection 常用方法 package com.test01;import java.util.ArrayList; import java.util.Collection; /*添加元素---boolean add(E e);移除元素---boolean remove(Object c);判断元素是否存在---boolean contains(Object c);*/ public class S {public static void main(Str…...
【考研向】【按概率论学习章节总结】)
【知识串联】概率论中的值和量(随机变量/数字特征/参数估计)【考研向】【按概率论学习章节总结】
就我的概率论学习经验来看,这两个概念极易混淆,并且极为重点,然而,在概率论的前几章学习中,如果只是计算,对这方面的辨析不清并没有问题。然而,到了后面的参数估计部分,却可能出现问…...

上游服务不可用了,下游服务如何应对?
上游服务不可用了,下游服务如何应对? 引言 在系统中,上游服务和下游服务是两个关键概念。上游服务通常指的是提供某种功能或数据的服务端,它接收来自下游服务的请求,并根据请求进行处理和响应。下游服务通常指的是发…...

WebGL笔记:矩阵的变换之平移的实现
矩阵的变换 变换 变换有三种状态:平移、旋转、缩放。当我们变换一个图形时,实际上就是在移动这个图形的所有顶点。解释 webgl 要绘图的话,它是先定顶点的,就比如说我要画个三角形,那它会先把这三角形的三个顶点定出来…...

XTU-OJ 1187-Candy
WCB某天买了非常多的糖果并把它们分成N份,依次分别有1,2,3…,N个糖果。他想拿出其中的3份分给他的室友, 为了不让室友们闹意见,必须让这三份的糖果总数恰好能被三人均分。请问他一共有多少种不同的组合方案数ÿ…...
基于 nodejs+vue城市轨道交通线路查询系统mysql
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...
电商时代,VR全景如何解决实体店难做没流量?
近日,电商和实体经济的对立成为了热门话题,尽管电商的兴起确实对线下实体店造成了一定的冲击,但实体店也不是没有办法挽救。VR全景助力线下实体店打造线上店铺,打通流量全域布局,还能实现打开产品、查看产品内部细节等…...
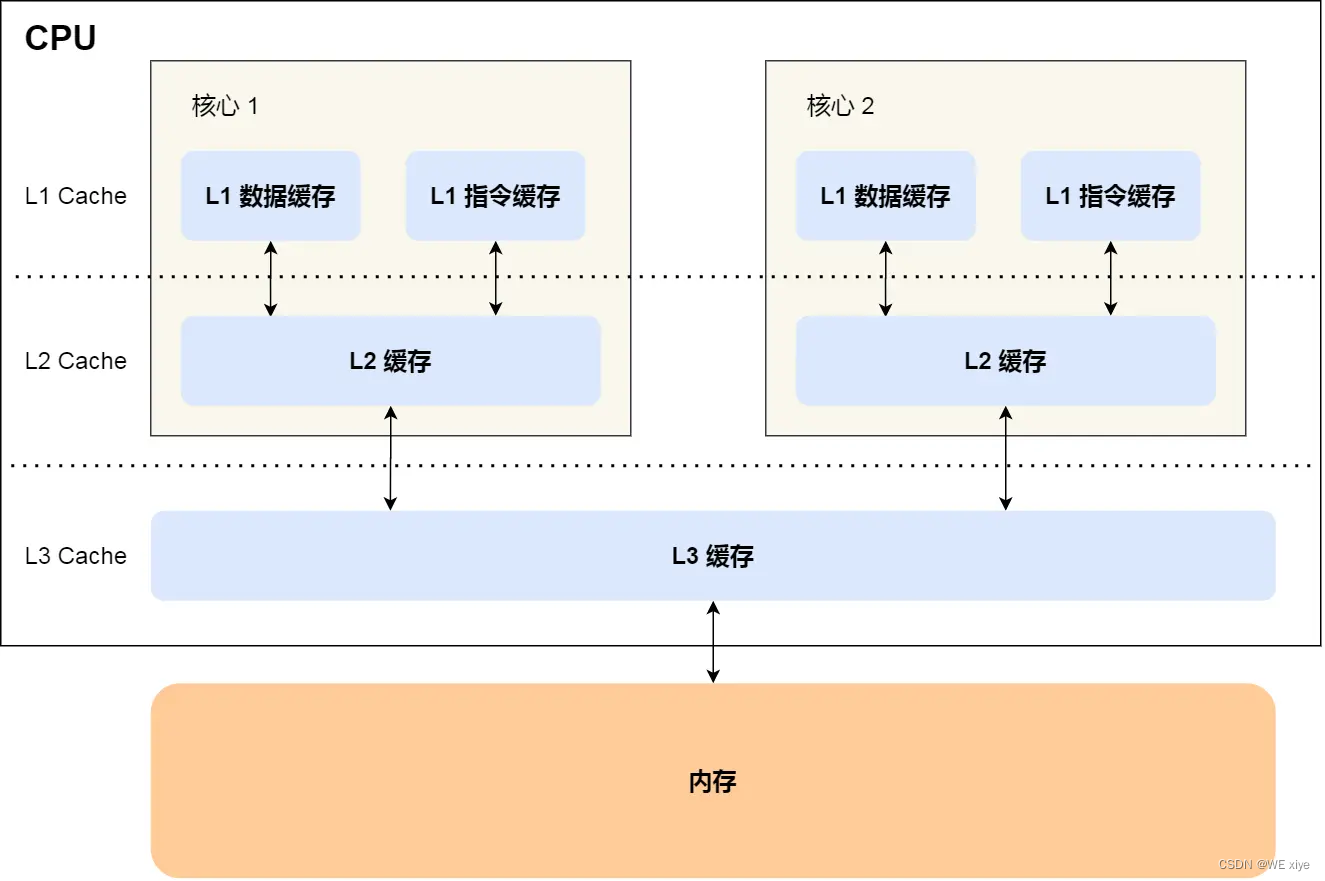
操作系统-浅谈CPU与内存
目录 计算机的基本组成CPU内存虚拟内存内存分段内存分页 CPU与内存的交互过程高速缓存cache 所有图片均来自:小林coding 计算机的基本组成 计算机由软件和硬件组成 硬件由CPU(中央处理器)存储器(内存外存)外部设备组成。 软件由应用软件和系…...
K8s 部署 CNI 网络组件+k8s 多master集群部署+负载均衡
------------------------------ 部署 CNI 网络组件 ------------------------------ ---------- 部署 flannel ---------- K8S 中 Pod 网络通信: ●Pod 内容器与容器之间的通信 在同一个 Pod 内的容器(Pod 内的容器是不会跨宿主机的)共享同一…...
若依微服务上传图片文件代理配置
在使用若依微服务文件上传时候,文件上传成功会上传到D:/ruoyi/uploadPath目录下。默认使用9300端口进行访问图片文件,现在我想把它代理到80端口应该怎么做呢? 配置前:http://localhost:9300/statics/2023/09/24/test.jpg 配置后:http://localhost/statics/2023/09/24/test…...

物联网与 Linux 的相爱相生
Linux 无疑将在物联网中扮演一个关键角色,但是其光彩将与其它的一些分享。 随着 Canonical 重新关注于赢利和新技术,我们中的一些人发现我们正在思考 Linux 未来将走向何方,IoT(物联网)是否是 Linux 的未来࿱…...
:操作浏览器)
python自动化测试(一):操作浏览器
通过Python的代码去操作浏览器的操作 目录 目录 1、导入自动化模块 2、定义打开的浏览器驱动、声明一个url变量保存打开的地址 3、使用函数:driver.get(url)打开浏览器的指定页面 4、最大化浏览器窗口:driver.maximize_window() 5、添加全局的等待…...

NReco.LambdaParser使用案例
使用案例集合: private async void RuleEngine_Click(object sender, EventArgs e){#region 获取变量string expression this.Rule.Text.Trim();string pattern "\$(.*?)\$";MatchCollection matches Regex.Matches(expression, pattern);foreach (Ma…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
