WebGL笔记:矩阵的变换之平移的实现
矩阵的变换
变换
- 变换有三种状态:平移、旋转、缩放。
- 当我们变换一个图形时,实际上就是在移动这个图形的所有顶点。
- 解释
- webgl 要绘图的话,它是先定顶点的,就比如说我要画个三角形,那它会先把这三角形的三个顶点定出来。
- 然后它再考虑以什么样的方式去绘制这个三角形, 就比如说在 gl.drawArrays(gl.TRIANGLES, 0, 3) 这个方法
- 第一个参数是 TRIANGLES,让它画一个独立三角形,我依次连接这三个点,然后逐片元给它们填充颜色
- 接下来我就可以对三角形进行变换操作了,比如:旋转,缩放,平移。
- 我在做这三种操作的时候,实际上就是改变了三角形的顶点位置
平移
-
对图形的平移啊,就是对图形所有顶点的平移
-
举个简单的例子
- 就比如说已知点p的位置是(x,y,z)
- 那我要对它进行一个相对的移动,
- 移动的三个分量分别是 tx, ty, tz, 那么求它移动完之后的位置 p’ (x’, y’, z’)
- 只要让它这三个分量做加法就可以了
-
即,如下图
x'=x+tx y'=y+ty z'=z+tz
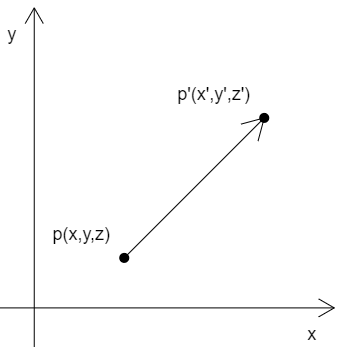
- 如果上面这个图形中并非只有一个顶点,而是三个顶点或者更多,那么所有的顶点也是按同样的原理去进行位移的
- 就比如下面这个图这个三角形在位移的时候啊,其实上也就是它的所有顶点去做一个相对的位移

向量的加法
- 在实际的编码中,要有一个向量的概念。
- 就比如说 (x,y,z) 这三个量可以构成一个三维点位
- 我们可以说它是一个顶点位置,也可以说它是一个向量, 至于这个 (x,y,z) 到底是什么?我们要看它是要做什么的
- 就比如说我把点p(x,y,z)作为点位的时候,那它就是个点
- 如果我把p的移动距离 tx, ty, tz 封装成一个对象 pt(tx,ty,tz), 那么 pt 就是一个向量,一个为点p 指明移动方向和距离的向量
- 那么,点 p 的移动结果 p’ 就可以这么写:p’ = p + pt
- 由此可知,顶点的位移,就是向量的加法
编写向量加法代码
-
在GLSLES语言里,是直接可以进行向量运算的,下面是顶点着色器里的代码:
attribute vec4 a_Position; vec4 translation = vec4(0, 0.2, 0, 0); void main() {gl_Position = a_Position + translation; }- a_Position 是原始点位,属于attribute 变量
- translation 是顶点着色器里的私有变量,没有向外部暴露,属于4维向量
- a_Position + translation 便是着色器内的向量加法,这里是对原始点位进行位移
-
基于对初始的这个a_Position 点位进行一个位移的话,那我可以直接让它加上一个四维的向量,就比如这里的这个translation,就是我声明的一个个四四维向量,让它直接加上即可
-
上述 translation 是写死的 ,我们也可以把 translation 变量暴露出去,让js可以修改图形位置:
<script id="vertexShader" type="x-shader/x-vertex">attribute vec4 a_Position;uniform vec4 u_Translation;void main() {gl_Position = a_Position + u_Translation;} </script> -
在js 中修改uniform 变量的方法,我们之前已经说过:
// 获取 uniform 变量 const u_Translation = gl.getUniformLocation(gl.program, 'u_Translation'); // 为 uniform 变量赋值 gl.uniform4f(u_Translation, 0, 0.5, 0, 0); -
之后,可以加一段逐帧动画:
let y = 0; !(function animate() {y += 0.02;if(y > 1) y = -1;gl.uniform4f(u_Translation, 0, y, 0, 0);gl.clear(gl.COLOR_BUFFER_BIT);gl.drawArrays(gl.TRIANGLES, 0, 3);requestAnimationFrame(animate) })()

完整代码
<canvas id="canvas"></canvas>
<script id="vertexShader" type="x-shader/x-vertex">attribute vec4 a_Position;uniform vec4 u_Translation;void main() {gl_Position = a_Position + u_Translation;}
</script>
<script id="fragmentShader" type="x-shader/x-fragment">void main() {gl_FragColor = vec4(1.0,1.0,0.0,1.0);}
</script>
<script type="module">// 这里参考之前博文代码import { initShaders } from './util.js';const canvas = document.getElementById('canvas');canvas.width = window.innerWidth;canvas.height = window.innerHeight;const gl = canvas.getContext('webgl');const vsSource = document.getElementById('vertexShader').innerText;const fsSource = document.getElementById('fragmentShader').innerText;initShaders(gl, vsSource, fsSource);const vertices = new Float32Array([0.0, 0.1,-0.1, -0.1,0.1, -0.1])const vertexBuffer = gl.createBuffer();gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);const a_Position = gl.getAttribLocation(gl.program, 'a_Position');gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);gl.enableVertexAttribArray(a_Position);//获取uniform 变量const u_Translation = gl.getUniformLocation(gl.program, 'u_Translation');//为uniform 变量赋值gl.uniform4f(u_Translation, 0, 0.5, 0, 0);gl.clearColor(0.0, 0.0, 0.0, 1.0);gl.clear(gl.COLOR_BUFFER_BIT);gl.drawArrays(gl.TRIANGLES, 0, 3);let y = 0!(function animate() {y += 0.02;if (y > 1) y = -1;gl.uniform4f(u_Translation, 0, y, 0, 0);gl.clear(gl.COLOR_BUFFER_BIT);gl.drawArrays(gl.TRIANGLES, 0, 3);requestAnimationFrame(animate);})()
</script>
相关文章:

WebGL笔记:矩阵的变换之平移的实现
矩阵的变换 变换 变换有三种状态:平移、旋转、缩放。当我们变换一个图形时,实际上就是在移动这个图形的所有顶点。解释 webgl 要绘图的话,它是先定顶点的,就比如说我要画个三角形,那它会先把这三角形的三个顶点定出来…...

XTU-OJ 1187-Candy
WCB某天买了非常多的糖果并把它们分成N份,依次分别有1,2,3…,N个糖果。他想拿出其中的3份分给他的室友, 为了不让室友们闹意见,必须让这三份的糖果总数恰好能被三人均分。请问他一共有多少种不同的组合方案数ÿ…...
基于 nodejs+vue城市轨道交通线路查询系统mysql
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...
电商时代,VR全景如何解决实体店难做没流量?
近日,电商和实体经济的对立成为了热门话题,尽管电商的兴起确实对线下实体店造成了一定的冲击,但实体店也不是没有办法挽救。VR全景助力线下实体店打造线上店铺,打通流量全域布局,还能实现打开产品、查看产品内部细节等…...
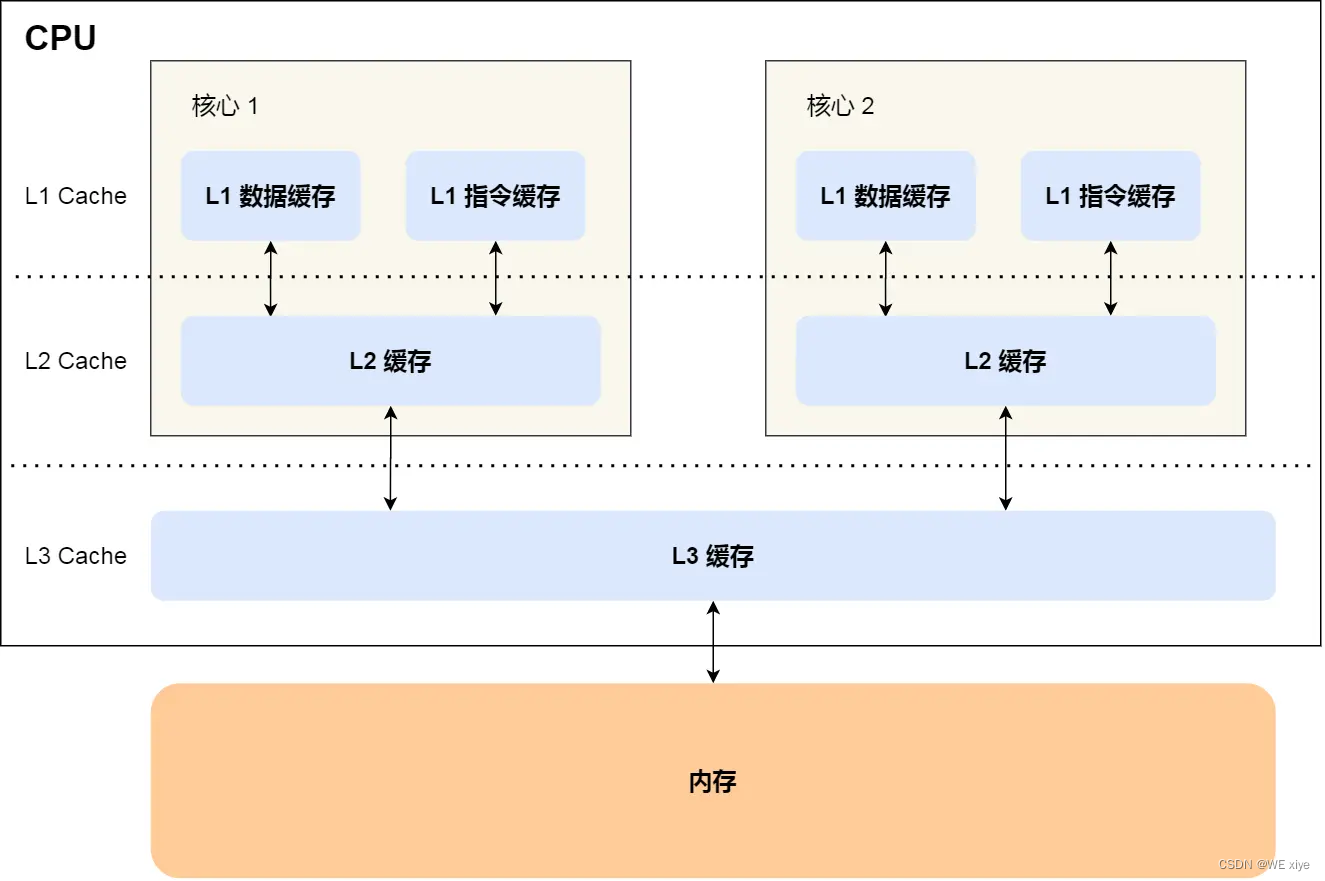
操作系统-浅谈CPU与内存
目录 计算机的基本组成CPU内存虚拟内存内存分段内存分页 CPU与内存的交互过程高速缓存cache 所有图片均来自:小林coding 计算机的基本组成 计算机由软件和硬件组成 硬件由CPU(中央处理器)存储器(内存外存)外部设备组成。 软件由应用软件和系…...
K8s 部署 CNI 网络组件+k8s 多master集群部署+负载均衡
------------------------------ 部署 CNI 网络组件 ------------------------------ ---------- 部署 flannel ---------- K8S 中 Pod 网络通信: ●Pod 内容器与容器之间的通信 在同一个 Pod 内的容器(Pod 内的容器是不会跨宿主机的)共享同一…...
若依微服务上传图片文件代理配置
在使用若依微服务文件上传时候,文件上传成功会上传到D:/ruoyi/uploadPath目录下。默认使用9300端口进行访问图片文件,现在我想把它代理到80端口应该怎么做呢? 配置前:http://localhost:9300/statics/2023/09/24/test.jpg 配置后:http://localhost/statics/2023/09/24/test…...

物联网与 Linux 的相爱相生
Linux 无疑将在物联网中扮演一个关键角色,但是其光彩将与其它的一些分享。 随着 Canonical 重新关注于赢利和新技术,我们中的一些人发现我们正在思考 Linux 未来将走向何方,IoT(物联网)是否是 Linux 的未来࿱…...
:操作浏览器)
python自动化测试(一):操作浏览器
通过Python的代码去操作浏览器的操作 目录 目录 1、导入自动化模块 2、定义打开的浏览器驱动、声明一个url变量保存打开的地址 3、使用函数:driver.get(url)打开浏览器的指定页面 4、最大化浏览器窗口:driver.maximize_window() 5、添加全局的等待…...

NReco.LambdaParser使用案例
使用案例集合: private async void RuleEngine_Click(object sender, EventArgs e){#region 获取变量string expression this.Rule.Text.Trim();string pattern "\$(.*?)\$";MatchCollection matches Regex.Matches(expression, pattern);foreach (Ma…...

苹果IOS安装IPA, plist形式 Safari 浏览器点击安装
快速链接 苹果开发者账号链接 网址: https://developer.apple.com/account 苹果应用上架链接 网址: https://appstoreconnect.apple.com/ 应用证书文件及打包 参考教程: 最新uniapp打包IOS详细步骤(2022) 证书在线制作工具 网址: https://app.121xuexi.…...
Django 注册及创建订单商品
注册功能的实现 user/views from rest_framework.generics import GenericAPIView from rest_framework.views import APIViewfrom apps.user.models import User from apps.user.serializers import UserSerializer from utils import ResponseMessage from utils.jwt_auth …...

15、Python -- 阶段总结:变量与流程控制
目录 变量变量没有类型,数据有类型 表达式程序流程 变量 变量:编程的本质就是处理数据,数据需要用变量保存 Python语言的特征: 所有变量无需声明,即可使用 变量没有类型 变量没有类型,数据有类型 已学过…...
信息检索与数据挖掘 | 【实验】排名检索模型
文章目录 📚实验内容📚相关概念📚实验步骤🐇分词预处理🐇构建倒排索引表🐇计算query和各个文档的相似度🐇queries预处理及检索函数🔥对输入的文本进行词法分析和标准化处理…...

玩转AIGC:打造令人印象深刻的AI对话Prompt
玩转AIGC:打造令人印象深刻的AI对话Prompt 《玩转AIGC:打造令人印象深刻的AI对话Prompt》摘要引言正文良好的Prompt:引发AI深度交流的法宝 ✨探讨不同的提问方式1. 常规提问2. 创意提问 对话交流的艺术:倾听与引导的巧妙平衡 ⚖️…...

uniapp vue国际化 i18n
一、安装 vue-i18n npm i vue-i18n 二、新建i18n目录 1、en.json 内容 {"loginPage":{"namePh":"Please enter your login account","passwordPh":"Please enter password"} } 2、zh-CN.json 内容 {"loginPage&qu…...

Docker 启动远程服务访问不了
今天一下午在弄这个 1、防火墙是否关了 firewall-cmd --state2、ip转发开没开 sysctl net.ipv4.ip_forward3、service iptables是不是打开并拦截了 4、检查docker启动的端口号是否一致,或者启动时对不对 5、检查docker的服务是否起来了,比如你的端口号…...
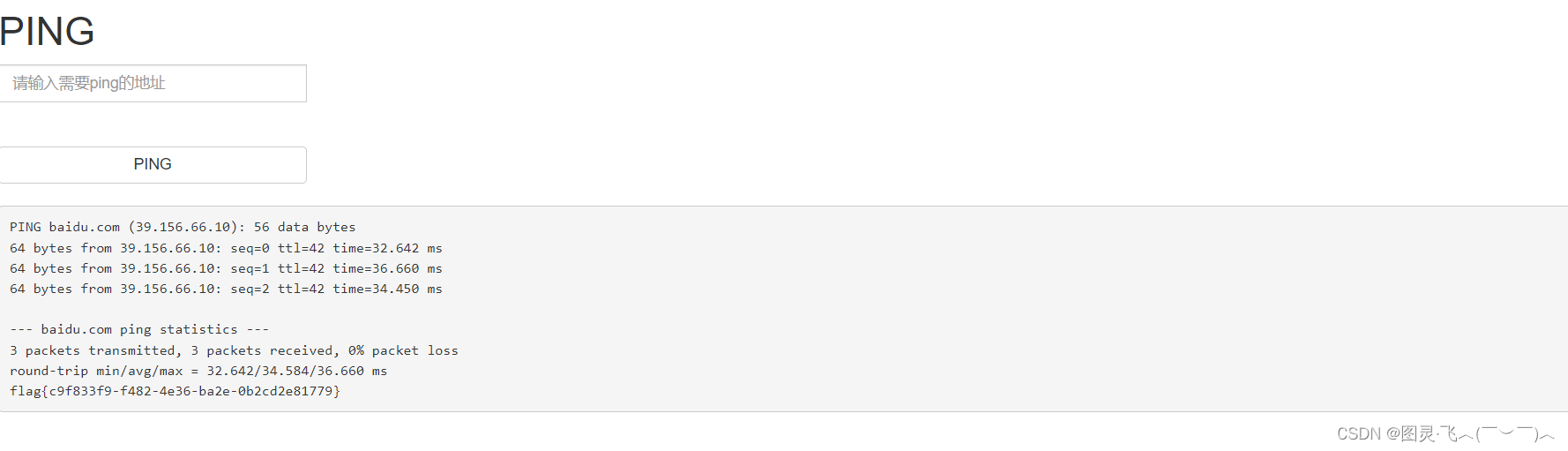
[ACTF2020 新生赛]Exec
【解题过程】 1.打开链接 得到一个能ping 的网站,可以推测这个可以在终端运行的网站。 2.解题思路 在执行的时候我们可以想到命令执行的“;”分号的作用:命令用分号分隔开来,表示它们是两个独立的命令,需要依次执行。…...

Git(三).git 文件夹详解
目录 一、初始化新仓库二、.git 目录2.1 hooks 文件夹2.2 info 文件夹2.3 logs 文件夹2.4 objects 文件夹【重要】2.5 refs 文件夹【重要】2.6 COMMIT_EDITMSG2.7 config2.8 description2.9 FETCH_HEAD2.10 HEAD【重要】2.11 index【重要】2.12 ORIG_HEAD2.13 packed-refs 官网…...

esp32-S3 + visual studio code 开发环境搭建
一、首先在下面链接网页中下载esp-idf v5.1.1离线安装包 ,并安装到指定位置。dl.espressif.cn/dl/esp-idf/https://dl.espressif.cn/dl/esp-idf/ 安装过程中会提示需要长路径支持,所以windows系统需要开启长路径使能 Step 1: 打开运行&…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...
