【知识串联】概率论中的值和量(随机变量/数字特征/参数估计)【考研向】【按概率论学习章节总结】
就我的概率论学习经验来看,这两个概念极易混淆,并且极为重点,然而,在概率论的前几章学习中,如果只是计算,对这方面的辨析不清并没有问题。然而,到了后面的参数估计部分,却可能出现问题,而这些问题是比较隐晦而且难以发现的,并且鲜有老师强调。因此,就这方面希望能够帮助同样对概率论的这部分内容有疑惑的同学。
随机变量
首先,在学习概率最开始的时候,我们接触了随机变量X,它是一种量,就是说它是变化的(这是我的理解方式)。对于这个随机变量X,我们怎么样才能让它定下来呢?通过抽样的方式。
举个例子,随机变量X(我其实感觉这个地方和最开始的事件容易混淆,我姑且把事件和随机变量混为一谈了(这个部分博友有更好的说法恳请指正))我可以说是抛硬币了,那么我只有抛了,才能知道这个值是多少,否则单论这个量(抛硬币),我是不能得出任何有用的信息的,我们只有通过抛硬币,才能发现X,X是抽象的,是被我们观察了无数次的实验结果所定义的(我姑且这么阐释了)。
当硬币抛出后,我们有了第一个样本x1,这个不一样了,我们叫它样本值x1,它是一个值。是有确切的大小的。至此,我们的前三章的值和量解决完毕。
数字特征
在第四章,我们接触到了新的东西,叫做数字特征,比如期望EX,方差DX,它们是确切的值,我想也是显而易见的。
对于一个随机变量X,假设它是服从标准正态分布的,显然它的期望是0,方差是1,是确定的值。
至此,我们的第四章的值和量解决完毕。
参数估计
在后面的几章中,我们接触了比较多的值和量,极大似然估计量,无偏估计量,样本均值,等等。在这里我们抽取两组进行说明,(样本均值,样本方差)和(期望,方差),极大似然估计值和极大似然估计量。
样本均值和样本方差,他们是量(这个地方是很容易混淆的)。
期望和方差,他们是值。
可以这么理解,样本均值是X拔,是n分之1乘以X的求和,既然X是量,那么X拔当然也是量(见补充),同理可得样本方差。
对于极大似然估计值和极大似然估计量,有了前面的铺垫,我们可以比较清晰的解决了。
极大似然估计值是θ,是值。
极大似然估计量是θ尖,是量。
在求解极大似然估计的时候,我们发现,最开始求解极大似然估计值的时候,我们都是用的x。因为值要和值对应,(极大似然估计值和样本值相对应)。
在求解极大似然估计量的时候,我们发现,在最后一步往往是,我们转换成了θ尖,这个时候,对应的x变成了X,这是因为,量要和量对应(随机变量和极大似然估计量对应)。
这个应该怎么理解呢?这里给出一个我个人的看法。
虽然样本均值和样本方差都是值,但是就像在随机变量中,我们可以通过抽样x来观察X的性质一样,在样本均值和样本方差的观察中,我们也是通过抽样样本来估计样本均值和方差。
于是,在极大似然估计的时候,我们往往可以看到,前一步θ对应x,后一步就跳到θ尖对应X了,或者可以说,我们无法得到量,即便是样本的量我们也无法得到,但是我们可以用样本值去估计样本的量,因此,通过同步替换,可以达到用样本值代替(估计)量的效果。有了这个样本的估计量,我们再用样本的估计量去估计随机变量的数字特征(值)
样本的观测值 --------> 样本的估计量 --------> 随机变量的数字特征
第一步中,我们用样本的观测值代替样本的估计量,是因为我们假设我们经过足够多的观测后,我们可以得到随机变量的性质(基于大数定律),然而在现实生活中,我们不可能进行无穷无尽的观测,因此,就用有限次观测值来近似量。
在第二步中,我们用样本的估计量来计算随机变量的数字特征就是我们在第一步的假设的延拓(比如套个D或者E,本质上就是等价变形?基于第一步的假设?)(这部分差不多可能是车轱辘话了?我暂且做个不清晰的叙述了,欢迎博友进行补充)
再举一个例子,通过样本方差S方去估计随机变量的方差,我们也是通过在S方上套一个D,就可以将其变为值,就可以进行估计了(上述的第二步)
至此,我们概率论所有重要的值和量解析完毕。
补充
X是随机变量g(X)当然也是随机变量,x是样本值,g(x)当然也是值(似乎没这么考过。。)。
相关文章:
【考研向】【按概率论学习章节总结】)
【知识串联】概率论中的值和量(随机变量/数字特征/参数估计)【考研向】【按概率论学习章节总结】
就我的概率论学习经验来看,这两个概念极易混淆,并且极为重点,然而,在概率论的前几章学习中,如果只是计算,对这方面的辨析不清并没有问题。然而,到了后面的参数估计部分,却可能出现问…...

上游服务不可用了,下游服务如何应对?
上游服务不可用了,下游服务如何应对? 引言 在系统中,上游服务和下游服务是两个关键概念。上游服务通常指的是提供某种功能或数据的服务端,它接收来自下游服务的请求,并根据请求进行处理和响应。下游服务通常指的是发…...

WebGL笔记:矩阵的变换之平移的实现
矩阵的变换 变换 变换有三种状态:平移、旋转、缩放。当我们变换一个图形时,实际上就是在移动这个图形的所有顶点。解释 webgl 要绘图的话,它是先定顶点的,就比如说我要画个三角形,那它会先把这三角形的三个顶点定出来…...

XTU-OJ 1187-Candy
WCB某天买了非常多的糖果并把它们分成N份,依次分别有1,2,3…,N个糖果。他想拿出其中的3份分给他的室友, 为了不让室友们闹意见,必须让这三份的糖果总数恰好能被三人均分。请问他一共有多少种不同的组合方案数ÿ…...
基于 nodejs+vue城市轨道交通线路查询系统mysql
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...
电商时代,VR全景如何解决实体店难做没流量?
近日,电商和实体经济的对立成为了热门话题,尽管电商的兴起确实对线下实体店造成了一定的冲击,但实体店也不是没有办法挽救。VR全景助力线下实体店打造线上店铺,打通流量全域布局,还能实现打开产品、查看产品内部细节等…...
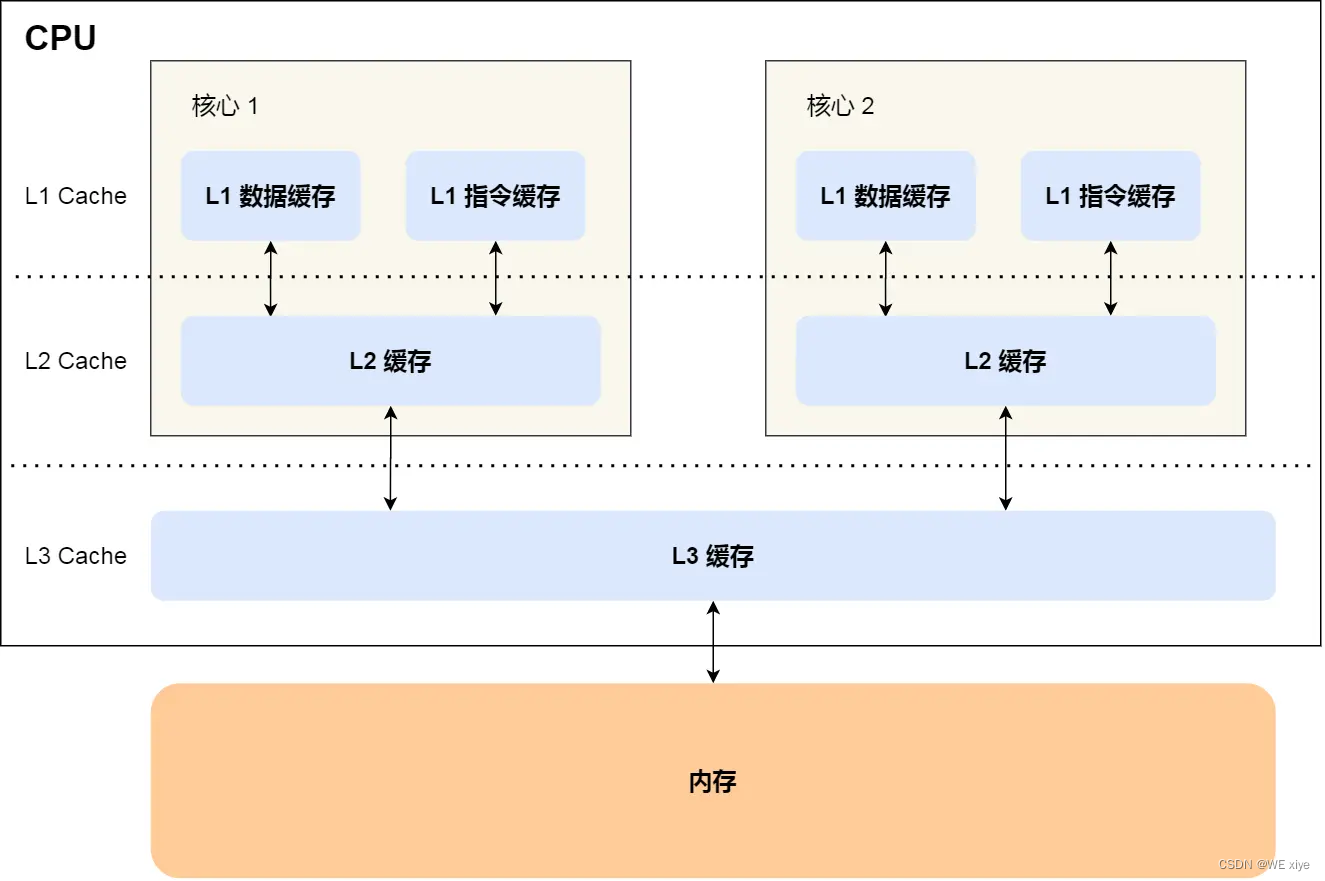
操作系统-浅谈CPU与内存
目录 计算机的基本组成CPU内存虚拟内存内存分段内存分页 CPU与内存的交互过程高速缓存cache 所有图片均来自:小林coding 计算机的基本组成 计算机由软件和硬件组成 硬件由CPU(中央处理器)存储器(内存外存)外部设备组成。 软件由应用软件和系…...
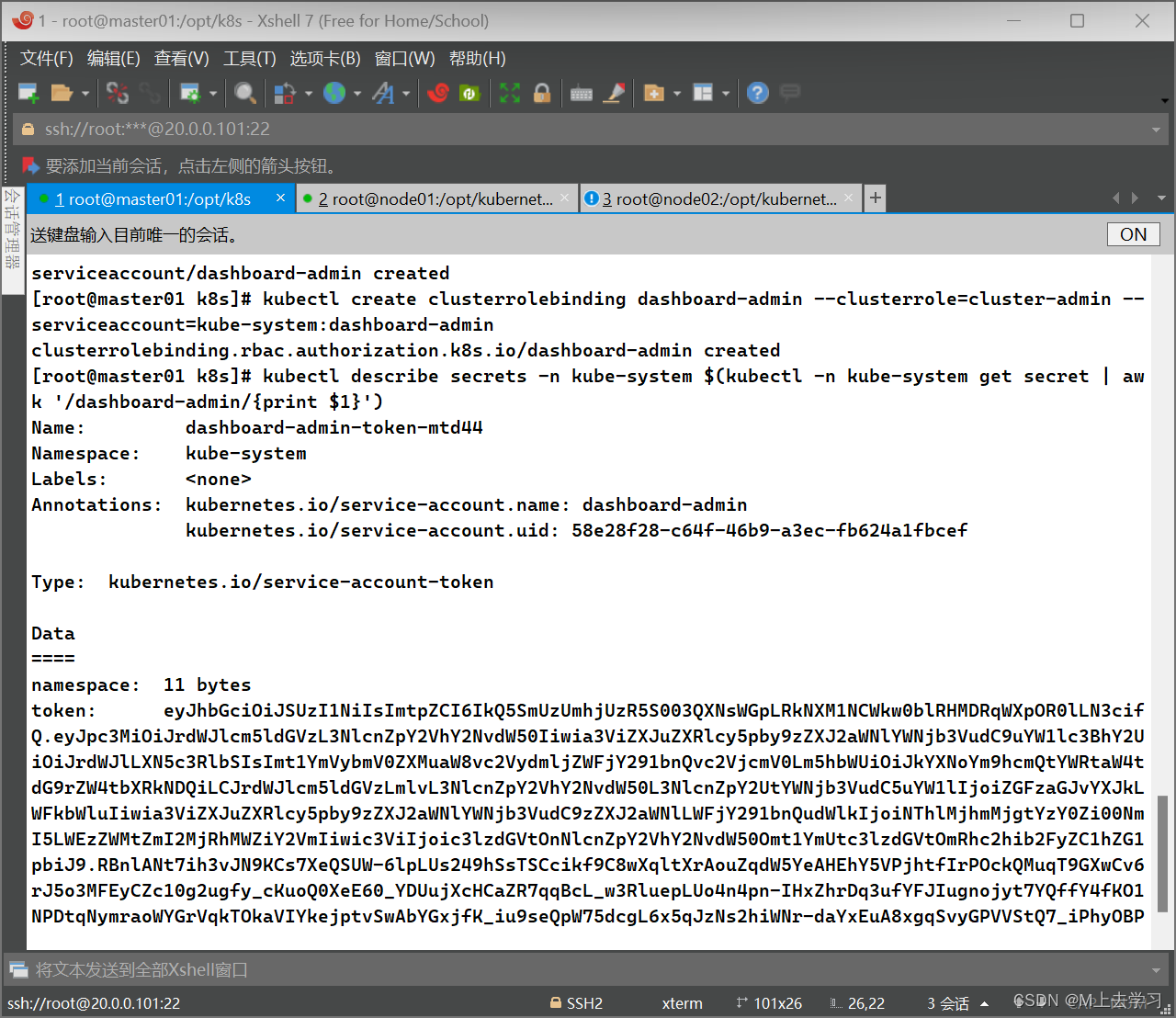
K8s 部署 CNI 网络组件+k8s 多master集群部署+负载均衡
------------------------------ 部署 CNI 网络组件 ------------------------------ ---------- 部署 flannel ---------- K8S 中 Pod 网络通信: ●Pod 内容器与容器之间的通信 在同一个 Pod 内的容器(Pod 内的容器是不会跨宿主机的)共享同一…...
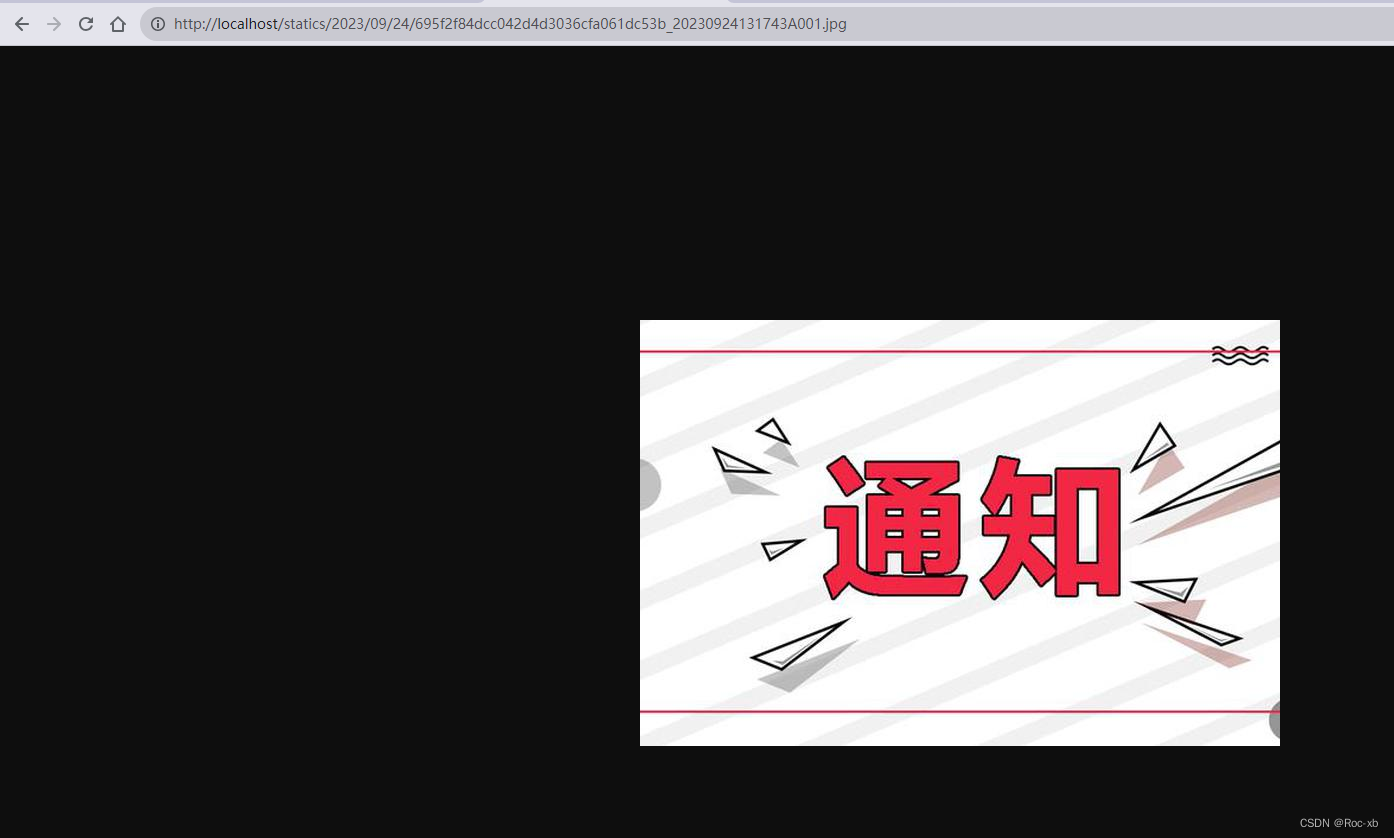
若依微服务上传图片文件代理配置
在使用若依微服务文件上传时候,文件上传成功会上传到D:/ruoyi/uploadPath目录下。默认使用9300端口进行访问图片文件,现在我想把它代理到80端口应该怎么做呢? 配置前:http://localhost:9300/statics/2023/09/24/test.jpg 配置后:http://localhost/statics/2023/09/24/test…...

物联网与 Linux 的相爱相生
Linux 无疑将在物联网中扮演一个关键角色,但是其光彩将与其它的一些分享。 随着 Canonical 重新关注于赢利和新技术,我们中的一些人发现我们正在思考 Linux 未来将走向何方,IoT(物联网)是否是 Linux 的未来࿱…...
:操作浏览器)
python自动化测试(一):操作浏览器
通过Python的代码去操作浏览器的操作 目录 目录 1、导入自动化模块 2、定义打开的浏览器驱动、声明一个url变量保存打开的地址 3、使用函数:driver.get(url)打开浏览器的指定页面 4、最大化浏览器窗口:driver.maximize_window() 5、添加全局的等待…...

NReco.LambdaParser使用案例
使用案例集合: private async void RuleEngine_Click(object sender, EventArgs e){#region 获取变量string expression this.Rule.Text.Trim();string pattern "\$(.*?)\$";MatchCollection matches Regex.Matches(expression, pattern);foreach (Ma…...

苹果IOS安装IPA, plist形式 Safari 浏览器点击安装
快速链接 苹果开发者账号链接 网址: https://developer.apple.com/account 苹果应用上架链接 网址: https://appstoreconnect.apple.com/ 应用证书文件及打包 参考教程: 最新uniapp打包IOS详细步骤(2022) 证书在线制作工具 网址: https://app.121xuexi.…...
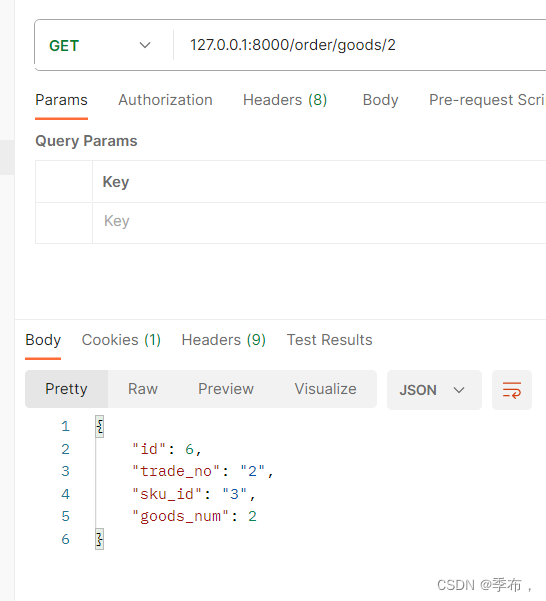
Django 注册及创建订单商品
注册功能的实现 user/views from rest_framework.generics import GenericAPIView from rest_framework.views import APIViewfrom apps.user.models import User from apps.user.serializers import UserSerializer from utils import ResponseMessage from utils.jwt_auth …...

15、Python -- 阶段总结:变量与流程控制
目录 变量变量没有类型,数据有类型 表达式程序流程 变量 变量:编程的本质就是处理数据,数据需要用变量保存 Python语言的特征: 所有变量无需声明,即可使用 变量没有类型 变量没有类型,数据有类型 已学过…...
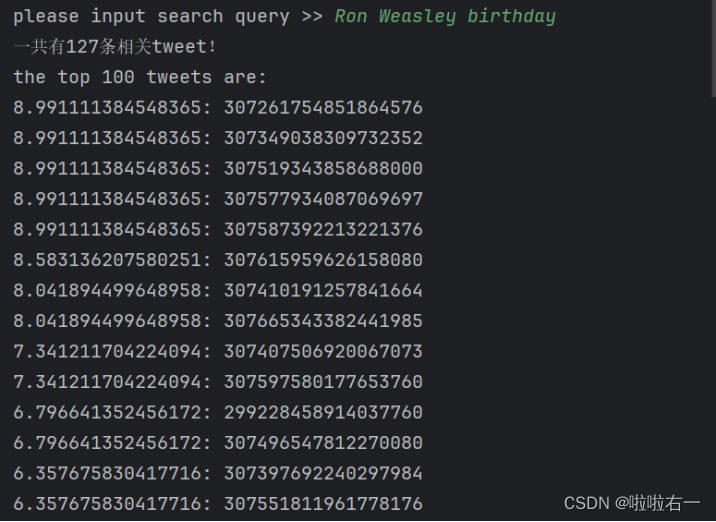
信息检索与数据挖掘 | 【实验】排名检索模型
文章目录 📚实验内容📚相关概念📚实验步骤🐇分词预处理🐇构建倒排索引表🐇计算query和各个文档的相似度🐇queries预处理及检索函数🔥对输入的文本进行词法分析和标准化处理…...

玩转AIGC:打造令人印象深刻的AI对话Prompt
玩转AIGC:打造令人印象深刻的AI对话Prompt 《玩转AIGC:打造令人印象深刻的AI对话Prompt》摘要引言正文良好的Prompt:引发AI深度交流的法宝 ✨探讨不同的提问方式1. 常规提问2. 创意提问 对话交流的艺术:倾听与引导的巧妙平衡 ⚖️…...

uniapp vue国际化 i18n
一、安装 vue-i18n npm i vue-i18n 二、新建i18n目录 1、en.json 内容 {"loginPage":{"namePh":"Please enter your login account","passwordPh":"Please enter password"} } 2、zh-CN.json 内容 {"loginPage&qu…...

Docker 启动远程服务访问不了
今天一下午在弄这个 1、防火墙是否关了 firewall-cmd --state2、ip转发开没开 sysctl net.ipv4.ip_forward3、service iptables是不是打开并拦截了 4、检查docker启动的端口号是否一致,或者启动时对不对 5、检查docker的服务是否起来了,比如你的端口号…...
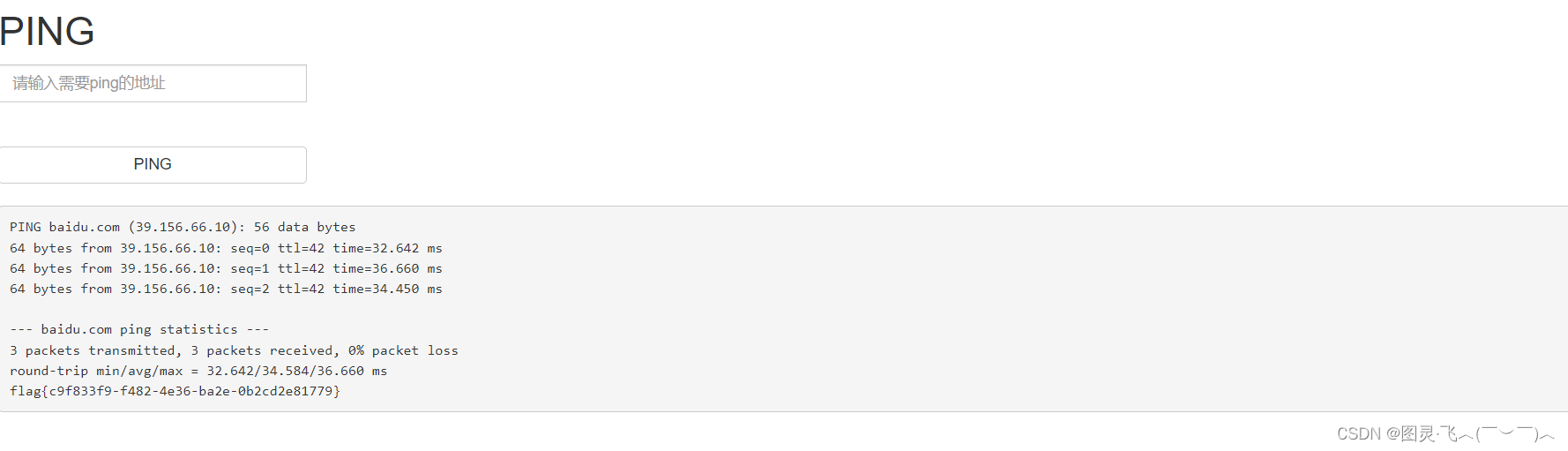
[ACTF2020 新生赛]Exec
【解题过程】 1.打开链接 得到一个能ping 的网站,可以推测这个可以在终端运行的网站。 2.解题思路 在执行的时候我们可以想到命令执行的“;”分号的作用:命令用分号分隔开来,表示它们是两个独立的命令,需要依次执行。…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...
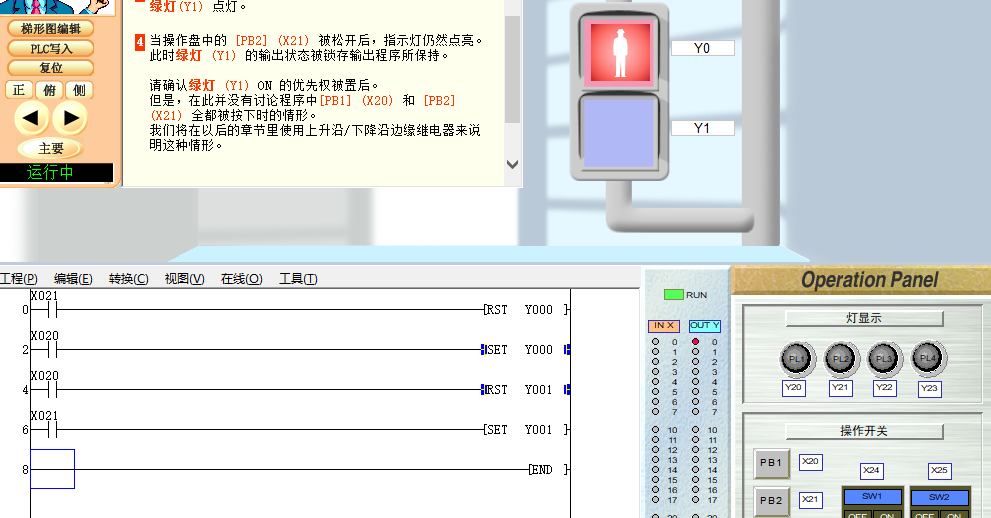
PLC入门【4】基本指令2(SET RST)
04 基本指令2 PLC编程第四课基本指令(2) 1、运用上接课所学的基本指令完成个简单的实例编程。 2、学习SET--置位指令 3、RST--复位指令 打开软件(FX-TRN-BEG-C),从 文件 - 主画面,“B: 让我们学习基本的”- “B-3.控制优先程序”。 点击“梯形图编辑”…...
