矩阵的运算
目标:实现一个能进行稀疏矩阵基本运算(包括加、减、乘)的运算器。
(1)以三元组顺序表表示稀疏矩阵,实现两个矩阵相加、相减、相乘的运算
(2)稀疏矩阵的输入形式为三元组表示,运算结果则以通常的阵列形式列出。
(3)首先提示用户输入矩阵的行数和列数,并判别给出的两个矩阵行、列数对于所要求作的运算是否相匹配。可设矩阵的行数和列数均不超过20。
(4)程序需给出菜单项,用户按照菜单提示进行相应的操作。
#define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>
void menu()
{printf("****************************************************************\n");printf("****************************************************************\n");printf("**********************欢迎使用矩阵计算器************************\n");printf("*******1、转置 2、加法 ******\n");printf("*******3、减法 4、数乘 ******\n");printf("*******5、乘法 0、退出 *******\n");printf("****************************************************************\n");printf("****************************************************************\n");
}void Matrix_output(int(*s)[100], int m, int n)//输出
{int i, j;for (i = 0; i < m; i++){for (j = 0; j < n; j++){printf("%2d ", s[i][j]);}printf("\n");}
}void Matrix_transpose(int(*s)[100], int(*t)[100], int m, int n)//转置
{int i, j;for (i = 0; i < m; i++){for (j = 0; j < n; j++){t[j][i] = s[i][j];}}
}
void Matrix_addition(int(*s)[100], int(*t)[100], int(*p)[100], int m, int n)//相加
{int i, j;for (i = 0; i < m; i++){for (j = 0; j < n; j++){p[i][j] = s[i][j] + t[i][j];}}
}void Matrix_subtraction(int(*s)[100], int(*t)[100], int(*p)[100], int m, int n)//相减
{int i, j;for (i = 0; i < m; i++){for (j = 0; j < n; j++){p[i][j] = s[i][j] - t[i][j];}}
}void Matrix_shucheng(int(*s)[100], int(*t)[100], int m, int n, int k)//数乘
{int i, j;for (i = 0; i < m; i++){for (j = 0; j < n; j++){t[i][j] = k * s[i][j];}}
}void Matrix_multiplication(int(*s)[100], int(*t)[100], int(*p)[100], int m, int n, int x, int y)//相乘
{int i, j, k, sum;for (i = 0; i < m; i++){for (j = 0; j < y; j++){sum = 0;for (k = 0; k < n; k++){sum += s[i][k] * t[k][j];}p[i][j] = sum;}}
}int main()
{int m, n, i, j, k, input;int x, y;int A[100][100], B[100][100], C[100][100];do{menu();printf("请选择:>");scanf("%d", &input);switch (input){case 1://转置printf("请输入矩阵的行数:> ");scanf("%d", &m);printf("\n");printf("请输入矩阵的列数:> ");scanf("%d", &n);printf("\n");printf("请输入矩阵:\n");for (i = 0; i < m; i++){for (j = 0; j < n; j++){scanf("%d", &A[i][j]);}}printf("原矩阵:\n");Matrix_output(A, m, n);Matrix_transpose(A, B, m, n);printf("转置后的矩阵:\n");Matrix_output(B, n, m);break;case 2://相加printf("请输入第一个矩阵的行数:> ");scanf("%d", &m);printf("\n");printf("请输入第一个矩阵的列数:> ");scanf("%d", &n);printf("\n");printf("请输入矩阵:\n");for (i = 0; i < m; i++){for (j = 0; j < n; j++){scanf("%d", &A[i][j]);}}printf("请输入第二个矩阵的行数:> ");scanf("%d", &x);printf("\n");printf("请输入第二个矩阵的列数:> ");scanf("%d", &y);printf("\n");if (m == x && n == y){printf("请输入矩阵:\n");for (i = 0; i < m; i++){for (j = 0; j < n; j++){scanf("%d", &B[i][j]);}}printf("第一个矩阵:\n");Matrix_output(A, m, n);printf("第二个矩阵:\n");Matrix_output(B, m, n);Matrix_addition(A, B, C, m, n);printf("和矩阵:\n");Matrix_output(C, m, n);}else{printf("这两个矩阵不是同型矩阵,不能相加\n");}break;case 3:printf("请输入第一个矩阵的行数:> ");scanf("%d", &m);printf("\n");printf("请输入第一个矩阵的列数:> ");scanf("%d", &n);printf("\n");printf("请输入第一个矩阵:\n");for (i = 0; i < m; i++){for (j = 0; j < n; j++){scanf("%d", &A[i][j]);}}printf("请输入第二个矩阵的行数:> ");scanf("%d", &x);printf("\n");printf("请输入第二个矩阵的列数:> ");scanf("%d", &y);printf("\n");if (m == x && n == y){printf("请输入第二个矩阵:\n");for (i = 0; i < m; i++){for (j = 0; j < n; j++){scanf("%d", &B[i][j]);}}printf("第一个矩阵:\n");Matrix_output(A, m, n);printf("第二个矩阵:\n");Matrix_output(B, m, n);Matrix_subtraction(A, B, C, m, n);printf("差矩阵:\n");Matrix_output(C, m, n);}else{printf("这两个矩阵不是同型矩阵,不能相减\n");}break;case 4:printf("请输入矩阵的行数:> ");scanf("%d", &m);printf("\n");printf("请输入矩阵的列数:> ");scanf("%d", &n);printf("\n");printf("请输入这个数:>");scanf("%d", &k);printf("\n");printf("请输入矩阵:\n");for (i = 0; i < m; i++){for (j = 0; j < n; j++){scanf("%d", &A[i][j]);}}printf("原矩阵:\n");Matrix_output(A, m, n);Matrix_shucheng(A, B, m, n, k);printf("数乘矩阵:\n");Matrix_output(B, m, n);break;case 5:printf("请输入第一个矩阵的行数:> ");scanf("%d", &m);printf("\n");printf("请输入第一个矩阵的列数:> ");scanf("%d", &n);printf("\n");printf("请输入第一个矩阵:\n");for (i = 0; i < m; i++){for (j = 0; j < n; j++){scanf("%d", &A[i][j]);}}printf("请输入第二个矩阵的行数:> ");scanf("%d", &x);printf("\n");printf("请输入第二个矩阵的列数:> ");scanf("%d", &y);printf("\n");if (n == x){printf("请输入第二个矩阵:\n");for (i = 0; i < x; i++){for (j = 0; j < y; j++){scanf("%d", &B[i][j]);}}printf("第一个矩阵:\n");Matrix_output(A, m, n);printf("第二个矩阵:\n");Matrix_output(B, x, y);Matrix_multiplication(A, B, C, m, n, x, y);printf("相乘矩阵:\n");Matrix_output(C, m, y);}else{printf("这两个矩阵不能相乘\n");}break;case 0:printf("退出计算,欢迎再次使用\n");break;default:printf("输入错误,请从新输入\n");break;}} while (input);return 0;
}出菜单项,用户按照菜单提示进行相应的操作。
相关文章:

矩阵的运算
目标:实现一个能进行稀疏矩阵基本运算(包括加、减、乘)的运算器。 (1)以三元组顺序表表示稀疏矩阵,实现两个矩阵相加、相减、相乘的运算 (2)稀疏矩阵的输入形式为三元组表示,运算结果则以通常…...

Android 获取SIM卡号码权限申请
1.添加权限 在AndroidManifest.xml中添加如下权限 <uses-permission android:name"android.permission.READ_PHONE_STATE"/> 2.获取权限 如果你只在清单文件中添加权限却没有在代码中获取权限,代码还是会报错的。 报错原因: android…...

Linux CentOS 本地yum配置
本地开发用虚拟机,因为有光盘镜像在手,并不需要联网安装组件,只需要设置一下就可以让yum从本地获取源。 将安装盘挂载在合适位置 mount /dev/cdrom /mnt 进入目录 cd /etc/yum.repos.d/ 修改CentOS-Media.repo里面的挂载路径 …...

【c++速通】入门级攻略:什么是内联函数?函数重载又是什么?
🎥 屿小夏 : 个人主页 🔥个人专栏 : C入门到进阶 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言🌤️函数重载☁️函数重载的概念☁️函数重载的作用☁️C支持函数重载的原理…...

ubuntu 安装串口工具和添加虚拟串口
目录 一、串口工具安装 二、使用Windows本身虚拟的串口 (一)添加串口 1、保证虚拟机是关闭状态,打开“虚拟机设置”,点击“添加”。 2、选中“串行端口”,点击“完成”。 3、选中刚添加的串口,下拉选…...
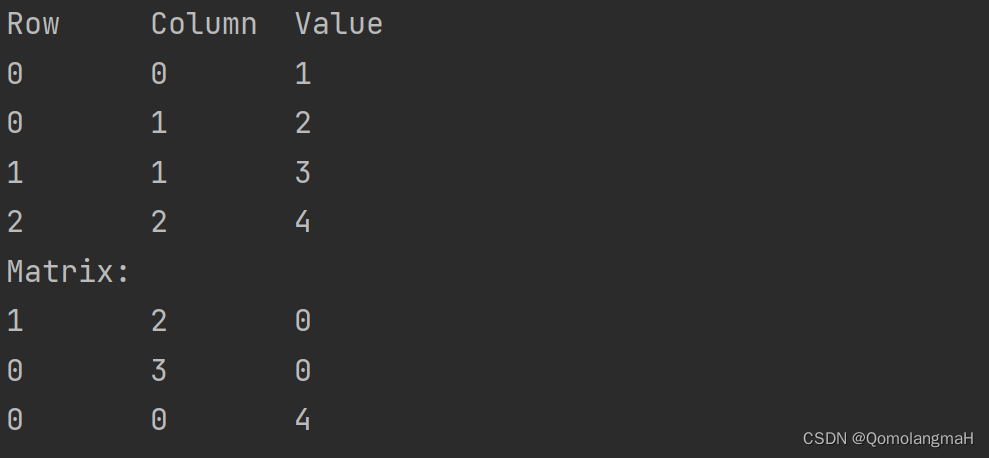
【数据结构】数组和字符串(四):特殊矩阵的压缩存储:稀疏矩阵——三元组表
文章目录 4.2.1 矩阵的数组表示4.2.2 特殊矩阵的压缩存储a. 对角矩阵的压缩存储b~c. 三角、对称矩阵的压缩存储d. 稀疏矩阵的压缩存储——三元组表结构体初始化元素设置打印矩阵主函数输出结果代码整合 4.2.1 矩阵的数组表示 【数据结构】数组和字符串(一ÿ…...

为什么POST请求经常发送两次?
大多数初级前端程序员,在通过浏览器F12的调试工具调试网络请求时,可能都会有一个发现,在进行POST请求时,明明代码里只请求了一次,为什么network里发送了两次呢,难道我代码出bug了?带着疑问点开第…...

打破总分行数据协作壁垒,DataOps在头部股份制银行的实践|案例研究
从银行开始建设数据仓库至今已近20年,当前各银行机构在数据能力建设中面临诸多困扰:如何保证数据使用时的准确性?如何让数据敏捷响应业务变化?如何让更多的业务人员使用数据? 这些问题极大影响了经营指标的达成与业务…...
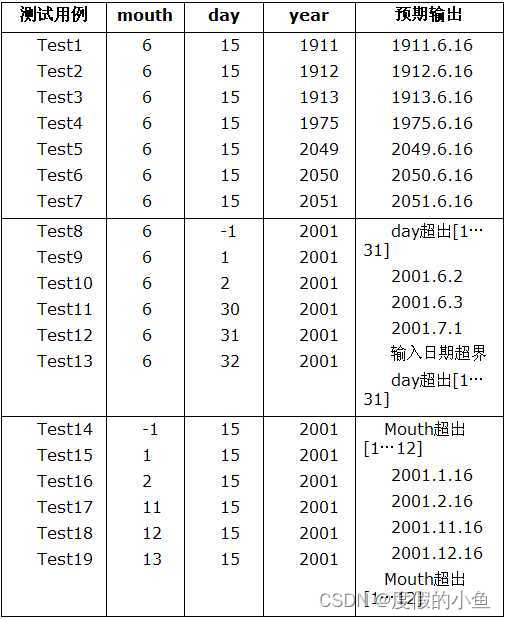
测试用例的设计方法(全):边界值分析方法
一.方法简介 1.定义:边界值分析法就是对输入或输出的边界值进行测试的一种黑盒测试方法。通常边界值分析法是作为对等价类划分法的补充,这种情况下,其测试用例来自等价类的边界。 2.与等价划分的区别 1)边界值分析不是从某等价类中随便挑…...
酷开科技 | 酷开系统沉浸式大屏游戏更解压!
随着家庭娱乐需求日益旺盛,越来越多的家庭消费者和游戏玩家开始追求大屏游戏带来的沉浸感。玩家在玩游戏的时候用大屏能获得更广阔的视野和更出色的视觉包围感,因此用大屏玩游戏已经成为了一种潮流。用酷开系统玩大屏游戏,过瘾又刺激…...
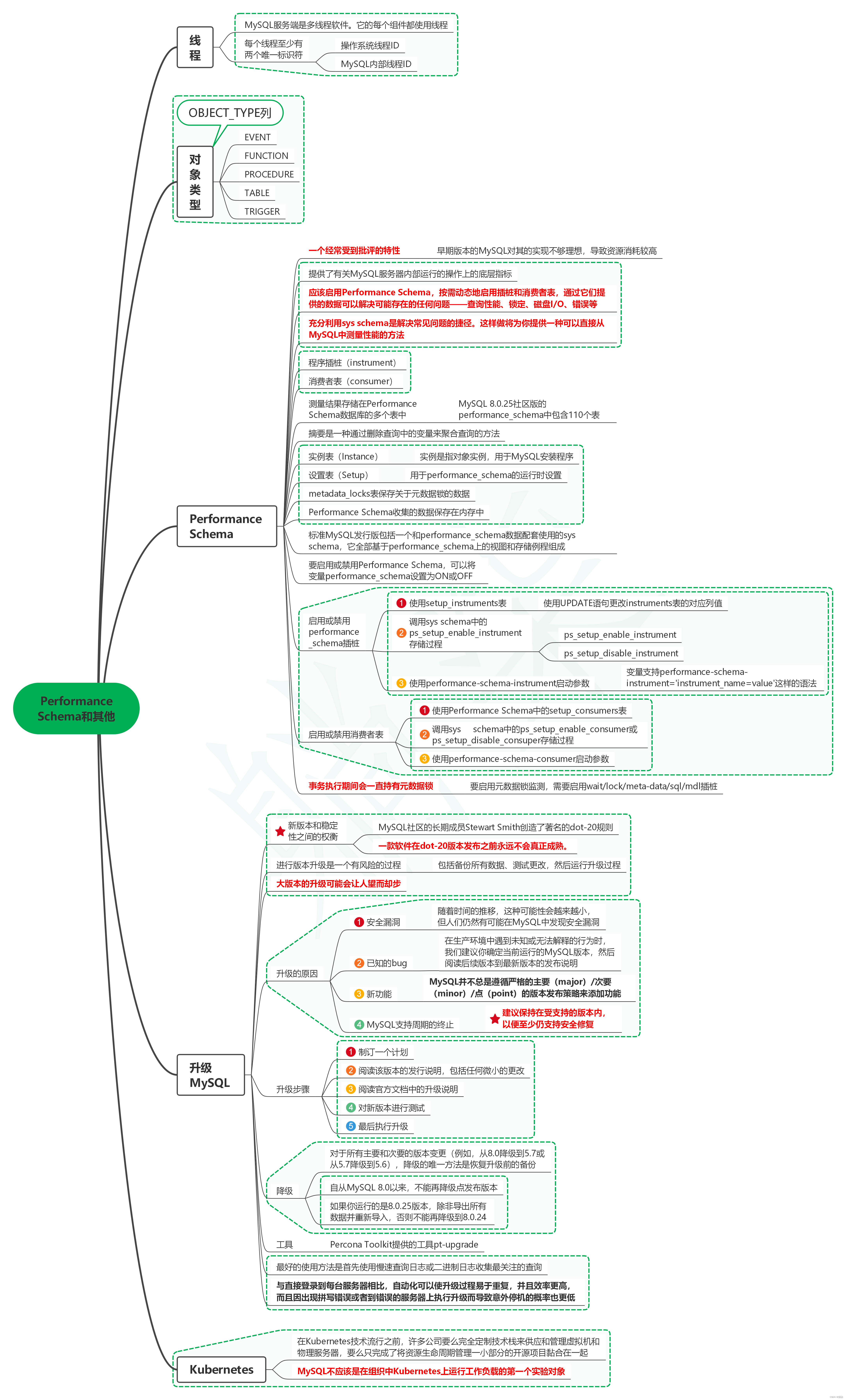
读高性能MySQL(第4版)笔记20_Performance Schema和其他
1. 线程 1.1. MySQL服务端是多线程软件。它的每个组件都使用线程 1.2. 每个线程至少有两个唯一标识符 1.2.1. 操作系统线程ID 1.2.2. MySQL内部线程ID 2. 对象类型 2.1. OBJECT_TYPE列 2.2. EVENT 2.3. FUNCTION 2.4. PROCEDURE 2.5. TABLE 2.6. TRIGGER 3. Perfor…...
《二》)
spring cloud Eureka集群模式搭建(IDEA中运行)《二》
上一篇集群配置文件完善 上一篇博客,想必大家都学会了Eureka集群模式的搭建和运行,针对上一篇的配置文件进行了优化,在这里分享给大家。上一篇主要有3个配置文件,分别对应3个不同的服务,这种形式配置文件分别写在了不…...

大模型(LLM)在电商推荐系统的探索与实践
本文对LLM推荐的结合范式进行了梳理和讨论,并尝试将LLM涌现的能力迁移应用在推荐系统之中,利用LLM的通用知识来辅助推荐,改善推荐效果和用户体验。 背景 电商推荐系统(Recommend System,RecSys)是一种基于…...
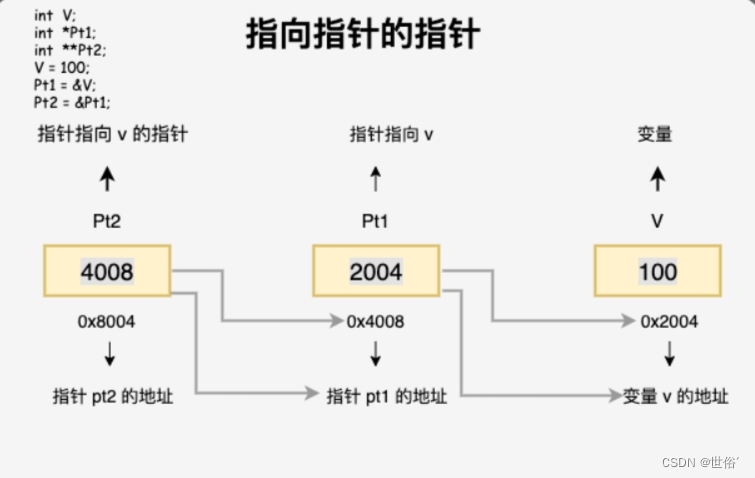
C语言之指针详解
目录 地址 指针的定义和使用 数组与指针的区别与联系 字符串与指针的用法 C 中的 NULL 指针 指针的算术运算 指向指针的指针 传递指针给函数 从函数返回指针 在学习指针之前,我们先弄清楚一个概念: 地址 地址在计算机内存中是一个唯一的标识符…...
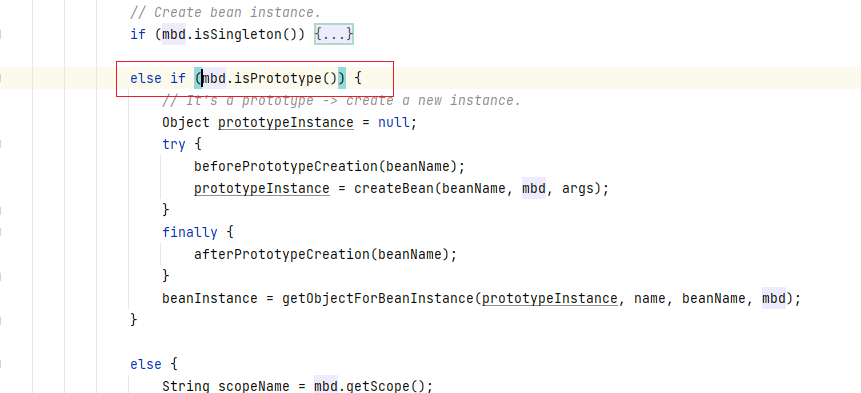
【Java笔记+踩坑】设计模式——原型模式
导航: 【Java笔记踩坑汇总】Java基础JavaWebSSMSpringBootSpringCloud瑞吉外卖/黑马旅游/谷粒商城/学成在线设计模式面试题汇总性能调优/架构设计源码-CSDN博客 目录 零、经典的克隆羊问题(复制10只属性相同的羊) 一、传统方案࿱…...

Flutter GetX使用详解
介绍 GetX是一款功能强大且轻量级的Flutter状态管理和路由管理库。它提供了一种简单而强大的方式来构建Flutter应用程序,无需大量的模板代码。GetX不仅提供了状态管理和路由管理,还包括其他实用工具,如国际化和依赖注入。 在本文中…...

【ARM Coresight 系列文章 3.3 - ARM Coresight SWD 协议详细介绍】
文章目录 1.1 SWD 协议框图1.2 读/写时序及命令1.2.1 SWD 时序1.2.2 SWD 命令详情1.3 芯片探测1.3.1 获取芯片 ID1.4 读/写操作1.1 SWD 协议框图 SWD协议可以配置SoC内部几乎所有的寄存器。时钟信号由SWCLK 管脚输入,数据信号从SWDIO管脚输入输出。首先 HOST 对SW-DP 进行操作…...

作为开发者,可视化开发工具了解一下
你是否为编程世界的各种挑战感到头痛?想要以更高效、简单的方式开发出专业级的项目? JNPF低代码工具正是你苦心寻找的产品!它是一款专为稍微懂一点点编程思想的入门级人员设计的神奇工具,集成了丰富的功能和组件,让你轻…...

Python:实现日历功能
背景 日常生活中,每天都要用到日历,日历成为我们生活中的必需品,那么如何制作日历呢,其实方法有很多,可以直接在excel中制作,也可以手画等等。 学习过编程的朋友,能否想到用Python编写一…...
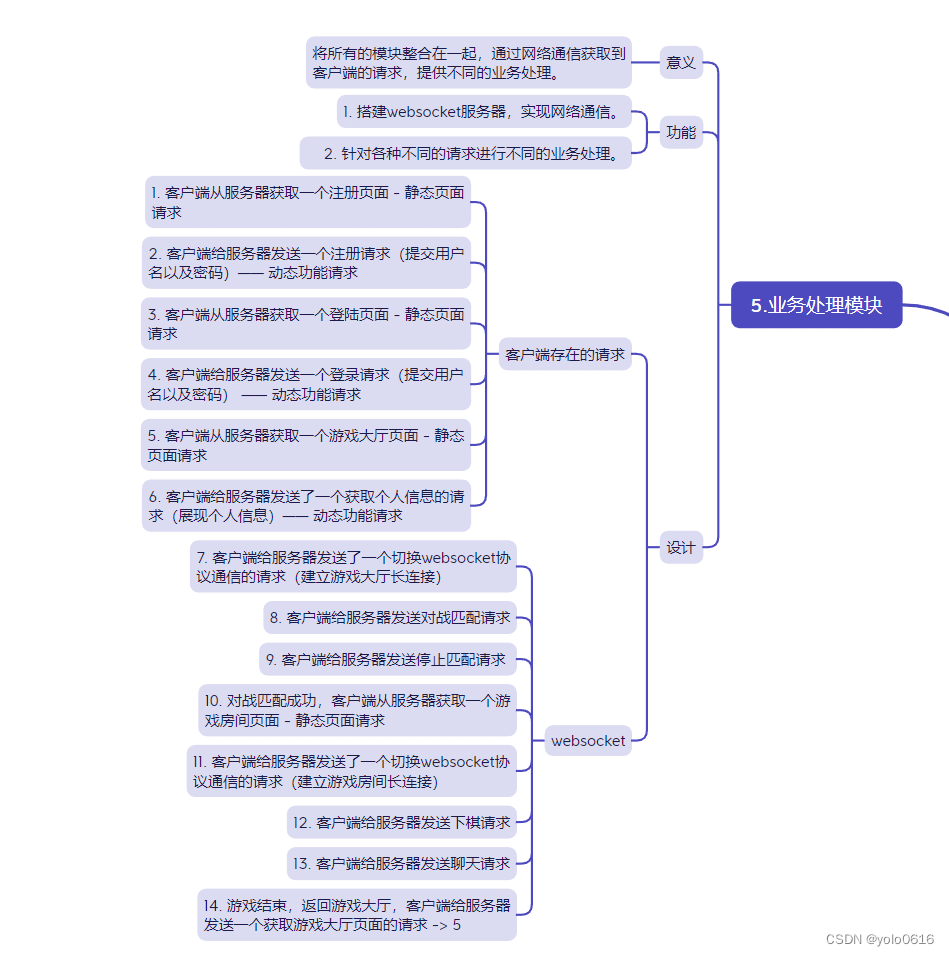
2.9.C++项目:网络版五子棋对战之业务处理模块的设计
文章目录 一、意义二、功能三、管理(一)客户端请求(二)websocket 四、框架五、完整代码 一、意义 将所有的模块整合在一起,通过网络通信获取到客户端的请求,提供不同的业务处理。 服务器模块,是…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
