Python中的文件操作和异常处理
在Python编程中,文件操作和异常处理是非常重要的概念。本文将介绍如何使用Python进行文件读写操作,并展示如何处理可能出现的错误和异常情况。
文件读写操作
Python提供了简单而强大的文件读写功能,让我们能够轻松地处理各种文件类型。下面是一些常见的文件操作示例:
1、打开文件
使用open()函数可以打开一个文件,并返回一个文件对象。可以指定文件名和打开模式(读取、写入、追加等)。
file = open("data.txt", "r") # 以只读模式打开名为"data.txt"的文件2、读取文件内容
可以使用文件对象的read()方法来读取文件的内容。
content = file.read() # 读取整个文件内容
print(content)
3、写入文件内容
使用文件对象的write()方法可以将数据写入文件。
file.write("Hello, World!") # 将字符串写入文件4、关闭文件
在完成文件操作后,应该关闭文件对象,释放系统资源。
file.close() # 关闭文件异常处理
在编程过程中,可能会出现各种错误和异常。Python提供了异常处理机制,让我们能够优雅地处理这些异常情况。下面是一些常见的异常处理示例:
1、捕获异常
使用try-except语句可以捕获并处理异常。在try块中编写可能引发异常的代码,在except块中处理异常情况。
try:# 可能引发异常的代码file = open("data.txt", "r")content = file.read()print(content)
except FileNotFoundError:# 处理文件不存在的异常print("文件不存在!")
2、处理多个异常
可以使用多个except块来处理不同类型的异常。
try:# 可能引发异常的代码file = open("data.txt", "r")content = file.read()print(content)
except FileNotFoundError:# 处理文件不存在的异常print("文件不存在!")
except PermissionError:# 处理权限错误的异常print("没有访问权限!")
except:# 处理其他异常print("发生了未知错误!")
3、最终执行代码
使用finally块可以编写在无论是否发生异常时都会执行的代码。
try:# 可能引发异常的代码file = open("data.txt", "r")content = file.read()print(content)
except FileNotFoundError:# 处理文件不存在的异常print("文件不存在!")
finally:# 最终执行的代码file.close()
通过合理地使用文件操作和异常处理,我们可以更好地处理数据和错误,使我们的代码更加健壮和可靠。
相关文章:

Python中的文件操作和异常处理
在Python编程中,文件操作和异常处理是非常重要的概念。本文将介绍如何使用Python进行文件读写操作,并展示如何处理可能出现的错误和异常情况。 文件读写操作 Python提供了简单而强大的文件读写功能,让我们能够轻松地处理各种文件类型。下面…...

KF-GINS 和 OB-GINS 的 Earth类 和 Rotation 类
原始 Markdown文档、Visio流程图、XMind思维导图见:https://github.com/LiZhengXiao99/Navigation-Learning 文章目录 一、Earth 类:地球参数和坐标转换1、gravity():正常重力计算2、meridianPrimeVerticalRadius():计算子午圈半径…...

2017年亚太杯APMCM数学建模大赛B题喷雾轨迹规划问题求解全过程文档及程序
2017年亚太杯APMCM数学建模大赛 B题 喷雾轨迹规划问题 原题再现 喷釉工艺用喷釉枪或喷釉机在压缩空气下将釉喷入雾中,使釉附着在泥体上。这是陶瓷生产过程中一个容易实现自动化的过程。由于不均匀的釉料在烧制过程中会产生裂纹,导致工件报废࿰…...

柏拉图式爱情是同性之爱,绘画是理念世界的二次模仿
公元前427年,柏拉图出生在雅典。 柏拉图20岁成为苏格拉底的弟子。 有一次,柏拉图问苏格拉底:“什么是爱情?”苏格拉底说:“请穿越麦田,摘一株最大最金黄的麦穗回来。不走回头路,只能摘一次。”…...

【滴滴出行安全应急响应平台DSRC2倍积分卡】
1、使用方法 2、券(记得点个关注,做一下数据)...

HashMap 元素添加流程
在Java 1.8中,HashMap的元素添加流程: 计算键的哈希值:当调用put(key, value)方法时,首先会计算键(key)的哈希值,这个哈希值用来确定元素在内部数组中的位置。确定位置:通过哈希值&…...

甲亢_甲状腺功能亢进_Methimazole甲巯基咪唑
美国医生 Methimazole甲巯基咪唑 is used to treat hyperthyroidism, a condition where the thyroid gland produces too much thyroid hormone. It is also used before thyroid surgery or radioactive iodine treatment. Methimazole is an antithyroid medicine. It wor…...
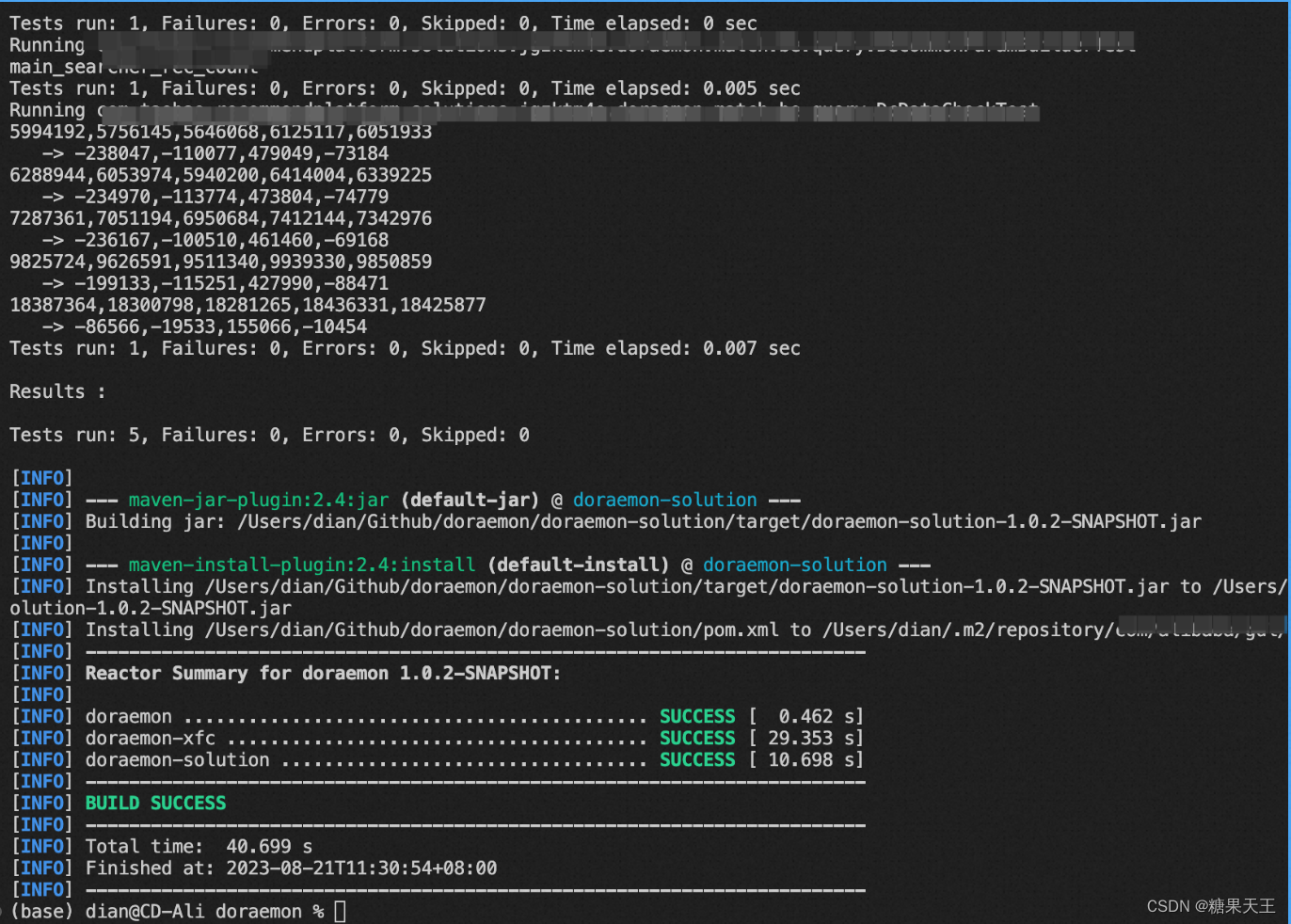
【Maven】VSCode Java+Maven 环境配置
0x00 前言 没写过 Java,得配个带 Maven 的编码环境,不太明白,试试看顺便记录一下 0x01 配置过程 安装 jdk1.8 后,找到安装位置: (base) dianCD-Ali doraemon % /usr/libexec/java_home -V Matching Java Virtual Ma…...

【目标检测】非极大值抑制NMS的原理与实现
非极大值抑制(Non-Maximum Suppression,NMS)是目标检测中常用的一种技术,它的主要作用是去除冗余和重叠过高的框,并保留最佳的几个。 NMS计算的具体步骤如下: 首先根据目标检测模型输出结果,得…...

应用程序架构是如何演变的
【squids.cn】 全网zui低价RDS,免费的迁移工具DBMotion、数据库备份工具DBTwin、SQL开发工具等 如果您一直在开发或以某种方式参与应用程序架构,那么在过去的几年中您肯定看到了许多变化。有很多不同类型的架构和技术陆续出现然后消失,以至于…...

云原生Docker Cgroups资源控制操作
目录 资源控制 cgroups四大功能 CPU 资源控制 设置CPU使用率上限 进行CPU压力测试 设置50%的比例分配CPU使用时间上限 设置CPU资源占用比(设置多个容器时才有效) 设置容器绑定指定的CPU 对内存使用的限制 限制容器可以使用的最大内存 限制可用的…...

【Java集合类面试二十五】、有哪些线程安全的List?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:有哪些线程安全的List&a…...
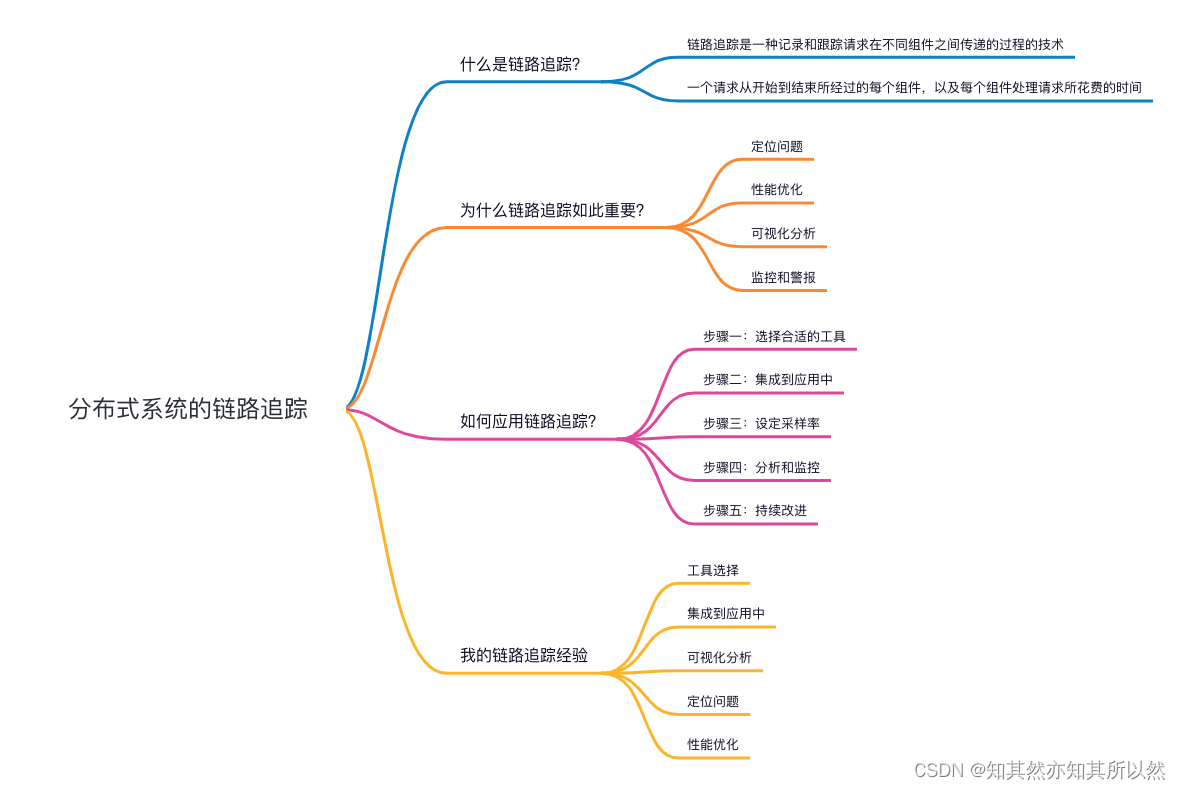
分布式系统的链路追踪,让你轻松解决订单无法查看的问题!
你好,我是积极活泼的小米!今天我要跟大家聊聊分布式系统的链路追踪,这个话题对于我们在技术领域工作的小伙伴们来说,可是非常重要的哦! 背景 昨天,产品大佬丰哥找到了我,他抱怨说分销员的订单…...

基于生产数据测试设计、测试回归
问题背景 QA搬砖日常中,你会不会有这样的问题,测试设计时有些场景没考虑到,上线就因为测试中没覆盖到的场景而导致缺陷溢出。从缺陷分类统计来看,类似这样的例子占比是很高的。 解决措施 仅依靠测试者设置的场景,模拟…...

装了mac os 14.0 sonoma 在腾讯会议投屏时候,无法设置麦克风权限问题
愿意:界面上直接空白的,无法手动或自动弹出要配置授权的软件 解决思路: 给 TCC.db 增加1条权限记录 添加到数据库里 /usr/bin/sqlite3 ~/Library/Application\ Support/com.apple.TCC/TCC.db "INSERT INTO main.access (service, cli…...

ARM 汇编指令 orreq 的使用
orreq 阅读代码时,发现有个【组合指令】 orreq, orr 一般是 OR,也就是或操作,后面加个 eq 表示什么呢? 比如下面的代码:前面一个操作, tst,好像没做实际的操作,可能影响…...
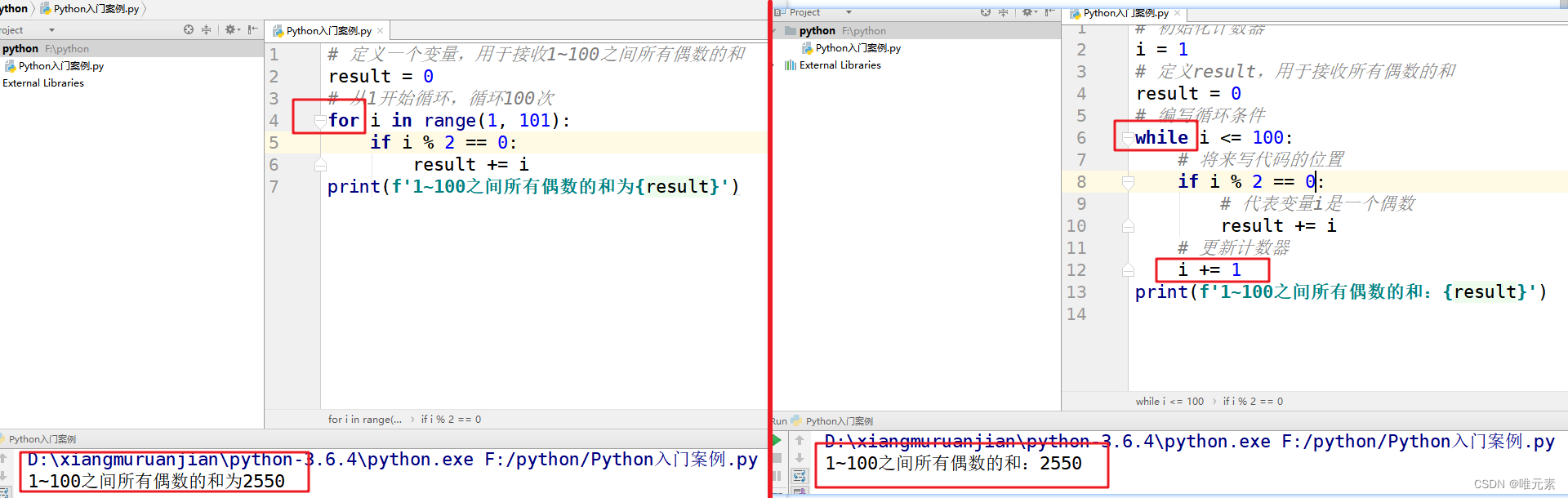
Python---练习:for循环 求1-100的和/所有偶数的和
案例: 使用for循环,求1 ~ 100的和 之前用while循环,做过算出1--100的和。 相关链接: Python--练习:使用while循环求1..100的和-CSDN博客 结合着看看for循环怎么实现。 思考: 先把for循环的基本语法写…...

APP逆向基础(APK流程)
APK的基本结构 Android体系结构和APK基本结构-CSDN博客 APK 打包流程 【Android 安装包优化】APK 打包流程 ( 文件结构 | 打包流程 | 安装流程 | 安卓虚拟机 )_adnroid 安装包优化,打指定资源_韩曙亮的博客-CSDN博客 APK安装流程...

Tomcat调试端口被占用解决办法
Tomcat调试端口被占用解决办法 tomcat启动报错: Unable to open debugger port (127.0.0.1:52718): java.net.BindException "Address already in use: NET_Bind"这个错误表明Tomcat服务器在启动时尝试打开调试端口(通常是在调试模式下使用的…...
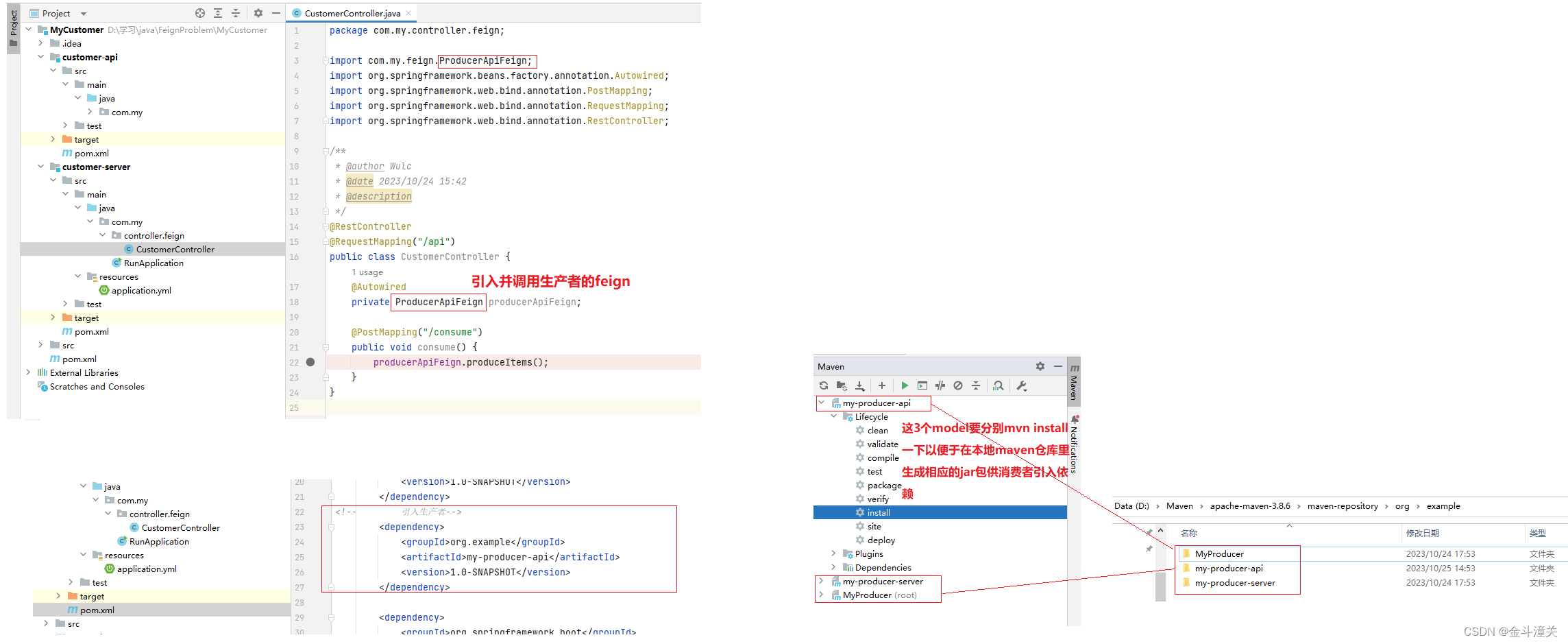
feign之间相互通信RequestInterceptor拦截器失效
1、问题描述 前段时间碰到一个问题,有两个服务A和服务B,通过feign进行通信。因为feign之间无法直接传递请求头,只能传请求体。因此需要借助RequestInterceptor拦截器获取到请求头。服务B中设置了RequestInterceptor拦截器,但是在A…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
