当前位置： 首页 > news >正文

计算机视觉-数学基础*变换域表示

news 2026/2/9 15:09:50

被研究最多的图像（或任何序列数据）变换域表示是通过傅 里叶分析 。所谓的傅里叶表示就是使用
正弦函数的线性组合来表示信号。对于一个给定的图像I(n1,n2) ，可以用如下方式分解它（即逆傅里叶变换）：
其中，I F(u,v) 是傅里叶系数，可以由如下方式（即傅里叶变换）得到：
在这种表示中，像素表示的图像 I(n1,n2)被分解成频率分量。每个频率分量的系数描述该频率分量存在的多少 频率分量在这里成为表示图像的基础。这种方法的常见应用是 JPEG (] o in t Photographic Experts Group )图像压缩中用到的可变离散余弦变换（ Discrete Cosine Transform, DCT JPE 编解码器仅使用式 (1.2) 中正弦曲线的余弦分量，因 此称为 离散余弦基 DCT 基函数如图 所示1-2所示
从像素表示到变换域表示的任何变换核都可以写成 b(n1,n2.u,v) ，逆向 变换写成的B (n1,n2.u,v) 对于许多变换，这些基在数学上通常是可逆的，相 互之间可 以转换 从图像空间到基空间的映射或变换可以公式化为：
式（1.3）是式（1.2）的一般化。许多图像表示可以通过这种形式在变换域建模，傅里叶变换只是其中的一种特殊情况

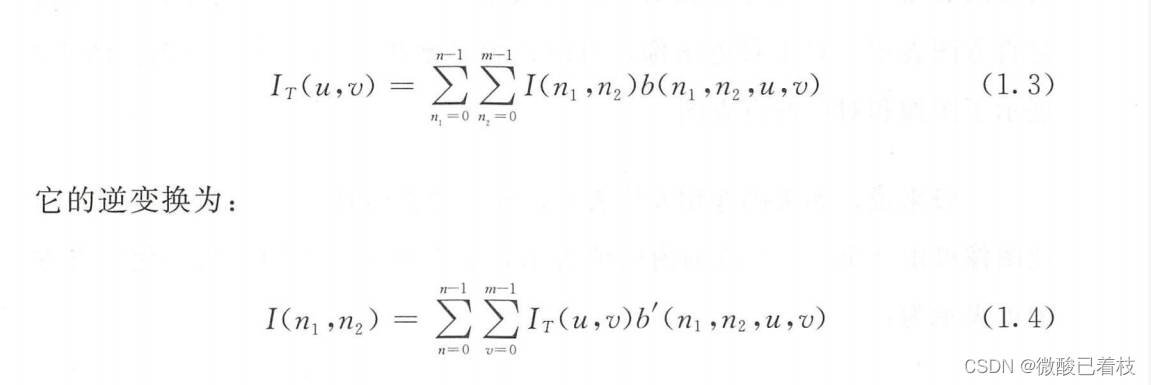
相关文章：

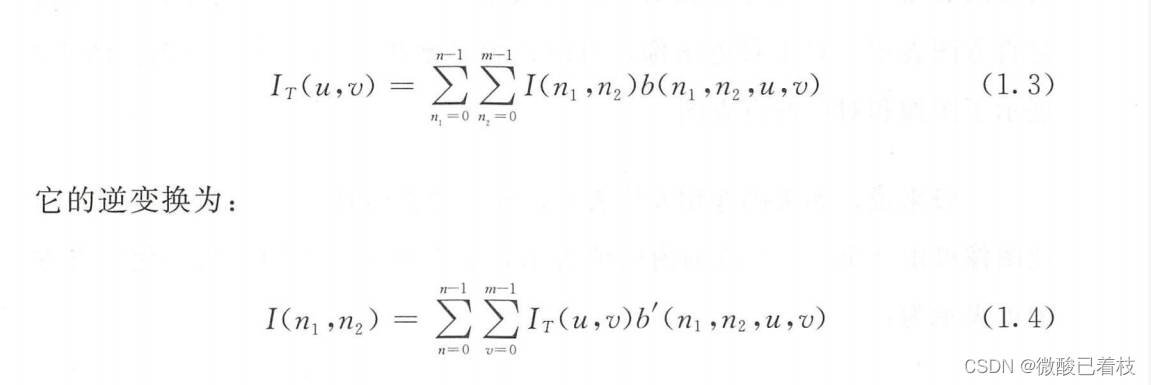
计算机视觉-数学基础*变换域表示

被研究最多的图像（或任何序列数据）变换域表示是通过傅 里叶分析 。所谓的傅里叶表示就是使用 正弦函数的线性组合来表示信号。对于一个给定的图像I(n1,n2) ，可以用如下方式分解它（即逆傅里叶变换）： 其中&a…...

编程日记 2023/10/26 13:56:37

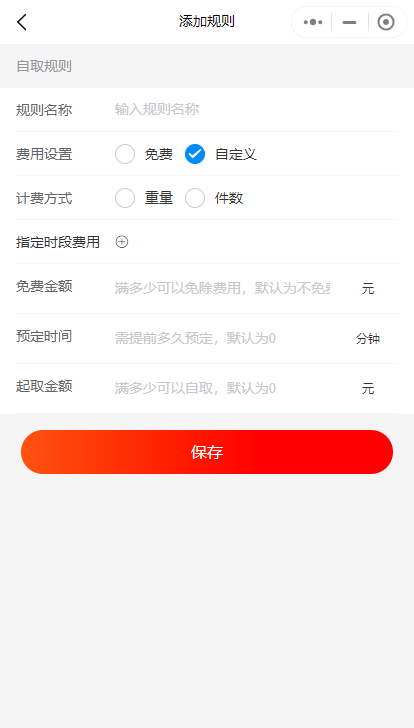
小程序如何设置自取规则

​在小程序中，自取规则是指当客户下单时选择无需配送的情况下，如何设置相关的计费方式、指定时段费用、免费金额、预定时间和起取金额。下面将详细介绍如何设置这些规则，以便更好地满足客户的需求。 在小程序管理员后台->配送设置->自…...

编程日记 2023/10/26 13:55:36

Elasticsearch分词器-中文分词器ik

文章目录 使用standard analysis对英文进行分词使用standard analysis对中文进行分词安装插件对中文进行友好分词-ik中文分词器下载安装和配置IK分词器使用ik_smart分词器使用ik_max_word分词器 借助Nginx实现ik分词器自定义分词网络新词 ES官方文档Text Analysis 使用standard…...

编程日记 2023/10/26 13:54:33

ITSS信息技术服务运行维护标准符合性证书申请详解及流程

ITSS信息技术服务运行维护标准符合性证书 认证介绍 ITSS（InformationTechnologyServiceStandards,信息技术服务标准，简称ITSS)是一套成体系和综合配套的信息技术服务标准库，全面规范了IT服务产品及其组成要素，用于指导实施标准化…...

编程日记 2023/10/26 13:53:32

Inbound marketing的完美闭环：将官网作为营销枢纽,从集客进化为入站

Inbound marketing即入站营销的运作方式不同于付费广告，你需要不断地投入才能获得持续的访问量。而你的生意表达内容一经创建、发布，就能远远不断地带来流量。 Inbound marketing也被翻译作集客营销，也就是美国知名的营销SaaS企业hubspot所主…...

编程日记 2023/10/26 13:52:31

SQL On Pandas最佳实践

SQL On Pandas最佳实践 1、PandaSQL1.1、PandaSQL简介1.2、Pandas与PandaSQL解决方案对比1.3、PandaSQL支持的窗口函数1.4、PandaSQL综合使用案例2、DuckDB2.1、DuckDB简介2.2、SQL操作（SQL On Pandas）2.3、逻辑SQL（DSL on Pandas）2.4、DuckDB on Apache Arrow2.5、DuckDB …...

编程日记 2023/10/26 13:51:30

如何批量给视频添加logo水印？

如果你想为自己的视频添加图片水印，以增强视频的辨识度和个性化，那么你可以使用固乔剪辑助手软件来实现这一需求。下面就是详细的操作步骤： 1.下载并打开固乔剪辑助手软件，这是一款简单易用的视频剪辑软件，功能丰富&am…...

编程日记 2023/10/26 13:49:28

数据挖掘和大数据的区别

数据挖掘 一般用于对企业内部系统的数据库进行筛选、整合和分析。 操作对象是数据仓库，数据相对有规律，数据量较少。 大数据 一般指对互联网中杂乱无章的数据进行筛选、整合和分析。 操作对象一般是互联网的数据，数据无规律，…...

编程日记 2023/10/26 13:48:25

Go之流程控制大全: 细节、示例与最佳实践

引言 在计算机编程中，流程控制是核心的组成部分，它决定了程序应该如何根据给定的情况执行或决策。以下是Go语言所支持的流程控制结构的简要概览： 流程控制类型代码if-else条件分支if condition { } else { }for循环for initialization; con…...

编程日记 2023/10/26 13:47:24

FLStudio2024最新破解版注册机

水果音乐制作软件FLStudio是一款功能强大的音乐创作软件,全名:Fruity Loops Studio。水果音乐制作软件FLStudio内含教程、软件、素材,是一个完整的软件音乐制作环境或数字音频工作站... FL Studio21简称FL 21，全称 Fruity Loops Studio 21，因此国人习惯叫…...

编程日记 2023/10/26 13:46:20

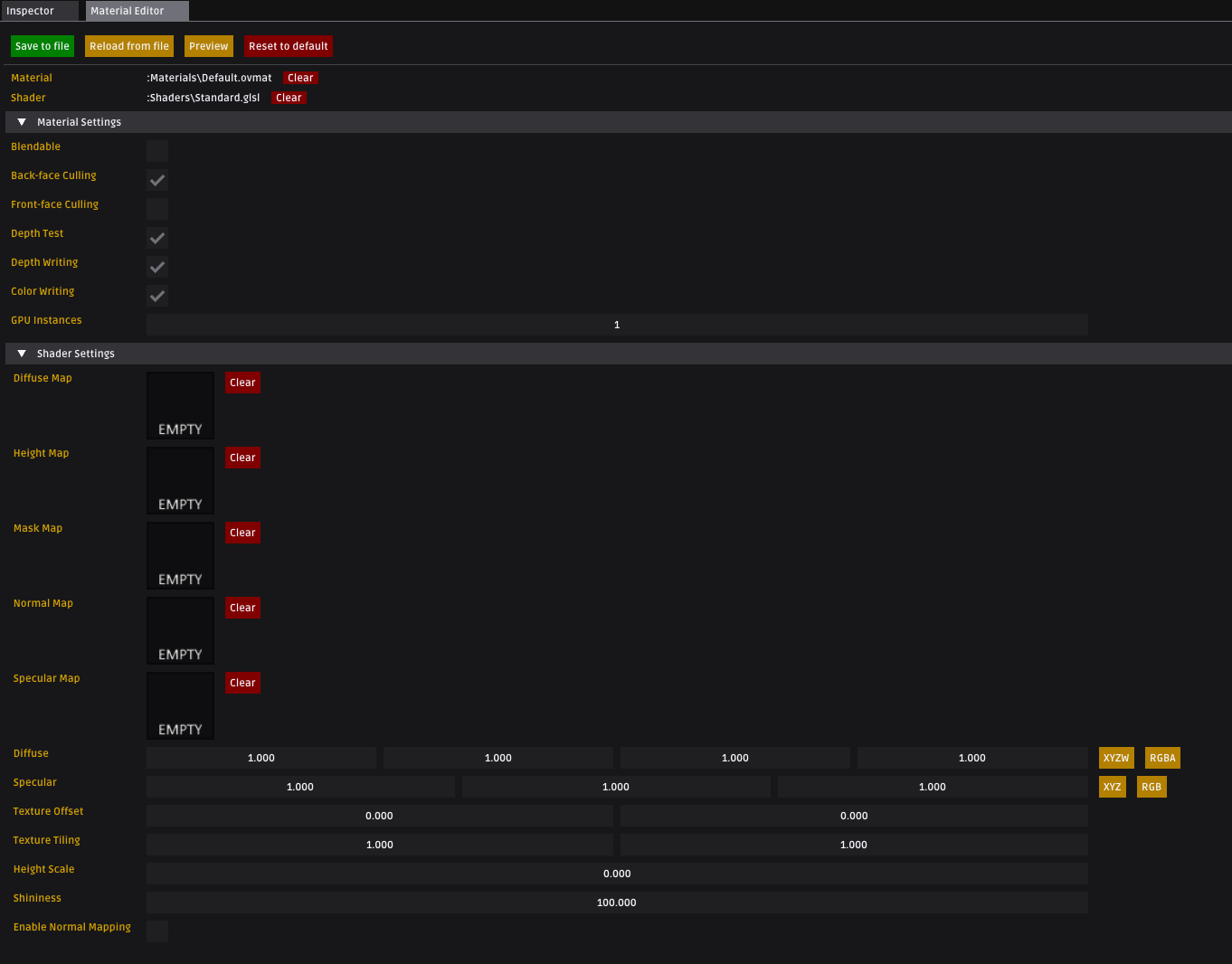
【Overload游戏引擎细节分析】standard材质Shader

提示：Shader属于GPU编程，难写难调试，阅读本文需有一定的OpenGL基础，可以写简单的Shader，不适合不会OpenGL的朋友 一、Blinn-Phong光照模型 Blinn-Phong光照模型，又称为Blinn-phong反射模型（Bli…...

编程日记 2023/10/26 13:45:19

Leetcode—7.整数反转【中等】

2023每日刷题&#xff08;十&#xff09; Leetcode—7.整数反转 关于为什么要设long变量 参考自这篇博客 long可以表示-2147483648而且只占4个字节&#xff0c;所以能满足题目要求 复杂逻辑版实现代码 int reverse(int x){int arr[32] {0};long y;int flag 1;if(x <…...

编程日记 2023/10/26 13:44:18

lua-web-utils和proxy设置示例

以下是一个使用lua-web-utils和proxy的下载器程序&#xff1a; -- 首先安装lua-web-utils库 local lwu require "lwu" ​ -- 获取服务器 local function get_proxy()local proxy_url "duoipget_proxy"local resp, code, headers, err lwu.fetch(proxy_…...

编程日记 2023/10/26 13:43:17

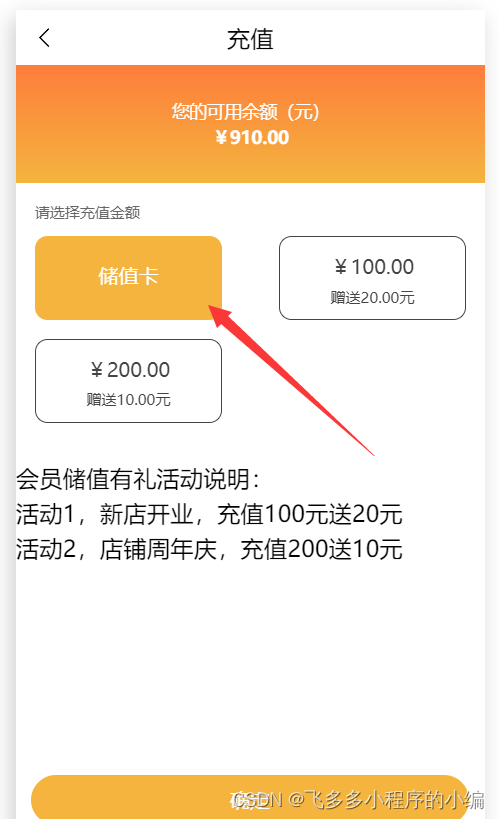
分享一下在微信小程序里怎么添加储值卡功能

在微信小程序中添加储值卡功能&#xff0c;可以让消费者更加便捷地管理和使用储值卡&#xff0c;同时也能增加商家的销售收入。下面是一篇关于如何在微信小程序中添加储值卡功能的软文。 标题&#xff1a;微信小程序添加储值卡功能&#xff0c;便捷与高效并存 随着科技的不断发…...

编程日记 2023/10/26 13:42:16

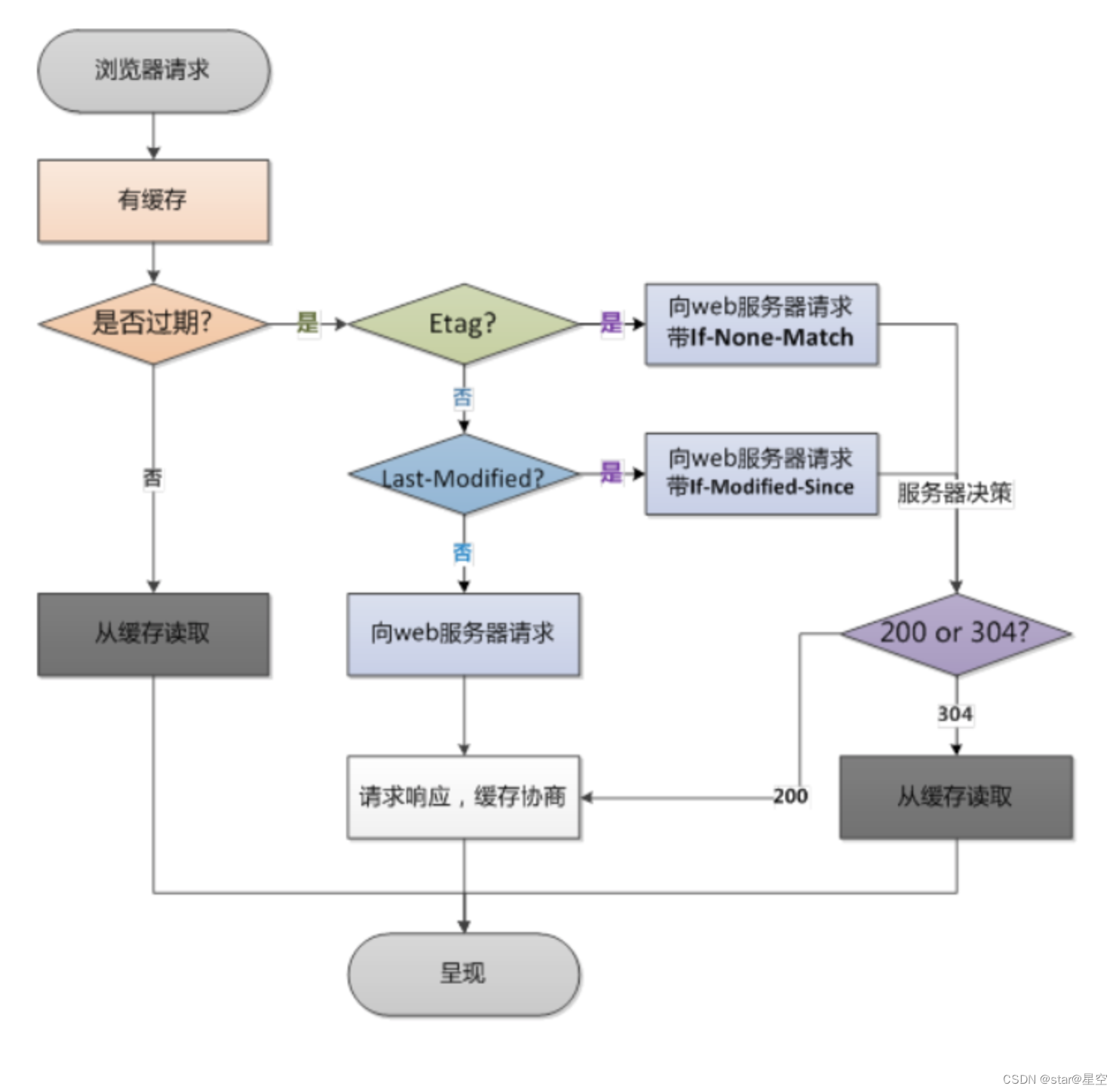
2023高频前端面试题-http

1. HTTP有哪些⽅法&#xff1f; HTTP 1.0 标准中&#xff0c;定义了3种请求⽅法&#xff1a;GET、POST、HEAD HTTP 1.1 标准中&#xff0c;新增了请求⽅法&#xff1a;PUT、PATCH、DELETE、OPTIONS、TRACE、CONNECT 2. 各个HTTP方法的具体作用是什么&#xff1f; 方法功能G…...

编程日记 2023/10/26 13:41:15

图像识别在自动驾驶汽车中的多传感器融合技术

摘要&#xff1a; 介绍文章的主要观点和发现。 引言&#xff1a; 自动驾驶汽车的兴起和重要性。多传感器融合技术在自动驾驶中的关键作用。 第一部分&#xff1a;图像识别技术 图像识别的基本原理。图像传感器和摄像头在自动驾驶中的应用。深度学习和卷积神经网络&#xff…...

编程日记 2023/10/26 13:39:13

Kafka To HBase To Hive

目录 1.在HBase中创建表 2.写入API 2.1普通模式写入hbase&#xff08;逐条写入&#xff09; 2.2普通模式写入hbase&#xff08;buffer写入&#xff09; 2.3设计模式写入hbase&#xff08;buffer写入&#xff09; 3.HBase表映射至Hive中 1.在HBase中创建表 hbase(main):00…...

编程日记 2023/10/26 13:38:12

python pandas.DataFrame 直接写入Clickhouse

import pandas as pd import sqlalchemy from clickhouse_sqlalchemy import Table, engines from sqlalchemy import create_engine, MetaData, Column import urllib.parsehost 1.1.1.1 user default password default db test port 8123 # http连接端口 engine create…...

编程日记 2023/10/26 13:37:11

德语中第二虚拟式在主动态的形式，柯桥哪里可以学德语

德语中第二虚拟式在主动态的形式 1. 对于大多数的动词&#xff0c;一般使用这样的一般现在时时态&#xff1a; wrde 动词原形 例句&#xff1a;Wenn es nicht so viel kosten wrde, wrde ich mir ein Haus am Meer kaufen. 如果不花这么多钱&#xff0c;我会在海边买一栋房…...

编程日记 2023/10/26 13:36:10

[Python进阶] 消息框、弹窗：tkinter库

6.16 消息框、弹窗&#xff1a;tkinter 6.16.1 前言 应用程序中的提示信息处理程序是非常重要的部分&#xff0c;用户要知道他输入的资料到底正不正确&#xff0c;或者是应用程序有一些提示信息要告诉用户&#xff0c;都必须通过提示信息处理程序来显示适当的信息&#xff0c…...

编程日记 2023/10/26 13:34:09

浅谈 React Hooks

React Hooks 是 React 16.8 引入的一组 API&#xff0c;用于在函数组件中使用 state 和其他 React 特性&#xff08;例如生命周期方法、context 等&#xff09;。Hooks 通过简洁的函数接口&#xff0c;解决了状态与 UI 的高度解耦&#xff0c;通过函数式编程范式实现更灵活 Rea…...

编程新知 2025/9/23 15:13:40

深度学习在微纳光子学中的应用

深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向&#xff1a; 逆向设计 通过神经网络快速预测微纳结构的光学响应&#xff0c;替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

编程新知 2026/2/8 15:03:04

CMake基础：构建流程详解

目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

编程新知 2026/2/2 7:39:34

现代密码学 | 椭圆曲线密码学—附py代码

Elliptic Curve Cryptography 椭圆曲线密码学&#xff08;ECC&#xff09;是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础&#xff0c;例如椭圆曲线数字签…...

编程新知 2026/2/6 7:30:33

爬虫基础学习day2

# 爬虫设计领域 工商&#xff1a;企查查、天眼查短视频&#xff1a;抖音、快手、西瓜 ---> 飞瓜电商&#xff1a;京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空&#xff1a;抓取所有航空公司价格 ---> 去哪儿自媒体&#xff1a;采集自媒体数据进…...

编程新知 2025/12/5 3:38:11

精益数据分析（97/126）：邮件营销与用户参与度的关键指标优化指南

精益数据分析&#xff08;97/126&#xff09;&#xff1a;邮件营销与用户参与度的关键指标优化指南 在数字化营销时代&#xff0c;邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天&#xff0c;我们将深入解析邮件打开率、网站可用性、页面参与时…...

编程新知 2025/12/13 4:04:33

Fabric V2.5 通用溯源系统——增加图片上传与下载功能

fabric-trace项目在发布一年后，部署量已突破1000次，为支持更多场景，现新增支持图片信息上链，本文对图片上传、下载功能代码进行梳理，包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源，需要对底层数据结构进行修改，在此对智能合约中的农产品数…...

编程新知 2025/9/27 12:03:43

R 语言科研绘图第 55 期 --- 网络图-聚类

在发表科研论文的过程中&#xff0c;科研绘图是必不可少的&#xff0c;一张好看的图形会是文章很大的加分项。 为了便于使用&#xff0c;本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中&#xff0c;获取方式&#xff1a; R 语言科研绘图模板 --- sciRplothttps://mp.…...

编程新知 2026/1/30 2:34:31

Caliper 配置文件解析：fisco-bcos.json

config.yaml 文件 config.yaml 是 Caliper 的主配置文件，通常包含以下内容： test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

编程新知 2025/10/24 15:14:02

离线语音识别方案分析

随着人工智能技术的不断发展&#xff0c;语音识别技术也得到了广泛的应用&#xff0c;从智能家居到车载系统&#xff0c;语音识别正在改变我们与设备的交互方式。尤其是离线语音识别&#xff0c;由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力&#xff0c;广…...

编程新知 2025/9/22 13:00:25