C++数据结构X篇_21_插入排序(稳定的排序)
文章目录
- 1. 插入排序原理
- 2. 算法图解
- 3. 核心代码:
- 4. 插入排序整体代码实现
1. 插入排序原理
插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
- 原理是将无序序列插入到有序序列中
- 直接插入排序的两种性质:
-
当待排序的原序列中大多数元素都已有序的情况下,此时进行的元素比较和移动的次数较少;
-
当原序列的长度很小时,即便它的所有元素都是无序的,此时进行的元素比较和移动的次数还是很少。
后篇介绍的希尔排序就是基于上面2个性质的改进
2. 算法图解
将待排序的集合看做两部分,已排序的区间(0…i) ; 待排序的区间[i…n);每次选择无序区间的第一个元素插入到有序区间的合适位置,直到整个数组有序。
因为不知道数组中得前几个元素是已经有序的,所以直接从第二个元素开始执行插入排序,将每个元素都进行一次插入排序。
算法图解如下:

3. 核心代码:
void insert_sort(int arr[], int length) //升序
{int j;//第一个元素当做有序的,第二个看做无序,从第二个插入第一个元素并进行比较for (int i = 1; i < length; i++){if (arr[i] < arr[i - 1]) //比升序序列最大值要小,进入插入排序{int temp = arr[i];//从右向左for (j = i - 1; j >= 0; j--){if (temp < arr[j]) //升序序列中元素大于arr[i]{arr[j + 1] = arr[j]; //向前移动一位}else{break;}}arr[j + 1] = temp;}}
}
4. 插入排序整体代码实现
#include <iostream>
using namespace std;void swap(int* a, int* b)
{int temp = *a;*a = *b;*b = temp;
}//打印数组
void printArr(int arr[])
{for (int i = 0; i < 10; i++){cout << arr[i] << endl;}
}//插入排序
void insert_sort(int arr[], int length) //升序
{int j;for (int i = 1; i < length; i++){if (arr[i] < arr[i - 1]) //比升序序列最大值要小{int temp = arr[i];for (j = i - 1; j >= 0; j--){if (temp < arr[j]) //升序序列中元素大于arr[i]{arr[j + 1] = arr[j]; //向前移动一位}else{break;}}arr[j + 1] = temp;}}printArr(arr);
}int main()
{int arr[] = { 8,2,3,9,6,4,7,1,5,10 };insert_sort(arr, 10);system("pause");return 0;
}
运行结果:
- 插入排序,插入排序代码实现,插入排序代码思路梳理
- 优秀博文:十大经典排序算法-插入排序算法详解,常见的几种排序(C++)
相关文章:

C++数据结构X篇_21_插入排序(稳定的排序)
文章目录 1. 插入排序原理2. 算法图解3. 核心代码:4. 插入排序整体代码实现 1. 插入排序原理 插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相…...
【Unity】3D跑酷游戏
展示 finish_all * 方块跑酷 1.教程链接 翻墙:https://www.youtube.com/watch?v9ZEu_I-ido4&listPLPV2KyIb3jR53Jce9hP7G5xC4O9AgnOuL&index3 2.基础制作 最终成果 2.1 基本场景 1.创建Cube作为跑道 1)记得把位置Reset; 2&#…...
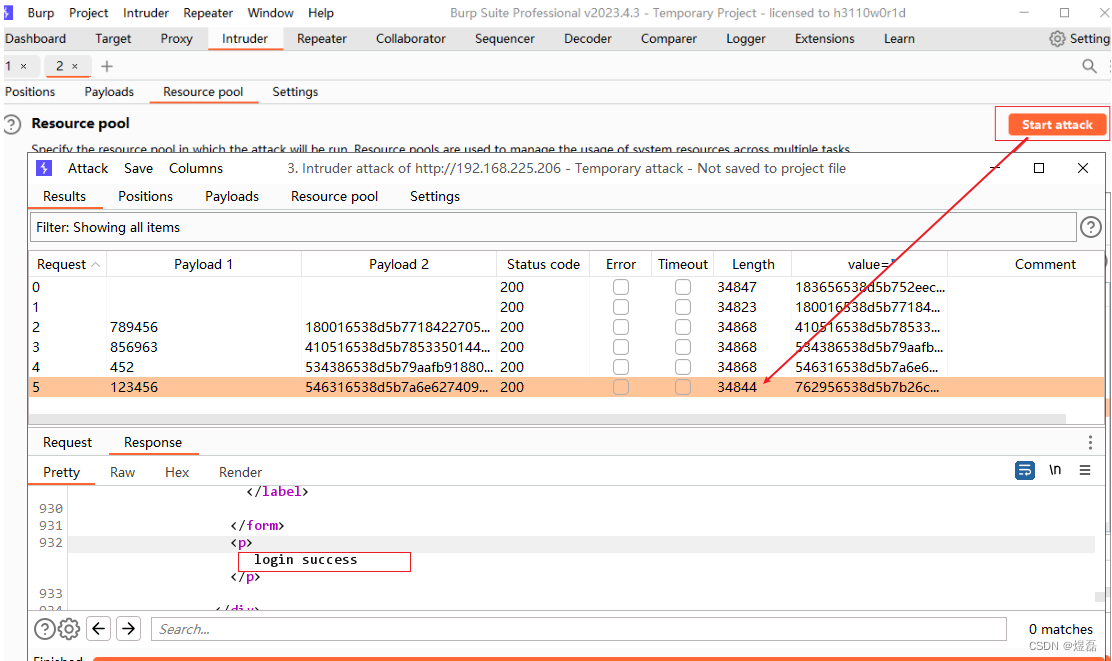
bp前端验证码绕过及token绕过
前端验证码绕过及token绕过 原文参考:xiu 文章目录 前端验证码绕过及token绕过原文参考:[xiu](http://www.xiusafe.com/2023/10/25/%E9%AA%8C%E8%AF%81%E7%A0%81%E7%BB%95%E8%BF%87/)1 验证码爆破1. 登录Pikachu,先获取登录的api接口2 验证码…...

Jmeter(十四):跨线程组传递jmeter变量及cookie的处理详解
setUp线程组 setUp thread group 一种特殊类型的线程组,用于在执行常规线程组之前执行一些必要的操作。 在 setup线程组下提到的线程行为与普通线程组完全相同。不同的是执行顺序--- 它会在普通线程组执行之前被触发; 应用场景举例: A、测…...
css实现圆形进度条
能用现成组件就用,实现不行再自己写,因为牵扯到上传文件,进度实时出不来,所以只能使用dom元素操作; 1.实现 效果: 上图是100%,如果需要根据百分比显示,我们需要看下代码里面left和…...

适用于 Windows 10 和 Windows 11 设备的笔记本电脑管理软件
便携式计算机管理软件使 IT 管理员能够简化企业中使用的便携式计算机的部署和管理,当今大多数员工使用Windows 笔记本电脑作为他们的主要工作机器,他们确实已成为几乎每个组织不可或缺的一部分。由于与台式机相比,笔记本电脑足够便携…...

YOLOv5论文作图教程(1)— 软件介绍及下载安装(包括软件包+下载安装详细步骤)
前言:Hello大家好,我是小哥谈。在学习YOLOv5算法的过程中,很多同学都有发表论文的需求。作为文章内容的支撑,图表是最直接的整合数据的工具,能够更清晰地反映出研究对象的结果、流程或趋势。在发表论文的时候,审稿人除了关注论文的内容和排版外,也会审核图表是否清晰美观…...
AutoCAD 2024 Mac中文附激活补丁 兼容M1.M2电脑
AutoCAD 2024是一款功能强大的CAD设计绘图工具,旨在帮助用户创建和编辑高质量的设计图纸和模型。该软件支持2D和3D设计,具有丰富的功能和工具,可用于绘图、建模、注释、标注、尺寸设置等多种操作。AutoCAD 2024还引入了智能对象捕捉、实时预览…...

Jmeter基础---while控制器举例说明
一、 While 控制器 首先创建一个While Controller (While 循环控制器) 设置界面如下: Condition (function or variable) :条件说明 条件为 Flase 的时候,才会跳出 While 循环,否则一直执行 While 控制器下的样例 1、不填…...
正点原子嵌入式linux驱动开发——RGB转HDMI
目前大多数的显示器都提供了HDMI接口,HDMI的应用范围也越来越广,但是STM32MP157这颗芯片原生并不支持HDMI显示。可以通过RGB转HDMI芯片将RGB信号转为HDMI信号,这样就可以连接HDMI显示器了。本章就来学习一下如何在正点原子的STM32MP1开发板上…...
前端时间分片渲染
在经典的面试题中:”如果后端返回了十万条数据要你插入到页面中,你会怎么处理?” 除了像 useVirtualList 这样的虚拟列表来处理外,我们还可以通过 时间分片 来处理 通过 setTimeout 直接上一个例子: <!--* Autho…...

亿图导出word和PDF中清晰度保留方法
步骤一 在亿图软件中画一个元件大小搭配合理的图。注意字体大小的安排,尤其是角标的大小要合适,示范如下 选中所有元器件,右键使用组合功能将电路图组合为一个整体 步骤二: 将亿图软件中的图保存为SVG格式。示范如下 在导出到…...
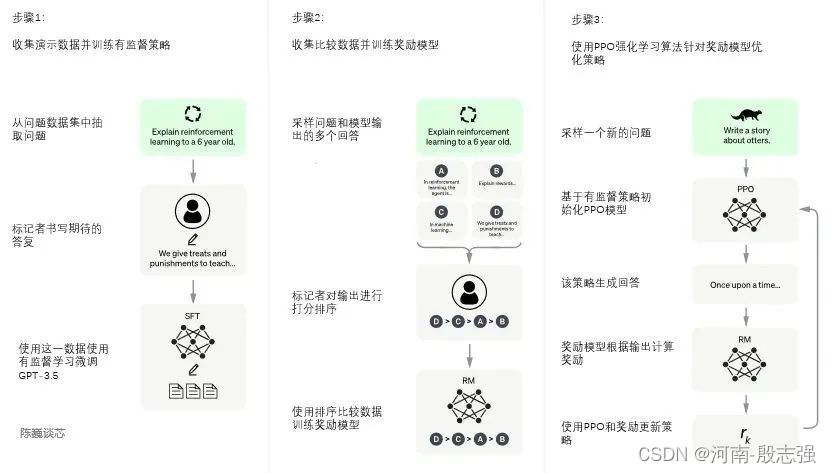
chatGPT结构及商业级相似模型应用调研
GPT前言 说明 ChatGPT这项技术的历史可以追溯到2018年,当时由Facebook实验室的团队开发出该技术,以开发聊天机器人为目的。随后,ChatGPT在2019年由来自谷歌的DeepMind团队在国际会议ICLR上发表了论文,其中提出了ChatGPT的技术框架…...

HarmonyOS鸿蒙原生应用开发设计- 华为分享图标
HarmonyOS设计文档中,为大家提供了独特的华为分享图标,开发者可以根据需要直接引用。 开发者直接使用官方提供的华为分享图标内容,既可以符合HarmonyOS原生应用的开发上架运营规范,又可以防止使用别人的内容产生的侵权意外情况等&…...

Java基础-反射
代理相关 为什么需要代理? 代理可以无侵入式的对方法进行增强,而不需要修改原始方法的代码,这样就可以在不修改原始方法的情况下,对方法进行增强。 代理长什么样子? 代理里面就是对象要被代理的方法 Java通过什么方式…...
计算机毕设 大数据二手房数据爬取与分析可视化 -python 数据分析 可视化
# 1 前言 🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升,传统的毕设题目缺少创新和亮点,往往达不到毕业答辩的要求,这两年不断有学弟学妹告诉学长自己做的项目系统达不到老师的要求。 为了大家能够顺利以及最少的精力通…...

【转载】 Bytedance火山引擎智能拥塞控制算法 VICC
BytedanceTechBlog : 火山引擎实时、低延时拥塞控制算法的优化实践 火山引擎 网站如何利用播放器节省20%点播成本点击下面的链接进入原文:原创 翟强俊、唐辉 字节跳动技术团队 2023-10-18 11:59 发表于北京 一些专利摘要 火山引擎智能拥塞控制算法 VICC(Volcano Intelligent…...
Postman如何测试WebService接口
前言: 由于工作所需,需要使用Postman测试工具,对基于ws规范的WebService接口进行测试.在经过多种尝试后,终于找到了正确的测试方法.下面我便详细记录测试步骤,以便以后再次测试时可以拿来主义. 第一步:确保WebService服务端正常启动(注意服务端各个接口发布的url地址) 第二步…...
微服务-Eureka
文章目录 提供者与消费者Eureka注册中心搭建EurekaServer服务注册服务发现项目结构 提供者与消费者 Eureka注册中心 服务消费者该如何获取服务提供者的地址信息? 服务提供者启动时向eureka注册自己的信息 eureka保存这些信息 消费者根据服务名称向eureka拉取提供者信…...

超声电机工作原理
超声波电机的工作原理 在压电陶瓷振子上加高频交流电压时,利用逆压电效应或电致伸缩效应使定子产生微观机械振动。并将这种振动通过共振放大和摩擦耦合变换成旋转或直线型运动。 超声波驱动有两个前提条件: 需在定子表面激励出稳态的质点椭圆运动轨迹…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
