西北工业大学大学物理(II)期末试题选填解析2021-2022


2 金属薄片,就暗示了载流子是电子了。
3 熟练掌握左右手即可。
4 又是位移电流。
6 感应电场。随时间变化着的磁场能在其周围空间激发一种电场,它能对处于其中的带电粒子施以力的作用,这就是涡旋电场,又叫感生电场。涡旋电场是非保守场,它的电场线是闭合曲线,这一点不同于静电场,涡旋电场力是导致感应电动势的非静电力。

7 结合图中的两个公式即可。另外直观理解也不是不可以。
8 考查的是德布罗意关系。记住那两个式子。E和p
9 微观粒子满足不确定性关系是因为波粒二象性。
10 几率变得话总的就超过1了,根本不可能。
填空:
1 圆面无磁感线通过。
2 高中公式。
3 第二次见到考自感。
5 一定区间上的分子平均速率公式。

6 这个题,其实只需要k,NA可以消掉,R可以转化。具体关系要记好。

7 不考虑相对论效应,m不变。
8 λ^2/Δλ,书上推出来了,也不难推导。
9 ms两种可能,ml是(2l+1)种,不要忘了0
10 平方带入即可。
相关文章:

西北工业大学大学物理(II)期末试题选填解析2021-2022
2 金属薄片,就暗示了载流子是电子了。3 熟练掌握左右手即可。4 又是位移电流。6 感应电场。随时间变化着的磁场能在其周围空间激发一种电场,它能对处于其中的带电粒子施以力的作用,这就是涡旋电场,又叫感生电场。涡旋电场是非保守…...
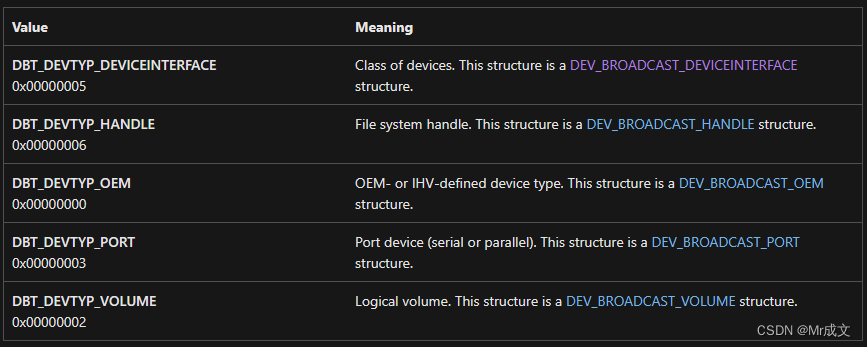
【USB】windows热插拔通知接口分析
文章目录接口介绍概述过滤器介绍举例接收通知创建窗口参考文档接口介绍 概述 window提供了RegisterDeviceNotificationW方法,可以用来监听设备的热插拔事件。 HDEVNOTIFY RegisterDeviceNotificationW([in] HANDLE hRecipient,[in] LPVOID NotificationFilter,[in]…...

CMake入门
课程地址 文档地址 CMake可以用于所有的编程语言 HelloWorld 编写一个C文件: //hello.cpp #include <iostream>int main() {std::cout << "hello, world" <<std::endl;return 0; }手动编译: c hello.cpp书写CMakeList…...

python中一种编写config文件并及时更新的方法
contents0. Intro1. config.py2. 调用以及更新0. Intro 在pytorch或者其他深度学习框架中,有许多超参数需要调整,包括learning_rate,training_data_path等,因此编写一个config文件统一存放这些参数,方便调用/查看/修改…...
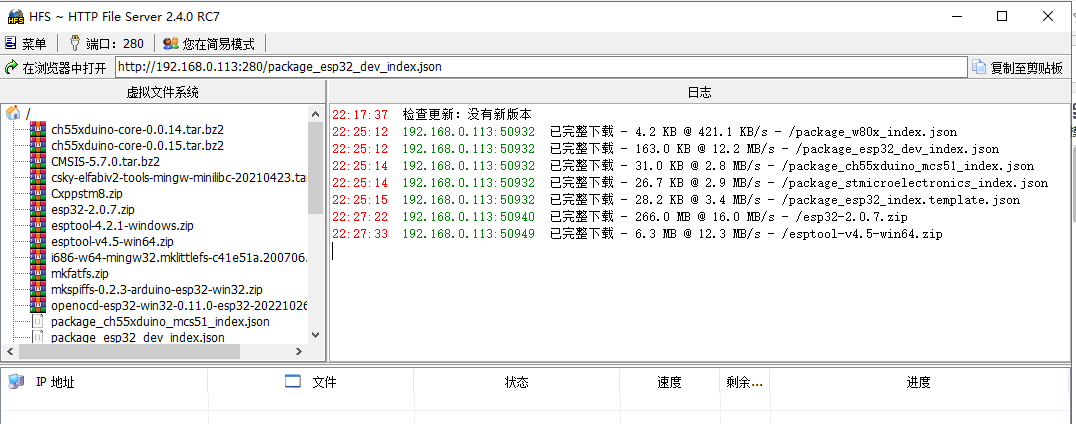
基于Windows下离线安装当前最新Arduino ESP32 SDK(2.0.7)固件开发包
基于Windows下离线安装当前最新Arduino ESP32 SDK(2.0.7)固件开发包✨写这篇的文章的初衷,是由于在前几天想通过离线一键安装包方式实现升级安装,结果发现解压后,可以找到开发板,但是无法上传代码ÿ…...
)
Android 9.0 app添加校验锁(输入密码才能进入app)
1.概述 在9.0的系统rom定制化开发中,在一些产品开发中,需要对app启动校验密码,输入密码后,才可以进app,所以说对这种 开发需求,首先找到启动app的关键点以后,在加入限制app启动的弹窗,输入密码,密码正确后在进入app,实现流程 就是这样,接下来看如何实现的 2.app添加校…...

注意力机制详解系列(二):通道注意力机制
👨💻作者简介: 大数据专业硕士在读,CSDN人工智能领域博客专家,阿里云专家博主,专注大数据与人工智能知识分享。 🎉专栏推荐: 目前在写CV方向专栏,更新不限于目标检测、…...

动态规划-规划兼职工作
动态规划-规划兼职工作 一、问题描述 你打算利用空闲时间来做兼职工作赚些零花钱。这里有 n 份兼职工作,每份工作预计从 startTime 开始到 endTime 结束,报酬为 profit。给你一份兼职工作表,包含开始时间 startTime,结束时间 en…...

Redis学习笔记(二)Redis基础(基于5.0.5版本)
一、Redis定位与特性 Redis是一个速度非常快的非关系数据库(non-relational database),用 Key-Value 的形式来存储数据。数据主要存储在内存中,所以Redis的速度非常快,另外Redis也可以将内存中的数据持久化到硬盘上。…...

Ancaonda常用cmd命令总结
1) 查看以创建的虚拟环境: conda info --envs / conda env list 2) 激活创建的环境:conda activate xxx(虚拟环境名称) 3) 退出激活的环境:conda deactivate 4) 删除一个已有虚拟环境:conda remove --name(已创建虚拟…...

yolov5_reid【附代码,行人重识别,可做跨视频人员检测】
该项目利用yolov5reid实现的行人重识别功能,可做跨视频人员检测。 应用场景: 可根据行人的穿着、体貌等特征在视频中进行检索,可以把这个人在各个不同摄像头出现时检测出来。可应用于犯罪嫌疑人检索、寻找走失儿童等。 支持功能:…...
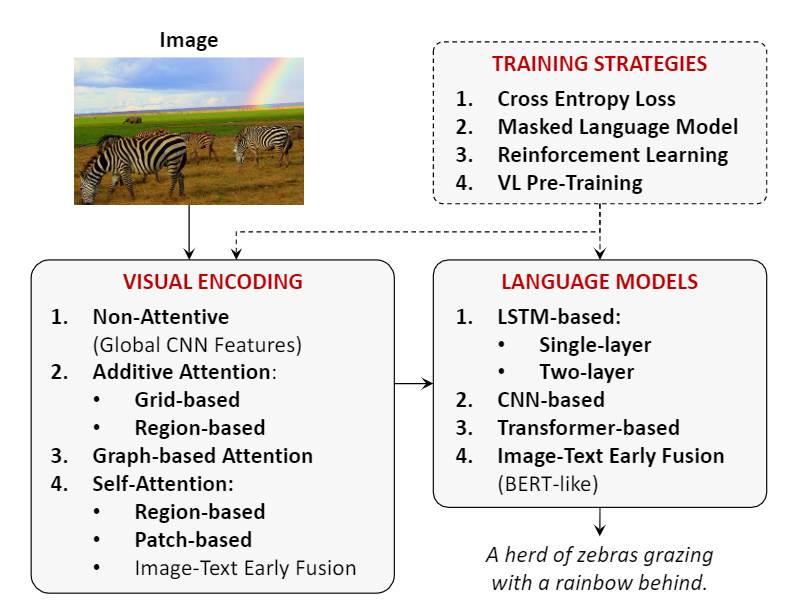
多模态预训练模型综述
经典预训练模型还未完成后续补上预训练模型在NLP和CV上取得巨大成功,学术届借鉴预训练模型>下游任务finetune>prompt训练>人机指令alignment这套模式,利用多模态数据集训练一个大的多模态预训练模型(跨模态信息表示)来解…...

华为OD机试题,用 Java 解【玩牌高手】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...
数学建模 latex 图片以及表格排版整理(overleaf)
无论是什么比赛,图片和表格的格式都非常重要,这边的重要不只是指规范性,还有抓住评委眼球的能力。 那么怎样抓住评委的眼球? 最重要的一点就是善用图片和表格(当然撰写论文最重要的是逻辑,这个是需要长期…...
进程优先级(Linux)
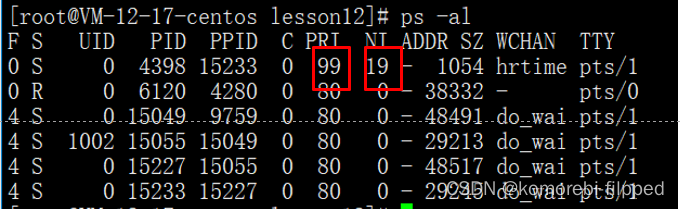
目录 优先级VS权限 基本概念 查看系统进程 几个重要信息 PRI and NI PRI vs NI top命令 上限: 详细步骤 下限: 其他概念 优先级VS权限 权限:能or不能 优先级:已经能,但是谁先谁后的问题(CPU资源有…...
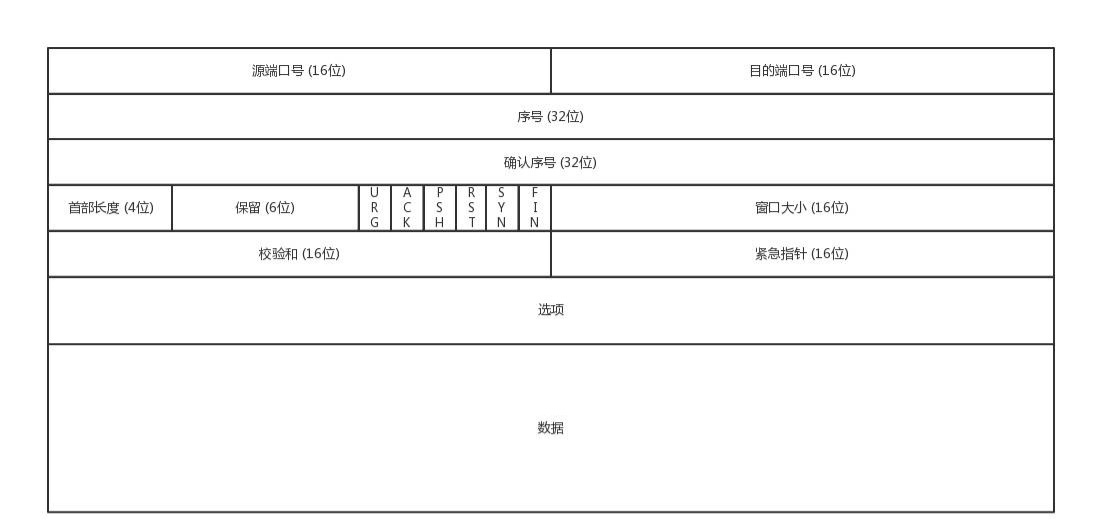
[面试直通版]网络协议面试核心之IP,TCP,UDP-TCP与UDP协议的区别
点击->计算机网络复习的文章集<-点击 目录 前言 UDP TCP 区别小总结 前言 TCP和UDP都是在传输层,在程序之间传输数据传输层OSI模型:第四层TCP/IP模型:第三层关键协议:TCP协议、UDP协议传输层属于主机间不同进程的通信传…...
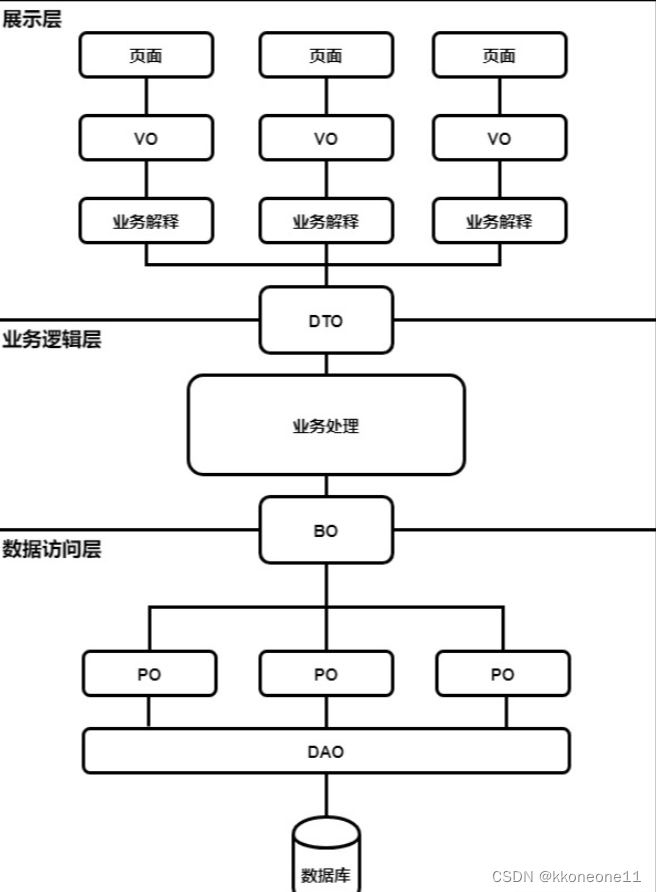
VO,BO,PO,DO,DTO,AO的区别
DTO(Data Transfer Object)数据传输对象 这个传输通常指的前后端之间的传输 1.在前端的时候: 存在形式通常是js里面的对象(也可以简单理解成json),也就是通过ajax请求的那个数据体 2.在后端的时候&…...

JavaSE学习笔记day15
零、 复习昨日 HashSet 不允许重复元素,无序 HashSet去重原理: 先比较hashcode,如果hashcode不一致,直接存储如果hashcode值一样,再比较equals如果equals值为true,则认为完全一样,不存储即去重否则存储 如果使用的是空参构造创建出的TreeSet集合,那么它底层使用的就是自然排序,…...
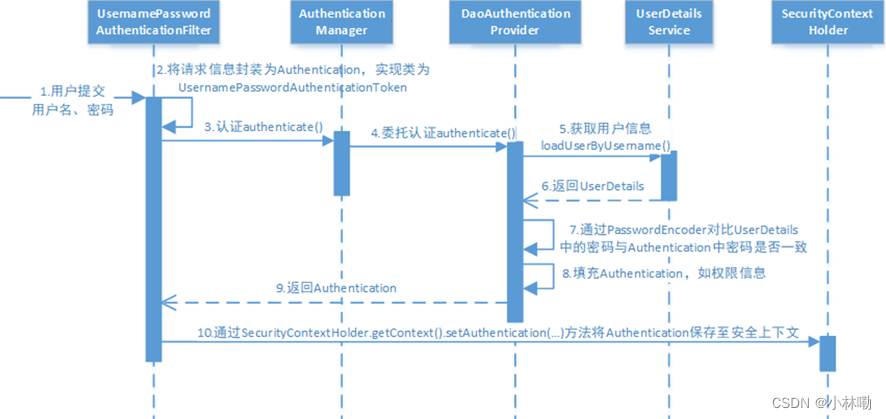
Spring Security认证研究
1.项目中认证的三种方式: 1.统一认证 认证通过由认证服务向给用户颁发令牌,相当于访问系统的通行证,用户拿着令牌去访问系统的资源。 2.单点登录,对于微服务项目,因为包含多个模块,所以单点登录就是使得用户…...

BigKey、布隆过滤器、分布式锁、红锁
文章目录 BigKey发现 BigKey如何删除BigKeyunlinkdelBigKey配置优化布隆过滤器布隆过滤器构建、使用、减少误判布隆过滤器二进制数组,如何处理删除?实现白名单 whitelistCustomer解决缓存穿透分布式锁依赖Redis 分布式锁代码使用红锁POM依赖yaml使用其他redis分布式锁容错率公…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
