使用Python进行数据分析——线性回归分析
大家好,线性回归是确定两种或两种以上变量之间互相依赖的定量关系的一种统计分析方法。根据自变量的个数,可以将线性回归分为一元线性回归和多元线性回归分析。
一元线性回归:就是只包含一个自变量,且该自变量与因变量之间的关系是线性关系。例如通过广告费这一个自变量来预测销量,就属于一元线性回归分析。
多元线性回归:如果回归分析包含两个或以上的自变量,且每个因变量与自变量之间都是线性关系,,则成为多元线性回归分析;例如通过肥料、灌溉等人工成本来预测产量,就属于多元线性回归。
一、线性回归分析的思路
确定因变量与自变量。比如通过人工成本费进行产量预测时,人工成本费是自变量,产量是因变量。
确定线性回归分析的类型。例如在一元线性回归分析中,只需要确定自变量与因变量的相关度为强相关性,即可建立一元线性回归方程,从而确定线性回归分析的类型为一元线性回归。
建立线性回归分析模型。
检验线性回归分析模型的拟合程度。为了判断线性回归分析模型是否可用于实际检测,需要检验线性回归分析模型的拟合程度,也就是对模型进行评估,主要以这三个值作为评估标准:(R-squared统计学中的)、Adj.R-squared(即Adiustd )、P值;其中前两个用来衡量线性拟合的拟合程度,P值用来衡量特征变量的显著性。
利用线性回归分析模型进行预测。如果拟合出来的回归分析模型的拟合度符合要求,就可以使用该模型以及计算出的系数a和b得到回归方程,从而根据已有的自变量数据来预测需要的因变量结果。
二、一元线性回归分析
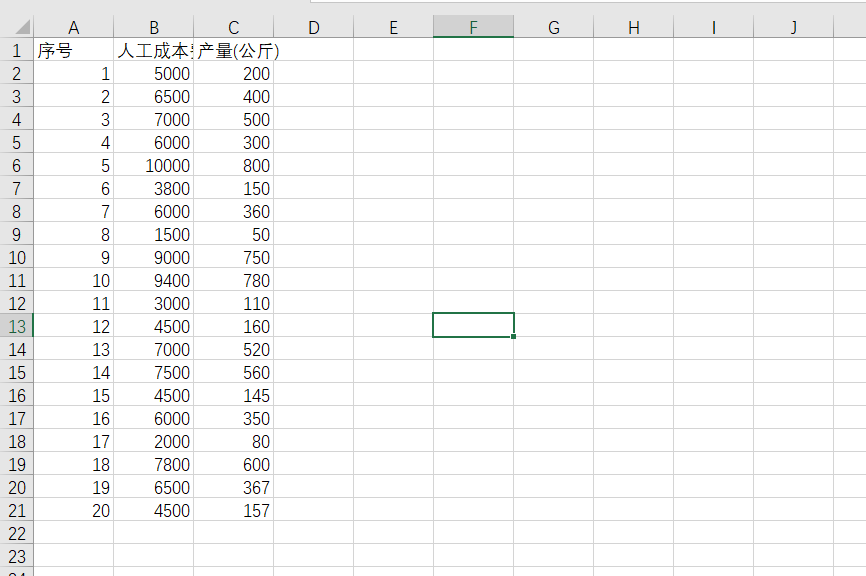
那我们初中学过的一元一次方程y=ax+b来说:就是最简单的一元线性回归,接下来,我们以上图数据为例,假设当人工成本为6600元时,产量为多少?我们下面就这一实际生产问题问题进行一元线性回归分析代码演示。
确定因变量与自变量:
import pandas as pd
data= pd.read_excel('D:/shujufenxi/作物表型记录本.xlsx',sheet_name=0,index_col='序号')
print(data.head())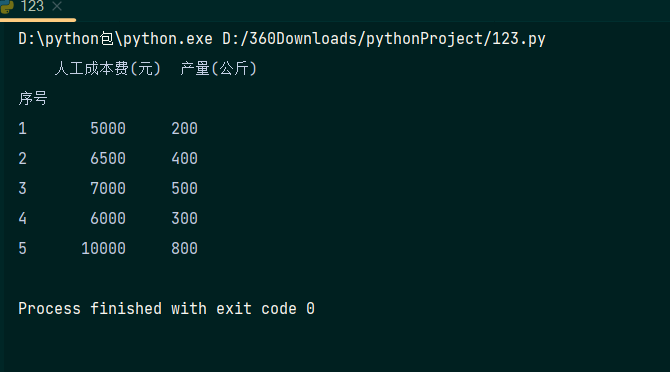
我们要进行的是根据已知的6600人工成本预测产量,由此可知,人工成本费为自变量,产量为因变量。
确定线性回归分析的类型:
import pandas as pd
data= pd.read_excel('D:/shujufenxi/作物表型记录本.xlsx',sheet_name=0,index_col='序号')
print(data.head())
# 选中自变量与因变量的数据,x为自变量,y为因变量
x=data[['人工成本费(元)']]
y=data[['产量(公斤)']]
# 确定线性回归分析的类型
corr=data.corr()
print(corr)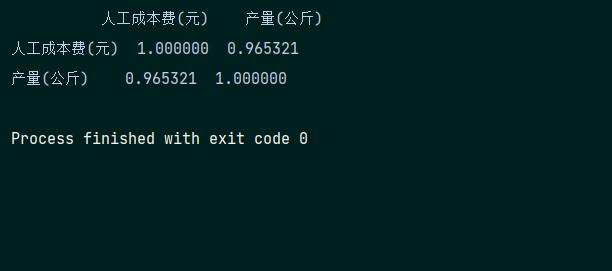
可以看到人工成本与产量之间的相关系数为0.965321,为强相关,随后利用Matplotlib模块进行绘制散点图,代码如下:
# 绘制散点图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.scatter(x,y)
plt.xlabel('人工成本费(元)')
plt.ylabel('产量(公斤)')
plt.show()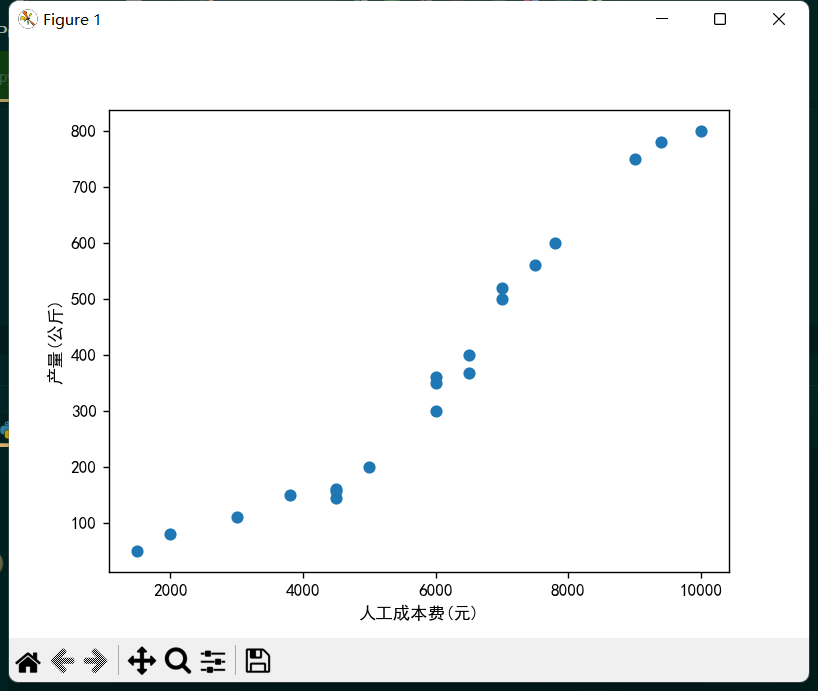
建立回归分析模型以及检验线性回归分析模型的拟合程度:
#建立回归分析模型
from sklearn.linear_model import LinearRegression # 需下载Scikit-Learn模块,使用LinearRegression()函数建立线性回归分析模型
Model=LinearRegression()
Model.fit(x,y)
#检验线性回归分析模型的拟合程度
score=Model.score(x,y)
print(score)
plt.scatter(x,y)
plt.plot(x,Model.predict(x))
plt.xlabel('人工成本费(元)')
plt.ylabel('产量(公斤)')
plt.show()
可以看出模型的评分约为0.93,很接近1,拟合程度还是较高的。
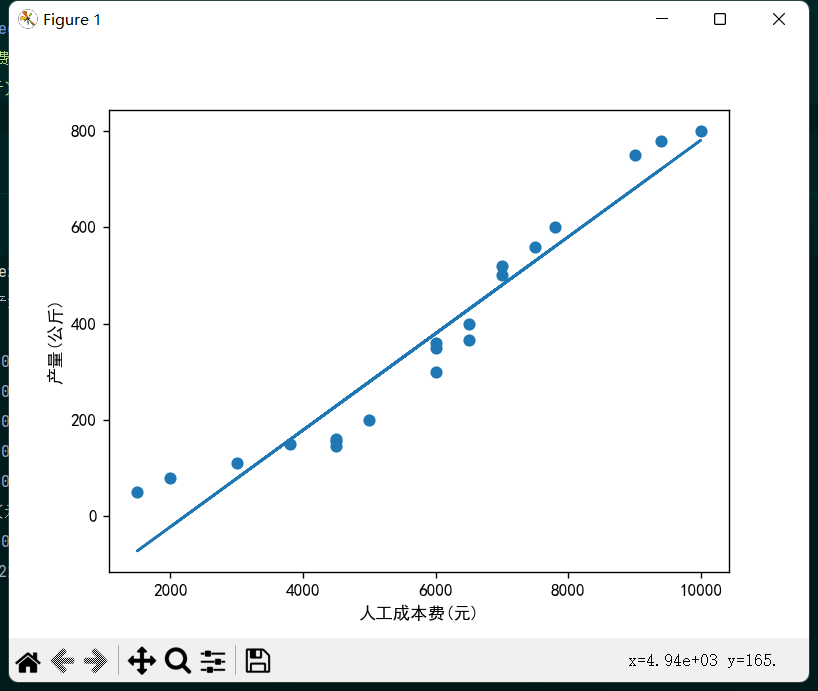
可以看出大多数散点还是比较靠近这条直线的,说明模型很好的捕捉到了数据特征,可以算是恰当拟合。
利用线性回归分析进行预测:
# 预测,也可以进行同时预测多个,如下
y=Model.predict([[6600],[15000],[8888]])
print(y)
三、多元线性回归分析
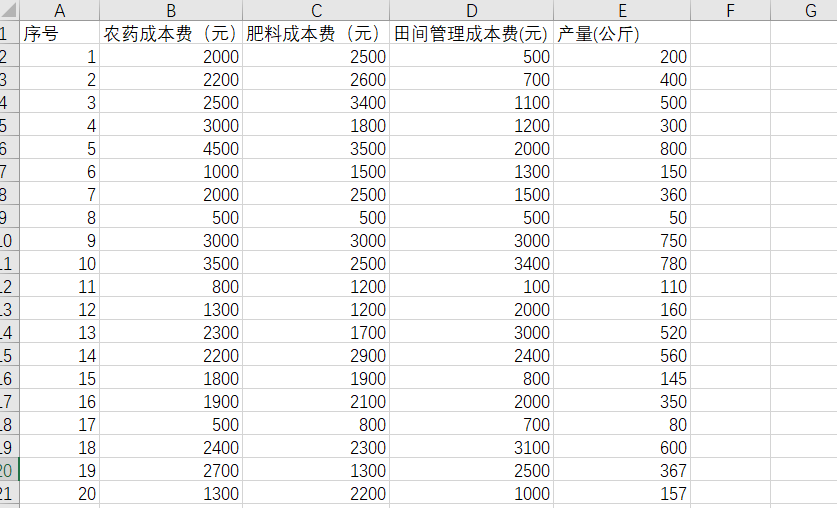
下面我们利用此虚拟数据假设当农药成本费、肥料成本费、田间管理成本费分别为3400、2900、3100时的产量为多少,下面我们将进行完整代码演示:
## 确定自变量与因变量
import pandas as pd
data= pd.read_excel('D:/shujufenxi/作物表型记录本.xlsx',sheet_name=1,index_col='序号')
print(data.head())
# 选中自变量与因变量的数据,x为自变量,y为因变量
x=data[['农药成本费(元)','肥料成本费(元)','田间管理成本费(元)']]
y=data[['产量(公斤)']]
# 确定线性回归分析的类型——图3
corr=data.corr()
print(corr)
# 绘制散点图——图1
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
sns.pairplot(data,x_vars=['农药成本费(元)','肥料成本费(元)','田间管理成本费(元)'],y_vars='产量(公斤)')
plt.show()#建立回归分析模型
from sklearn.linear_model import LinearRegression # 需下载Scikit-Learn模块,使用LinearRegression()函数建立线性回归分析模型
Model=LinearRegression()
Model.fit(x,y)
#检验线性回归分析模型的拟合程度——图3
score=Model.score(x,y)
print(score)
# 绘制拟合成果图——图2
sns.pairplot(data,x_vars=['农药成本费(元)','肥料成本费(元)','田间管理成本费(元)'],y_vars='产量(公斤)',kind='reg')# kind参数可添加一条最佳拟合直线和95%的置信带,从而更直观的展示模型的拟合程度
plt.show()# 预测,也可以进行同时预测多个,如下——图3
y=Model.predict([[3400,2900,3100]])
print(y)
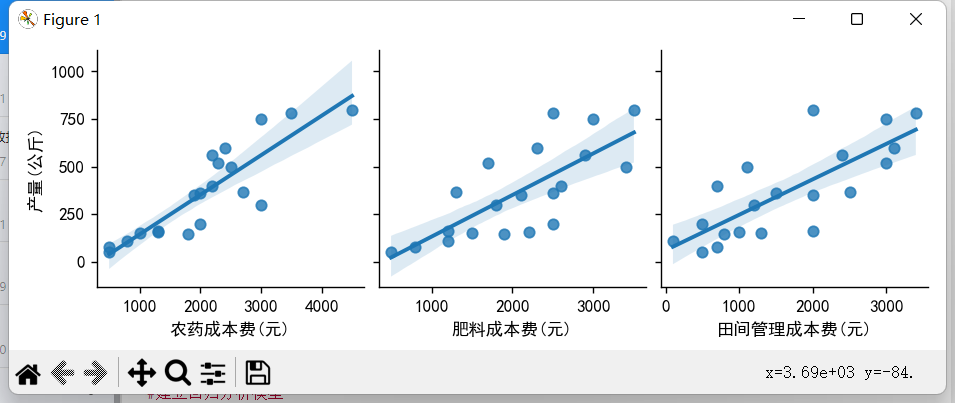
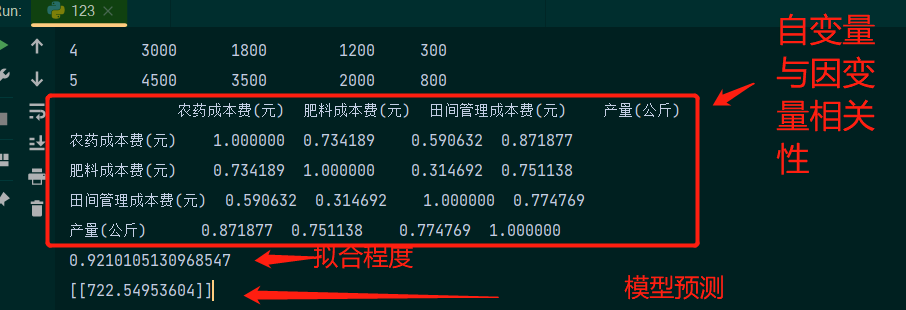
以上就是根据此数据所进行的多元线性回归分析以及模型预测;在上面第二个图中,我们从置信带的宽度来看,农药成本费与产量的线性关系较强,肥料成本费、田间管理成本费两者与产量的线性关系则较弱。
本文所讲对模型进行拟合在实际生产中具有重大意义,不仅可以利用已知变量预测未知变量,还能根据拟合结果判断所得数据是否具有生产意义。
相关文章:

使用Python进行数据分析——线性回归分析
大家好,线性回归是确定两种或两种以上变量之间互相依赖的定量关系的一种统计分析方法。根据自变量的个数,可以将线性回归分为一元线性回归和多元线性回归分析。一元线性回归:就是只包含一个自变量,且该自变量与因变量之间的关系是…...

我眼中的柔宇科技
关注、星标公众号,直达精彩内容来源:技术让梦想更伟大作者:李肖遥很早就知道了柔宇科技,当时是因为知道创始人刘自鸿,23岁清华本硕毕业,26岁获斯坦福大学电子工程博士学位,历时不超过3年&#x…...
Allegro如何快速把视图居中显示操作指导
Allegro如何快速把视图居中显示操作指导 用Allegro进行PCB设计的时候,为了方便检查和设计,时常需要将视图居中显示。一般地,会使用鼠标的中键进行放大和缩小,或者使用Zoom in和Zoom out来调整视图 Allegro还支持快速将视图居中 具体操作如下 点击View...

搜索相关功能
一、进入搜索页面 1.1 在pages下创建搜索页面为:search 1.2 在index.vue中点击进入搜素页面 onNavigationBarButtonTap(e){if(e.floatleft){uni.navigateTo({url:/pages/search/search})}},1.3 在pages.json中配置搜索页面头部 {"path" : "pages/…...

【从零开始制作 bt 下载器】一、了解 torrent 文件
【从零开始制作 bt 下载器】一、了解 torrent 文件写作背景了解 torrent 文件认识 bencodepython 解析 torrent 文件解密 torrent 文件结尾写作背景 最先开始是朋友向我诉说使用某雷下载结果显示因为版权无法下载,找其他的下载器有次数限制,于是来询问我…...

SystemVerilog-时序逻辑建模(5)多个时钟和时钟域交叉
数字硬件建模SystemVerilog-时序逻辑建模(5)多个时钟和时钟域交叉数字门级电路可分为两大类:组合逻辑和时序逻辑。锁存器是组合逻辑和时序逻辑的一个交叉点,在后面会作为单独的主题处理。组合逻辑描述了门级电路,其中逻…...
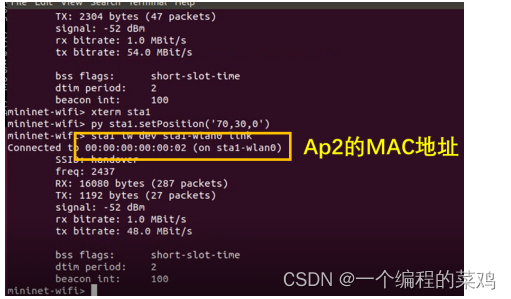
基本中型网络的仿真(RYU+Mininet的SDN架构)-以校园为例
目录 具体问题可以私聊博主 一、设计目标 1.1应用场景介绍 1.2应用场景设计要求 网络配置方式 网络技术要求 网络拓扑要求 互联互通 二、课程设计内容与原理 (1)预期网络拓扑结构和功能 (1)网络设备信息 …...

西北工业大学大学物理(II)期末试题选填解析2021-2022
2 金属薄片,就暗示了载流子是电子了。3 熟练掌握左右手即可。4 又是位移电流。6 感应电场。随时间变化着的磁场能在其周围空间激发一种电场,它能对处于其中的带电粒子施以力的作用,这就是涡旋电场,又叫感生电场。涡旋电场是非保守…...
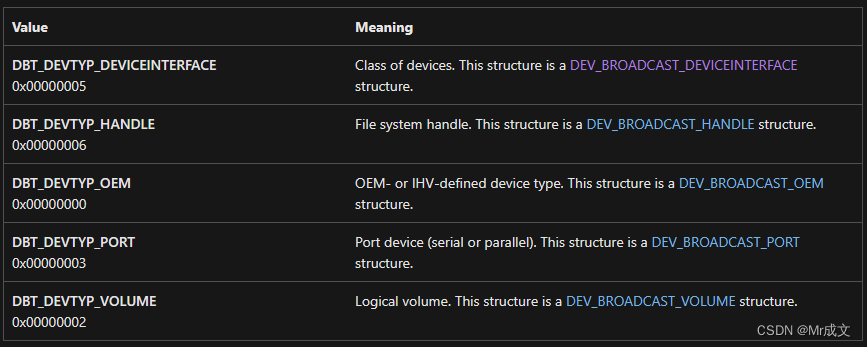
【USB】windows热插拔通知接口分析
文章目录接口介绍概述过滤器介绍举例接收通知创建窗口参考文档接口介绍 概述 window提供了RegisterDeviceNotificationW方法,可以用来监听设备的热插拔事件。 HDEVNOTIFY RegisterDeviceNotificationW([in] HANDLE hRecipient,[in] LPVOID NotificationFilter,[in]…...

CMake入门
课程地址 文档地址 CMake可以用于所有的编程语言 HelloWorld 编写一个C文件: //hello.cpp #include <iostream>int main() {std::cout << "hello, world" <<std::endl;return 0; }手动编译: c hello.cpp书写CMakeList…...

python中一种编写config文件并及时更新的方法
contents0. Intro1. config.py2. 调用以及更新0. Intro 在pytorch或者其他深度学习框架中,有许多超参数需要调整,包括learning_rate,training_data_path等,因此编写一个config文件统一存放这些参数,方便调用/查看/修改…...
基于Windows下离线安装当前最新Arduino ESP32 SDK(2.0.7)固件开发包
基于Windows下离线安装当前最新Arduino ESP32 SDK(2.0.7)固件开发包✨写这篇的文章的初衷,是由于在前几天想通过离线一键安装包方式实现升级安装,结果发现解压后,可以找到开发板,但是无法上传代码ÿ…...
)
Android 9.0 app添加校验锁(输入密码才能进入app)
1.概述 在9.0的系统rom定制化开发中,在一些产品开发中,需要对app启动校验密码,输入密码后,才可以进app,所以说对这种 开发需求,首先找到启动app的关键点以后,在加入限制app启动的弹窗,输入密码,密码正确后在进入app,实现流程 就是这样,接下来看如何实现的 2.app添加校…...

注意力机制详解系列(二):通道注意力机制
👨💻作者简介: 大数据专业硕士在读,CSDN人工智能领域博客专家,阿里云专家博主,专注大数据与人工智能知识分享。 🎉专栏推荐: 目前在写CV方向专栏,更新不限于目标检测、…...

动态规划-规划兼职工作
动态规划-规划兼职工作 一、问题描述 你打算利用空闲时间来做兼职工作赚些零花钱。这里有 n 份兼职工作,每份工作预计从 startTime 开始到 endTime 结束,报酬为 profit。给你一份兼职工作表,包含开始时间 startTime,结束时间 en…...

Redis学习笔记(二)Redis基础(基于5.0.5版本)
一、Redis定位与特性 Redis是一个速度非常快的非关系数据库(non-relational database),用 Key-Value 的形式来存储数据。数据主要存储在内存中,所以Redis的速度非常快,另外Redis也可以将内存中的数据持久化到硬盘上。…...

Ancaonda常用cmd命令总结
1) 查看以创建的虚拟环境: conda info --envs / conda env list 2) 激活创建的环境:conda activate xxx(虚拟环境名称) 3) 退出激活的环境:conda deactivate 4) 删除一个已有虚拟环境:conda remove --name(已创建虚拟…...

yolov5_reid【附代码,行人重识别,可做跨视频人员检测】
该项目利用yolov5reid实现的行人重识别功能,可做跨视频人员检测。 应用场景: 可根据行人的穿着、体貌等特征在视频中进行检索,可以把这个人在各个不同摄像头出现时检测出来。可应用于犯罪嫌疑人检索、寻找走失儿童等。 支持功能:…...
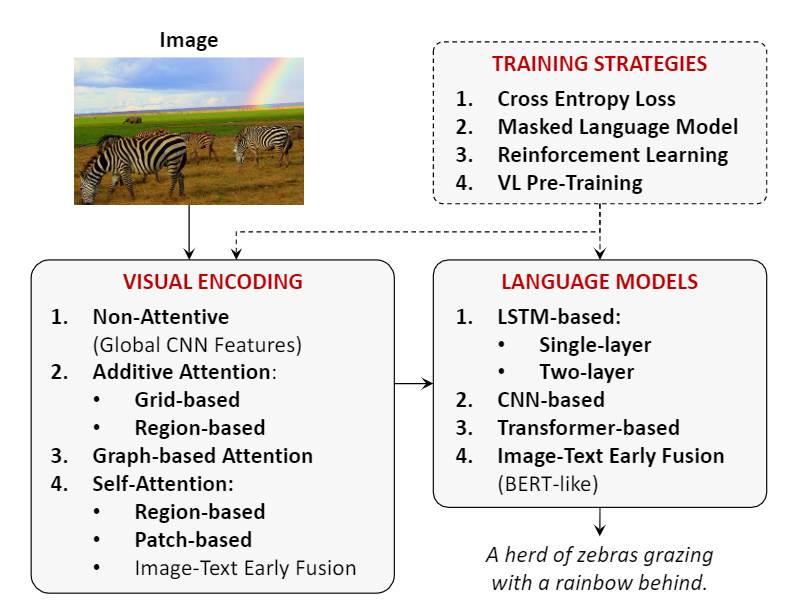
多模态预训练模型综述
经典预训练模型还未完成后续补上预训练模型在NLP和CV上取得巨大成功,学术届借鉴预训练模型>下游任务finetune>prompt训练>人机指令alignment这套模式,利用多模态数据集训练一个大的多模态预训练模型(跨模态信息表示)来解…...

华为OD机试题,用 Java 解【玩牌高手】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...
