57 长短期记忆网络(LSTM)【动手学深度学习v2】
57 长短期记忆网络(LSTM)【动手学深度学习v2】
深度学习学习笔记
学习视频:https://www.bilibili.com/video/BV1JU4y1H7PC/?spm_id_from=autoNext&vd_source=75dce036dc8244310435eaf03de4e330
长短期记忆网络(LSTM)
LSTM 实际中比较常用的网络,LSTM比GRU复杂一些。
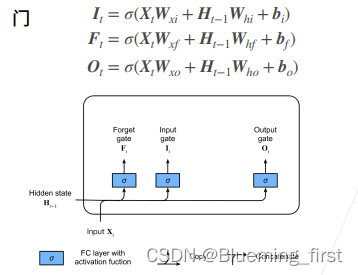
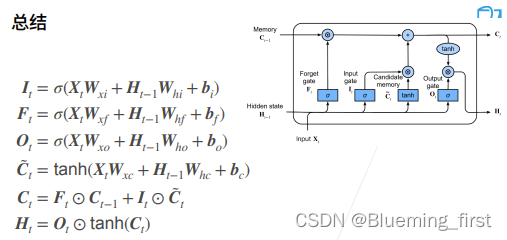
忘记门、输入门、输出门,效果上也是是不是要忘记过去的状态尽量去看现在的输入数据;还是说不看现在的状态尽量去用前一个时刻的状态。

三个门,计算差不多,XW + Ht-1W + b。
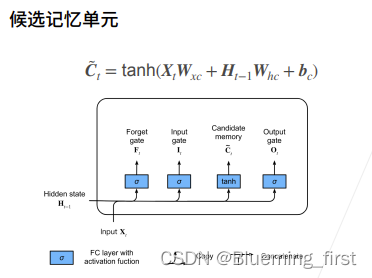
候选记忆单元
C : 之前算RNN里面那个H相似。
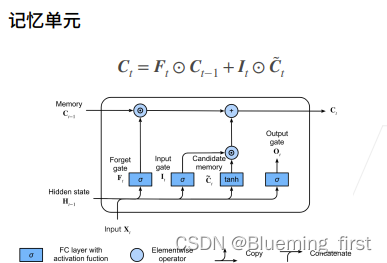
记忆单元
上一个时刻的记忆单元会当做状态传进来,F 尽量不去记住前一个状态 Ct-1,I 尽量去用Ct。
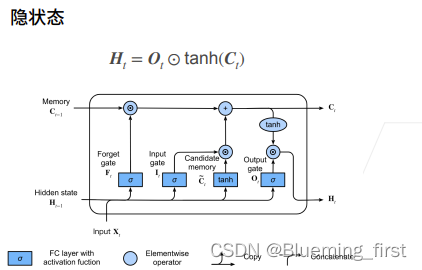
隐藏状态
对候选记忆单元Ct再做一个tanh。
记忆单元处的计算公式,可能将Ct变化为(-2,2),Ht需要在(-1,1)所以需要再做一次tanh,Ot是控制要不要输出(1 输出 ,0 重置不要所有的信息)。
总结:LSTM 和GRU实现效果差不多,但是更加复杂,多了一个C(没有被normalize,所以区间可能会大,忘掉前面的Ct-1,只用当前的Ct),Ht一样可要之前又可不要之前。
相关文章:

57 长短期记忆网络(LSTM)【动手学深度学习v2】
57 长短期记忆网络(LSTM)【动手学深度学习v2】 深度学习学习笔记 学习视频:https://www.bilibili.com/video/BV1JU4y1H7PC/?spm_id_fromautoNext&vd_source75dce036dc8244310435eaf03de4e330 长短期记忆网络(LSTM)…...
算法第十五期——动态规划(DP)之各种背包问题
目录 0、背包问题分类 1、 0/1背包简化版 【代码】 2、0/ 1背包的方案数 【思路】 【做法】 【代码】 空间优化1:交替滚动 空间优化2:自我滚动 3、完全背包 【思路】 【代码】 4、分组背包 核心代码 5、多重背包 多重背包解题思路1:转化…...
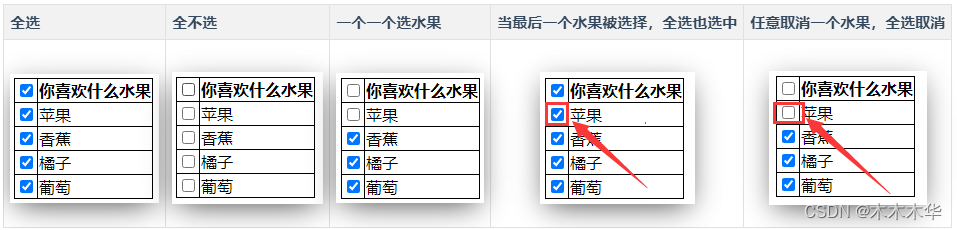
实现复选框全选和全不选的切换
今天,复看了一下JS的菜鸟教程,发现评论里面都是精华呀!! 看到函数这一节,发现就复选框的全选和全不选功能展开了讨论。我感觉挺有意思的,尝试实现了一下。 1. 全选、全不选,两个按钮ÿ…...
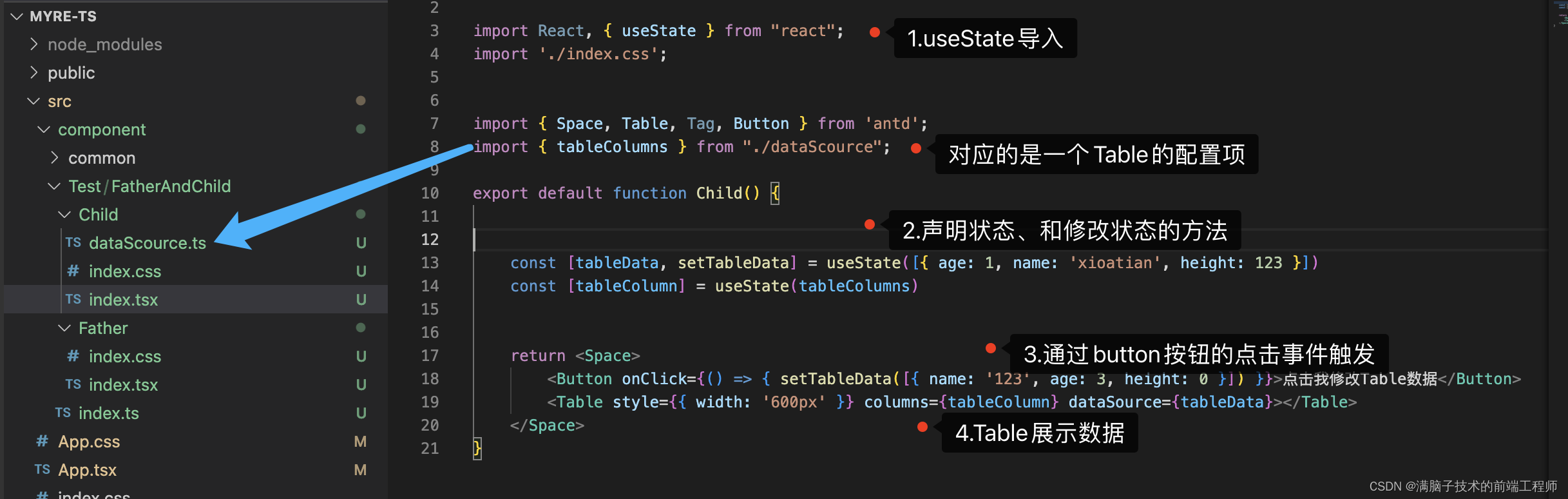
React hooks之useState用法(一)
系列文章目录 学习React已经有很长的一段时间了,今天决定重新回顾一下跟React相关的一些知识点 文章目录系列文章目录结构如下一、hooks是什么?useState可以能做什么二、如何使用useState()第一步:创建【函数组件&…...
spring的简单理解
目录 1 .ioc容器(控制反转) 2. Aop面向切面编程 3. 事务申明 4. 注解的方式启动 5. spring是什么与他的优势 6. 代理设计模式(比如aop) 7. springmvc中相应json数据 8. 使用lombok来进行对代码的简化 9. 使用logback记录…...
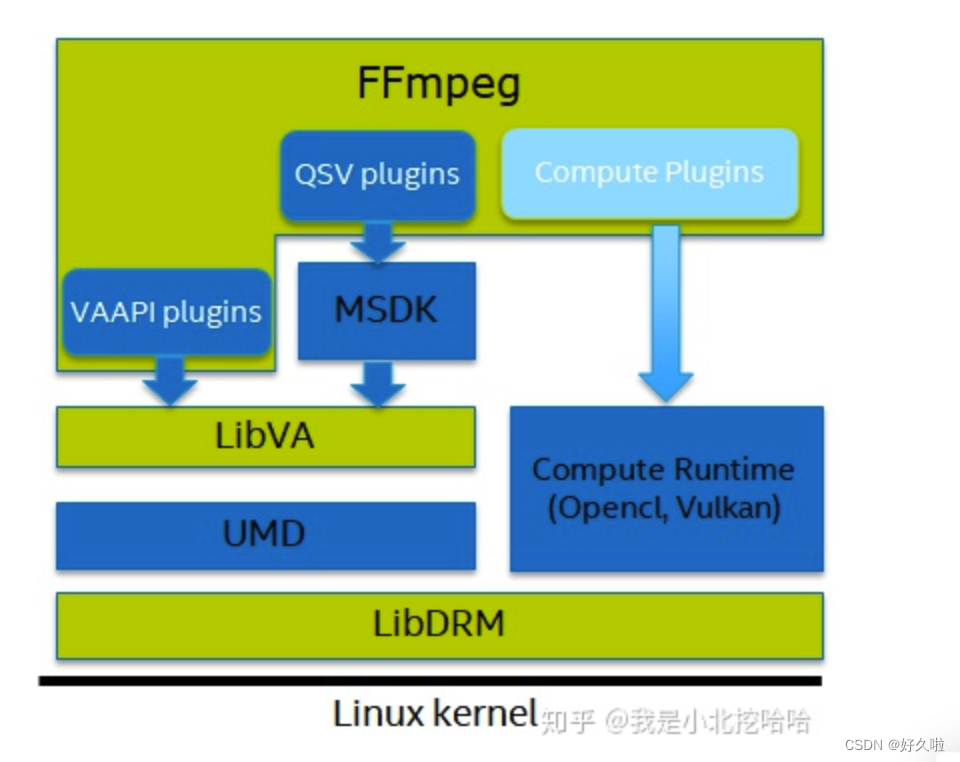
Docker调用Intel集显实现FFmpeg硬解码
文章目录Docker调用Intel集显实现FFmpeg硬解码参考FFmpeg 集成qsv方式一 容器完成所有步骤方式二 容器完成部分步骤方式三 dockerfile部署Docker调用Intel集显实现FFmpeg硬解码 参考 ffmpeg_qsv_docker拉取该镜像可以实现FFmpeg集成vaapi的硬加速,通过dockerfile文…...

端到端模型(end-to-end)与非端到端模型
一、端到端(end to end) 从输入端到输出端会得到一个预测结果,将预测结果和真实结果进行比较得到误差,将误差反向传播到网络的各个层之中,调整网络的权重和参数直到模型收敛或者达到预期的效果为止,中间所…...
uniApp封装一个滑块组件
最近 项目中有一个需求 PC端动态设计的表单 移动端要能渲染出来 那么 就要去找到对应的组件 而其中 没有的 就包括滑块 没有又能怎么办 只能自己封装一个 我们直接上代码 <template><view class"u-slider" tap"onClick" :class"[disabled…...

运动基元(二):贝塞尔曲线
贝塞尔曲线是我第一个深入接触并使用于路径规划的运动基元。N阶贝塞尔曲线具有很多优良的特性,例如端点性、N阶可导性、对称性、曲率连续性、凸包性、几何不变性、仿射不变性以及变差缩减性。本章主要介绍贝塞尔曲线用于运动基元时几个特别有用的特性。 一、贝塞尔曲线的定义 …...

Android 11.0 关于Launcher3中调用截图功能总是返回null的解决方案
1.1概述 在11.0的系统产品开发中,在某些时候需要调用截图接口来进行截屏功能实现,而在Launcher3中发现调用系统截屏接口SurfaceControl.screenshot进行截图的时候始终为null, 获取不到系统当前页面的截屏功能,所以需要找到当前截屏失败的原因然后来实现截屏功能的实现,下面来…...

random随机数
random随机数 1.概述 random用来生成一些随机数,下面介绍random模块提供的方法根据需求生成不同的随机数。 2.random常用操作 2.1.random默认随机数 random()函数返回一个随机的浮点值,默认返回值范围在0 < n < 1.0区间 import randomfor i …...
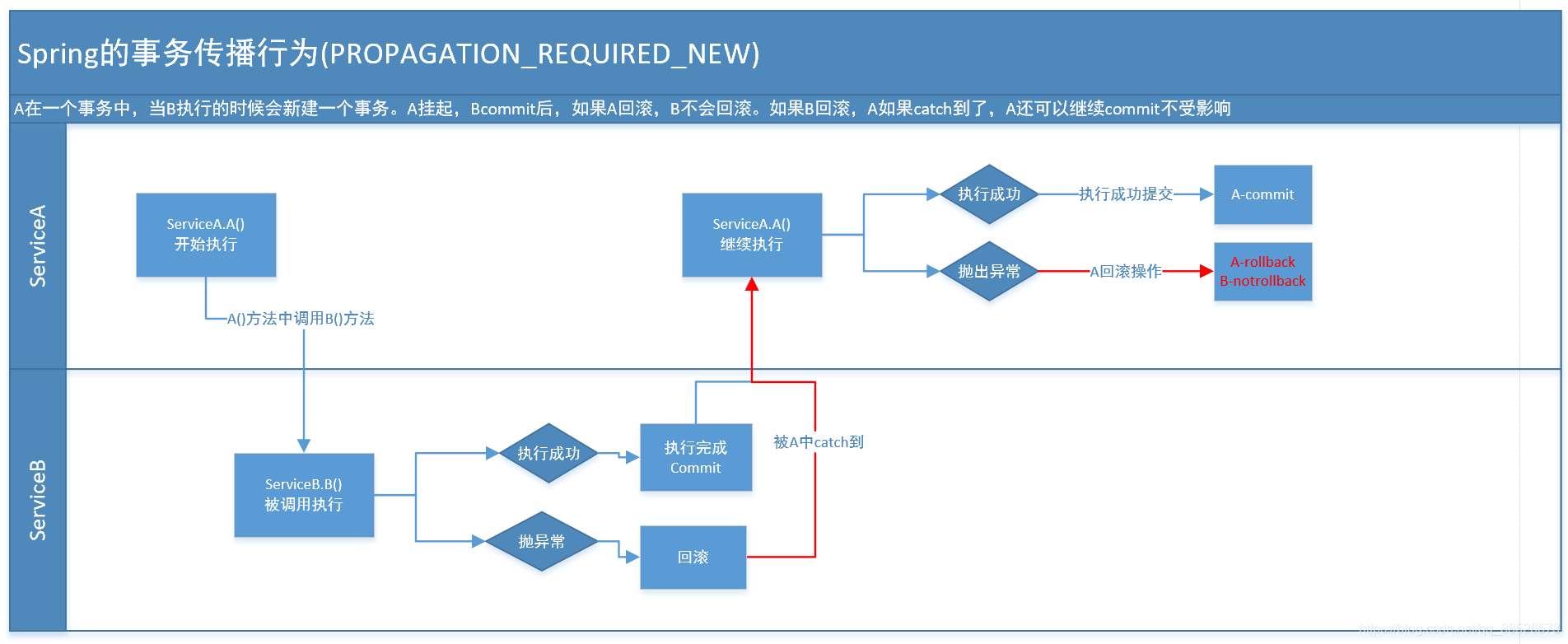
【金三银四系列】Spring面试题-上(2023版)
Spring面试专题 1.Spring应该很熟悉吧?来介绍下你的Spring的理解 有些同学可能会抢答,不熟悉!!! 好了,不开玩笑,面对这个问题我们应该怎么来回答呢?我们给大家梳理这个几个维度来回答 1.1 Spring的发展历程 先介绍…...

linux基本功系列之tar命令实战
文章目录前言一. tar命令介绍二. 语法格式及常用选项三. 参考案例3.1 仅打包不压缩3.2 打包后使用调用压缩命令进行压缩3.3 列出文件的内容3.4 追加文件到tar命令中3.5 释放文件到指定的目录四 . 各种压缩方式的比较总结前言 大家好,又见面了,我是沐风晓…...
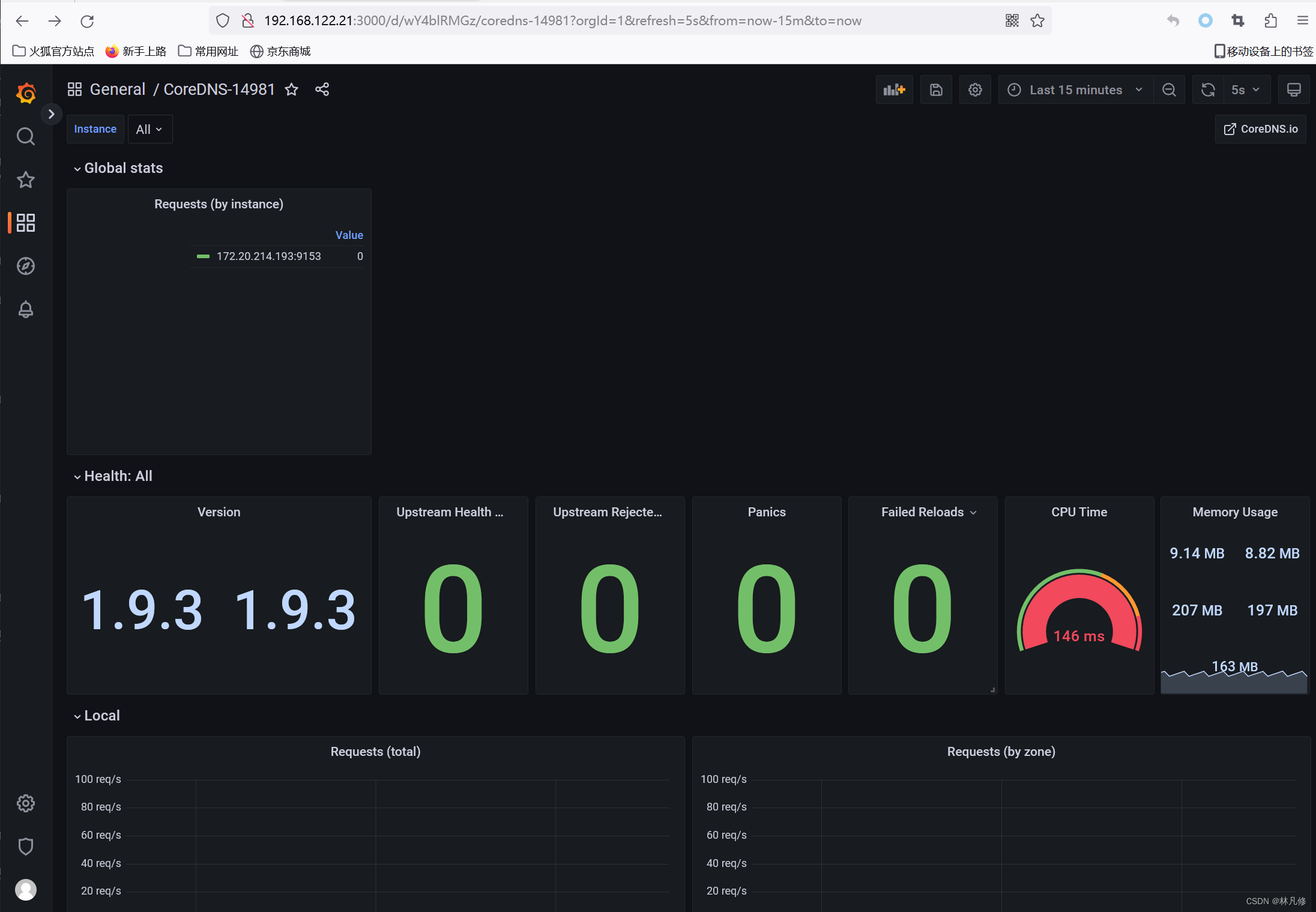
Prometheus服务发现
Prometheus服务发现介绍 Prometheus默认是采用pull的方式拉取监控数据的,每一个被抓取的目标都要暴露一个HTTP接口,prometheus通过这个接口来获取相应的指标数据,这种方式需要由prometheus-server决定采集的目标服务器有哪些,通过…...
【Spring6源码・MVC】请求处理流程源码解析
上一篇《【Spring6源码・MVC】初始化registry,完成url和controller的映射关系》我们知道,在IOC容器加载的同时,初始化了registry这个HashMap,这个HashMap中存放了请求路径和对应的方法。当我们请求进来,会通过这个regi…...

elasticsearch term match 查询
1. 准备数据 PUT h1/doc/1 {"name": "rose","gender": "female","age": 18,"tags": ["白", "漂亮", "高"] }PUT h1/doc/2 {"name": "lila","gender&quo…...
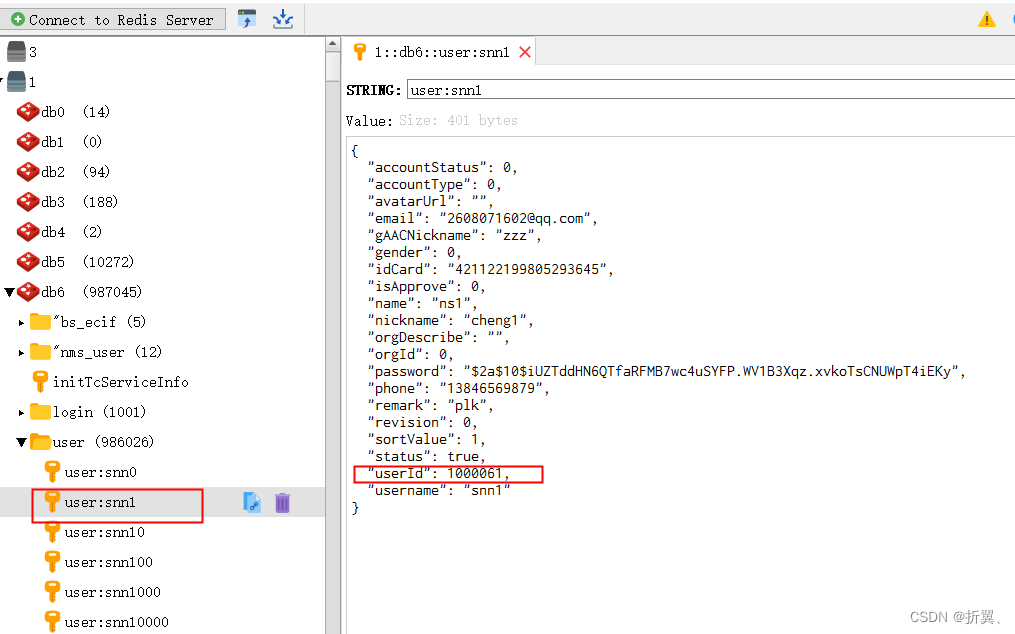
canal使用说明:MySQL、Redis实时数据同步
1. canal简介 canal是阿里开源的数据同步工具,基于bin log可以将数据库同步到其他各类数据库中,目标数据库支持mysql,postgresql,oracle,redis,MQ,ES等 canal分成服务端deployer和客户端adapter,我们可以部署多个,同时为了方便管…...

计算机视觉框架OpenMMLab开源学习(三):图像分类实战
前言:本篇主要偏向图像分类实战部分,使用MMclassification工具进行代码应用,最后对水果分类进行实战演示,本次环境和代码配置部分省略,具体内容建议参考前一篇文章:计算机视觉框架OpenMMLab开源学习&#x…...

awk命令
一.介绍 awk是专门为文本处理设计的编程语言,是一门数据驱动的编程语言。与sed类似,都是以数据驱动的行处理软件,主要用于数据扫描,过滤和汇总。数据可以来自于标准输入,管道或者文件。 二.语法 awk是一种处理文本文件…...

LocalDateTime获取时间的年、月、日、时、分、秒、纳秒
如何把String/Date转成LocalDateTime参考String、Date与LocalDate、LocalTime、LocalDateTime之间互转 String、Date、LocalDateTime、Calendar与时间戳之间互相转化参考String、Date、LocalDateTime、Calendar与时间戳之间互相转化 方法介绍 getYear() 获取日期的年 getMon…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
