论文-分布式-分布式计算|容错-分布式控制下的自稳定系统
- 参考文献
- Self-stabilizing systems in spite of distributed control
- 可以把松散耦合的 循环序列过程 间的同步任务,看成是要保持一个这样的不变性:“系统要处于一种合法状态”
- 因此每个进程在运行每一个可能会改变不变性的步骤之前都要先检查一下是可以执行,还是要延迟执行
- 如果允许不同进程互斥地访问记录有“当前系统状态”的公共存储,解决方案就很简洁—并且可以很系统化地实现
- 如果没有一个所有进程都可以访问的公共存储模块的话,复杂度就会增加,因为当前系统的状态就不得不分布式地存储在各个进程内的变量中;
- 进一步地,如果再对通信进行限定,比如每个进程只能与它的邻居进行通信,复杂度还会上升
- 问题的复杂性在于单个进程的状态只能被整个系统状态中对它可用的那一部分影响,而进程本地动作要基于本地信息实现全局性的目标
- 这样的系统(可以称之为“分布式控制”系统)已经被设计出来,但是当时所知的所有设计都不是“自稳定”的,也就是说它们一旦进入非法状态,就会永远处于这种状态
- 考虑一个由少数边连接的图,图中每个节点对应一个有限状态机;
- 图中直接相连的那些状态机,它们相互之间称为邻居
- 每个状态机定义一个或多个"特权",比如是关于它自己和邻居状态的一组布尔函数;
- 当布尔函数值为 true 时,我们就认为对应的特权“存在”
- 我们引入一个中央守护进程,采用中央守护进程只是为了方便说明,实际上可以采用一个分布式的 守护进程 来完成,具体算法本文没有涉及
- 一个简单的观察是如果享有 特权 的是不相邻的状态机,它们的转换是可以并行进行的,它们不需要同步,因为并行运行的结果与通过一个中央守护进程选择一个进行执行是一致的,因为选择一个执行之后,由于它们两个不相邻,因此另一个的邻居状态不会改变,在新的状态中另一个依然是享有特权者,下一次可以继续选择它,而相邻的实际上因为可以相互通信,它们自己可以协调到底是谁进行状态转换
- 在下面的状态转换手动演练中,实际上我们就充当了中央守护进程的角色,在有多个 特权 存在的情况下,选择其中一个进行状态转换,通过它从“存在”的 特权 中选择一个进行状态转换,每个合法状态中可能有多个特权“存在”,所以需要从里面选择一个进行状态转换
- 允许多个享有特权者是一种更通用的需求,只有一个享有特权者的情况是互斥锁,而多个则可以类比信号量
- 拥有该被选定的 特权 的状态机可以进行状态转换—根据一个以它的老状态和邻居状态为输入的状态函数进入新状态
- 对于不止有一个 特权“存在”的状态机来说,新状态可能还依赖于被选定的特权
- 状态转换完成后,守护进程再选择一个新的特权
- 可以通过如下全局规则判断系统是否处于合法状态
- 要求:
- 1. 每个合法状态,必须至少要有一个 特权“存在”
- 2. 在合法状态的每一个执行步骤都要确保系统还是会处于合法状态
- 3. 每个 特权 至少出现在一个合法状态中
- 4. 对于任意两个合法状态来说,总是可以通过一定执行步骤从一个到达另一个
- 我们称一个系统是“自稳定”的,当且仅当无论系统初始状态如何也无论每次为下一个执行步骤选定的 特权 是谁,可以保证在有限数目的执行步骤之后总是至少存在一个 特权 并且系统可以发现它自己处于合法状态
- “自稳定”的系统是否能通过各节点的本地执行步骤来满足上述的全局性条件,本来也不是可以很直接地得出结论
- 而守护进程的不确定性引入了额外的复杂度
- 实际上该问题可以通过如下三个方案解决:
- 在如下三个解决方案中,我们假设有 N+1 个进程,它们以 0…N 进行编号
- 假设当前机器编号为 nr.i
- L,代表机器的左邻居的状态,对应的机器编号为 nr.(i-1) mod (N+1)
- S,代表当前机器自己的状态,编号为 nr.i
- R,代表机器的右邻居的状态,对应的机器编号为 nr.(i+1) mod (N+1)
- 换句话说,我们假设机器是像环一样连接在一块
- 机器 nr.0 又称为“底部机器”,机器 nr.N 则又被称为“顶部机器”
- 同时在这里我们将那些只有一个 特权“存在”的状态作为合法状态
- 同时所有的方案描述,均采用了如下格式:
- “if privilege then corresponding move fi” 如果有特权,那么就进行相应的操作
- Solution with K-state Machines (K>N)
- 每个机器的状态由一个整数 S 表示,并且0=<S<K
- 对于每个机器来说,只定义一个 特权,具体如下:
- 对于底部机器来说,if L = S then S := (S+1)mod K fi
- 对于其他机器来说,if L != S then S := L fi
- 说明 1:对于一个中央式的守护进程来说,K>=N 就可以了
- 说明 2:C.S.Scholten 扩展了该解决方案,使之可以应用到任意网络结构
- 根据格式“if privilege then corresponding move fi”,我们可以看出,在上面的解决方案中,对于 底部机器 来说 L=S 就是 特权,意味着如果 L=S 它就是享有特权者,对于其他机器来说 L!=S 就是 特权,意味着如果 L!=S 它就是享有特权者
- 我们可以以 3 个状态机为例,令 K=4,根据上面的算法进行模拟运行可以发现,即使一开始不满足有一个特权者,执行一段时间后会进入只有一个特权者的状态,并且此后一直处于只有一个特权者的状态
- 比如如下状态转换序列,如下数组中的值分别代表编号为 0,1,2 的状态机的状态值
- [0, 1, 2] -> [0, 0, 2] -> [0, 0, 0] -> [1, 0, 0] -> [1, 1, 0] -> [1, 1, 1] -> [2, 1, 1] -> [2, 2, 1] -> [2, 2, 2]……
- 如上,初始状态状态机 0,1,2 对应的 S 值为[0, 1, 2]
- 根据方案描述:
- 对于状态 1 来说状态值是 1,左右值分别是 0 和 2,因此满足 L!=S,所以此时状态机 1 享有特权
- 对于状态机 2 来说状态值是 2,左右值分别是 1 和 0,因此也满足 L!=S,因此它也是享有特权者
- 对于 0 来说,要看 L 是否等于 S,由于 0 的左右值是 2和 1,因此它不享有特权
- 可以看到这个初始状态,有两个享有特权者,不满足上面关于合法状态中只有一个特权者的定义
- 然后我们根据状态转换函数,从初始状态开始不断进行状态转换,可以看到到了[0, 0, 0]后,变成了只有状态机 0为特权者,而此后就一直处于只有一个享有特权者的状态
- 可以看到整个过程中,就是从初始处于非法状态,然后经过一定步骤进入了合法状态,此后就一直处于合法状态
- 而这个过程中,进程只看了它左右邻居的状态,通过局部信息就实现了只有一个享有特权者这一全局性需求
- 这实际上说明了在分布式系统中,我们仅通过部分节点的局部信息不需要得到全局状态,就可以实现全局性的状态要求
- 其他两个方案代表的含义与上述解决方案类似,有个区别是状态机定义了两个特权
- 以第三个方案为例,我们再手动模拟一个状态转换过程,假设有 4 个状态机,它们的初始状态值分别为[0,1,2,0]:
- 按照下面的算法描述,可以得到如下一个状态转换过程
- [0,1,2,0] 此时 0,1,2 均为享有特权者,选择 0 进行状态转换
- [2,1,2,0] 此时 1,2 为享有特权者,选择 1 进行状态转换
- [2,2,2,0] 此时 2,3 为享有特权者,选择 2 进行状态转换
- [2,2,0,0] 此时 1 为享有特权者,1 进行状态转换
- [2,0,0,0] 此时 0 为享有特权者,0 进行状态转换……
- 可以看到,依然是初始不合法,然后一定步骤后变成合法,之后一直合法
- 方案 3 具体算法如下:

- 上述三个解决方案说明:对于一个分布式系统来言,即使节点只能跟所有节点中的部分节点进行通信,对于上述特权者(互斥,任意时刻只有一个特权者)问题而言,存在一个“自稳定”的算法
- 无论系统初始状态如何,经历一定步骤之后它都可以进入合法状态
- “自稳定”属性使得分布式算法可以从暂态错误中恢复
- Dijskstra 在论文中提出了“自稳定”概念,并以上述“令牌环”问题为例给出了相应的自稳定算法
- 在“令牌环”场景下,计算机网络连接成环状,每个计算机可以获取它前面的那个计算机的状态,该状态可以显示该计算机“持有令牌”还是“不持有令牌”
- 对应的算法要满足如下两个条件:
- 1.任意时刻只有一个计算机持有令牌
- 2.持有令牌的计算机会将令牌传给它后面的计算机,最终该令牌可以在环上循环流转
- 不持有令牌对于单个计算机来说是合法的,但是如果所有计算机都不持有令牌,对于整个系统来说就是非法的
- 类似的,如果有不止一个计算机持有令牌,也是非法的,但是对于每个计算机来说这很难发现,因为他们每个都只能与邻居通信
- 因此,论文中的算法并没有去检测错误,而是确保系统不断向着合法状态前进
- 而且那个时候用于错误检测的传统方法很困难而且很耗时
- 但是随着新的更高效的错误检测算法的提出,基于错误检测还可以将非自稳定算法结合自稳定算法实现更高效的自稳定算法
相关文章:

论文-分布式-分布式计算|容错-分布式控制下的自稳定系统
参考文献Self-stabilizing systems in spite of distributed control可以把松散耦合的 循环序列过程 间的同步任务,看成是要保持一个这样的不变性:“系统要处于一种合法状态”因此每个进程在运行每一个可能会改变不变性的步骤之前都要先检查一下是可以执…...

C#压缩图片的方法
/// <summary> /// 图片压缩 /// </summary> /// <param name"imagePath">图片文件路径</param> /// <param name"targetFolder">保存文件夹</param> /// <param name"quality">压缩质量</param&g…...

安装 fcitx + 搜狗/谷歌输入法 之后导致 死机,重启后黑屏只有鼠标可以移动
一般的原因就是 : fcitx 导致的问题 方法就是 先卸载搜狗,再卸载fcitx 解决办法: 首先:ctrlaltF6 进入命令行界面,如果进不去就 ctrlaltF2 接下来执行: sudo apt-get remove sogoupinyin sudo apt-get …...

Maven项目转为SpringBoot项目
Maven项目转为SpringBoot项目 前言创建一个maven项目前的软件的一些通用设置Maven仓库的设置其他的设置字符编码编译器注解支持 创建的Maven项目修改为Spring Boot项目修改pom.xml文件修改启动类-Main新建WAR包所需的类 添加核心配置文件 测试的控制器最后整个项目的目录结构
C语言之预处理
目录 前言 宏定义define的用法 文件包含include的用法 条件编译的用法 其他预处理命令 练习题 练习一 练习二 练习三 前言 预处理命令可以改变程序设计环境,提高编程效率,它们并不是C语言本身的组成部分,不能直接对它们进行编译&am…...

css步骤条
html 代码以及样式 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>css步骤条</title><style>.steps {display: flex;justify-content: space-between;padding: 0;margin: 20px 10px;lis…...

[Hive] 常见函数
文章目录 字符串函数数值函数随机函数日期和时间函数字符串转时间 聚合函数数组函数结构体函数数组函数映射函数 map正则处理JSON 字符串函数 CONCAT(string1, string2, …):将多个字符串连接成一个字符串。 LENGTH(string):返回字符串的长度。 LOWER…...

Mac用NTFS文件夹读写NTFS硬盘 NTFS能复制多大的文件
Mac作为一款备受欢迎的计算机操作系统,具备了许多令人惊叹的功能和特性。然而,对于一些Mac用户来说,使用NTFS格式的硬盘可能存在一些疑问。他们可能想知道Mac是否能够读写NTFS格式的硬盘,以及NTFS格式的硬盘是否有文件大小的限制。…...
【unity3D】Scroll Rect组件—制作下滑列表
💗 未来的游戏开发程序媛,现在的努力学习菜鸡 💦本专栏是我关于游戏开发的学习笔记 🈶本篇是unity的Scroll Rect组件 Scroll Rect组件 基础知识详细说明案例演示——制作一个简单的下滑框扩展 介绍:Scroll Rect组件是用…...
网络扫描与网络监听
前言:前文给大家介绍了网络安全相关方面的基础知识体系,以及什么是黑客,本篇文章笔者就给大家带来“黑客攻击五部曲”中的网络扫描和网络监听 目录 黑客攻击五部曲 网络扫描 按扫描策略分类 按照扫描方式分类 被动式策略 系统用户扫描 …...
 C)
Codeforces Round 904 (Div. 2) C
C. Medium Design 思路:我们设最大值所在的下标为 x x x,最小值所在的下标为 y y y,那么我们考虑一段区间对于答案的贡献: 若一段区间覆盖了 x x x,但没有覆盖 y y y,那么这段区间需要选择 若一段区间覆盖了 y y y,但没有覆盖 x…...
DBeaver连接数据库报错:Public Key Retrieval is not allowed 的解决方案
写在前面: DBeaver是一款免费的数据库管理工具,安装也是傻瓜式一键安装,比较推荐。 DBeaver官网(加载有点慢,耐心等待):DBeaver Community | Free Universal Database Tool 报错详情ÿ…...

DeepFace【部署 04】轻量级人脸识别和面部属性分析框架deepface使用Docker部署CPU+GPU两个版本及cuDNN安装
使用Docker部署CPUGPU 1.CPU2.GPU3.cuDNN安装3.1 Prerequisites3.2 下载Linux版本cuDNN3.3 安装 1.CPU 本说明基于DeepFace的Docker镜像文件deepface_image.tar进行说明。 # 1.导入镜像 docker load -i deepface_image.tar# 2.创建模型文件夹【并将下载好的模型文件上传】 mk…...

程序生活 - 减肥小记
文章目录 缘起健康就好了吗?关于外在和物质生活难与易 我的减肥生活一些细节轻断食戒糖、油炸、重口味睡眠改变社交方式用运动化解压力不喝牛奶 缘起 2017年的一次腿受伤,让我从一个怎么都吃不胖的人,变成了一个实实在在的胖子。 如果你从来…...
深度学习_4_实战_直线最优解
梯度 实战 代码: # %matplotlib inline import random import torch import matplotlib.pyplot as plt # from d21 import torch as d21def synthetic_data(w, b, num_examples):"""生成 Y XW b 噪声。"""X torch.normal(0,…...
)
《视觉SLAM十四讲》公式推导(三)
文章目录 CH3-8 证明旋转后的四元数虚部为零,实部为罗德里格斯公式结果 CH4 李群与李代数CH4-1 SO(3) 上的指数映射CH4-2 SE(3) 上的指数映射CH4-3 李代数求导对极几何:本质矩阵奇异值分解矩阵内积和迹 CH3-8 证明旋转后的四元数虚部为零,实部…...

pnpm、npm、yarn的区别
pnpm、npm、yarn是三种不同的包管理器,它们之间有一些区别。 安装速度:pnpm的安装速度比npm和yarn快,因为它使用了只下载必需的模块,而不是下载整个依赖树。此外,pnpm还可以并行下载模块,从而进一步提高下…...
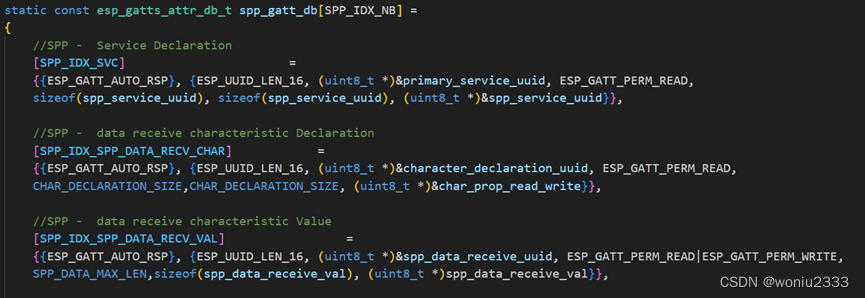
搞定蓝牙——第四章(GATT协议)
搞定蓝牙——第四章(GATT协议) 原理介绍层次结构server和client端Attribute ESP32代码 文章下面用的英文表示: server和client:服务端和客户端 char.:characteristic缩写,特征 Attribute:属性 ATT:Attribut…...

Go语言入门心法(十四): Go操作Redis实战
Go语言入门心法(一): 基础语法 Go语言入门心法(二): 结构体 Go语言入门心法(三): 接口 Go语言入门心法(四): 异常体系 Go语言入门心法(五): 函数 Go语言入门心法(六): HTTP面向客户端|服务端编程 Go语言入门心法(七): 并发与通道 Go语言入门心法(八): mysql驱动安装报错o…...
)
Java学习笔记(三)
前言 这个主要就是想记录一个点,就是二维数组保存的元素就是一维数组的地址,这个概念大家都知道了,那么接下来就是我最近写程序发生的一个事情了。 随机打乱一个一维数组 这个程序我相信大家都是会写的,通过randomArr来随机打乱…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解
在我的上一篇博客:基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目,该项目展示了一个强大的框架,旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人,更是一个集…...
