支持向量机(SVM)
一. 什么是SVM
1. 简介
SVM,曾经是一个特别火爆的概念。它的中文名:支持向量机(Support Vector Machine, 简称SVM)。因为它红极一时,所以关于它的资料特别多,而且杂乱。虽然如此,只要把握住SVM的一些特点,至少可以做到思路清晰。
(1)首先,SVM是按照监督类学习方式进行运作的。即:数据当中含有目标值。
(2)SVM采用监督学习方式,对数据进行二分类(这点跟逻辑回归一样)。但是,SVM和逻辑回归(LR)有有很多不同点。我们先看看相同点:
- 二者都是线性分类器
- 二者都是监督学习算法
- 都属于判别模型(KNN, SVM, LR都属于判别模型),所谓判别模型就是指:通过决策函数,判别各个样本之间的差别来进行分类。
不同点就很多了,现在先列举一些,LR之前已经介绍过,关于SVM的具体理论先放到后面
-
二者的损失函数和目标函数不一样。
-
二者对数据和参数的敏感度不同。SVM由于采用了类似于“过度边界”的方式,泛化能力更好
SVM可以作线性分类器,但是在引入核函数(Kernel Method)之后,也可以进行非线性分类
2.SVM分类
SVM大体上可分为:
- 线性可分SVM:大体就是指一条线,把样本分成两份这种,我们会先从这个入手,这个相关理论懂了,后面的就会很简单
- 线性SVM
- 非线性SVM(需要核函数的支持)
二. 详细介绍
1. 线性可分SVM
1.1 支撑点,支撑向量
这个将作为重点来理解,这个相关理论知道了,那么,剩下的就很好理解,首先,我们先看一张图,然后我们根据这张图引出两个概念:支撑点,支撑向量。
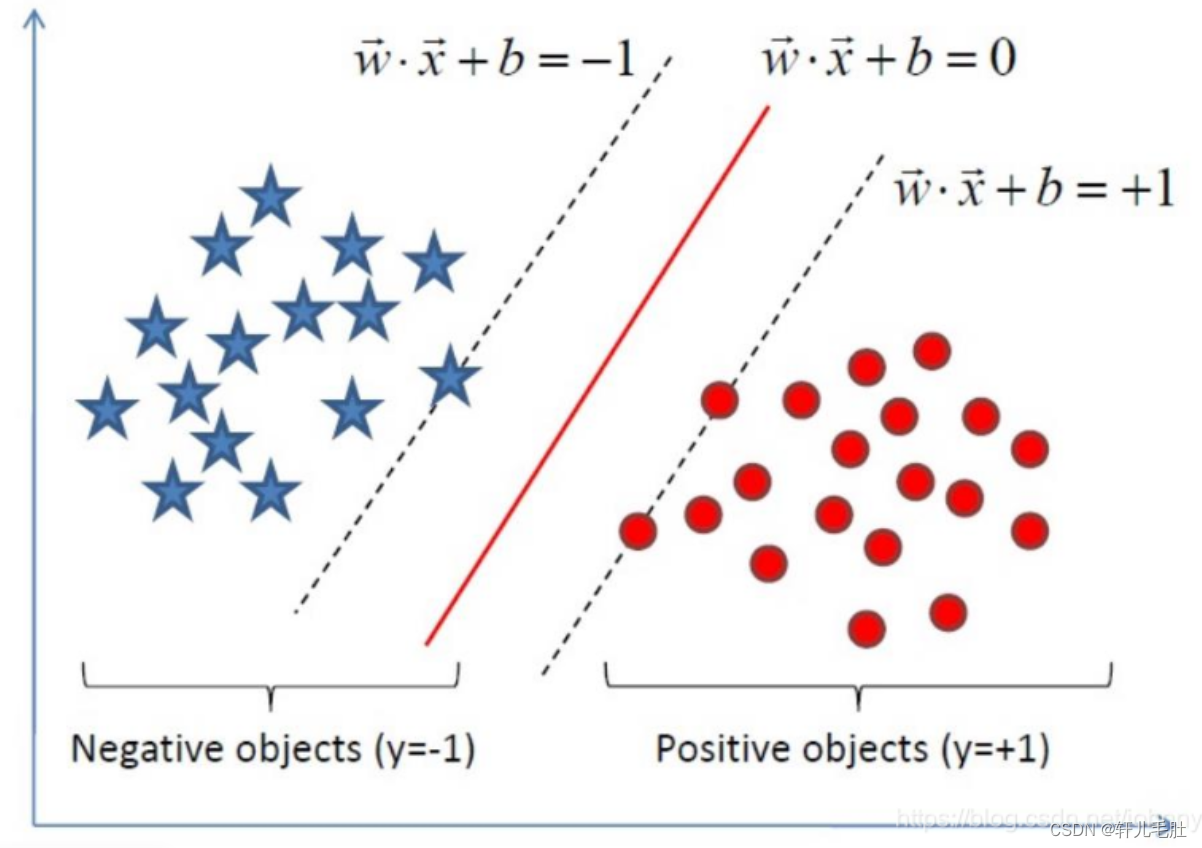 图一
图一
我们看看图上面的三条线,首先,这是个二维平面,因此分割线可以表示成线性函数的形式:
![]()
关于w,它其实是一个权值向量,它可以表示成如下的形式,至于说为什么能够这么表示,我们一会儿再说。

在上图中,两个虚线之间,我们可以当做一个“过度区域”,在虚线上面,有一个蓝色的点,和两个红色的点正好位于虚线上面。对于这3个样本,我们标号1,2,3。我们大可以让alpha1,alpha2, alpha3不为0,其他的点alpha都是0。为什么可以这么做呢?因为边界的划定,也就是虚线,只受这三个边界点的影响(即:影响w向量)我们在现实中直接调整这三个边界点的alpha值,就可以确定界限。那么这三个点,我们就可以称他们为:**支撑点 **
如果你确定了一个起始点,那么起始点到各个点之间可以组成向量,这个起始点到支撑点之间就可以组成一个个:支撑向量
1.2 分割超平面与间隔最大化
首先,我们得知道什么是超平面?一般来说,二维就可以组成一个平面,那么如果是多维的呢?一般把超过二维的,就叫做超平面。由于超平面本身超出了一般人的认知,所以我们在理解分割超平面的时候,还是以最简单的二维平面入手,然后进行扩展。
在了解了什么是超平面之后,我们看这样一个图:

在这幅图中,我们看到了如此多的分割线,这些分割线都成功的把黑点和白点给区分开了。即:都把类别给分对了。那么,哪条线才是最优的呢?(如何分割超平面,就是解决这个问题)
我们就直接在二维空间一个基本问题入手:点到直线的距离入手。
我们假设有这么一条线:
![]()
再给定一个点(x0, y0)那么这个点到直线的距离就是:
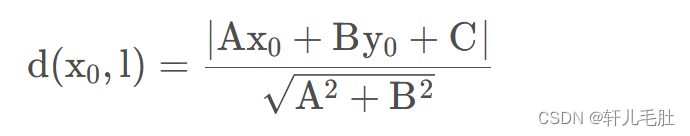
然后我们在此基础上直接把分子的绝对值给去掉,去掉之后,运算结果就会有正负之分了,通过正负,可以判断这个点在这条直线的哪一侧。然后各个项给拆开如下:
![]()
我们令各项系数分别记为:A’, B’ C’。然后整个公式就可以写成向量相乘的形式:
![]()
我们直接把(A’,B’)记为wi向量,将后面的(x0,y0)记为x向量 C’可以记为b,于是就得到了上述式子。
在这个例子当中,只是给了一个二维平面,实际情况下,有可能是多维的。此时w向量也是多维的,可以记为w = (w1,w2,w3……wn),其中这里的w1, w2对应的就是上面式子当中的A, B。我们再回过头看点到直线距离公式,看看那个分母。大致就可以猜出来一件事情:在多维空间中一个点到一个线的距离是: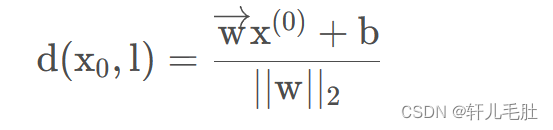
此时,我们再看看图一。注意,图一两条虚线线等号后面分别是+1,-1,为啥是这个呢?
假设我划分了一个线,那么显然,每一个点到这个线都会有一个距离,按照上面这个式子,求出来的距离是带有符号的,这个时候就体现出这个1,-1的价值。这个1,-1,也是y(i)值。如果,求出的是正的,那么乘以1,就是距离本身,如果d为负值,那么乘以-1,又转回正的,还是距离。这就是为什么真正的距离会写成

那么,我所有点,都跟这个直线求一个距离,最后取一个最小值。
我跟所有的直线,都做上面这个操作,就会得到若干个这样的最小值,然后我取最小值最大的那个直线,就是最优解。即:
![]()
对于这个方式,有一个很直观的名字:间隔最大化。
以上就是对分割超平面的一种直观的解释的一个解释。如果扩展到多维,即:超平面,很多时候,我们就不能用单纯一个x向量来解释了。其实,二维当中y与x是线性关系,也是一种映射关系。在多维平面当中,这种映射往往比较复杂,因此,扩展之后,我们会把间隔最大化的线写成如下形式:![]()
其中,φ(x)是某个确定的特征空间转换函数,它的作用是将x映射到(更高的)维度。而在最简单的二维平面中φ(x)=x
由于在线性可分SVM是用来做分类问题,最基本的就是用来做二分类问题,所以,还要把上面这个式子映射到一个只有两个取值的函数当中,这就是线性可分SVM的决策函数:
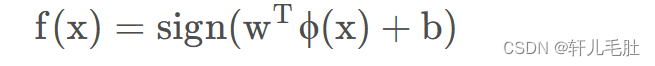
1.3 线性可分SVM的目标函数以及相关算法
我们在图一当中,知道,虚线部分的y值取1,或者-1。但实际上,支撑点可不一定满足这个条件,类似的例子,可以举出无数个。因此,对于目标函数的构建,我们首先就要考虑一个问题:缩放。
根据题设,我们有一个间隔最大化的函数:
![]()
我们要让y(x)满足这个条件:
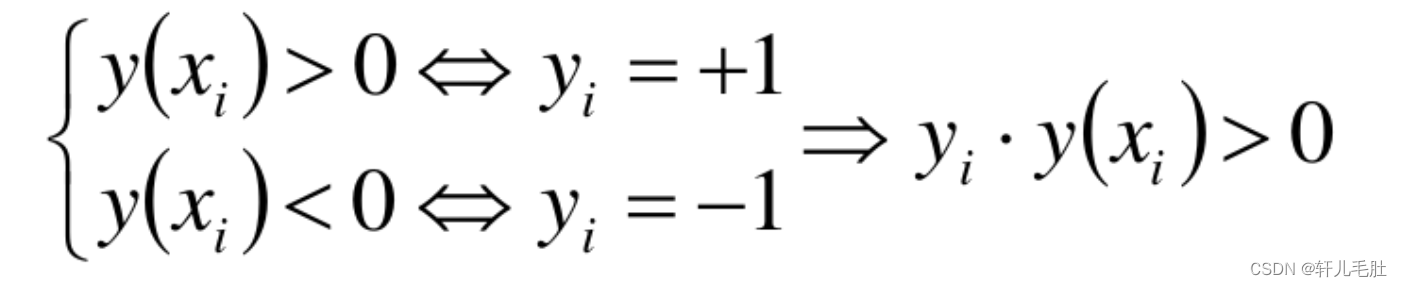
我们对w和b进行等比缩放,就得到了(回过头看看公式(一)):

于是,把这个与公式二结合起来看,我们就得到了目标函数:
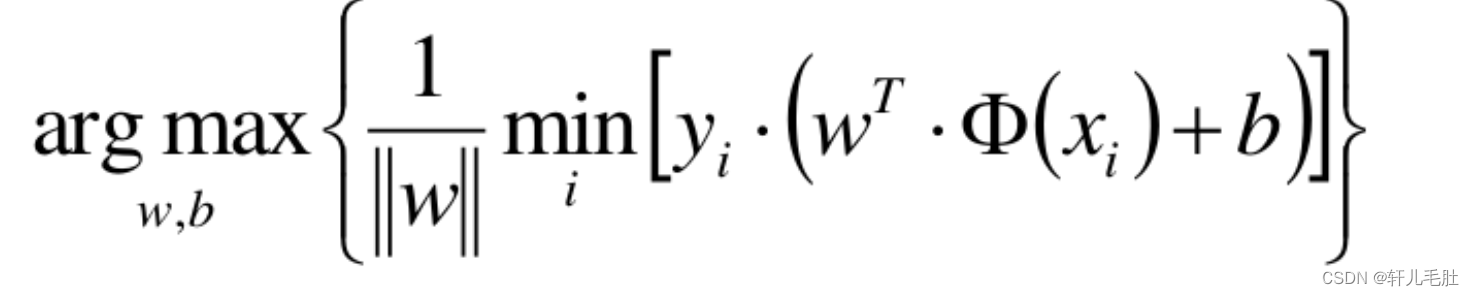
缩放的理论知道了,我们下一步,就是想,怎么能让那个y值是1。对于分类来说,就是让各个类别的点,尽量远离过渡区域,也就是说,这些点离分割线的距离要大于或者等于1,这样才达到分类目的,如下图所示:那个margin大于1,分类才越准确。
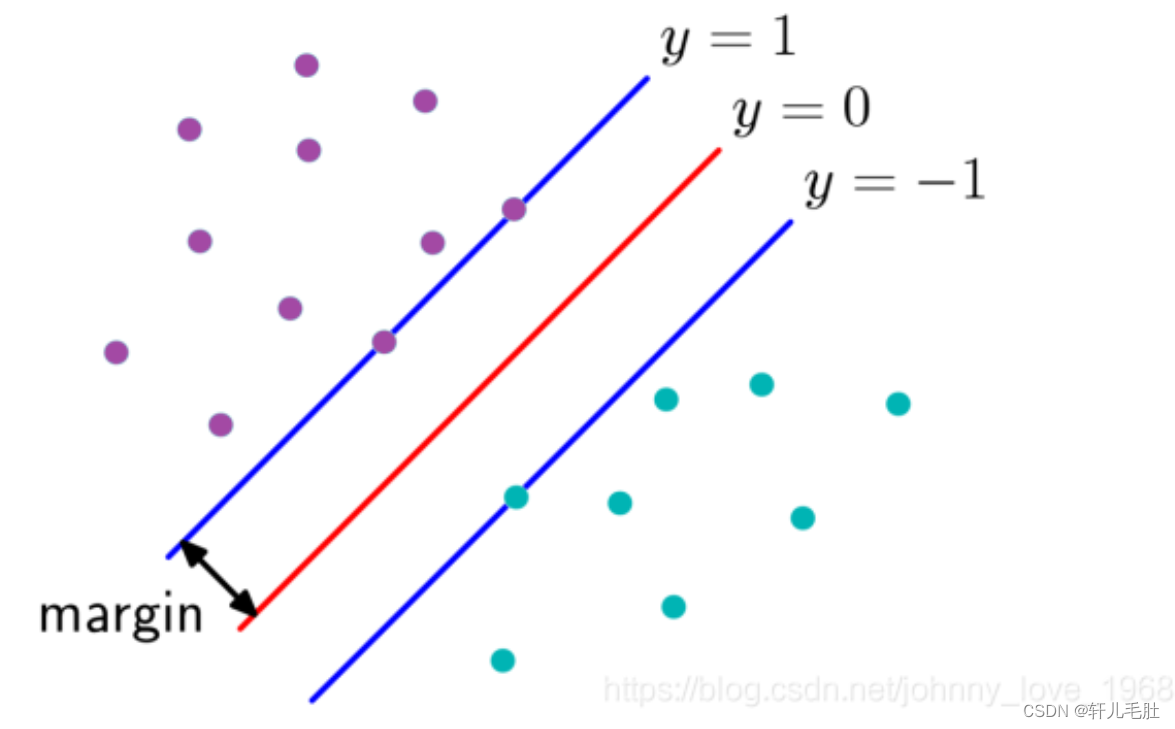
用符号表示就是:
通过等比例缩放w的方法,使得两类点的函数值都满足| y |≥1
然后,我们把间隔函数代入:
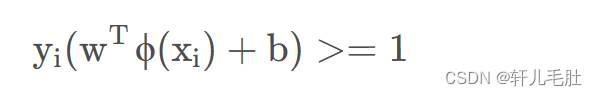





(公式三)
那么,我们就可继续用拉格朗日乘数法进行求解,然后,就求出了alpha*
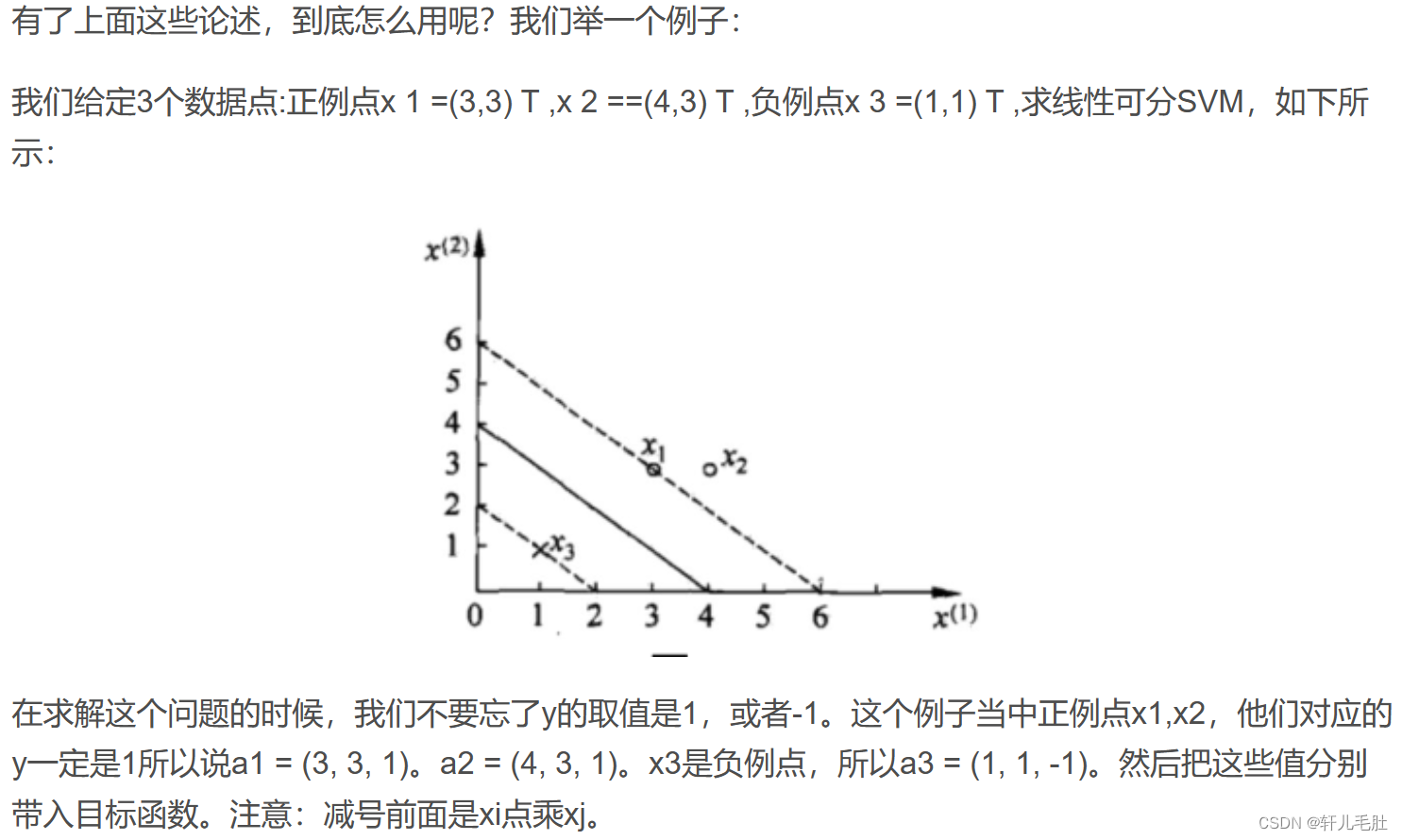
1.4 线性可分SVM的简单举例


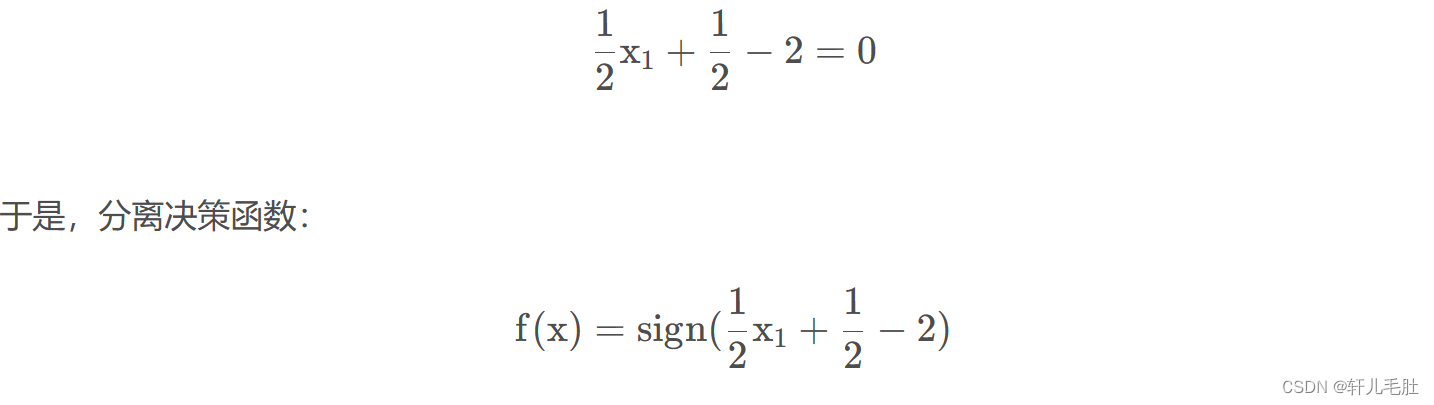
2.线性SVM
2.1 为什么需要线性SVM
在实际运用当中,首先,即使数据是线性可分的。通过线性可分SVM得到的分离超平面也不一定就是最适合的。比如说下面这个图:
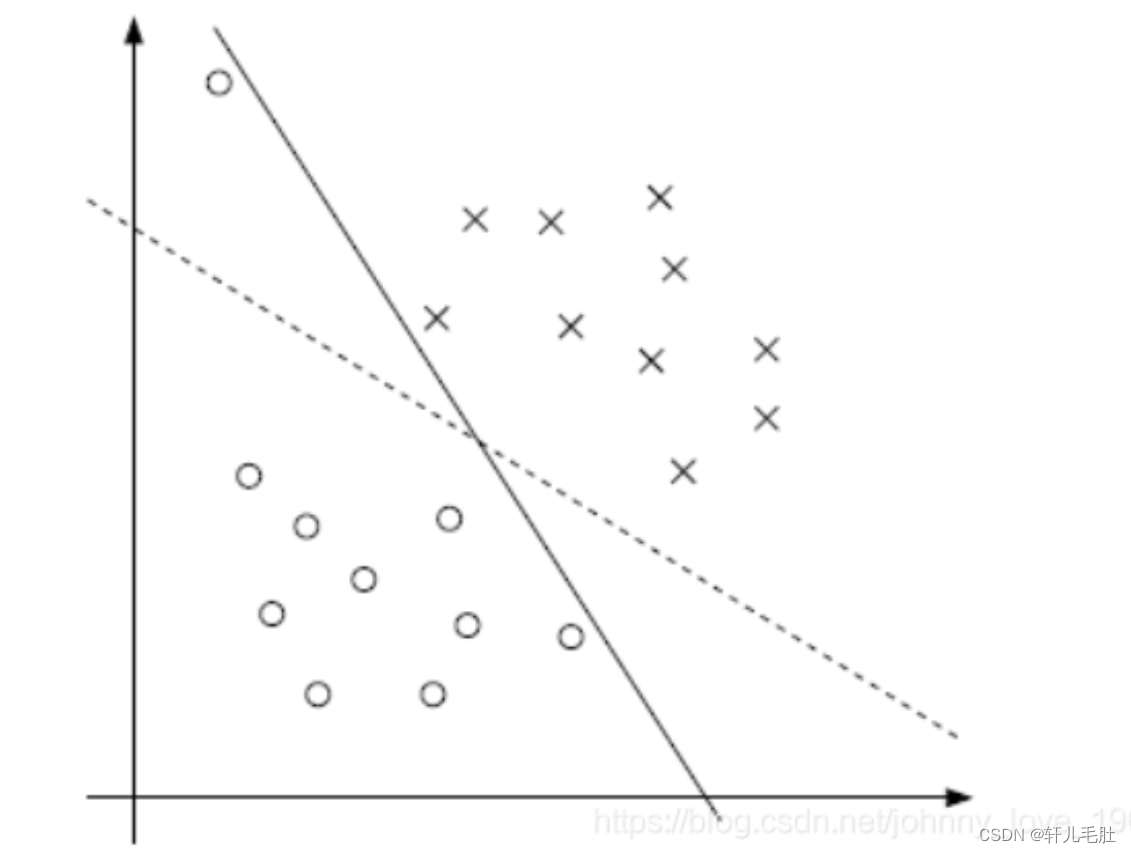
如果按照分割超平面理论,实线应该属于最优的。但是,虚线部分,过渡带比较宽,所以他的泛化能力更好,可以更大可能的避免过拟合。
其次,如果数据根本就不是线性可分(即:线性不可分)的呢?你根本无法通过一条线或面就分的很明白呢?这就是为什么,我们要考虑:线性支持SVM
所谓线性不可分,就是指:一个数据集不可以通过一个线性分类器(直线、平面)来实现分类。这样子的数据集在实际应用中是很常见的,例如:人脸图像、文本文档等。
相关文章:

支持向量机(SVM)
一. 什么是SVM 1. 简介 SVM,曾经是一个特别火爆的概念。它的中文名:支持向量机(Support Vector Machine, 简称SVM)。因为它红极一时,所以关于它的资料特别多,而且杂乱。虽然如此,只要把握住SV…...

Rabbitmq----分布式场景下的应用
服务异步通信-分布式场景下的应用 如果单机模式忘记也可以看看这个快速回顾rabbitmq,在做学习 消息队列在使用过程中,面临着很多实际问题需要思考: 1.消息可靠性 消息从发送,到消费者接收,会经理多个过程: 其中的每一…...
springboot + redis实现签到与统计功能
在很多项目中都会有签到与统计功能,最容易想到的方案是创建一个签到表来记录每个用户的签到记录,比如设计一个mysql数据库表: CREATE TABLE tb_sign id bigint(20) unsigned NOT NULL AUTOINCREMENT COMMENT 主键, user_id bigint(20) unsig…...

Redis | 数据结构(02)SDS
一、键值对数据库是怎么实现的? 在开始讲数据结构之前,先给介绍下 Redis 是怎样实现键值对(key-value)数据库的。 Redis 的键值对中的 key 就是字符串对象,而 value 可以是字符串对象,也可以是集合数据类型…...

Linux C语言开发-D7D8运算符
算术运算符:-*/%,浮点数可以参与除法运算,但不能参与取余运算 a%b:表示取模或取余 关系运算符:<,>,>,<,,! 逻辑运算符:!,&&,|| &&,||逻辑运算符是从左到右,依次运算&#…...
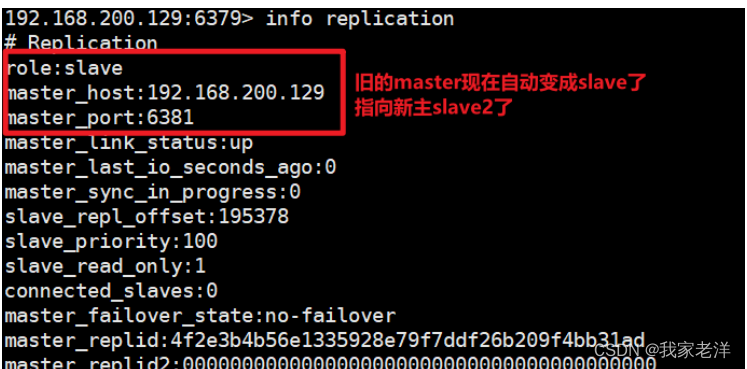
redis 配置主从复制,哨兵模式案例
哨兵(Sentinel)模式 1 . 什么是哨兵模式? 反客为主的自动版,能够自动监控master是否发生故障,如果故障了会根据投票数从slave中挑选一个 作为master,其他的slave会自动转向同步新的master,实现故障自动转义 2 . 原理…...
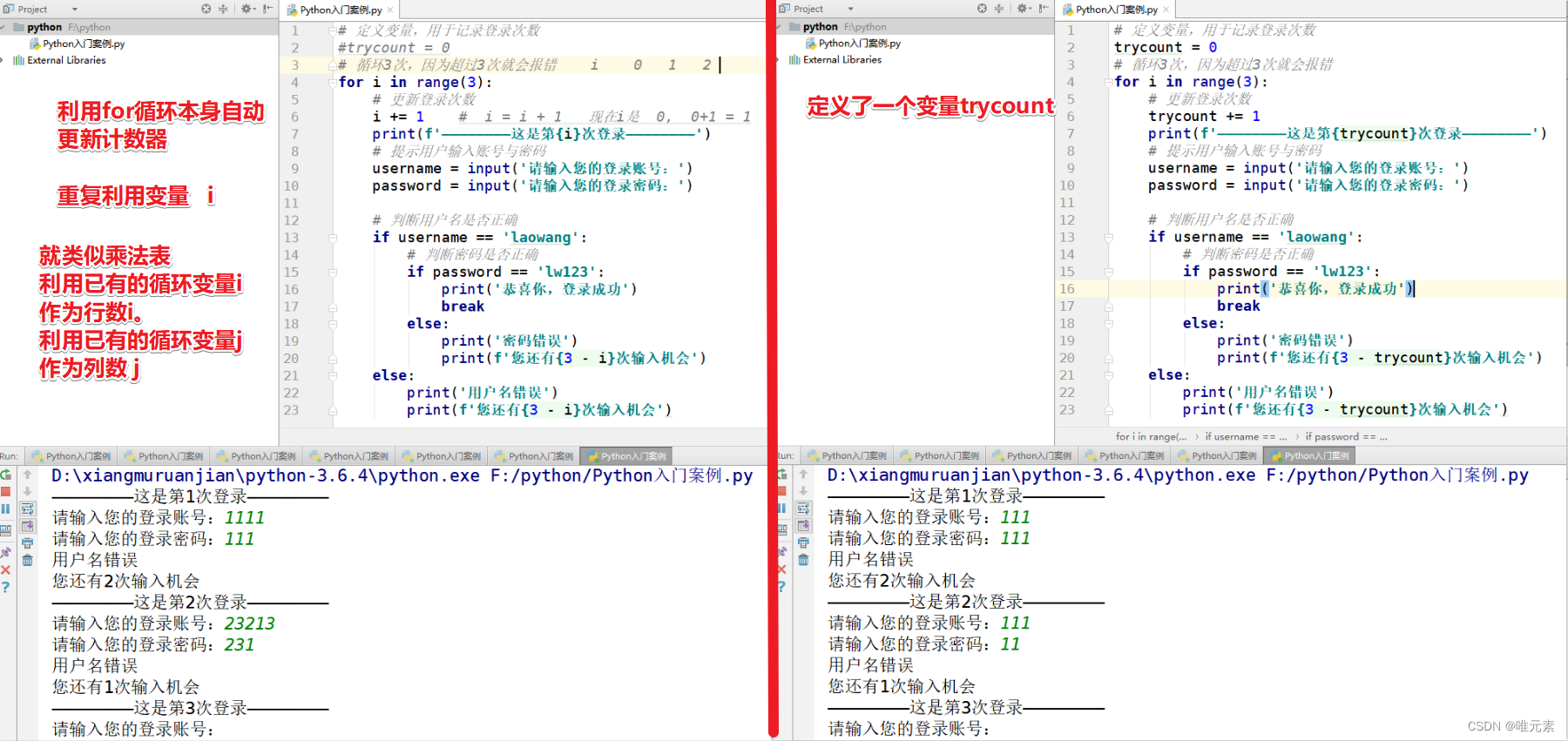
Python---练习:使用for循环实现用户名+密码认证
案例: 用for循环实现用户登录 ① 输入用户名和密码 ② 判断用户名和密码是否正确(usernamelaowang,passwordlw123) ③ 登录仅有三次机会,超过3次会报错 思考: 用户登陆情况有3种: ① 用户名错误(此时…...

react中使用jquery 语法
react中使用jquery 语法 npm install jquery引入 import $ from ‘jquery’ import React from react; import ./css/App.css import { Button } from antd; import $ from jquerylet slider_img [https://cdn.jsdelivr.net/gh/xaoxuu/cdn-wallpaper/abstract/41F215B9-261F…...

服务器中了360后缀勒索病毒怎么解决,勒索病毒解密,数据恢复
近期,网络上的各种病毒都比较猖獗,而其中较为明显的就是360后缀勒索病毒,从这个月开始云天数据恢复中心接到很多企业的求助,企业的服务器遭到了360后缀勒索病毒的攻击,通过给用户的服务器检测与加密病毒的分析…...
使用字节流读取文件中的数据的几种方式
public class FileReader02_ {public static void main(String[] args) {}Testpublic void m1() {String filePath "e:\\hello.txt";FileReader fileReader null;int date0;try {fileReader new FileReader(filePath);//循环读取 使用readwhile ((datefileReader.…...
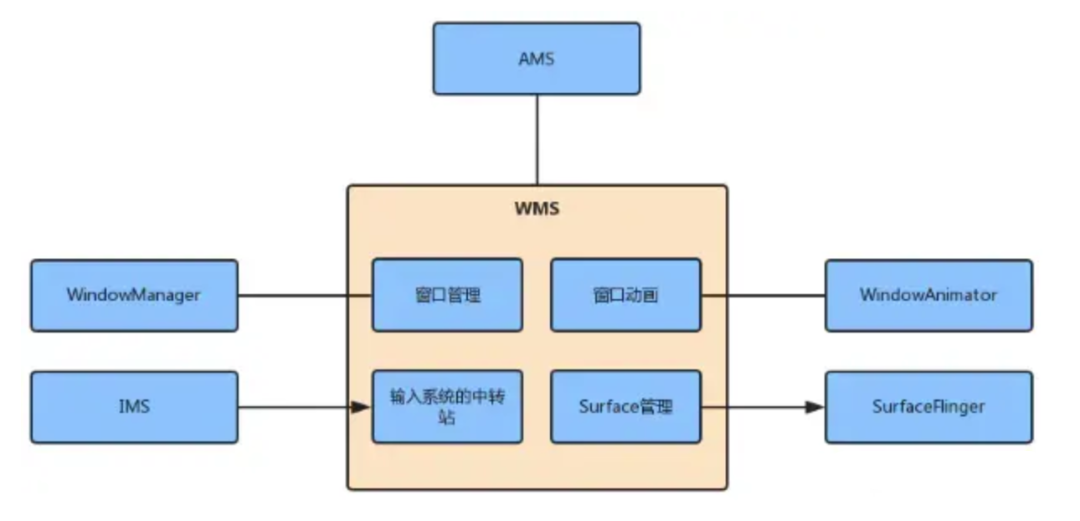
Android WMS——概述(一)
Android 中的 WMS 指的是 Window Manager Service(窗口管理服务)。WMS 是 Android 系统中的核心服务,主要分为四大部分,分别是窗口管理,窗口动画,输入系统中转站和 Surface 管理 。负责管理应用程序窗口的创建、移动、调整大小和显示等操作。 一、功能简介 WMS 的职责可…...
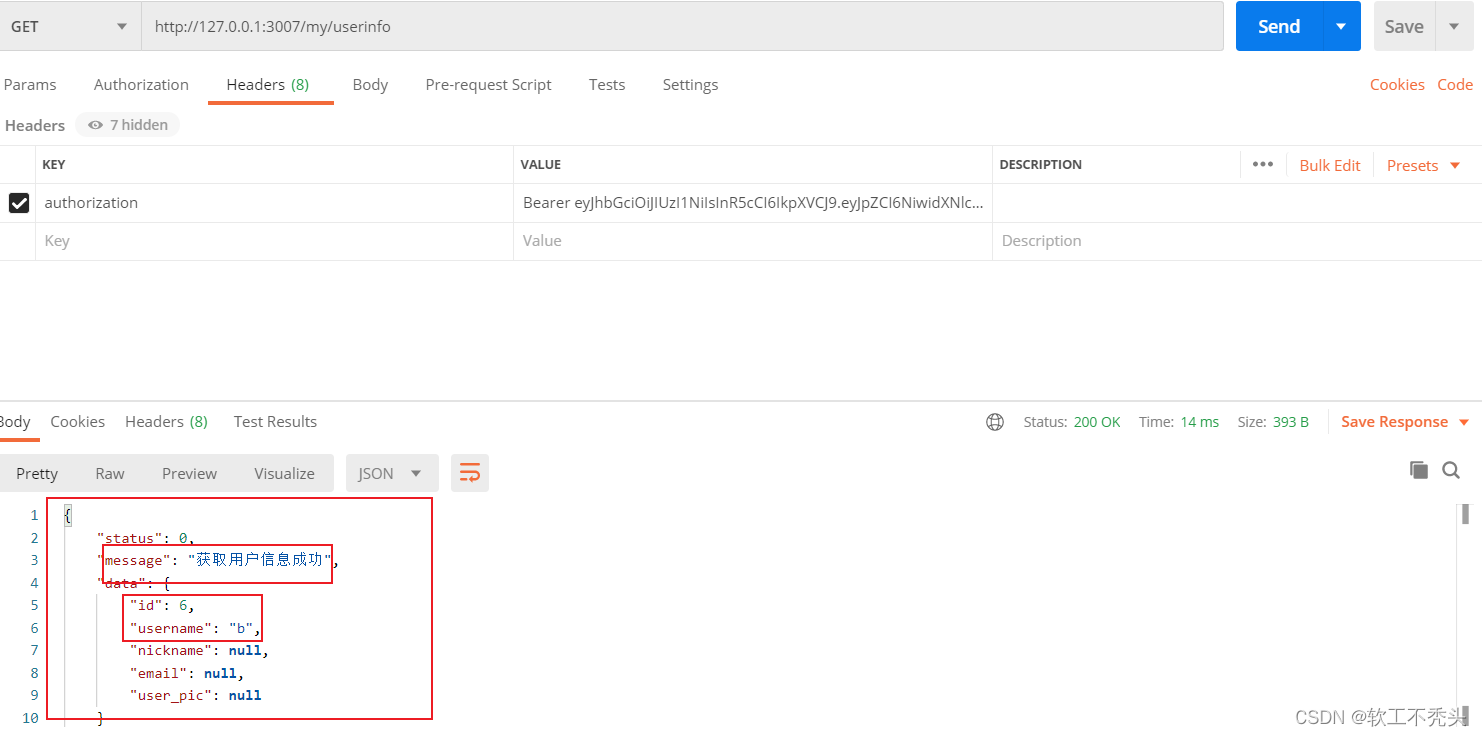
Node编写获取用户信息接口
目录 前言 初始化路由模块 使用postman发送get获取用户信息请求 初始化路由处理函数模块 获取用户基本信息 前言 在前两篇文章中已经介绍了如何编写用户注册接口以及用户登录接口,这篇文章介绍如何获取用户信息,本篇文章建立在Node编写用户登录接口…...

【从0到1设计一个网关】自研网关的设计要点以及架构设计
文章目录 请求的流程架构设计设计要点项目架构流程设计源码地址: 源码地址 请求的流程 一个HTTP请求发送到网关并完成整个生命周期通常包括以下步骤: 客户端请求: 请求始于客户端,客户端通过HTTP请求(例如GET、POST等)发送请求到API网关的入口点。 API网关接收: API…...

论文-分布式-分布式计算|容错-分布式控制下的自稳定系统
参考文献Self-stabilizing systems in spite of distributed control可以把松散耦合的 循环序列过程 间的同步任务,看成是要保持一个这样的不变性:“系统要处于一种合法状态”因此每个进程在运行每一个可能会改变不变性的步骤之前都要先检查一下是可以执…...

C#压缩图片的方法
/// <summary> /// 图片压缩 /// </summary> /// <param name"imagePath">图片文件路径</param> /// <param name"targetFolder">保存文件夹</param> /// <param name"quality">压缩质量</param&g…...

安装 fcitx + 搜狗/谷歌输入法 之后导致 死机,重启后黑屏只有鼠标可以移动
一般的原因就是 : fcitx 导致的问题 方法就是 先卸载搜狗,再卸载fcitx 解决办法: 首先:ctrlaltF6 进入命令行界面,如果进不去就 ctrlaltF2 接下来执行: sudo apt-get remove sogoupinyin sudo apt-get …...

Maven项目转为SpringBoot项目
Maven项目转为SpringBoot项目 前言创建一个maven项目前的软件的一些通用设置Maven仓库的设置其他的设置字符编码编译器注解支持 创建的Maven项目修改为Spring Boot项目修改pom.xml文件修改启动类-Main新建WAR包所需的类 添加核心配置文件 测试的控制器最后整个项目的目录结构
C语言之预处理
目录 前言 宏定义define的用法 文件包含include的用法 条件编译的用法 其他预处理命令 练习题 练习一 练习二 练习三 前言 预处理命令可以改变程序设计环境,提高编程效率,它们并不是C语言本身的组成部分,不能直接对它们进行编译&am…...

css步骤条
html 代码以及样式 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>css步骤条</title><style>.steps {display: flex;justify-content: space-between;padding: 0;margin: 20px 10px;lis…...

[Hive] 常见函数
文章目录 字符串函数数值函数随机函数日期和时间函数字符串转时间 聚合函数数组函数结构体函数数组函数映射函数 map正则处理JSON 字符串函数 CONCAT(string1, string2, …):将多个字符串连接成一个字符串。 LENGTH(string):返回字符串的长度。 LOWER…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
