当前位置： 首页 > news >正文

深度学习与计算机视觉（一）

news 2026/4/6 4:36:20

文章目录

    • 计算机视觉与图像处理的区别
    • 人工神经元
    • 感知机 - 分类任务
    • Sigmoid神经元/对数几率回归
    • 对数损失/交叉熵损失函数
    • 梯度下降法- 极小化对数损失函数
    • 线性神经元/线性回归
      • 均方差损失函数-线性回归常用损失函数
      • 使用梯度下降法训练线性回归模型
      • 线性分类器
        • 多分类器的决策面
      • softmax Regression
      • 训练softmax regression
      • 交叉熵损失
      • 解决参数冗余
      • 训练softmax Classifier
      • 混淆矩阵
      • 合页（铰链）损失

计算机视觉与图像处理的区别

  • 图像处理得到的结果是处理后的图像，图像处理的目的是改善图像的质量

    • 图像增强
    • 图像复原

  • 计算机视觉得到的结果可能是一个符号、一堆数据、一个知识

    • 人脸识别
    • 人脸比对

  • 传统的图像识别的机器学习方法的一般流程包括：

    • 特征提取→数据
    • 数据→机器学习

  • 为什么要提取图像的特征

    • 提取有利于识别的信息，抑制与识别无关的或者对识别有干扰的信息
    • 把不同尺度的图像映射到一个统一的特征空间，便于应用机器学习算法。

  • 机器学习的框架：D数据，A算法，H假设空间，h* H中最好的假设（真实误差最小的假设）
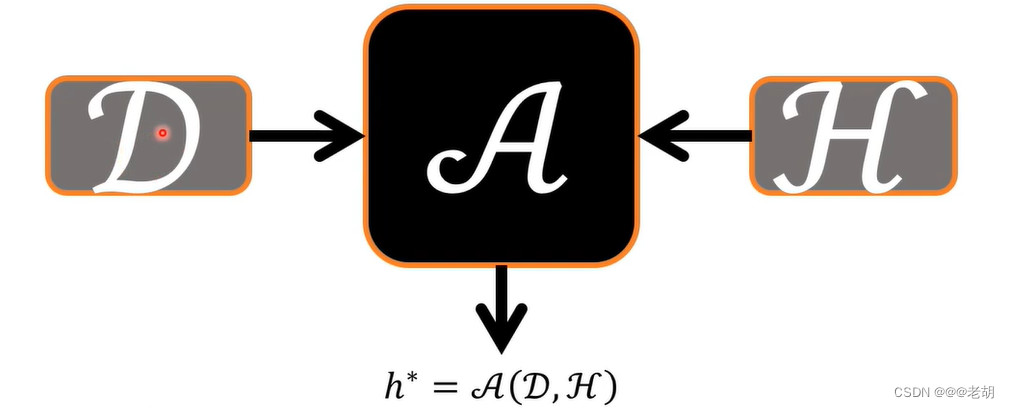
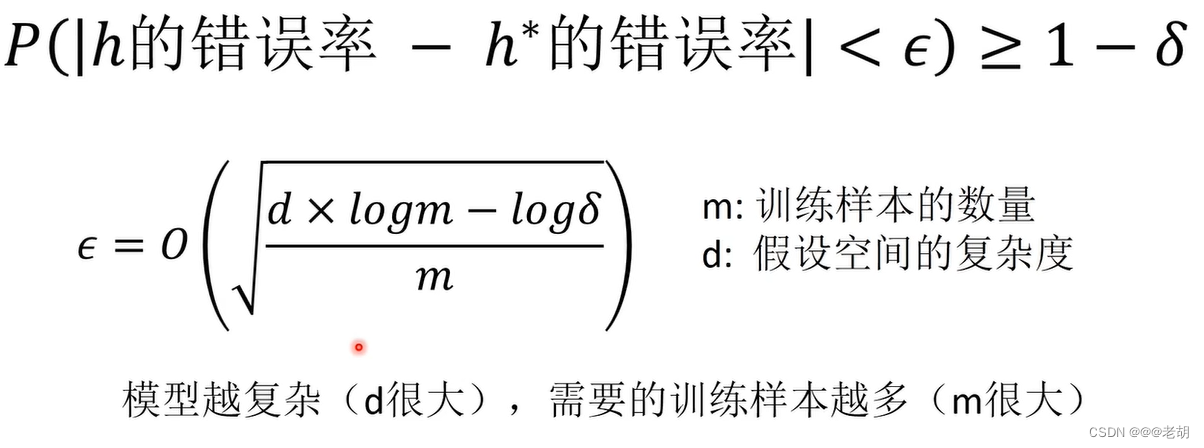
    在这里插入图片描述

  • 概率近似正确
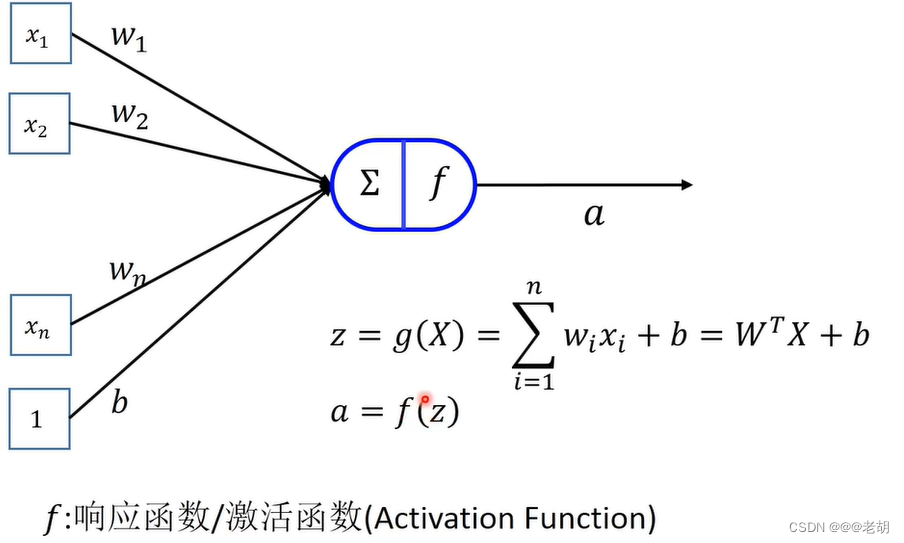
    在这里插入图片描述

人工神经元

在这里插入图片描述

f：响应函数/激活函数一般都是非线性的函数，且一般都单调递增；常用的激活函数包括以下：

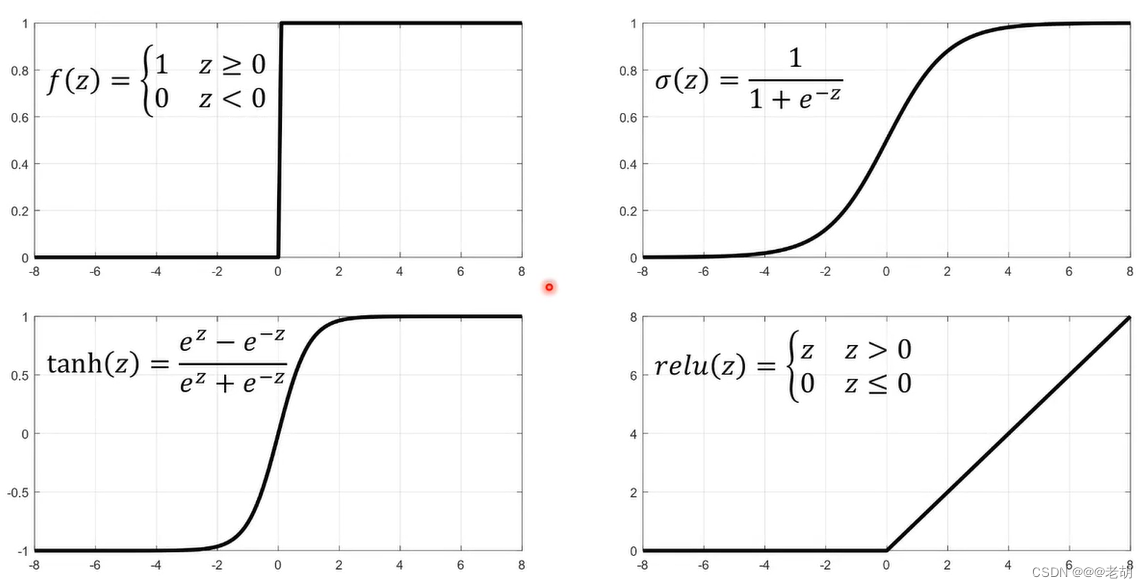
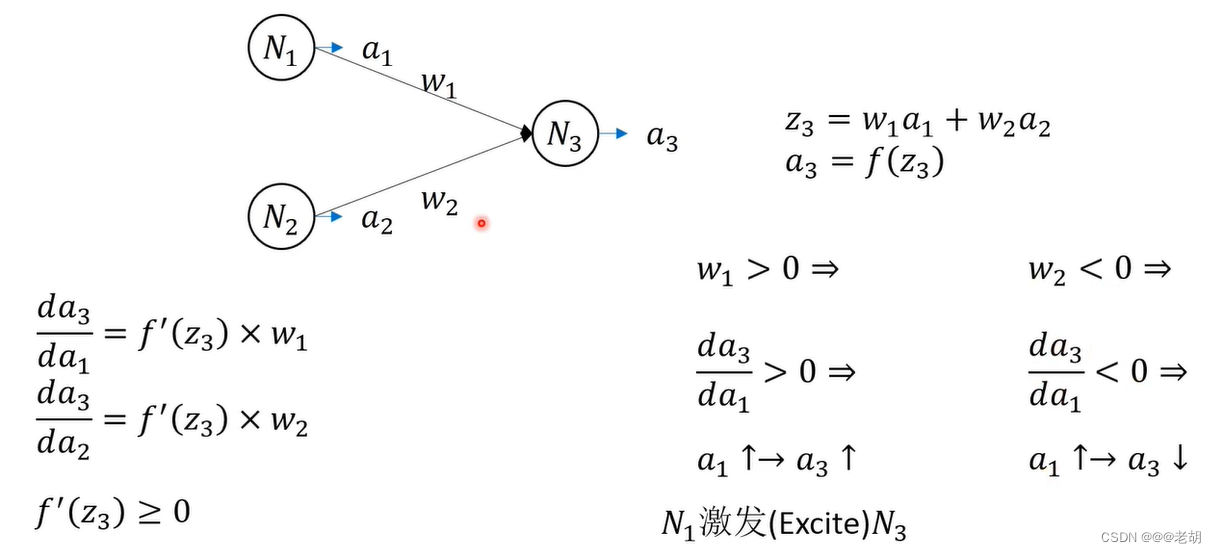
在这里插入图片描述
在这里插入图片描述

因为f是单调递增的函数，，如果 w>0，则，说明前一个神经元对后一个神经元有激活的作用；如果w<0 ，说明前一个神经元对后一个神经元有抑制作用。

感知机 - 分类任务

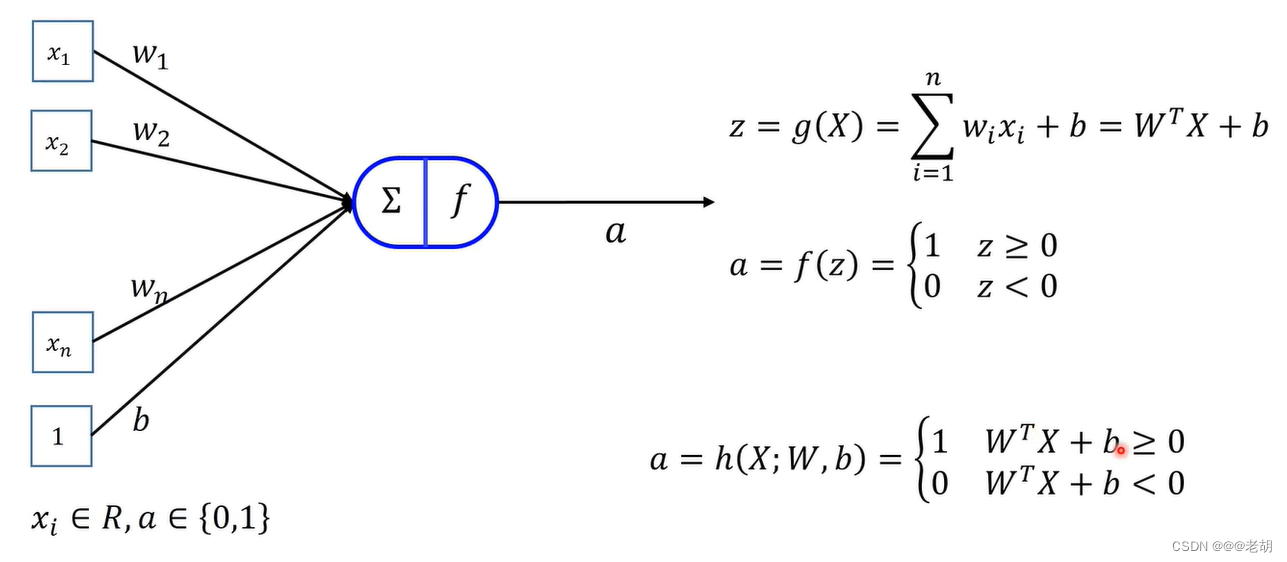
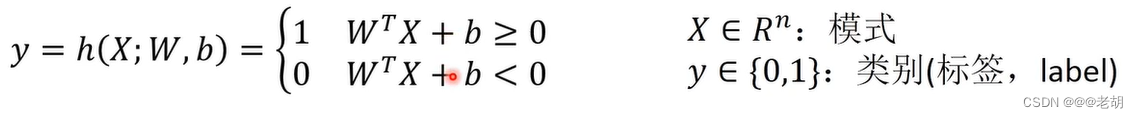
在这里插入图片描述
在这里插入图片描述

  • 感知机算法在线性可分的情况下，一定可以收敛，也就是一定可以找到一个能正确分类所有样本的分类函数
  • 但是同一个样本集，有可能会得到不同的解
    • 不同的初始值，不同的样本处理次序产生的结果不同
    • 不能得到全局最优的解
  • 线性不可分的时候，算法会失败

感知机的算法

在这里插入图片描述

损失函数：不能处处可导

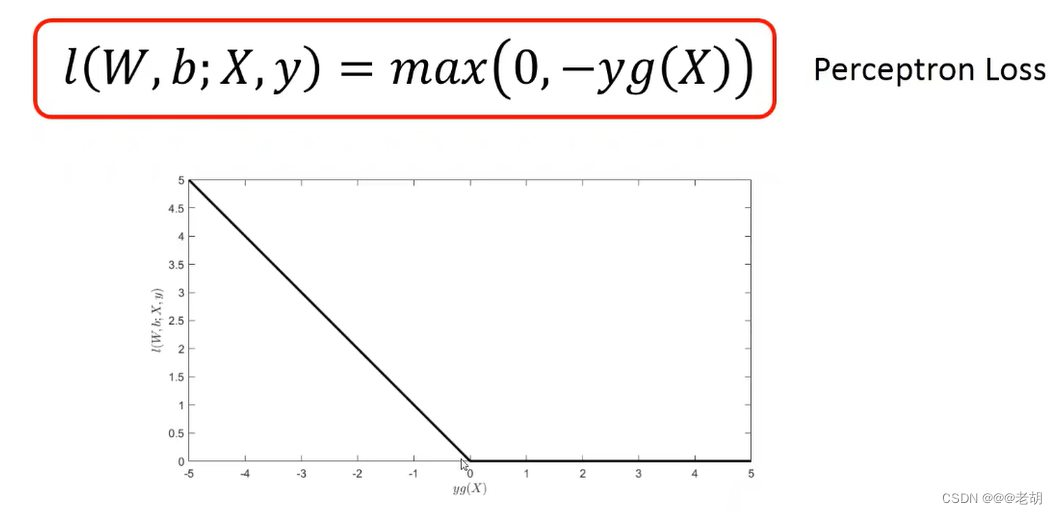
在这里插入图片描述
在这里插入图片描述

解决方法：次梯度

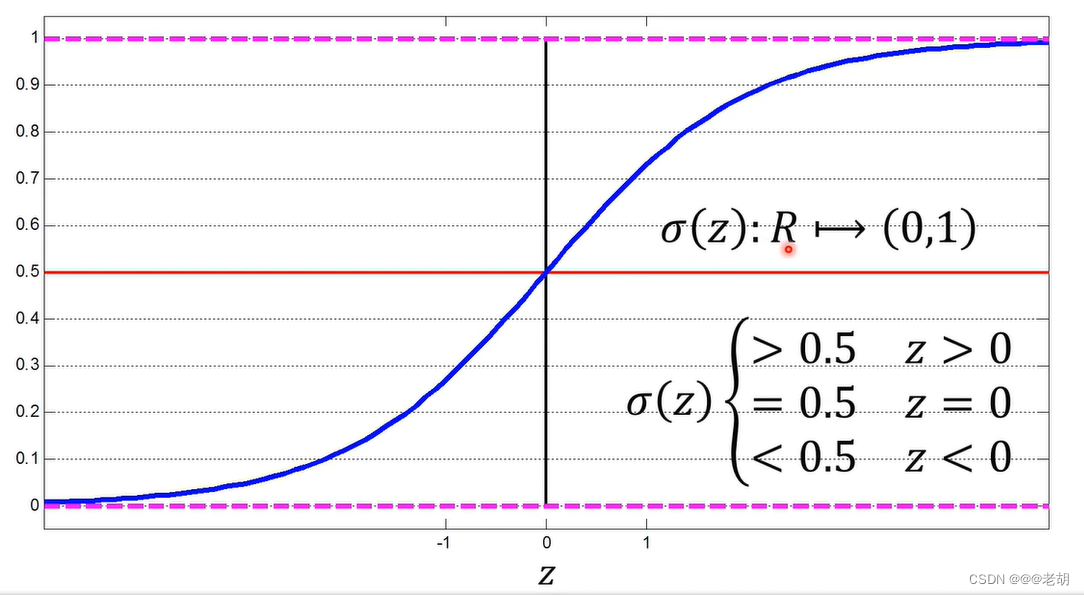
Sigmoid神经元/对数几率回归

只有激活函数的不同，sigmoid处处连续可导，输出的是对数几率
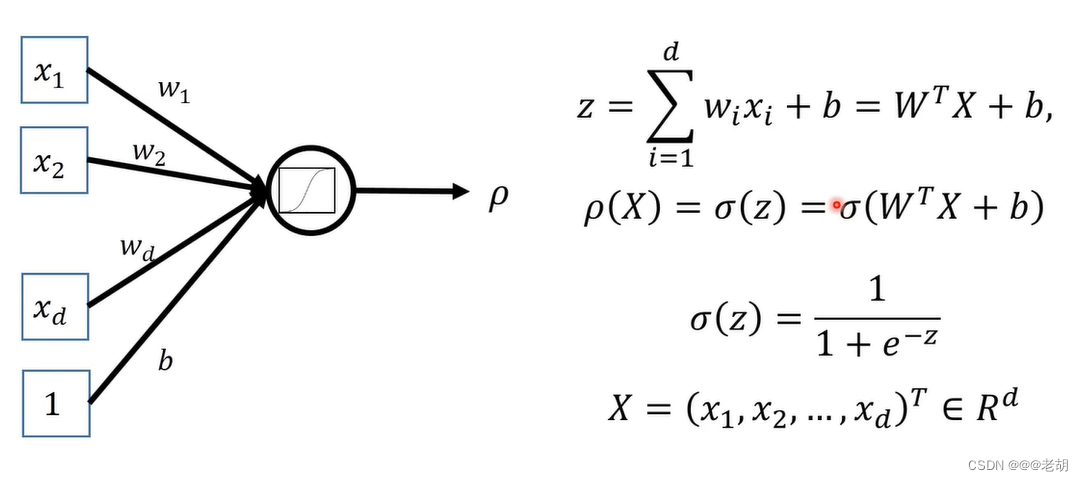
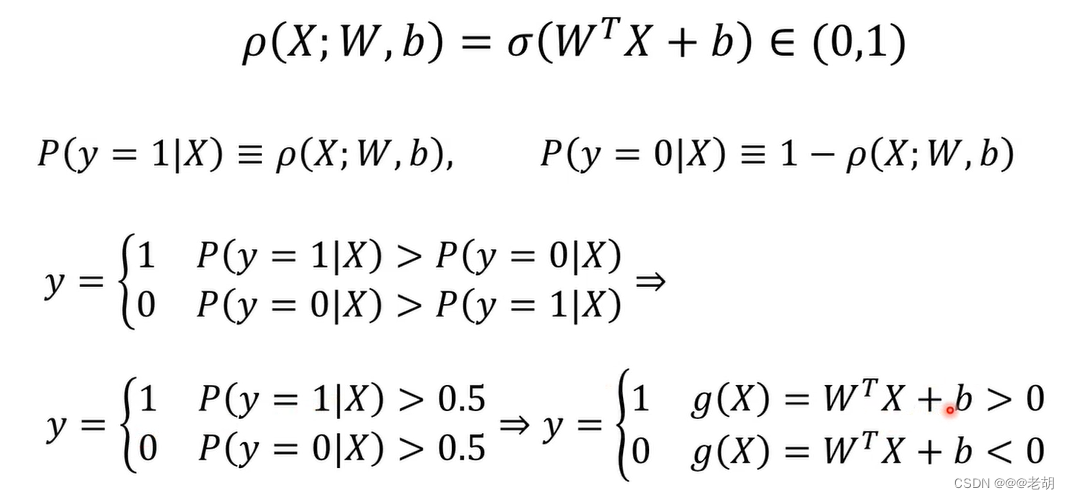
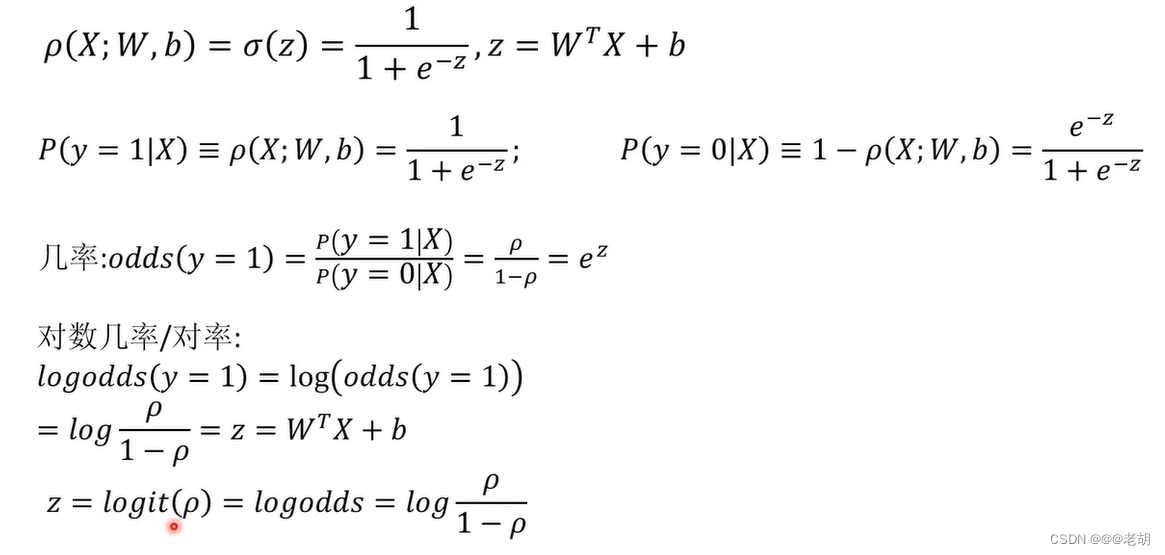
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

对数损失/交叉熵损失函数

损失函数通过比较模型对样本X的预测结果与样本的真实类别y之间的差异，计算损失，差异越大，损失越大，差异越小，损失越小。

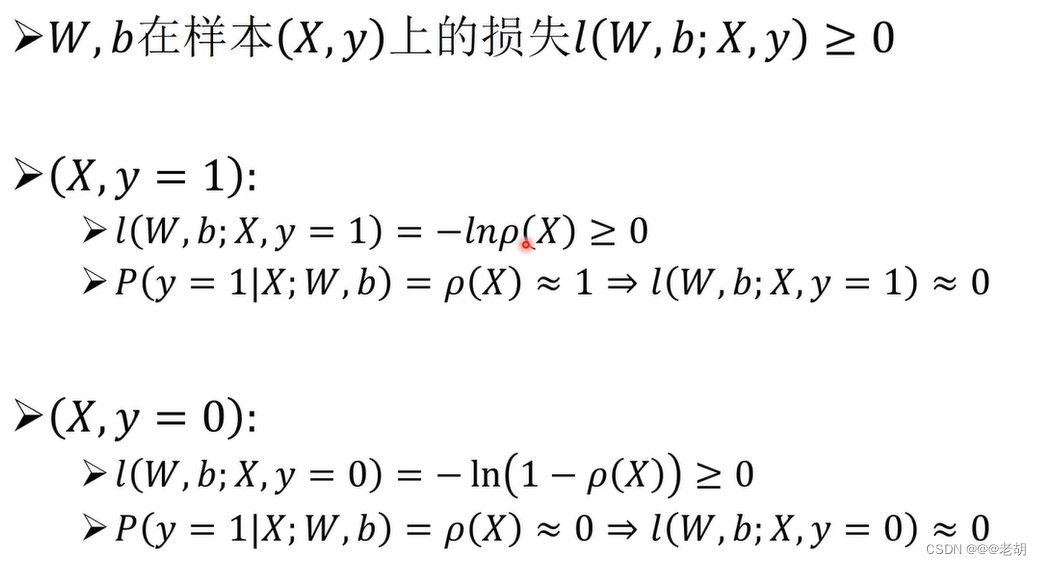
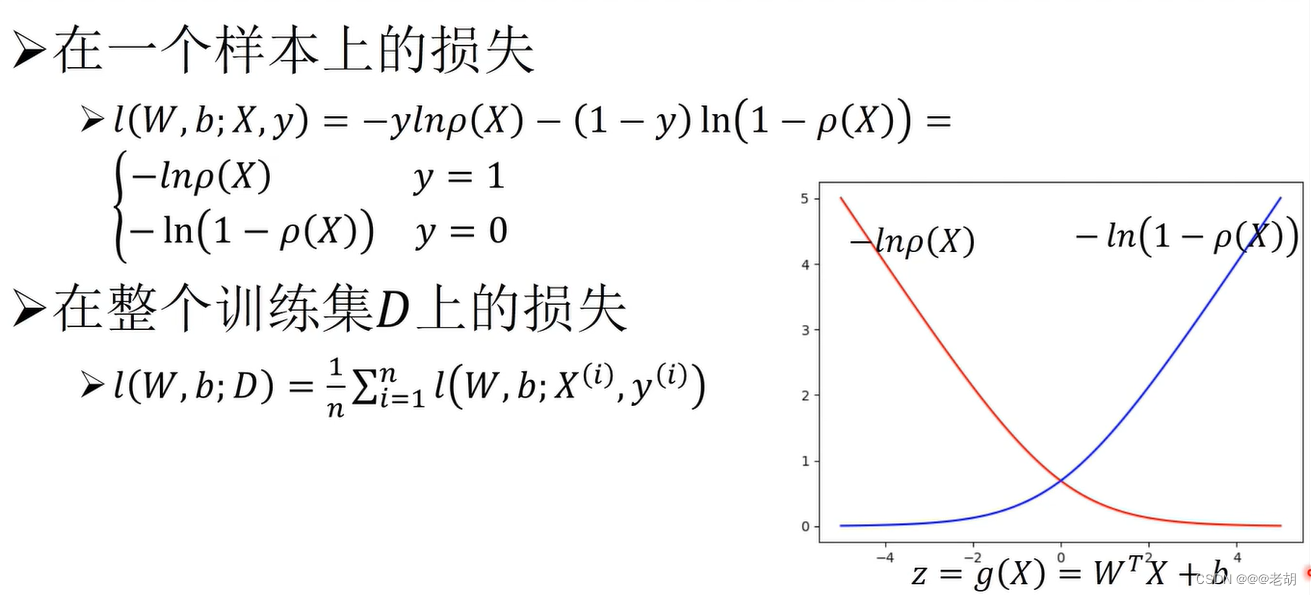
在这里插入图片描述
在这里插入图片描述

梯度下降法- 极小化对数损失函数

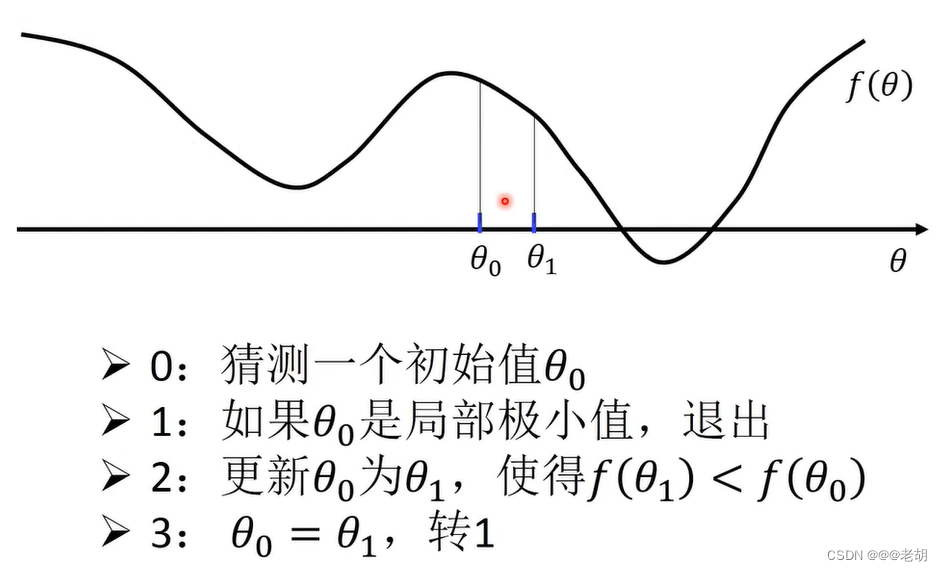
在这里插入图片描述

线性神经元/线性回归

神经元有两个部分组成：收集信号的过程和激活的过程，收集信号如果是使用线性过程（累加）就是线性神经元。至于收集到的信号能不能激活下一个神经元，要看激活函数的过程，这个过程一般不是线性的。

均方差损失函数-线性回归常用损失函数

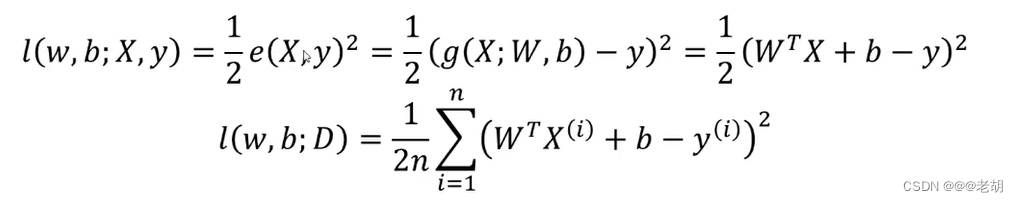
在这里插入图片描述

使用梯度下降法训练线性回归模型

是对w，b进行更新

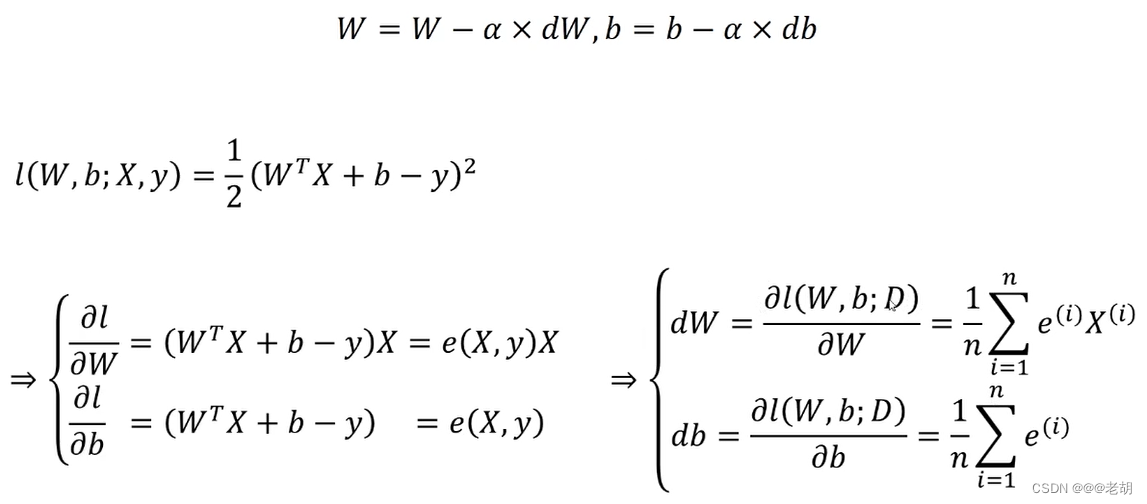
在这里插入图片描述
一元导数与微分的关系： d f / d x = f ′ 一元导数与微分的关系：df/dx=f' 一元导数与微分的关系：df/dx=f′
全微分： d F = ( α F / α x ) d x + ( α F / α y ) d y 全微分：dF=(αF/αx) dx+(αF/αy) dy 全微分：dF=(αF/αx)dx+(αF/αy)dy
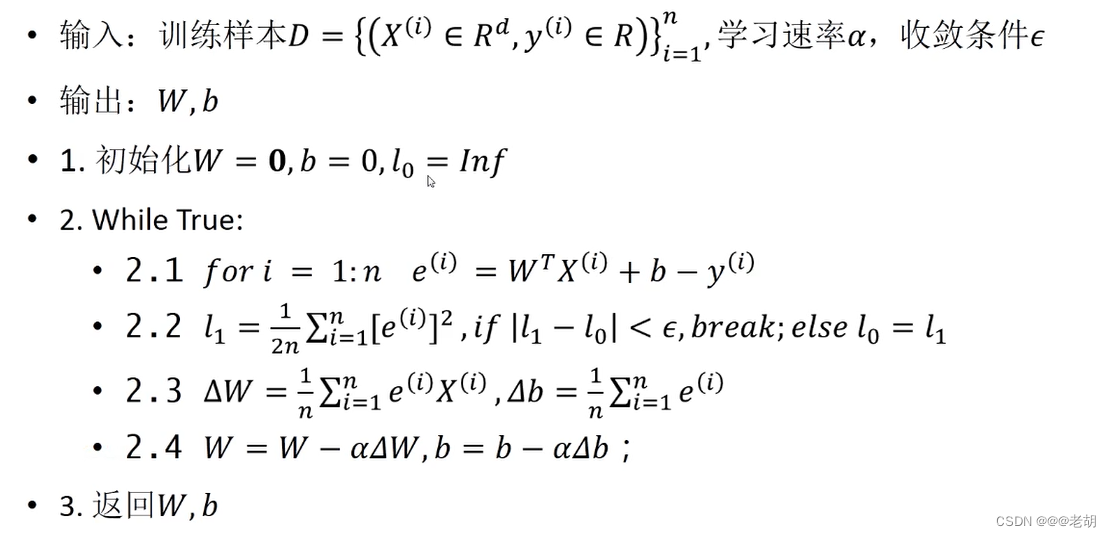
在这里插入图片描述

线性分类器

α ∗ β = ∣ α ∣ ∗ ∣ β ∣ c o s < α ， β > （ α ， β 为向量），其中 ∣ β ∣ c o s < α ， β > 称为 β 在 α 上的投影 α*β=|α|*|β|cos<α，β>（α，β为向量），其中|β|cos<α，β>称为β在α上的投影 α∗β=∣α∣∗∣β∣cos<α，β>（α，β为向量），其中∣β∣cos<α，β>称为β在α上的投影
在这里插入图片描述

多分类器的决策面

决策面是可以把各种分类分开的一个面，在三级分类中，决策面应该在超平面的角平分线处划分
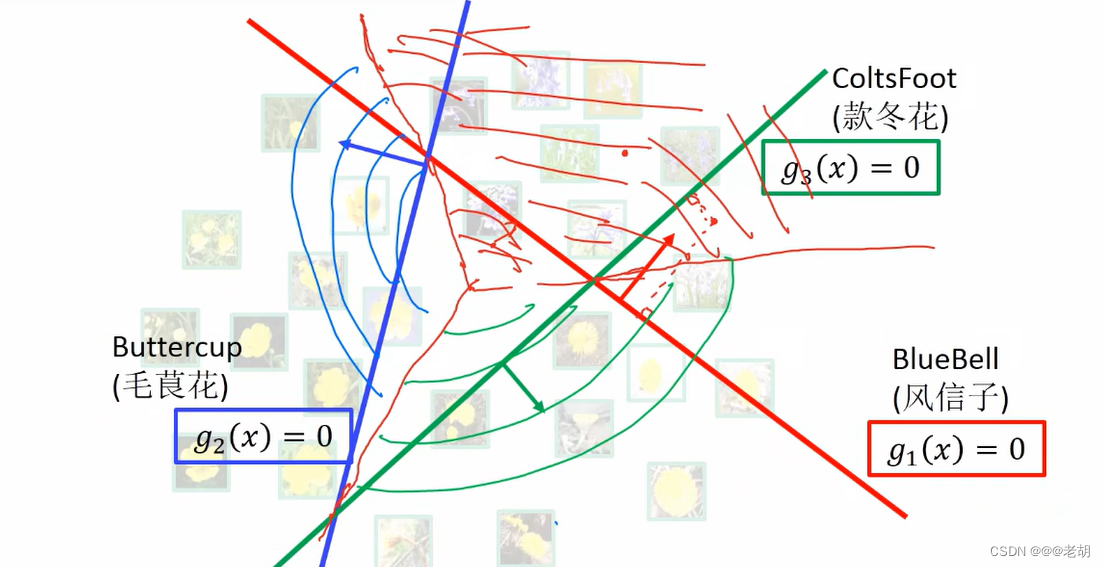
在这里插入图片描述

softmax Regression

在这里插入图片描述

  • 这种argmax会把打分最高的结果设为1，其他的结果设为0；但是这种投影的坏处在于只看得到分类，看不到分类的置信为多少，所以引入了softmax Regression（ e z 变成正数，正数加和为分母，求概率 e^z变成正数，正数加和为分母，求概率 ez变成正数，正数加和为分母，求概率）

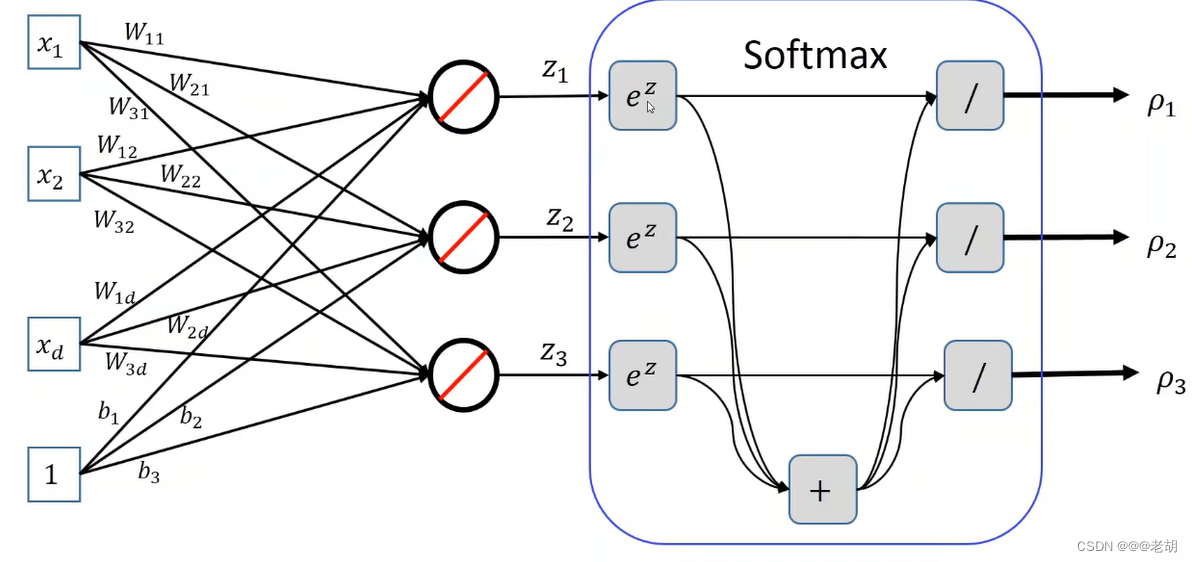
在这里插入图片描述
在这里插入图片描述

softmax的决策规则就是：寻找概率最大的作为分类的输出，又因为e函数是单调递增的，所以只要z最大，则概率就会最大。

训练softmax regression

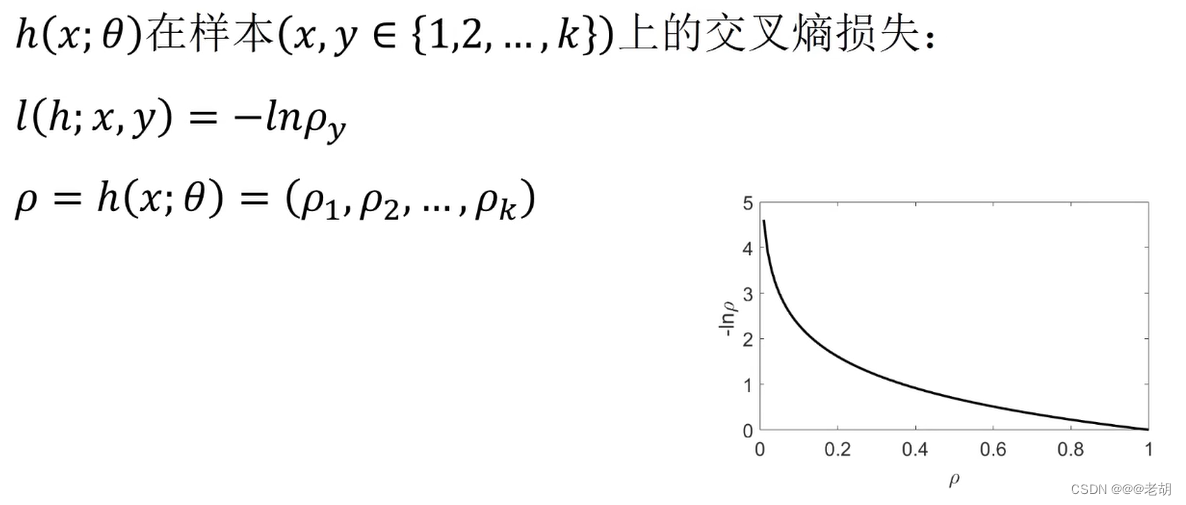
在这里插入图片描述

这里要特别注意，这里计算损失函数的那个概率，是真实样本所对应的概率，不是预测值的那个概率

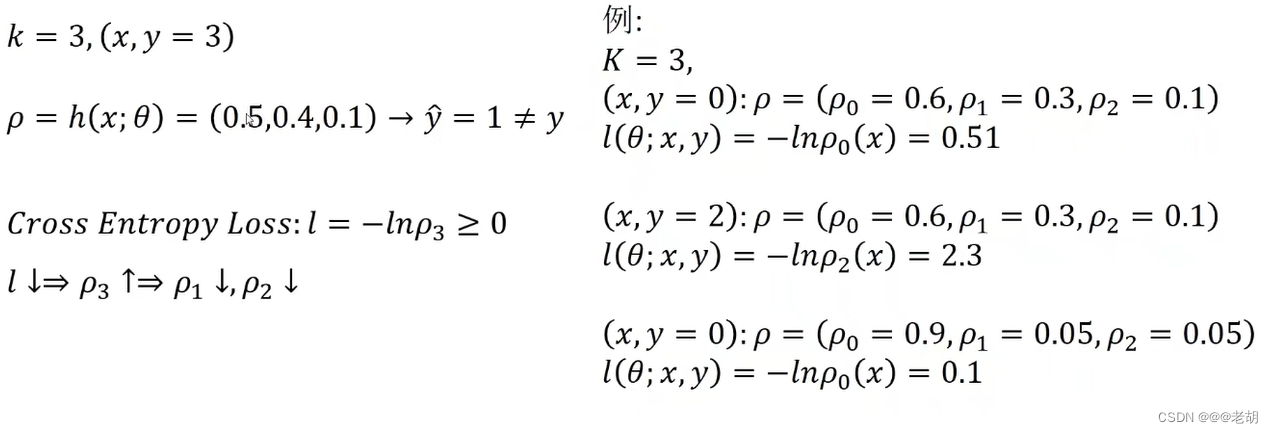
在这里插入图片描述

训练过程

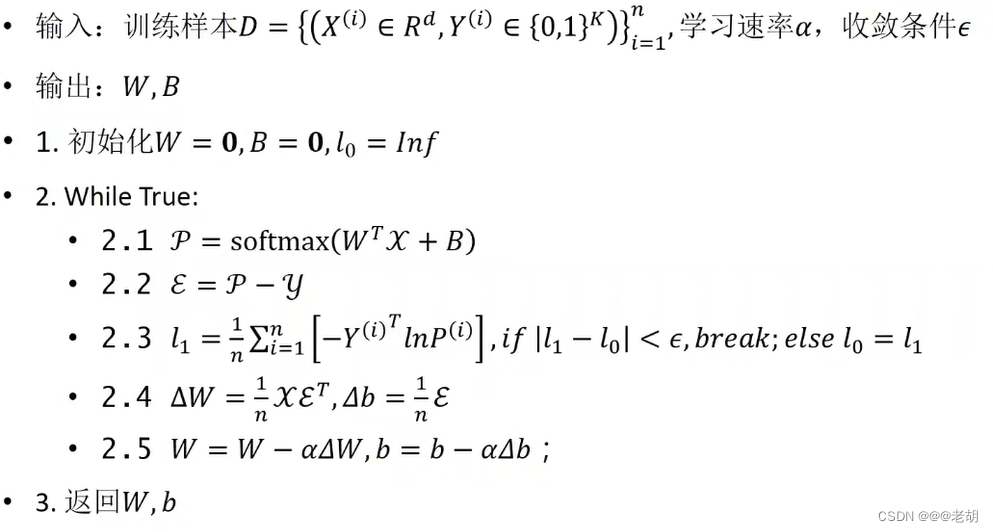
在这里插入图片描述

交叉熵损失

在这里插入图片描述
在这里插入图片描述

解决参数冗余

可以使用一个正则化项：选择损失函数小且Ω也小的

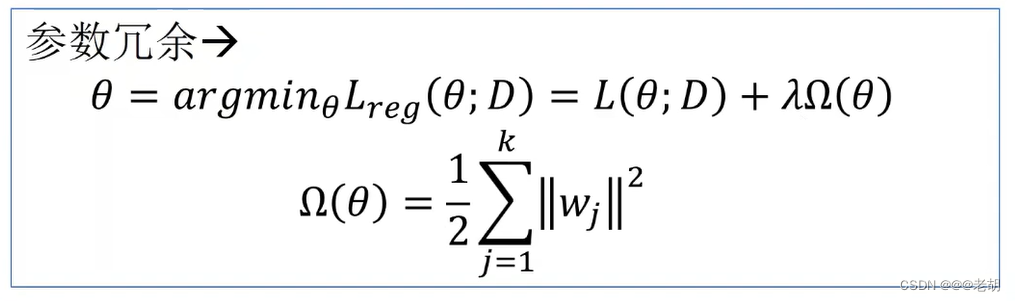
在这里插入图片描述

训练softmax Classifier

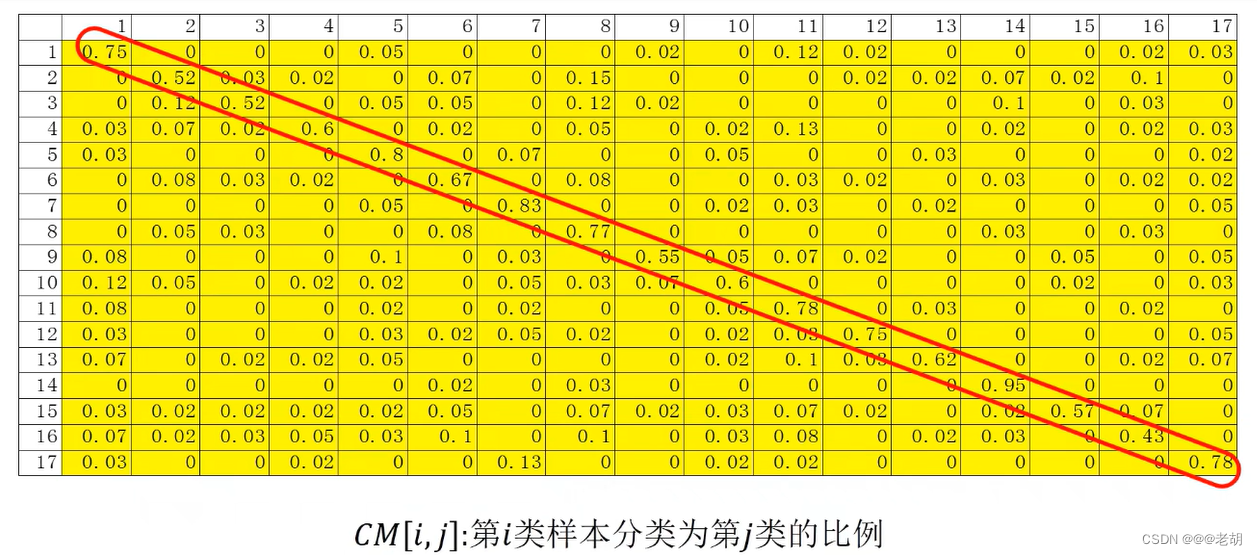
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

混淆矩阵

在这里插入图片描述

对角线上的表示第k个类别的精度，混淆矩阵可以清晰的看到哪一个类别的分类情况较好（精度高），哪一个类别的分类情况不好（精度第），以及具体的分类情况是什么

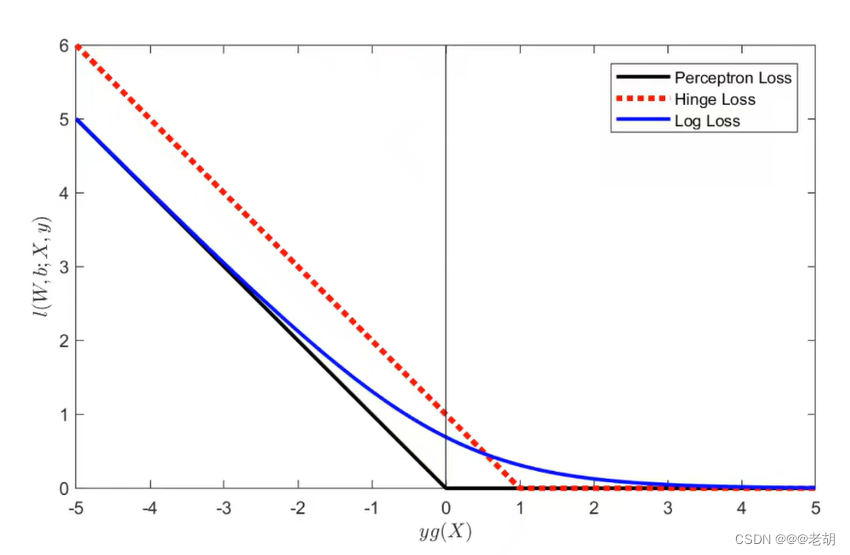
合页（铰链）损失

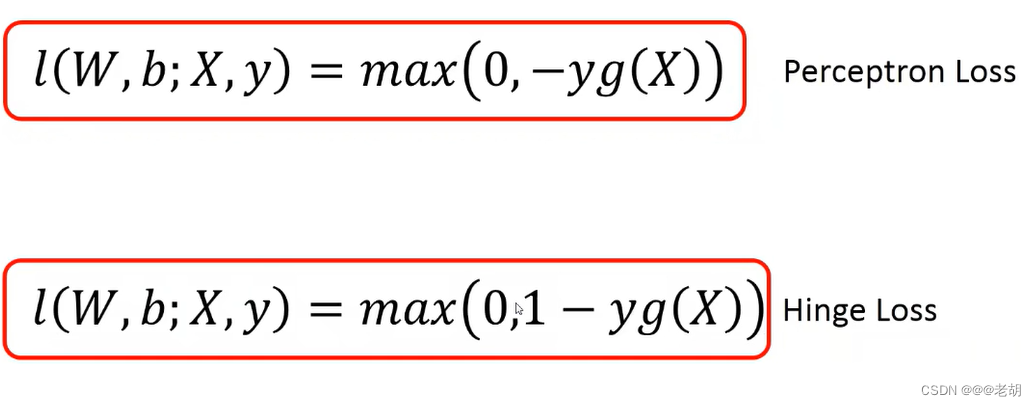
在这里插入图片描述
在这里插入图片描述

相关文章：

深度学习与计算机视觉（一）

文章目录 计算机视觉与图像处理的区别人工神经元感知机 - 分类任务Sigmoid神经元/对数几率回归对数损失/交叉熵损失函数梯度下降法- 极小化对数损失函数线性神经元/线性回归均方差损失函数-线性回归常用损失函数使用梯度下降法训练线性回归模型线性分类器多分类器的决策面 soft…...

编程日记 2023/10/27 1:33:17

【vector题解】杨辉三角 | 删除有序数组中的重复项 | 只出现一次的数字Ⅱ

杨辉三角 力扣&#xff08;LeetCode&#xff09;官网 - 全球极客挚爱的技术成长平台 给定一个非负整数 numRows&#xff0c;生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中&#xff0c;每个数是它左上方和右上方的数的和。 示例 1: 输入: numRows 5 输出: [[1],[1,1…...

编程日记 2023/10/27 1:32:17

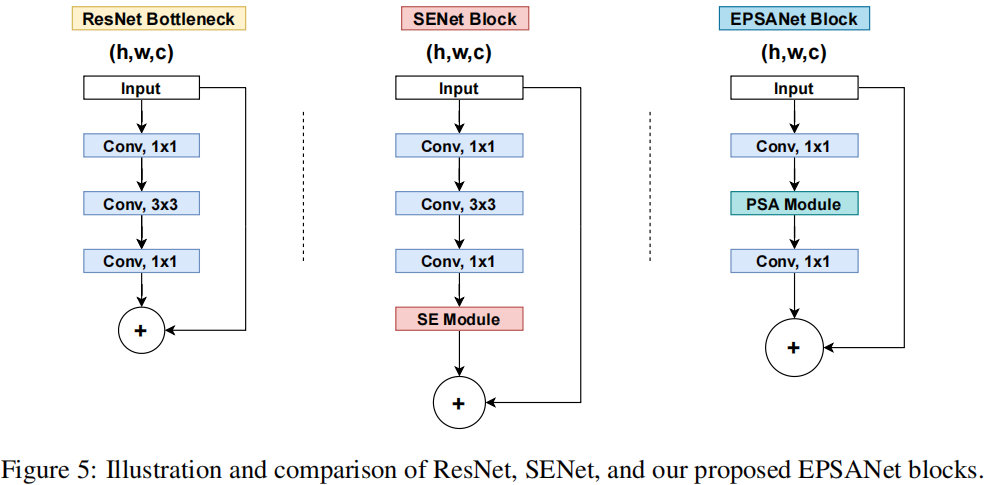
金字塔切分注意力模块PSA学习笔记 （附代码）

已有研究表明&#xff1a;将注意力模块嵌入到现有CNN中可以带来显著的性能提升。比如&#xff0c;SENet、BAM、CBAM、ECANet、GCNet、FcaNet等注意力机制均带来了可观的性能提升。但是&#xff0c;目前仍然存在两个具有挑战性的问题需要解决。一是如何有效地获取和利用不同尺度…...

编程日记 2023/10/27 1:30:14

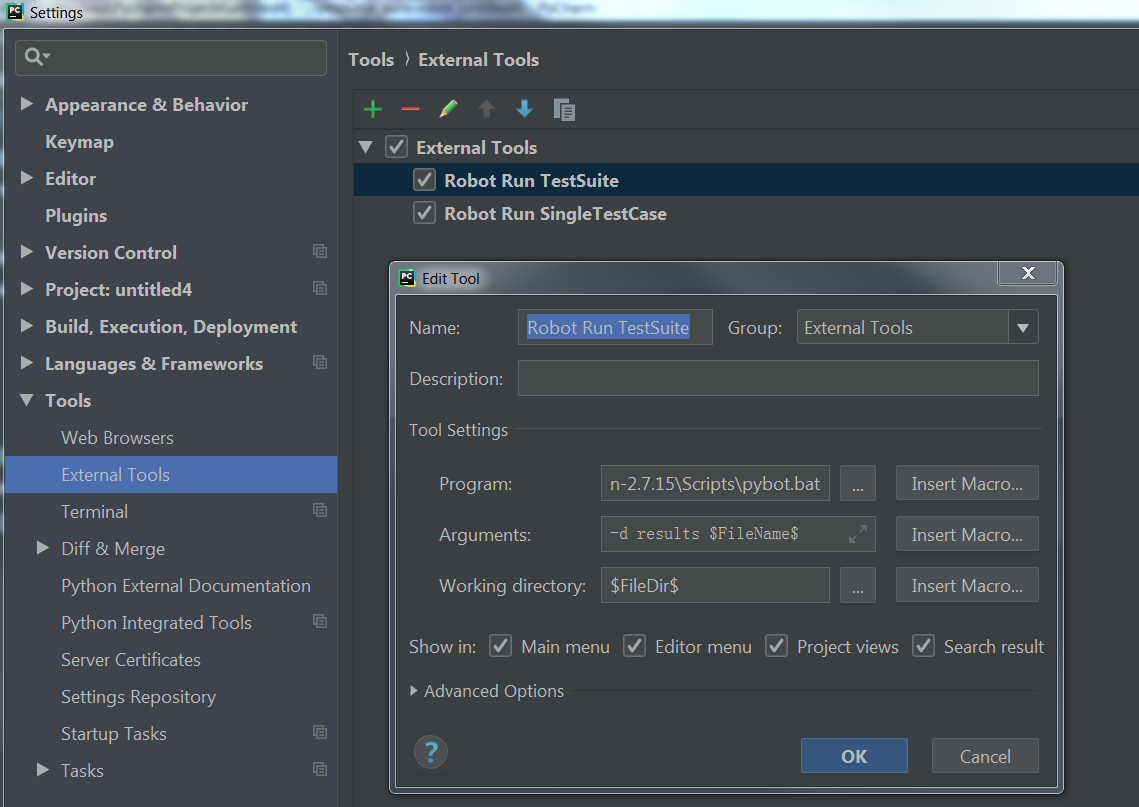
Jenkins自动化测试

学习 Jenkins 自动化测试的系列文章 Robot Framework 概念Robot Framework 安装Pycharm Robot Framework 环境搭建Robot Framework 介绍Jenkins 自动化测试 1. Robot Framework 概念 Robot Framework是一个基于Python的&#xff0c;可扩展的关键字驱动的自动化测试框架。 它…...

编程日记 2023/10/27 1:29:11

python 字典dict和列表list的读取速度问题, range合并

嗨喽&#xff0c;大家好呀~这里是爱看美女的茜茜呐 python 字典和列表的读取速度问题 最近在进行基因组数据处理的时候&#xff0c;需要读取较大数据&#xff08;2.7G&#xff09;存入字典中&#xff0c; 然后对被处理数据进行字典key值的匹配&#xff0c;在被处理文件中每次…...

编程日记 2023/10/27 1:28:08

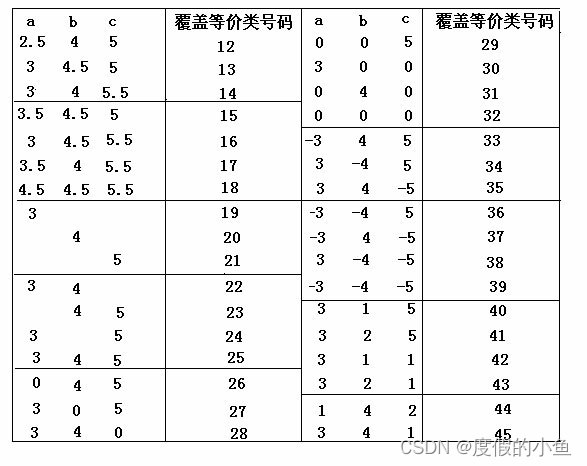
测试用例的设计方法（全）：等价类划分方法

一.方法简介 1.定义 是把所有可能的输入数据,即程序的输入域划分成若干部分&#xff08;子集&#xff09;,然后从每一个子集中选取少数具有代表性的数据作为测试用例。该方法是一种重要的,常用的黑盒测试用例设计方法。 2.划分等价类&#xff1a; 等价类是指某个输入域的…...

编程日记 2023/10/27 1:27:07

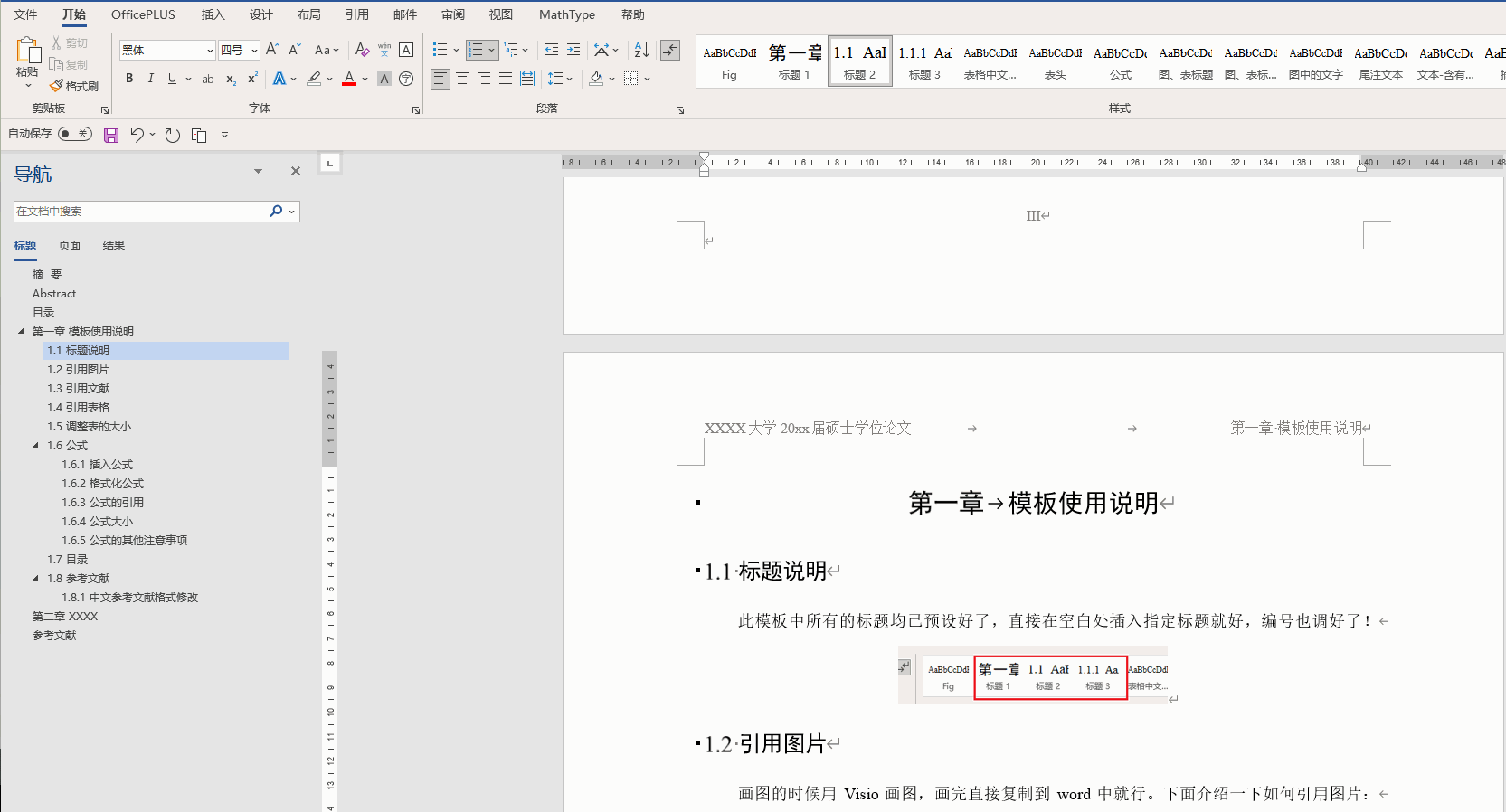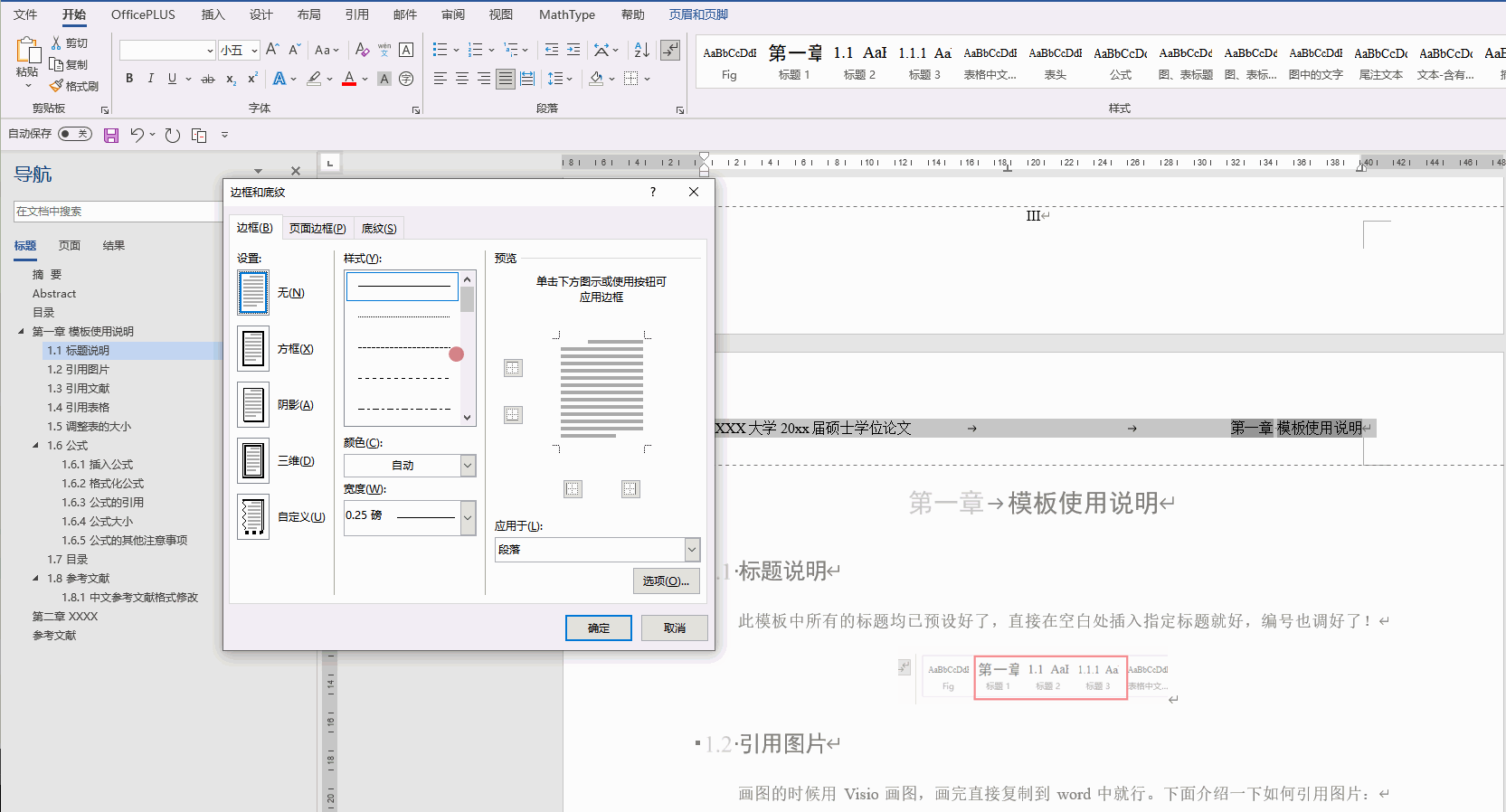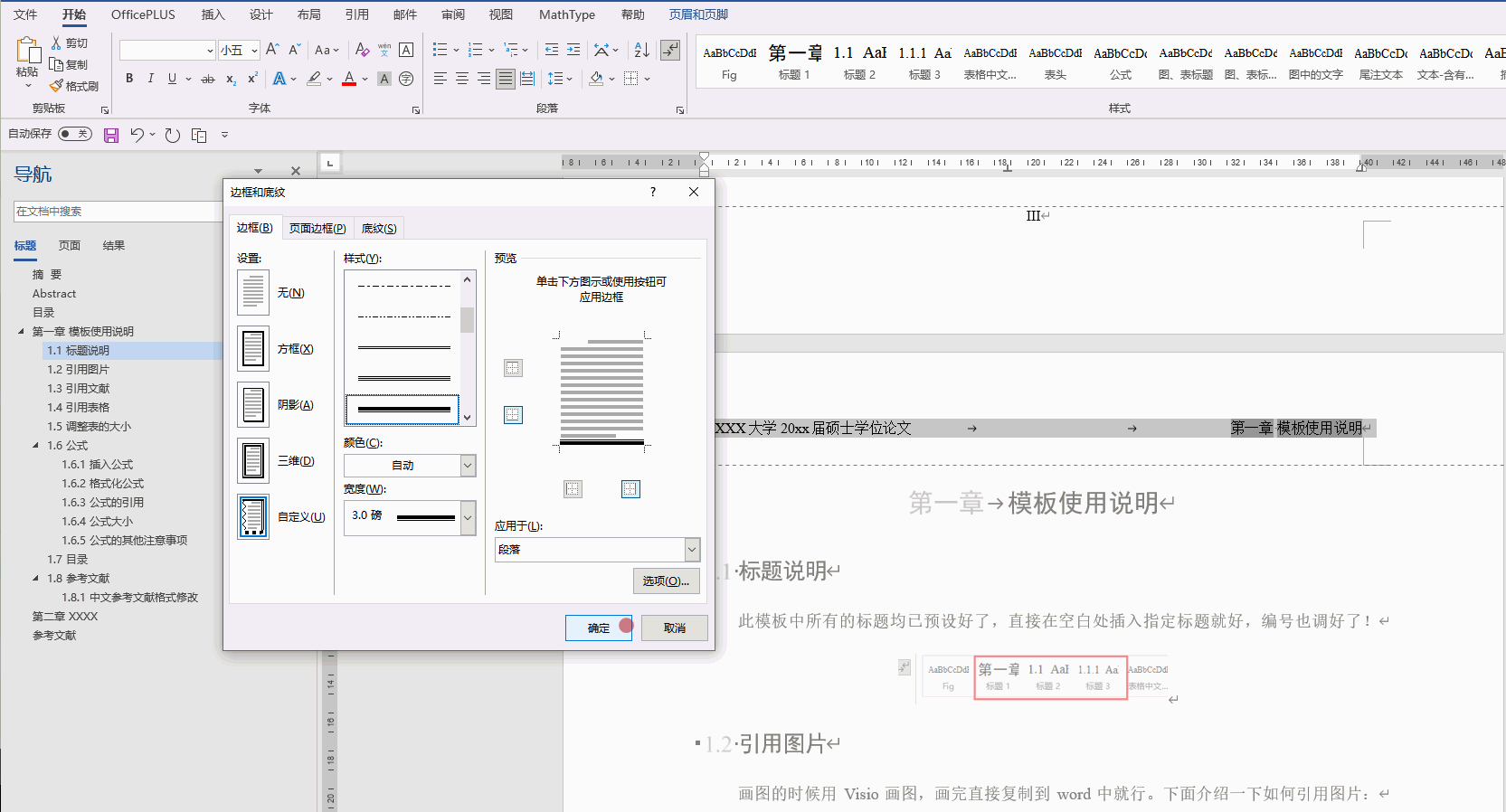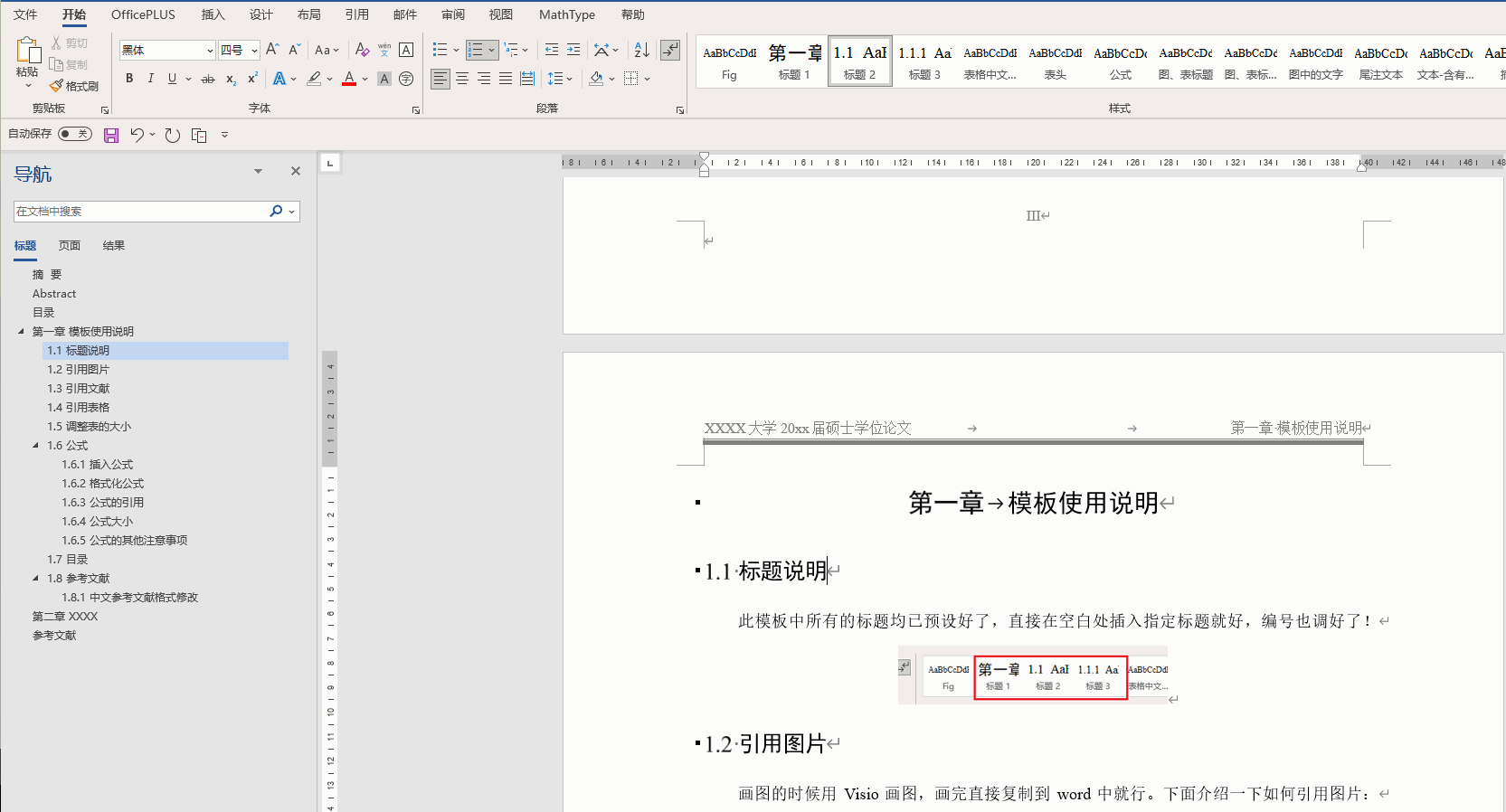
Office技巧（持续更新）（Word、Excel、PPT、PowerPoint、连续引用、标题、模板、论文）

1. Word 1.1 标题设置为多级列表 选住一级标题&#xff0c;之后进行“定义新的多级列表” 1.2 图片和表的题注自动排序 正常插入题注后就可以了。如果一级标题是 “汉字序号”&#xff0c;那么需要对题注进行修改&#xff1a; 从原来的 图 { STYLEREF 1 \s }-{ SEQ 图 \* A…...

编程日记 2023/10/27 1:26:05

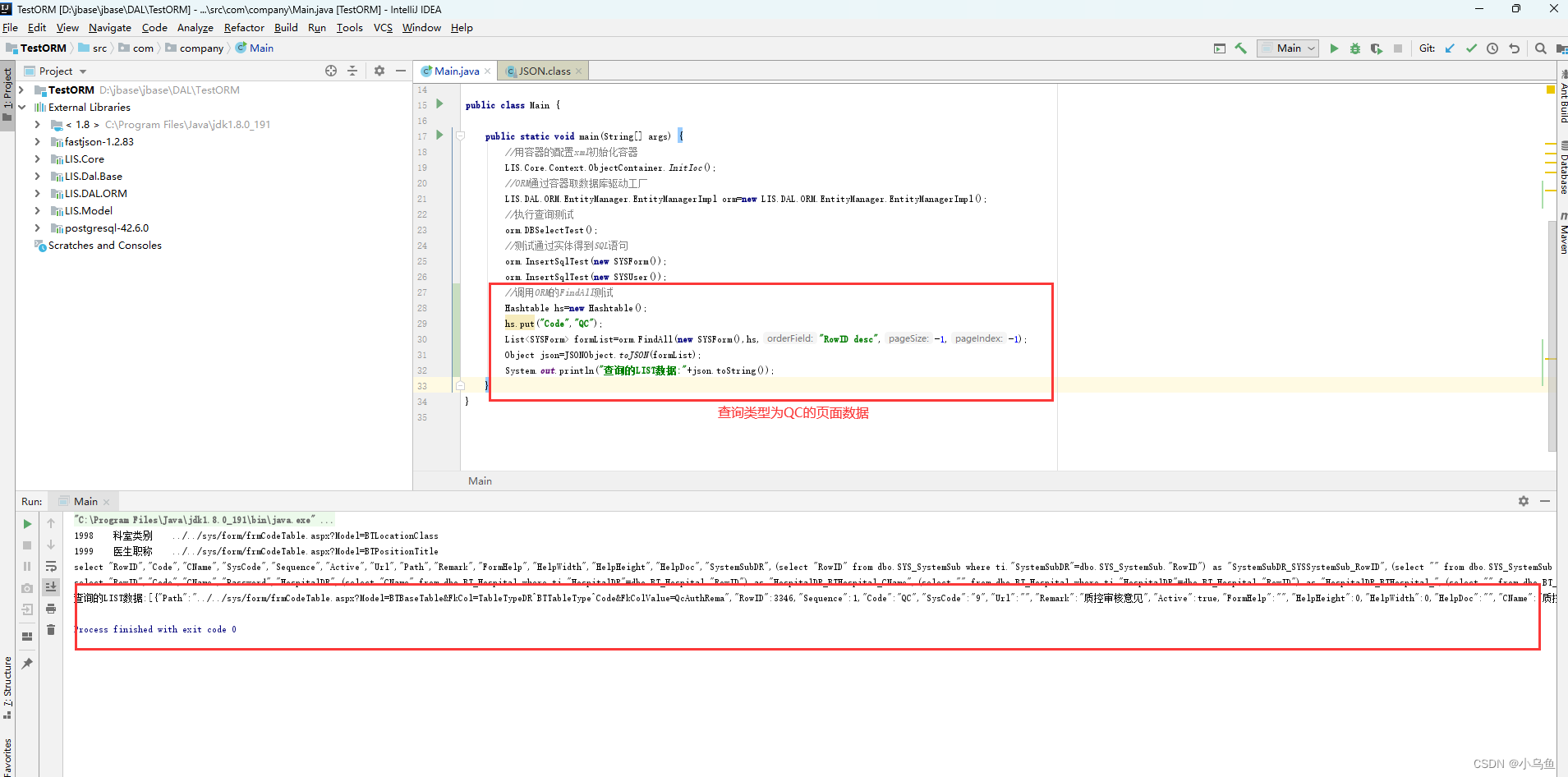
Java实现ORM第一个api-FindAll

经过几天的业余开发&#xff0c;今天终于到ORM对业务api本身的实现了&#xff0c;首先实现第一个查询的api 老的C#定义如下 因为Java的泛型不纯&#xff0c;所以无法用只带泛型的方式实现api&#xff0c;对查询类的api做了调整&#xff0c;第一个参数要求传入实体对象 首先…...

编程日记 2023/10/27 1:25:04

HFSS笔记——求解器和求解分析

文章目录 1、求解器2、求解类型3、自适应网格剖分4、求解频率选择4.1 求解设置项的含义4.2 扫频类型 1、求解器 自从ANSYS将HFSS收购后&#xff0c;其所有的求解器都集成在一起了&#xff0c;点击Project&#xff0c;会显示所有的求解器类型。 其中&#xff0c; HFSS design&…...

编程日记 2023/10/27 1:24:02

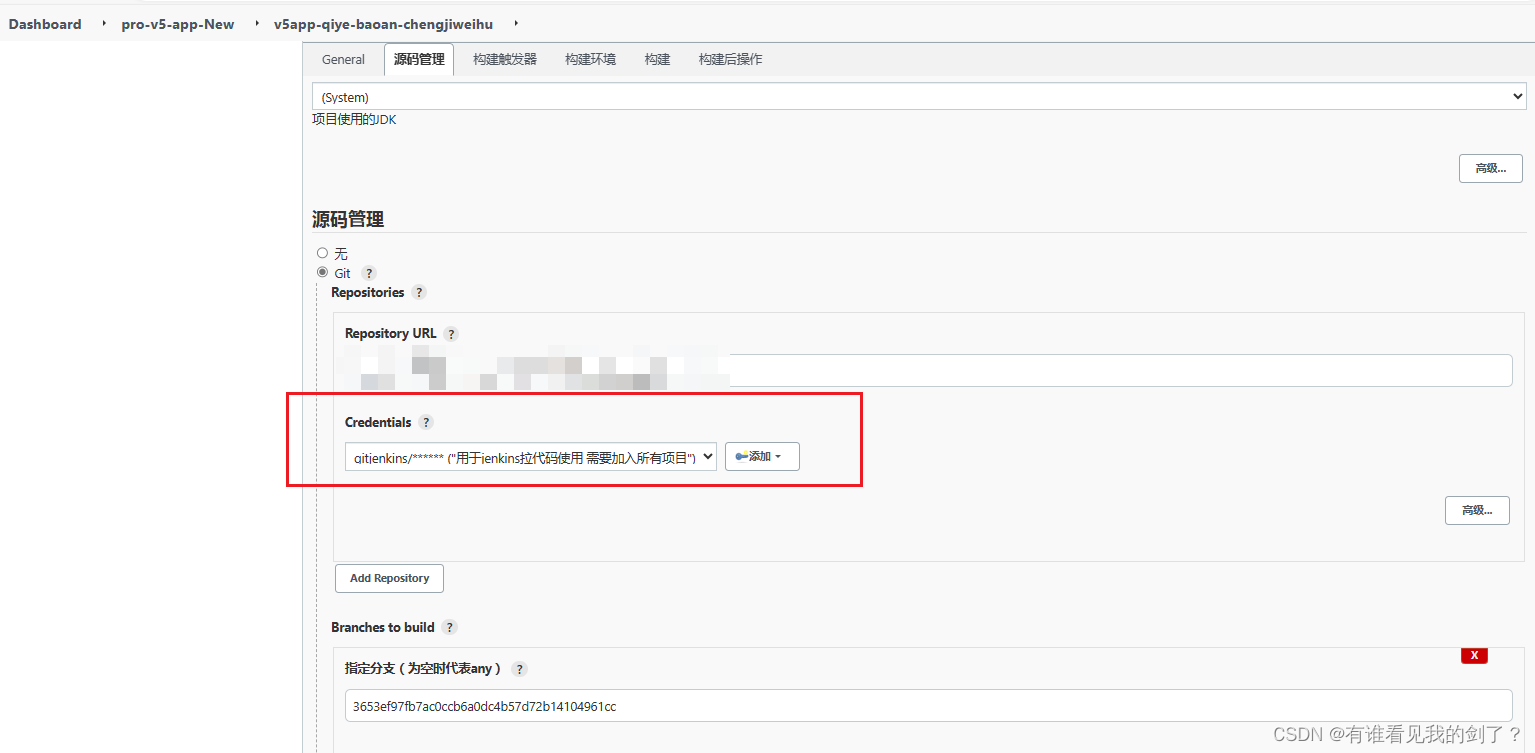
jenkins配置gitlab凭据

下载Credentials Binding插件&#xff08;默认是已经安装了&#xff09; 在凭据配置里添加凭据类型 点击保存 Username with password&#xff1a; 用户名和密码 SSH Username with private 在凭据管理里面添加gitlab账号和密码 点击全局 点击添加凭据&#xff08;版本不同…...

编程日记 2023/10/27 1:23:01

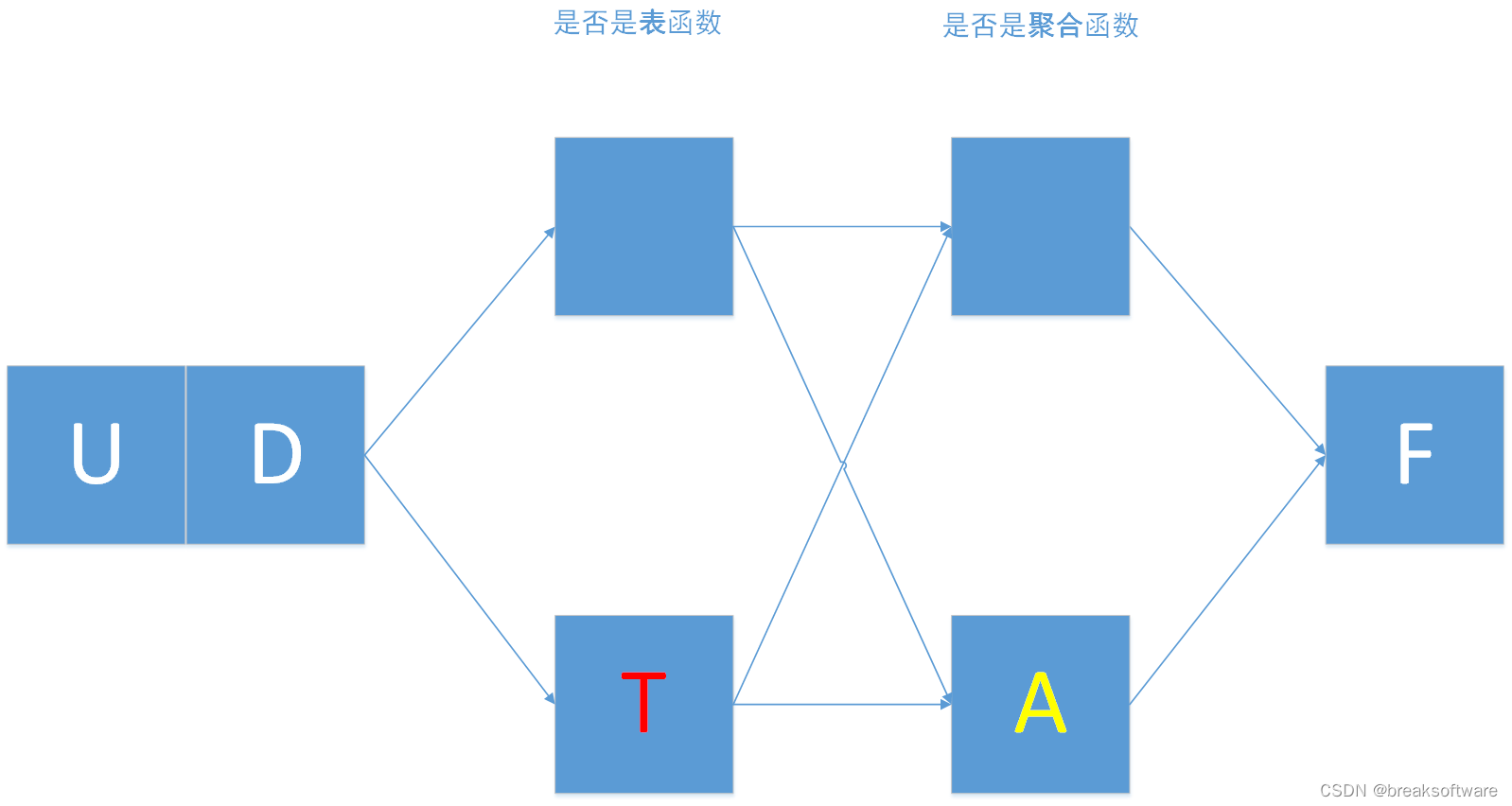
0基础学习PyFlink——用户自定义函数之UDTF

大纲 表值函数完整代码 在《0基础学习PyFlink——用户自定义函数之UDF》中&#xff0c;我们讲解了UDF。本节我们将讲解表值函数——UDTF 表值函数 我们对比下UDF和UDTF def udf(f: Union[Callable, ScalarFunction, Type] None,input_types: Union[List[DataType], DataTy…...

编程日记 2023/10/27 1:22:00

【Java 进阶篇】Java Request 原理详解

在网络应用开发中&#xff0c;HTTP请求是一项常见而关键的任务。当我们使用Java编写网络应用时&#xff0c;了解HTTP请求的工作原理变得至关重要。本文将详细介绍Java中HTTP请求的原理&#xff0c;包括请求的结构、发送请求的方法以及处理请求的过程。 HTTP请求的基本结构 HT…...

编程日记 2023/10/27 1:20:59

13 结构性模式-装饰器模式

1 装饰器模式介绍 在软件设计中,装饰器模式是一种用于替代继承的技术,它通过一种无须定义子类的方式给对象动态的增加职责,使用对象之间的关联关系取代类之间的继承关系. 2 装饰器模式原理 //抽象构件类 public abstract class Component{public abstract void operation(); }…...

编程日记 2023/10/27 1:19:58

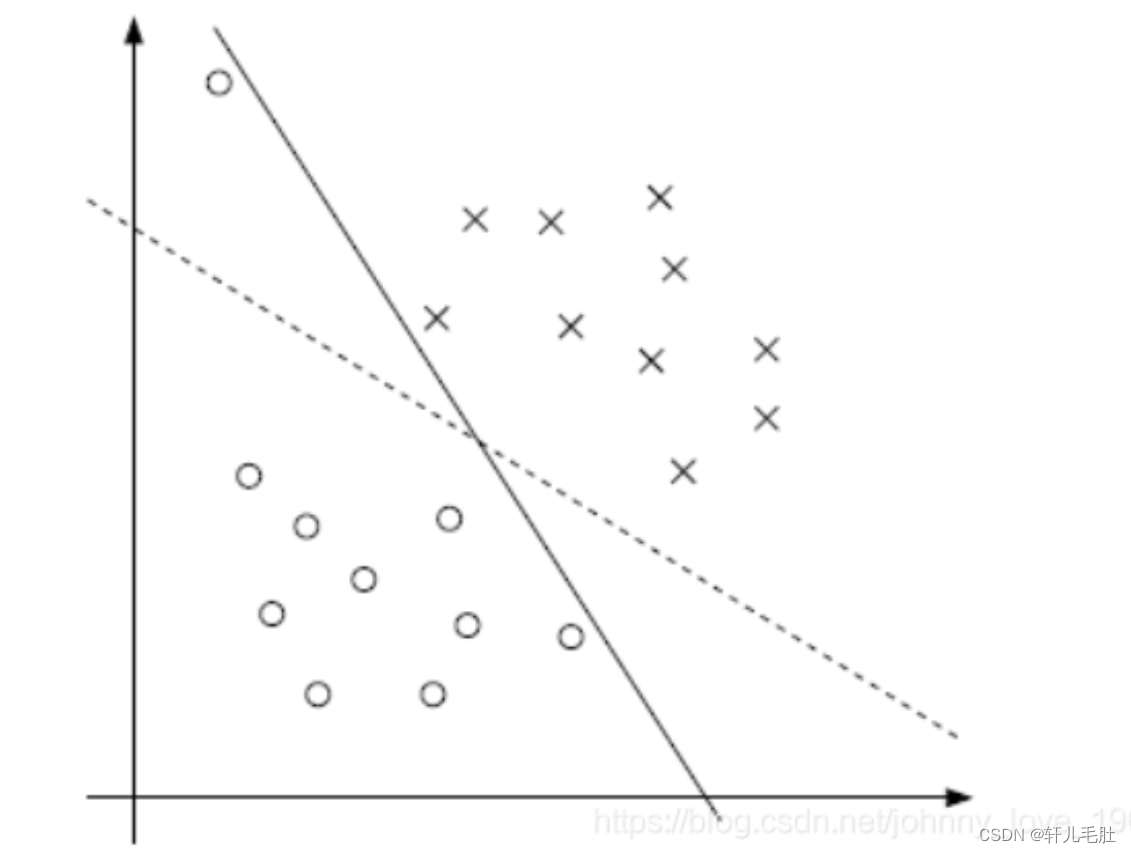
支持向量机（SVM）

一. 什么是SVM 1. 简介 SVM&#xff0c;曾经是一个特别火爆的概念。它的中文名&#xff1a;支持向量机&#xff08;Support Vector Machine, 简称SVM&#xff09;。因为它红极一时&#xff0c;所以关于它的资料特别多&#xff0c;而且杂乱。虽然如此&#xff0c;只要把握住SV…...

编程日记 2023/10/27 1:18:57

Rabbitmq----分布式场景下的应用

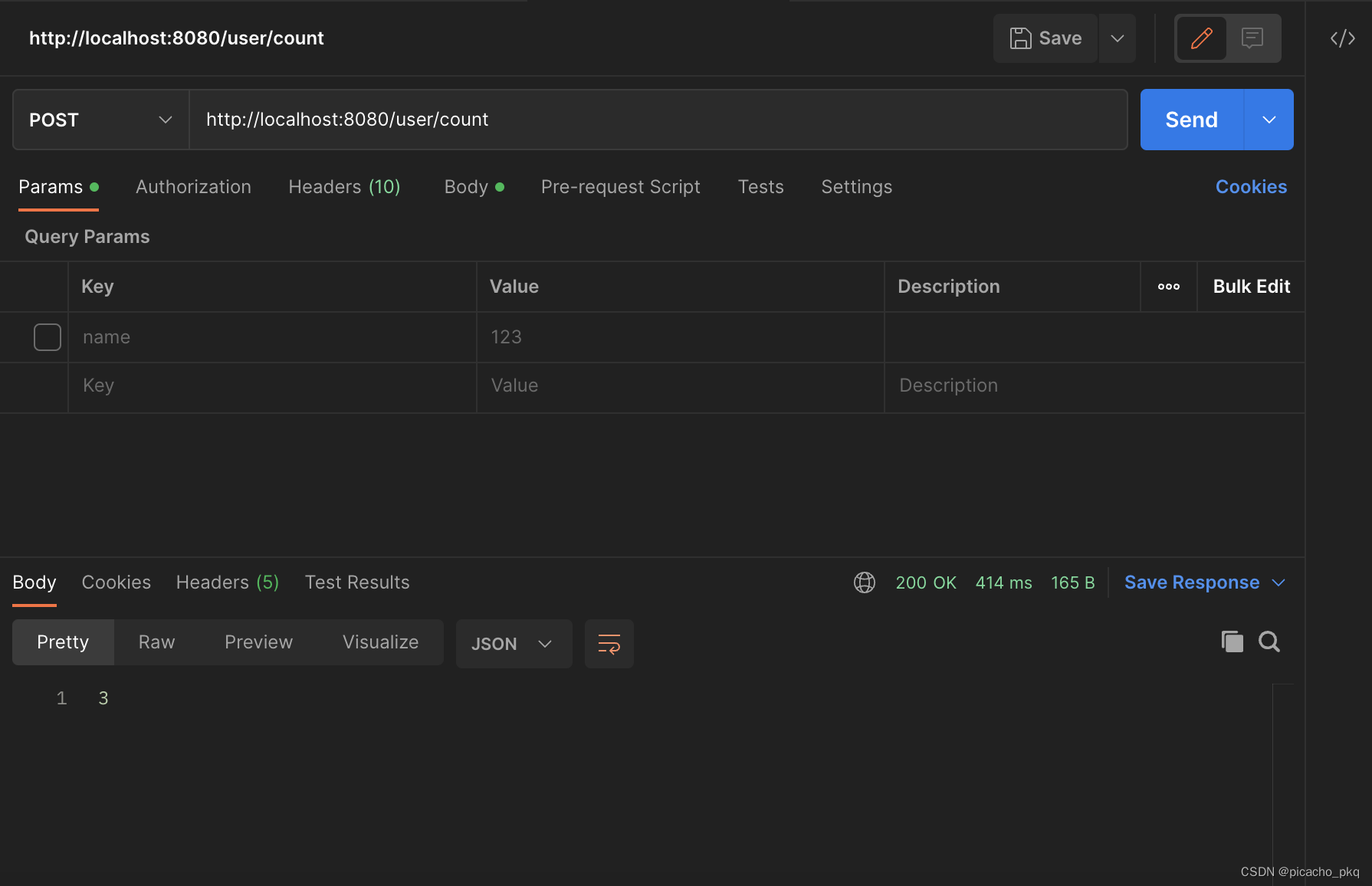
服务异步通信-分布式场景下的应用 如果单机模式忘记也可以看看这个快速回顾rabbitmq,在做学习 消息队列在使用过程中&#xff0c;面临着很多实际问题需要思考&#xff1a; 1.消息可靠性 消息从发送&#xff0c;到消费者接收&#xff0c;会经理多个过程&#xff1a; 其中的每一…...

编程日记 2023/10/27 1:17:56

springboot + redis实现签到与统计功能

在很多项目中都会有签到与统计功能&#xff0c;最容易想到的方案是创建一个签到表来记录每个用户的签到记录&#xff0c;比如设计一个mysql数据库表&#xff1a; CREATE TABLE tb_sign id bigint(20) unsigned NOT NULL AUTOINCREMENT COMMENT 主键, user_id bigint(20) unsig…...

编程日记 2023/10/27 1:16:55

Redis | 数据结构（02）SDS

一、键值对数据库是怎么实现的&#xff1f; 在开始讲数据结构之前&#xff0c;先给介绍下 Redis 是怎样实现键值对&#xff08;key-value&#xff09;数据库的。 Redis 的键值对中的 key 就是字符串对象&#xff0c;而 value 可以是字符串对象&#xff0c;也可以是集合数据类型…...

编程日记 2023/10/27 1:15:54

Linux C语言开发-D7D8运算符

算术运算符&#xff1a;-*/%&#xff0c;浮点数可以参与除法运算&#xff0c;但不能参与取余运算 a%b&#xff1a;表示取模或取余 关系运算符&#xff1a;<,>,>,<,,! 逻辑运算符:!,&&,|| &&,||逻辑运算符是从左到右&#xff0c;依次运算&#…...

编程日记 2023/10/27 1:14:53

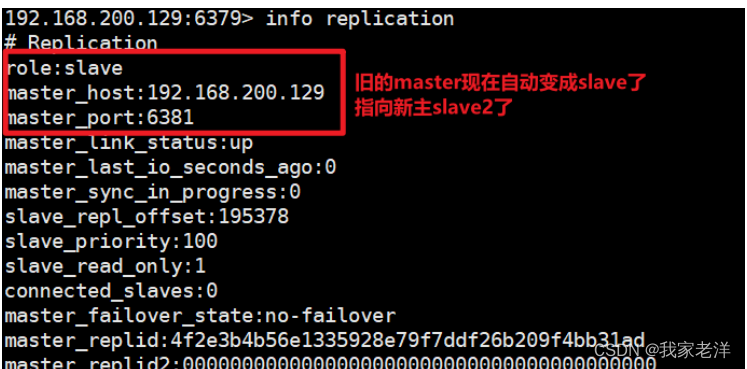
redis 配置主从复制,哨兵模式案例

哨兵(Sentinel)模式 1 . 什么是哨兵模式&#xff1f; 反客为主的自动版&#xff0c;能够自动监控master是否发生故障&#xff0c;如果故障了会根据投票数从slave中挑选一个 作为master&#xff0c;其他的slave会自动转向同步新的master&#xff0c;实现故障自动转义 2 . 原理…...

编程日记 2023/10/27 1:13:53

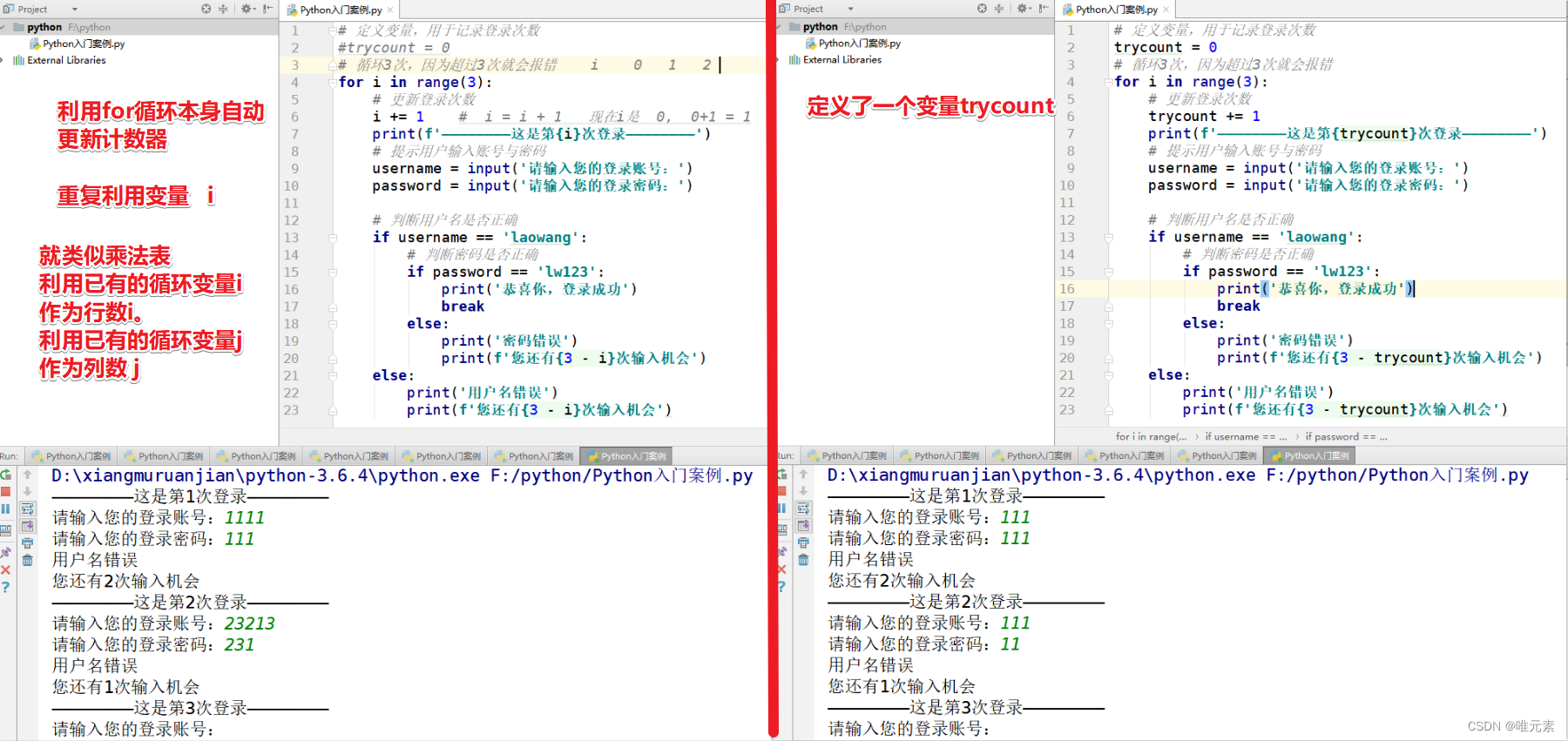
Python---练习：使用for循环实现用户名+密码认证

案例&#xff1a; 用for循环实现用户登录 ① 输入用户名和密码 ② 判断用户名和密码是否正确&#xff08;usernamelaowang&#xff0c;passwordlw123&#xff09; ③ 登录仅有三次机会&#xff0c;超过3次会报错 思考&#xff1a; 用户登陆情况有3种: ① 用户名错误(此时…...

编程日记 2023/10/27 1:12:51

2026横向对比5款H5工具，产品介绍页制作，哪款出片更高级？

制作产品介绍H5时&#xff0c;很多人都会陷入两难&#xff1a;要么模板廉价缺乏质感&#xff0c;撑不起产品调性&#xff1b;要么设计复杂、操作繁琐&#xff0c;新手难以驾驭&#xff1b;要么高级效果需额外付费&#xff0c;性价比大打折扣。产品介绍页的高级感&#xff0c;直…...

编程新知 2026/4/6 4:08:05

Windows下OpenClaw安装指南：一键对接Phi-3-mini-128k-instruct模型

Windows下OpenClaw安装指南&#xff1a;一键对接Phi-3-mini-128k-instruct模型 1. 为什么选择OpenClawPhi-3-mini组合&#xff1f; 去年我在尝试自动化办公流程时&#xff0c;发现市面上的RPA工具要么太笨重&#xff0c;要么需要复杂的编程。直到遇到OpenClaw这个开源智能体框…...

编程新知 2026/4/6 4:05:57

JAVA无人共享无人机赁柜预约小程序源码代码

JAVA无人共享无人机租赁柜预约小程序源码实现方案采用Uniapp框架开发无人共享无人机租赁柜预约小程序&#xff0c;需整合后端Java服务和前端跨平台技术。以下是核心实现方案&#xff1a;技术栈选择前端&#xff1a;Uniapp Vue.js uView UI后端&#xff1a;Spring Boot MyBat…...

编程新知 2026/4/6 3:11:10

吴恩达机器学习第一天

#P2 机器学习的定义定义为赋予计算机在没有明确编程的情况下学习能力的研究领域。给学习算法更多的学习机会&#xff0c;他的表现就会更好。主要类型&#xff1a;监督学习&#xff08;supervised learning)无监督学习&#xff08;unsupervised learning)推荐系统&#xff08;re…...

编程新知 2026/4/6 2:52:32

Element Plus：Vue 3企业级UI组件库的全方位解析与实践指南

Element Plus&#xff1a;Vue 3企业级UI组件库的全方位解析与实践指南 【免费下载链接】element-plus &#x1f389; A Vue.js 3 UI Library made by Element team 项目地址: https://gitcode.com/GitHub_Trending/el/element-plus Element Plus作为基于Vue 3的企业级UI…...

编程新知 2026/4/6 0:34:59

PrimeTime实战指南：从基础STA流程到精准时序报告解析

1. PrimeTime与静态时序分析基础 刚接触PrimeTime时&#xff0c;我和大多数工程师一样被满屏的时序报告搞得头晕眼花。直到把整个设计流程跑通三遍后&#xff0c;才真正理解这个工具的价值。PrimeTime&#xff08;简称PT&#xff09;是Synopsys推出的静态时序分析黄金工具&…...

编程新知 2026/4/5 21:39:28

python binascii

## 关于Base64&#xff0c;你可能需要知道这些 在编程的世界里&#xff0c;数据并不总是以我们熟悉的形式存在。有时候&#xff0c;一段文字、一张图片&#xff0c;或者任何其他类型的数据&#xff0c;需要被转换成另一种形式才能在不同的系统中安全传输或存储。Base64就是这样…...

编程新知 2026/4/5 19:53:31

输入可视化革命：如何用input-overlay消除直播中的操作信息差

输入可视化革命&#xff1a;如何用input-overlay消除直播中的操作信息差 【免费下载链接】input-overlay Show keyboard, gamepad and mouse input on stream 项目地址: https://gitcode.com/gh_mirrors/in/input-overlay 观众为何总是误解你的操作意图&#xff1f; 当…...

编程新知 2026/4/5 19:45:21

从零开始：在Ubuntu 18.04上正确配置CUDA 11.7和bitsandbytes 0.38.0的完整指南

从零构建Ubuntu 18.04下的AI开发环境&#xff1a;CUDA 11.7与bitsandbytes 0.38.0深度配置手册 在深度学习领域&#xff0c;环境配置往往是项目推进的第一道门槛。特别是当我们需要使用bitsandbytes这样的高性能量化工具时&#xff0c;CUDA环境的纯净性与版本匹配度直接决定了后…...

编程新知 2026/4/5 19:23:04

工程师快速解决TVA检测系统常见故障的实操技巧

TVA系统在汽车零部件焊接点检测中需长期连续运行&#xff0c;适配高节拍生产场景&#xff0c;作为负责系统运维的工程师&#xff0c;快速排查与解决常见故障&#xff0c;是保障系统稳定运行的核心职责。在实际运维过程中&#xff0c;不少工程师因对故障原因判断不准确、排查方法…...

编程新知 2026/4/5 18:58:49