LeetCode 1402. 做菜顺序【排序,动态规划;贪心,前缀和,递推】1679
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
一个厨师收集了他 n 道菜的满意程度 satisfaction ,这个厨师做出每道菜的时间都是 1 单位时间。
一道菜的 「 like-time 系数 」定义为烹饪这道菜结束的时间(包含之前每道菜所花费的时间)乘以这道菜的满意程度,也就是 time[i]*satisfaction[i] 。
返回厨师在准备了一定数量的菜肴后可以获得的最大 like-time 系数 总和。
你可以按 任意 顺序安排做菜的顺序,你也可以选择放弃做某些菜来获得更大的总和。
示例 1:
输入:satisfaction = [-1,-8,0,5,-9]
输出:14
解释:去掉第二道和最后一道菜,最大的 like-time 系数和为 (-1*1 + 0*2 + 5*3 = 14) 。每道菜都需要花费 1 单位时间完成。
示例 2:
输入:satisfaction = [4,3,2]
输出:20
解释:可以按照任意顺序做菜 (2*1 + 3*2 + 4*3 = 20)
示例 3:
输入:satisfaction = [-1,-4,-5]
输出:0
解释:大家都不喜欢这些菜,所以不做任何菜就可以获得最大的 like-time 系数。
提示:
n == satisfaction.length1 <= n <= 500-1000 <= satisfaction[i] <= 1000
解法1 排序+动态规划
假设我们只能选一道菜,那么我们应该如何选择呢?显然,选择满意程度最大的那一道菜 s 0 s_0 s0 是最优的,并且需要验证是否满足 s 0 > 0 s_0 > 0 s0>0 。
假设现在有两道菜 s 0 , s 1 s_0, s_1 s0,s1 ,则此时应该是先选 s 0 s_0 s0 还是先选 s 1 s_1 s1 呢?显然,应先选择小的那道菜,再选择大的那道菜。假设 s 0 < s 1 s_0 < s_1 s0<s1 ,此时如果先选择满意小的菜,再选择满意度大的菜则此时的喜爱时间为 s 0 + 2 s 1 s_0 + 2s_1 s0+2s1 ;此时如果先选择满意大的菜,再选择满意小的菜则此时的喜爱时间为 s 1 + 2 s 0 s_1 + 2s_0 s1+2s0 ,由于 s 0 < s 1 s_0 < s_1 s0<s1 ,显然 s 0 + 2 s 1 > s 1 + 2 s 0 s_0 + 2s_1 > s_1 + 2s_0 s0+2s1>s1+2s0 。
当然上述问题还需要具体分析,因为涉及到 s 0 , s 1 s_0, s_1 s0,s1 可能小于 0 0 0 情形,但无论取值 s 0 , s 1 s_0, s_1 s0,s1 如何,我们都应该尽量先选择满意度小的,后选择满意度大的。可以根据 排序不等式 得到该结论。
根据上述贪心原则,显然满意度越大的菜越应该尽量越往后选,应对 n n n 道菜按照满意度的大小进行排序,满意度越大的菜应该越往后排。
如果第 i i i 次选了第 j j j 道菜,则此时第 j j j 道菜的喜爱时间为 i × satisfaction [ j ] i \times \textit{satisfaction}[j] i×satisfaction[j] 。对于每道菜来说,可以选或者可以不选,此时则可以转换为「 0-1 \text{0-1} 0-1 背包」问题,等价于求在 n n n 个物品中选择 m m m 个时可以获得的最大喜爱时间,其中 m ∈ [ 0 , n ] m \in [0,n] m∈[0,n] 。
设 dp [ i ] [ j ] \textit{dp}[i][j] dp[i][j] 表示前 i i i 道菜中选择 j j j 道菜时可以得到的最大喜爱时间,且满足 i ≥ j i \ge j i≥j ,则此时对于第 i i i 道菜来说有以下两种选择:
- 第 i i i 道菜在第 j j j 次被选择,则此时需要在前 i − 1 i-1 i−1 道菜中选择 j − 1 j-1 j−1 道菜,则此时 dp [ i ] [ j ] = max ( dp [ i ] [ j ] , dp [ i − 1 ] [ j − 1 ] + j × satisfaction [ i ] ) \textit{dp}[i][j] = \max(\textit{dp}[i][j], \textit{dp}[i-1][j-1] + j \times \textit{satisfaction}[i]) dp[i][j]=max(dp[i][j],dp[i−1][j−1]+j×satisfaction[i])
- 第 i i i 道菜在第 j j j 次没有被选择,则此时需要在前 i − 1 i-1 i−1 道菜中选择 j j j 道菜,此时需要满足 i − 1 ≥ j i -1 \ge j i−1≥j ,则此时 dp [ i ] [ j ] = max ( dp [ i ] [ j ] , dp [ i − 1 ] [ j ] ) \textit{dp}[i][j] = \max(\textit{dp}[i][j], \textit{dp}[i-1][j]) dp[i][j]=max(dp[i][j],dp[i−1][j])
我们按照上述递推公式计算出 n n n 道菜中选择 x x x 道菜的最大喜爱时间, x x x 的取值为 x ∈ [ 0 , n ] x \in [0, n] x∈[0,n] ,则此时可以得到的最大喜爱时间为 max ( dp [ n ] [ x ] ) \max (\textit{dp}[n][x]) max(dp[n][x]) 。
为什么需要对数组进行排序,才可以使用动态规划?
假设现在有 i i i 道菜,此时 i i i 道菜中满意度最大的为第 j j j 道菜,它的满意度 satisfaction [ j ] \textit{satisfaction}[j] satisfaction[j] ,假设它在数组中的排序为 i ′ i^{'} i′ ,则此时 i ′ < i i^{'} < i i′<i ,无法取到 i i i ,即此时它的喜爱时间一定无法取到 i × satisfaction [ j ] i \times \textit{satisfaction}[j] i×satisfaction[j] ,则此时一定无法满足最优解。
class Solution {
public:int maxSatisfaction(vector<int>& satisfaction) {int n = satisfaction.size();sort(satisfaction.begin(), satisfaction.end());vector<vector<int>> dp(n + 1, vector<int>(n + 1));int ans = 0;// dp[i][j]表示前i道菜中选择j道菜时可以得到的最大喜爱时间// dp[i][j]=max(dp[i][j], dp[i-1][j-1]+j*s[i])// dp[i][j]=max(dp[i][j], dp[i-1][j]), if i-1>=jfor (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i][j] = dp[i - 1][j - 1] + satisfaction[i - 1] * j;if (j < i) dp[i][j] = max(dp[i - 1][j], dp[i][j]);ans = max(ans, dp[i][j]);}}return ans;}
};
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2) ,其中 n n n 表示数组 s a t i s f a c t i o n satisfaction satisfaction 的长度。排序需要的时间为 O ( n log n ) O(n\log n) O(nlogn) ,求解动态规划需要的时间为 O ( n 2 ) O(n^2) O(n2) ,因此总的时间复杂度为 O ( n 2 ) O(n^2) O(n2) 。
- 空间复杂度: O ( n 2 ) O(n^2) O(n2) ,其中 n n n 表示数组 s a t i s f a c t i o n satisfaction satisfaction 的长度。我们需要所有动态规划的子状态,一共有 n 2 n^2 n2 中子状态,需要的空间为 O ( n 2 ) O(n^2) O(n2) 。
解法2 贪心+前缀和+递推
为了方便计算,把 a a a 从大到小排序。来看看做 k = 1 , 2 , 3 k=1,2,3 k=1,2,3 道菜时,对应的总和 f ( k ) f(k) f(k) 是多少。
- k = 1 k=1 k=1 时,总和为 f ( 1 ) = a [ 0 ] f(1)=a[0] f(1)=a[0] 。
- k = 2 k=2 k=2 时,总和为 f ( 2 ) = 2 ⋅ a [ 0 ] f(2)=2⋅a[0] f(2)=2⋅a[0] 。
- k = 3 k=3 k=3 时,总和为 f ( 3 ) = 3 ⋅ a [ 0 ] + 2 ⋅ a [ 1 ] + a [ 2 ] f(3)=3\cdot a[0] + 2\cdot a[1] + a[2] f(3)=3⋅a[0]+2⋅a[1]+a[2] 。
为了快速地算出每个 f ( k ) f(k) f(k) ,我们需要找到 f ( k ) f(k) f(k) 的递推式。观察上面列出的式子,你能找到递推式吗?先把 f ( k ) f(k) f(k) 的式子列出来:
f ( k ) = k ⋅ a [ 0 ] + ( k − 1 ) ⋅ a [ 1 ] + ⋯ + 2 ⋅ a [ k − 2 ] + a [ k − 1 ] f(k)=k\cdot a[0] + (k-1)\cdot a[1] + \cdots + 2\cdot a[k-2] + a[k-1] f(k)=k⋅a[0]+(k−1)⋅a[1]+⋯+2⋅a[k−2]+a[k−1]
每一项去掉一个 a [ i ] a[i] a[i] ,得到:
( k − 1 ) ⋅ a [ 0 ] + ( k − 2 ) ⋅ a [ 1 ] + ⋯ + a [ k − 2 ] (k-1)\cdot a[0] + (k-2)\cdot a[1] + \cdots + a[k-2] (k−1)⋅a[0]+(k−2)⋅a[1]+⋯+a[k−2]
这正是 f ( k − 1 ) f(k-1) f(k−1) 。所以有
f ( k ) = f ( k − 1 ) + ( a [ 0 ] + a [ 1 ] + ⋯ + a [ k − 1 ] ) f(k) = f(k-1) + (a[0] + a[1] + \cdots + a[k-1]) f(k)=f(k−1)+(a[0]+a[1]+⋯+a[k−1])
右边的和式是 a a a 的前缀和,我们可以一边遍历 a a a ,一边把 a [ i ] a[i] a[i] 累加到一个变量 s s s 中。这样就可以 O ( 1 ) \mathcal{O}(1) O(1) 地从 f ( k − 1 ) f(k-1) f(k−1) 递推得到 f ( k ) f(k) f(k) 了。
答案为 f ( 0 ) , f ( 1 ) , f ( 2 ) , ⋯ , f ( n ) f(0), f(1), f(2),\cdots, f(n) f(0),f(1),f(2),⋯,f(n) 中的最大值。
实现细节:想一想 s s s 是怎么变化的。由于数组是从大到小排序的,(一般地)会先遇到正数,再遇到负数,所以(一般地) s s s 会先变大,再变小。
如果 s ≤ 0 s\le 0 s≤0 ,那么后面的 a [ i ] a[i] a[i] 必然都是负数,我们不可能得到更大的 f ( k ) f(k) f(k) ,退出循环。
代码实现时,可以只用一个变量表示 f f f 。由于在退出循环之前 s s s 都是大于 0 0 0 的,所以 f ( k ) > f ( k − 1 ) f(k) > f(k-1) f(k)>f(k−1) ,因此退出循环时的 fff 就是最终答案。
class Solution {
public:int maxSatisfaction(vector<int>& satisfaction) {sort(satisfaction.rbegin(), satisfaction.rend());int f = 0; // f(0) = 0int s = 0; // satisfaction 的前缀和for (int x : satisfaction) {s += x;if (s <= 0) { // 后面不可能找到更大的 f(k)break;}f += s; // f(k) = f(k-1) + s}return f;}
};
复杂度分析:
- 时间复杂度: O ( n log n ) \mathcal{O}(n\log n) O(nlogn) ,其中 n n n 为 a a a 的长度。瓶颈在排序上。
- 空间复杂度: O ( 1 ) \mathcal{O}(1) O(1) 。忽略排序的栈开销。
相关文章:

LeetCode 1402. 做菜顺序【排序,动态规划;贪心,前缀和,递推】1679
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

【多线程】探索Java中的多线程编程
标题:探索Java中的多线程编程 摘要: Java是一种广泛使用的编程语言,具有强大的多线程编程能力。本文将深入探讨Java中的多线程编程,包括线程的创建、同步与互斥、线程池的使用以及常见的多线程编程模式。通过示例代码和详细解释&…...

【算法题】翻转对
题目: 给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。 你需要返回给定数组中的重要翻转对的数量。 示例 1: 输入: [1,3,2,3,1] 输出: 2 示例 2: 输入: [2,4,3,5,1] 输出: 3 注意: 给定数组的长…...
适用于 Mac 或 Windows 的 4 种最佳 JPEG/PNG图片 恢复软件
您的计算机或外部存储驱动器上很可能有大量 JPEG /PNG图片照片,但不知何故,您意识到一些重要的 JPEG /PNG图片文件丢失或被删除,它们对您来说意义重大,您想要找回它们. 4 种最佳 JPEG/PNG图片 恢复软件 要成功执行 JPEG /PNG图片…...

位置信息API
位置信息API 一、获取当前位置:wx.getLocation(object)二、选择位置:wx.chooseLocation(object)三、打开位置:wx.openLocation(object)四、监听位置事件五、地图组件控制API六、收货地址API:wx.chooseAddress(object) 一、获取当前…...
MySQL——九、SQL编程
MySQL 一、触发器1、触发器简介2、创建触发器3、一些常见示例 二、存储过程1、什么是存储过程或者函数2、优点3、存储过程创建与调用 三、存储函数1、存储函数创建和调用2、修改存储函数3、删除存储函数 四、游标1、声明游标2、打开游标3、使用游标4、关闭游标游标案例 一、触发…...

threejs(4)-纹理材质高级操作
一、纹理重复_缩放_旋转_位移操作 // 导入threejs import * as THREE from "three"; // 导入轨道控制器 import { OrbitControls } from "three/examples/jsm/controls/OrbitControls.js"; // 导入lil.gui import { GUI } from "three/examples/jsm/l…...

Redis | 数据结构(01)
这里写自定义目录标题 Redis 速度快的原因除了它是内存数据库,使得所有的操作都在内存上进行之外,还有一个重要因素,它实现的数据结构,使得我们对数据进行增删查改操作时,Redis 能高效的处理。 因此,这次我…...

一文详解多模态大模型发展及高频因子计算加速GPU算力 | 英伟达显卡被限,华为如何力挽狂澜?
★深度学习、机器学习、多模态大模型、深度神经网络、高频因子计算、GPT-4、预训练语言模型、Transformer、ChatGPT、GenAI、L40S、A100、H100、A800、H800、华为、GPU、CPU、英伟达、NVIDIA、卷积神经网络、Stable Diffusion、Midjourney、Faster R-CNN、CNN 随着人工智能技术…...
debian 10 安装apache2 zabbix
nginx 可以略过,改为apache2 apt updateapt-get install nginx -ynginx -v nginx version: nginx/1.14.2mysql 安装参考linux debian10 安装mysql5.7_debian apt install mysql5.7-CSDN博客 Install and configure Zabbix for your platform a. Install Zabbix re…...
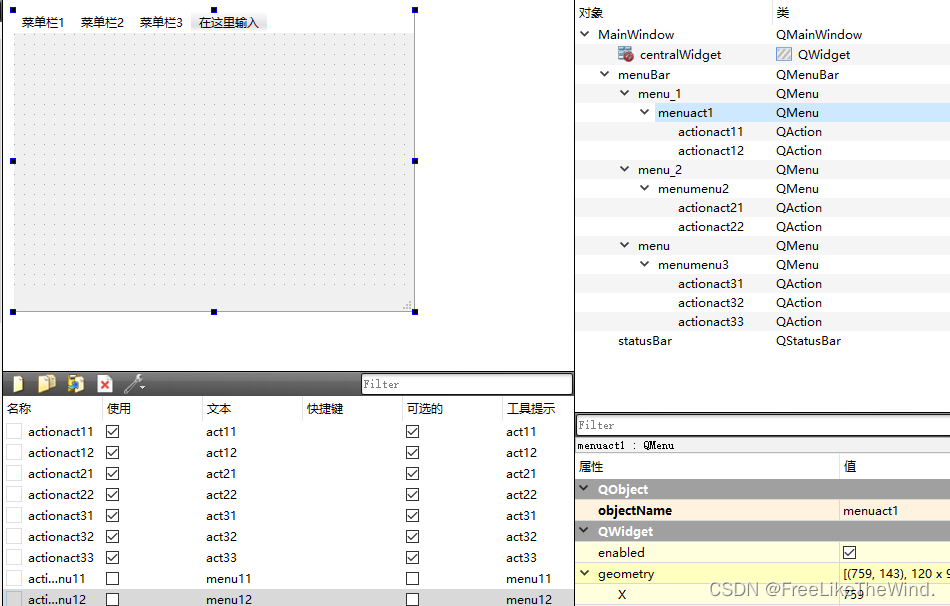
Qt之菜单栏、工具栏、状态栏介绍及工具栏QAction的动态增删显示实现方式
目的 端应用程序或者编辑器基本都支持工具栏快捷功能的动态增删,即通过在菜单栏上打钩就可以在工具栏上看到相应功能的快捷按钮,取消打钩则在工具栏上就移除了该功能的快捷按钮。那么Qt如何实现这个功能,本篇目的就是记录实现此功能的方法及思…...
十四天学会C++之第八天:文件操作
1. 文件的打开和关闭 文件操作的基本概念。打开文件:使用fstream库打开文件以供读写。关闭文件:确保文件在使用完毕后正确关闭。 文件的打开和关闭:C 文件操作入门 在C编程中,文件操作是一项重要的任务,可以读取和写…...
×(N-1)棋盘的解的情况推出N×N棋盘的解的情况的N皇后问题)
基于(N-1)×(N-1)棋盘的解的情况推出N×N棋盘的解的情况的N皇后问题
N皇后问题是一个比较经典的问题,其主要目标是在NN的棋盘上,放置N个皇后,要求所有皇后之间不能互相攻击,即任意两个皇后不能处在同一行、同一列或同一对角线上。解决该问题可以采用递归的方式,基于(N-1)棋盘的解的情况推…...
Vue mixin混入
可以把多个组件中共有的配置提取出来构成一个混入。 一、配置混入 (一) 创建mixin.js 这里的名字可以自定义,但是为了方便识别,多数场景下都写mixin。 mixin.js 要创建在src目录下,与main.js平级: &…...
基于 FFmpeg 的跨平台视频播放器简明教程(十):在 Android 运行 FFmpeg
系列文章目录 基于 FFmpeg 的跨平台视频播放器简明教程(一):FFMPEG Conan 环境集成基于 FFmpeg 的跨平台视频播放器简明教程(二):基础知识和解封装(demux)基于 FFmpeg 的跨平台视频…...

正点原子嵌入式linux驱动开发——Linux LCD驱动
LCD是很常用的一个外设,通过LCD可以显示绚丽的图片、界面等,提交人机交互的效率。STM32MP1提供了一个LTDC接口用于连接RGB接口的液晶屏。本章就来学校一下如何在Linux下驱动LCD屏。 LCD和LTDC简介 LCD简介 这里在当时学习stm32裸机开发的时候就学过了…...
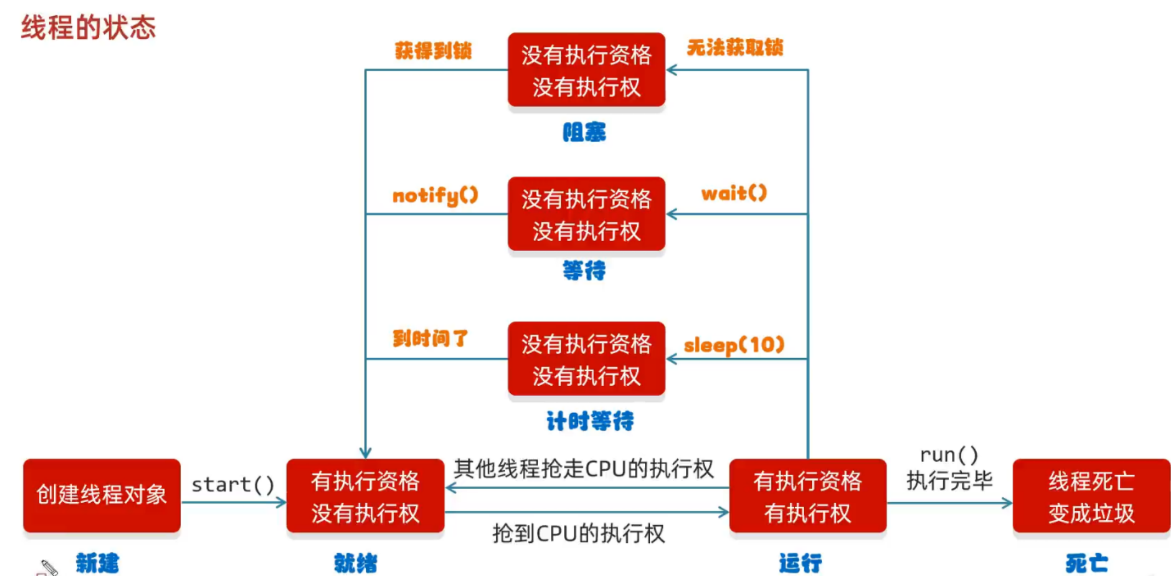
2-Java进阶知识总结-6-多线程
文章目录 多线程--基本概念并发和并行进程和线程多线程 多线程--实现方式一,继承Thread类方法介绍实现步骤注意事项 方式二,实现Runnable接口Thread构造方法实现步骤 方式三,实现Callable接口方法介绍实现步骤 三种多线程实现方法对比 多线程…...
openwrt下游设备在校园网(DLUT-LingShui)中使用ipv6网络
背景:校园网最多支持6台设备的无感认证,需要使用路由器(本人使用openwrt系统)为更多的设备提供网络,但校园网分配的ipv6地址子网为/128,不能为路由器下的设备分配全球ipv6地址,因此需要使用nat6转发下游设备的局域网ip…...
10个基于.Net开发的Windows开源软件项目
1、基于.NET的强大软件开发工具 一个基于.Net Core构建的简单、跨平台快速开发框架。JNPF开发平台前后端封装了上千个常用类,方便扩展;集成了代码生成器,支持前后端业务代码生成,满足快速开发,提升工作效率;…...
Java多线程秘籍,掌握这5种方法,让你的代码优化升级
介绍5种多线程方法,助您提高编码效率! 如果您的应用程序与那些能够同时处理多个任务的应用程序相比表现不佳,很可能是因为它是单线程的。解决这个问题的方法之一是采用多线程技术。 以下是一些可以考虑的方法: 线程(…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
