当前位置： 首页 > news >正文

『第四章』一见倾心：初识小雨燕（上）

news 2026/2/7 14:40:43

在这里插入图片描述

在本篇博文中,您将学到如下内容:

  • 1. 基本数据类型
  • 2. 基本操作符
  • 3. 枚举和结构
  • 4. 类和 Actor
  • 5. 属性、方法与访问控制
  • 6. 聚集
  • 总结

夜月一帘幽梦，春风十里柔情。
无声交谈情意深，一见心曲绕梁成。

1. 基本数据类型

无论是 macOS 还是 iOS 上的开发，Swift 基础类型和功能都内置于 Foundation 框架中。所以我们一般需要首先导入它：

import Foundation

注意，UIKit、SwiftUI 等框架本身就导入了 Foundation ，所以在这种情况下我们就无需重复导入了（当然重复导入也不会有什么问题）。

和所有其它高级语言类似，Swift 本身也包含

相关文章：

『第四章』一见倾心：初识小雨燕（上）

在本篇博文中,您将学到如下内容: 1. 基本数据类型2. 基本操作符3. 枚举和结构4. 类和 Actor5. 属性、方法与访问控制6. 聚集总结夜月一帘幽梦，春风十里柔情。 无声交谈情意深，一见心曲绕梁成。 1. 基本数据类型 无论是 macOS 还是 iOS 上的开发，Swift 基础类型和功能都内置于…...

编程日记 2023/10/27 2:27:26

elasticsearch-7.9.3 单节点启动配置

一、elasticsearch-7.9.3 单节点启动配置 node.name: node-1 network.host: 192.168.227.128 http.port: 9200 discovery.seed_hosts: ["192.168.227.128"] node.max_local_storage_nodes: 1 discovery.type: single-node二、kibana-7.9.3-linux-x86_64 单节点启动配…...

编程日记 2023/10/27 2:26:25

【2024秋招】2023-10-9 同花顺后端笔试题

1 Hashmap mp new hashmap（50）的大小扩充了几次 初时应该就给了这么多空间，在不考虑添加元素，所以扩容为0次 2 算数表达式的中缀为ab*c-d/e，后缀为abc*de/-，前缀是？ 3 50M电信带宽&#xff…...

编程日记 2023/10/27 2:24:23

完美的错误处理：Go 语言最佳实践分享

Go 语言是一门非常流行的编程语言，由于其高效的并发编程和出色的网络编程能力，越来越受到广大开发者的青睐。在任何编程语言中，错误处理都是非常重要的一环，它关系到程序的健壮性和可靠性。Go 语言作为一门现代化的编程语言&#…...

编程日记 2023/10/27 2:23:23

vue首页多模块布局（标题布局）

<template><div class"box"><div class"content"><div class"box1" style"background-color: rgb(245,23,156)">第一个</div><div class"box2" style"background-color: rgb(12,233,…...

编程日记 2023/10/27 2:22:21

嵌入式系统＞嵌入式硬件知识

AI芯片的特点包括 &#xff1a;新型计算范式AI芯片的关键特征&#xff1a; 1、新型的计算范式 AI 计算既不脱离传统计算&#xff0c;也具有新的计算特质&#xff0c;如处理的内容往往是非结构化数据&#xff08;视频、图片等&#xff09;。处理的过程通常需要很大的计算量&am…...

编程日记 2023/10/27 2:21:20

LeetCode 1402. 做菜顺序【排序,动态规划；贪心,前缀和,递推】1679

本文属于「征服LeetCode」系列文章之一&#xff0c;这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁&#xff0c;本系列将至少持续到刷完所有无锁题之日为止&#xff1b;由于LeetCode还在不断地创建新题&#xff0c;本系列的终止日期可能是永远。在这一系列刷题文章…...

编程日记 2023/10/27 2:20:19

【多线程】探索Java中的多线程编程

标题&#xff1a;探索Java中的多线程编程 摘要&#xff1a; Java是一种广泛使用的编程语言&#xff0c;具有强大的多线程编程能力。本文将深入探讨Java中的多线程编程&#xff0c;包括线程的创建、同步与互斥、线程池的使用以及常见的多线程编程模式。通过示例代码和详细解释&…...

编程日记 2023/10/27 2:19:17

【算法题】翻转对

题目&#xff1a; 给定一个数组 nums &#xff0c;如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。 你需要返回给定数组中的重要翻转对的数量。 示例 1: 输入: [1,3,2,3,1] 输出: 2 示例 2: 输入: [2,4,3,5,1] 输出: 3 注意: 给定数组的长…...

编程日记 2023/10/27 2:18:17

适用于 Mac 或 Windows 的 4 种最佳 JPEG/PNG图片 恢复软件

您的计算机或外部存储驱动器上很可能有大量 JPEG /PNG图片照片&#xff0c;但不知何故&#xff0c;您意识到一些重要的 JPEG /PNG图片文件丢失或被删除&#xff0c;它们对您来说意义重大&#xff0c;您想要找回它们. 4 种最佳 JPEG/PNG图片 恢复软件 要成功执行 JPEG /PNG图片…...

编程日记 2023/10/27 2:17:15

位置信息API

位置信息API 一、获取当前位置&#xff1a;wx.getLocation(object)二、选择位置&#xff1a;wx.chooseLocation(object)三、打开位置&#xff1a;wx.openLocation(object)四、监听位置事件五、地图组件控制API六、收货地址API&#xff1a;wx.chooseAddress(object) 一、获取当前…...

编程日记 2023/10/27 2:16:12

MySQL——九、SQL编程

MySQL 一、触发器1、触发器简介2、创建触发器3、一些常见示例 二、存储过程1、什么是存储过程或者函数2、优点3、存储过程创建与调用 三、存储函数1、存储函数创建和调用2、修改存储函数3、删除存储函数 四、游标1、声明游标2、打开游标3、使用游标4、关闭游标游标案例 一、触发…...

编程日记 2023/10/27 2:14:10

threejs(4)-纹理材质高级操作

一、纹理重复_缩放_旋转_位移操作 // 导入threejs import * as THREE from "three"; // 导入轨道控制器 import { OrbitControls } from "three/examples/jsm/controls/OrbitControls.js"; // 导入lil.gui import { GUI } from "three/examples/jsm/l…...

编程日记 2023/10/27 2:13:09

Redis | 数据结构（01）

这里写自定义目录标题 Redis 速度快的原因除了它是内存数据库&#xff0c;使得所有的操作都在内存上进行之外&#xff0c;还有一个重要因素&#xff0c;它实现的数据结构&#xff0c;使得我们对数据进行增删查改操作时&#xff0c;Redis 能高效的处理。 因此&#xff0c;这次我…...

编程日记 2023/10/27 2:12:07

一文详解多模态大模型发展及高频因子计算加速GPU算力 | 英伟达显卡被限，华为如何力挽狂澜？

★深度学习、机器学习、多模态大模型、深度神经网络、高频因子计算、GPT-4、预训练语言模型、Transformer、ChatGPT、GenAI、L40S、A100、H100、A800、H800、华为、GPU、CPU、英伟达、NVIDIA、卷积神经网络、Stable Diffusion、Midjourney、Faster R-CNN、CNN 随着人工智能技术…...

编程日记 2023/10/27 2:11:06

debian 10 安装apache2 zabbix

nginx 可以略过&#xff0c;改为apache2 apt updateapt-get install nginx -ynginx -v nginx version: nginx/1.14.2mysql 安装参考linux debian10 安装mysql5.7_debian apt install mysql5.7-CSDN博客 Install and configure Zabbix for your platform a. Install Zabbix re…...

编程日记 2023/10/27 2:10:05

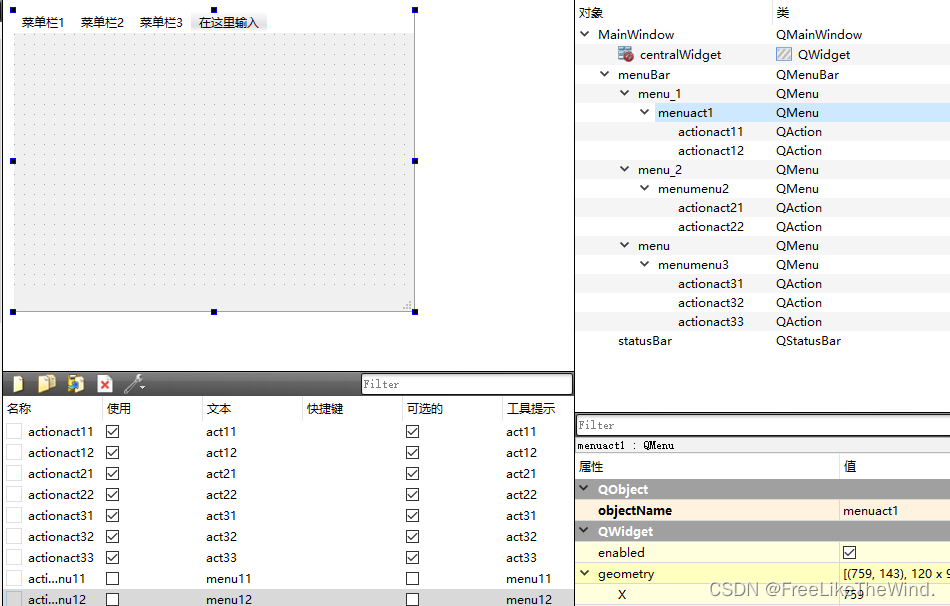
Qt之菜单栏、工具栏、状态栏介绍及工具栏QAction的动态增删显示实现方式

目的 端应用程序或者编辑器基本都支持工具栏快捷功能的动态增删&#xff0c;即通过在菜单栏上打钩就可以在工具栏上看到相应功能的快捷按钮&#xff0c;取消打钩则在工具栏上就移除了该功能的快捷按钮。那么Qt如何实现这个功能&#xff0c;本篇目的就是记录实现此功能的方法及思…...

编程日记 2023/10/27 2:09:04

十四天学会C++之第八天：文件操作

1. 文件的打开和关闭 文件操作的基本概念。打开文件&#xff1a;使用fstream库打开文件以供读写。关闭文件&#xff1a;确保文件在使用完毕后正确关闭。 文件的打开和关闭&#xff1a;C 文件操作入门 在C编程中&#xff0c;文件操作是一项重要的任务&#xff0c;可以读取和写…...

编程日记 2023/10/27 2:08:04

基于(N-1)×(N-1)棋盘的解的情况推出N×N棋盘的解的情况的N皇后问题

N皇后问题是一个比较经典的问题&#xff0c;其主要目标是在NN的棋盘上&#xff0c;放置N个皇后&#xff0c;要求所有皇后之间不能互相攻击&#xff0c;即任意两个皇后不能处在同一行、同一列或同一对角线上。解决该问题可以采用递归的方式&#xff0c;基于(N-1)棋盘的解的情况推…...

编程日记 2023/10/27 2:07:03

Vue mixin混入

可以把多个组件中共有的配置提取出来构成一个混入。 一、配置混入 &#xff08;一&#xff09; 创建mixin.js 这里的名字可以自定义&#xff0c;但是为了方便识别&#xff0c;多数场景下都写mixin。 mixin.js 要创建在src目录下&#xff0c;与main.js平级&#xff1a; &…...

编程日记 2023/10/27 2:06:02

地震勘探——干扰波识别、井中地震时距曲线特点

目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波&#xff1a;可以用来解决所提出的地质任务的波&#xff1b;干扰波&#xff1a;所有妨碍辨认、追踪有效波的其他波。 地震勘探中&#xff0c;有效波和干扰波是相对的。例如&#xff0c;在反射波…...

编程新知 2026/2/2 3:20:56

（十）学生端搭建

本次旨在将之前的已完成的部分功能进行拼装到学生端&#xff0c;同时完善学生端的构建。本次工作主要包括&#xff1a; 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

编程新知 2026/2/5 4:23:32

简易版抽奖活动的设计技术方案

1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑，确保抽奖活动能够公平、公正、公开地进行，同时满足高并发访问、数据安全存储与高效处理等需求，为用户提供流畅的抽奖体验，助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

编程新知 2026/1/26 20:20:15

cf2117E

原题链接&#xff1a;https://codeforces.com/contest/2117/problem/E 题目背景&#xff1a; 给定两个数组a,b&#xff0c;可以执行多次以下操作&#xff1a;选择 i (1 < i < n - 1)&#xff0c;并设置 或&#xff0c;也可以在执行上述操作前执行一次删除任意 和 。求…...

编程新知 2026/2/4 15:29:40

镜像里切换为普通用户

如果你登录远程虚拟机默认就是 root 用户&#xff0c;但你不希望用 root 权限运行 ns-3&#xff08;这是对的&#xff0c;ns3 工具会拒绝 root&#xff09;&#xff0c;你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案&#xff1a;创建非 roo…...

编程新知 2025/9/11 11:00:29

学习STC51单片机32（芯片为STC89C52RCRC）OLED显示屏2

每日一言 今天的每一份坚持&#xff0c;都是在为未来积攒底气。 案例&#xff1a;OLED显示一个A 这边观察到一个点&#xff0c;怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 &#xff1a; 如果代码里信号切换太快&#xff08;比如 SDA 刚变&#xff0c;SCL 立刻变&#…...

编程新知 2026/2/6 0:50:24

Web 架构之 CDN 加速原理与落地实践

文章目录 一、思维导图二、正文内容&#xff08;一&#xff09;CDN 基础概念1. 定义2. 组成部分 &#xff08;二&#xff09;CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 &#xff08;三&#xff09;CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 &#xf…...

编程新知 2025/9/13 16:17:01

sipsak：SIP瑞士军刀！全参数详细教程！Kali Linux教程！

简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求&#xff0c;并检查收到的响应。它以以下模式之一…...

编程新知 2026/1/29 8:51:33

SiFli 52把Imagie图片，Font字体资源放在指定位置，编译成指定img.bin和font.bin的问题

分区配置 (ptab.json) img 属性介绍&#xff1a; img 属性指定分区存放的 image 名称&#xff0c;指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件&#xff0c;则以 proj_name:binary_name 格式指定文件名&#xff0c; proj_name 为工程 名&…...

编程新知 2026/1/23 10:51:19

A2A JS SDK 完整教程：快速入门指南

目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库&#xff…...

编程新知 2025/12/12 8:42:24