containerd安装配置
containerd基本使用命令
containerd安装
容器运行时containerd安装配置
https://blog.csdn.net/rendongxingzhe/article/details/124595415
yum list | grep containerd
containerd的本地CLI工具ctr命令
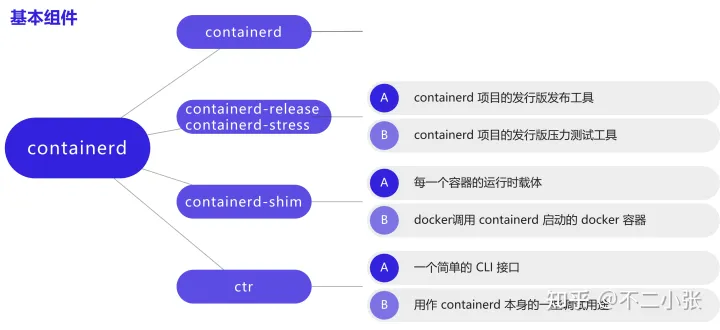
containerd的组件
containerd提供包括容器的运行、测试、发布和接口调用的工具。
containerd和k8s的关系
kubelet通过grpc协议和containerd交互。k8s规定了这个交互的规范,这就是大名鼎鼎的CRI。这里我们理解CRI为一个k8s定义的接口。它定义在 k8s.io/cri-api 中。只要实现了这套规范,就可以成为k8s的容器运行时。
Containerd 创建一个容器时会创建一个containerd-shim进程,然后container-shim进程创建业务进程。
对于k8s中的pod,可以通过containerd创建一个pause 容器,然后创建业务容器,这两个容器共享特定的namespace即可
docker-containerd的作用
1.创建容器记录的metadata
2.请求 containerd 的 task 模块,task 模块会在 runtime 中创建 task 实例,分别会加入 task list, 监控 cgroup 等操作
3.每个 task 实例则调用 shim 去创建container
Containerd的运行优势
- container和docker不同,containerd重点是继承在大规模的系统中,例如kubernetes,而不是面向开发者,让开发者使用,更多的是容器运行时的概念,承载容器运行。
- 官方提供sdk,可以在工程中实现镜像、容器得全部操作。
- 从k8s的角度看,可以选择 containerd 或 docker 作为运行时组件:其中 containerd 调用链更短,组件更少,更稳定,占用节点资源更少。
- containerd 相比于docker 多了 namespace 概念,每个 image 和 container 都会在各自的namespace下可见。
Containerd 启动流程
Docker和 Containerd 的区别

相关文章:

containerd安装配置
containerd基本使用命令 containerd安装 容器运行时containerd安装配置 https://blog.csdn.net/rendongxingzhe/article/details/124595415 yum list | grep containerd containerd的本地CLI工具ctr命令 containerd的组件 containerd提供包括容器的运行、测试、发布和接口…...
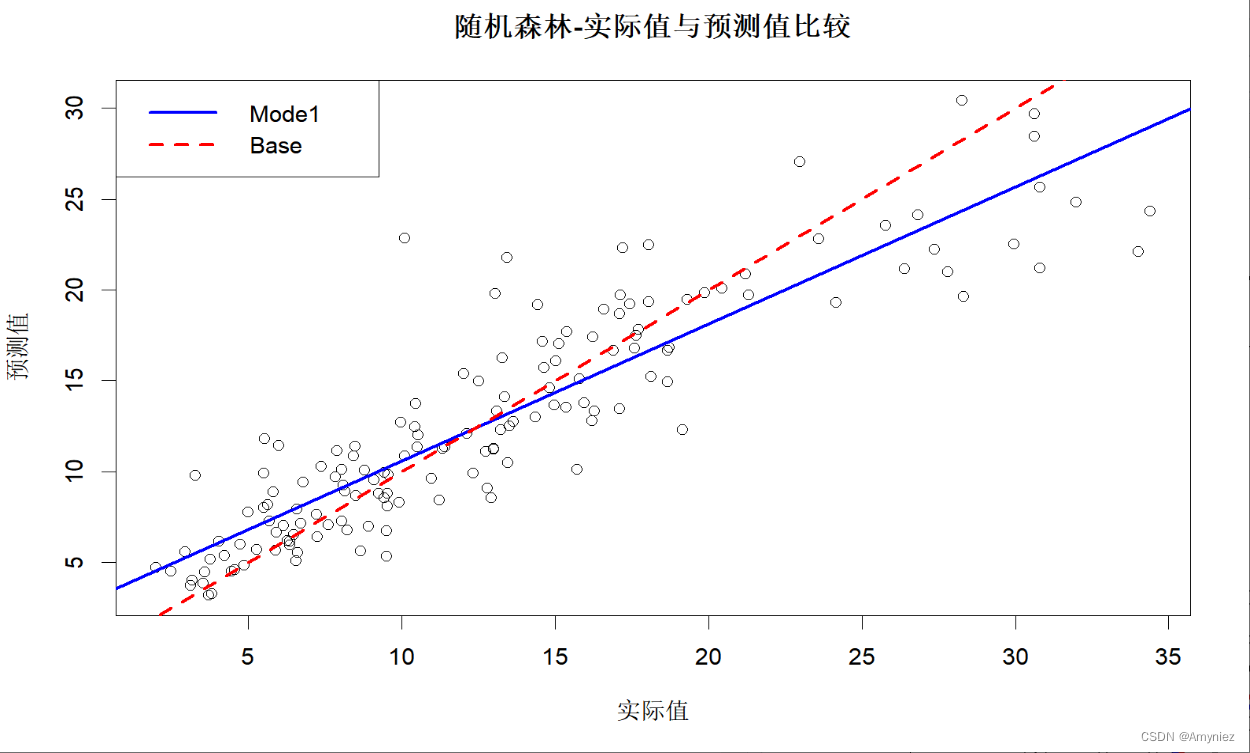
随机森林算法(Random Forest)R语言实现
随机森林1. 使用Boston数据集进行随机森林模型构建2. 数据集划分3.构建自变量与因变量之间的公式4. 模型训练5. 寻找合适的ntree6. 查看变量重要性并绘图展示7. 偏依赖图:Partial Dependence Plot(PDP图)8. 训练集预测结果1. 使用Boston数据集进行随机森…...
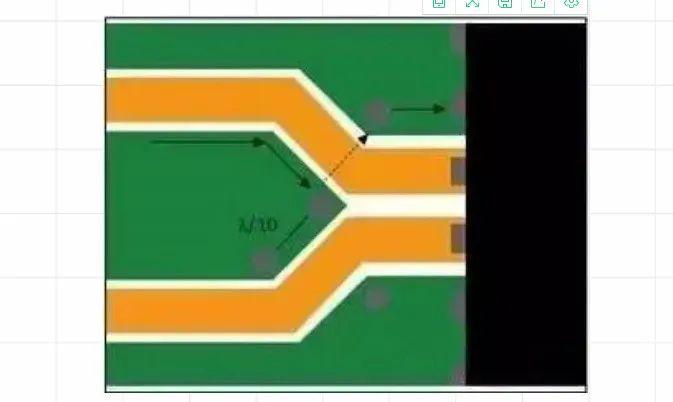
干货 | 八条“黄金规则”解决RF电路寄生信号
PART 01 接地通孔应位于接地参考层开关处流经所布线路的所有电流都有相等的回流。耦合策略固然很多,不过回流通常流经相邻的接地层或与信号线路并行布置的接地。在参考层继续时,所有耦合都仅限于传输线路,一切都非常正常。不过,如…...
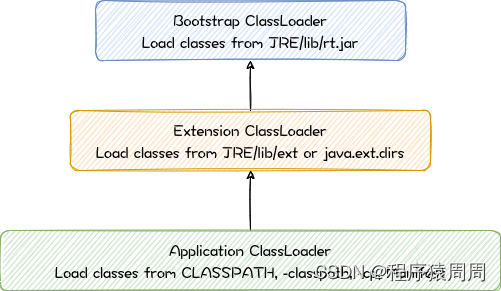
Java虚拟机之类加载学习总结
文章目录1 什么是类加载1.1 类加载的应用1.2 类加载过程1.3 类的验证1.4 类初始化顺序2 类加载时机3 类加载器3.1 类加载分类3.2 双亲委派3.3 自定义类加载器3.4 类加载器的命名空间4 打破双亲委派4.1 线程上下文类加载器4.2 自定义类加载器5 类的卸载1 什么是类加载 Java 虚拟…...

基于 vue3、vite、antdv、css 变量实现在线主题色切换
1、前言动态切换主题是一个很常见的需求. 实现方案也有很多, 如:编译多套 css 文件, 然后切换类名(需要预设主题, 不够灵活)less 在线编译(不兼容 ie, 性能较差)css 变量(不兼容 ie)但是这些基本都是针对 vue2 的, 我在网上并没有找到比较完整的解决 vue3 换肤的方案, 大多只处…...

“笨办法”学Python 3 ——练习 44 继承和组合
练习44 继承和组合 永远记住这一点:继承的大多数用法都可以用组合(composition)来简化或替换。并且无论如何都要避免多重继承。 内容提要: 1. 什么是继承? (1)隐式继承 (2&#x…...

绕过安全狗拦截的SQL注入
目录 靶场环境及中间件 知识补充 判断存在注入 整形get类注入 字符型GET注入...

JAVA练习62-无重复字符的最长子串、最长回文子串
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、题目1-无重复字符的最长子串 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 二、题目2-最长回文子串 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总…...

【JavaWeb】复习重点内容
✅✅作者主页:🔗孙不坚1208的博客 🔥🔥精选专栏:🔗JavaWeb从入门到精通(持续更新中) 📋📋 本文摘要:本篇文章主要分享JavaWeb的学习重点内容。 &a…...

基于粒子群改进的灰色神经网络的时间序列预测,PSO-GNN模型,神经网络案例之20
目标 灰色模型原理 神经网络原理 灰色神经网络原理 粒子群算法的原理 粒子群改进灰色神经网络原理 粒子群改进灰色神经网络的代码实现 效果图 结果分析 展望 灰色模型 基本思想是用原始数据组成原始序列(0),经累加生成法生成序列(1),它可以弱化原始数据的随机性,使其呈现…...
Java中的反射使用
1、获取Class对象的三种方式 1、对象调用Object类的getClass()方法(对象.getClass()) 2、调用类的class属性(类名.class) 3、调用Class类的静态方法(Class.forName(“包名.类名”))常用 Student类 package…...

urho3d工具
AssetImporter 加载开放资源导入库支持的各种三维格式(http://assimp.sourceforge.net/)并保存Urho3D模型、动画、材质和场景文件。有关支持的格式列表,请参阅http://assimp.sourceforge.net/main_features_formats.html. Blender的另一种导出路径是使用Urho3D插件…...
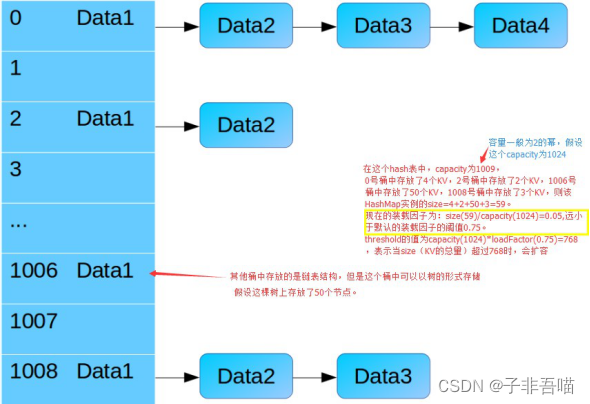
HashMap数据结构
HashMap概述 HashMap是基于哈希表的Map接口实现的,它存储的是内容是键值对<key,value>映射。此类不保证映 射的顺序,假定哈希函数将元素适当的分布在各桶之间,可为基本操作(get和put)提供稳定的性能。 HashMap在JDK1.8以前数据结构和存…...

BFC的含义以及应用
什么是BFC? BFC全称是Block Formatting context,翻译过来就是块级格式化上下文。简单来说,BFC是一个完全独立的空间。让空间里的子元素不会影响到外面的布局。😃😃😃 如何触发BFC呢? mdn给了如下方式&a…...

电脑技巧:分享8个Win11系统必备小技巧
目录 1、让任务栏显示“右键菜单” 2、任务栏置顶 3、还原经典右键菜单 4、Win11版任务管理器 5、新版AltTab 6、开始菜单不再卡 7、为Edge浏览器添加云母效果 8、自动切换日/夜模式 Win11在很多地方都做了调整,但由于涉及到诸多旧有习惯,再加上…...
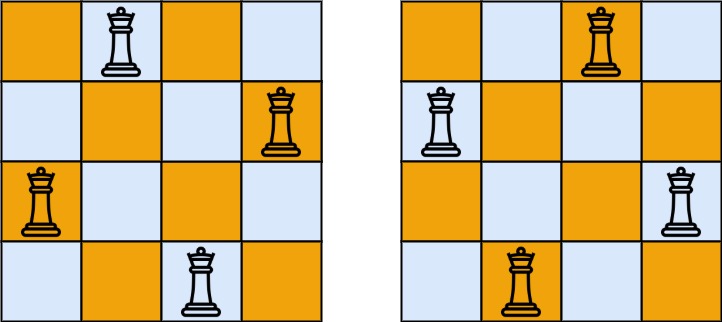
C/C++每日一练(20230226)
目录 17. 电话号码的字母组合 37. 解数独 51. N 皇后 52. N皇后 II 89. 格雷编码 90. 子集 II 17. 电话号码的字母组合 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电…...

Vue 3第二章:Vite文件目录结构及SFC语法
文章目录1. Vite 文件目录结构2. Vue3 SFC 语法规范介绍1. Vite 文件目录结构 Vue3 并没有强制规定文件目录结构,开发者可以按照自己喜欢的方式组织代码。不过,通常情况下,我们会按照以下方式组织文件目录: ├── public │ …...

Leetcode 剑指 Offer II 016. 不含重复字符的最长子字符串
题目难度: 中等 原题链接 今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~ 题目描述 给定一个字符串 s ,请你找出其中不含有重复字符的最长…...

TCP 的演化史-sack 与 reordering metric
就着 TCP 本身说事,而不是高谈阔论关于它是如何不合时宜,然后摆出一个更务虚的更新。 从一个 case 开始。 按照现在 Linux TCP(遵守 RFC) 实现,以下是一个将会导致 reordering 更新的 sack 序列: 考虑一种情况,这两个…...

【Spring6】| Spring的入门程序、集成Log4j2日志框架
目录 一:Spring的入门程序 1. Spring的下载 2. Spring的jar文件 3. 第一个Spring程序 4. 第一个Spring程序详细剖析 5. Spring6启用Log4j2日志框架 一:Spring的入门程序 1. Spring的下载 官网地址:https://spring.io/ 官网地址&…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
