华为OD机考算法题:矩阵最大值
题目部分
| 题目 | 矩阵最大值 |
| 难度 | 难 |
| 题目说明 | 给定一个仅包含 0 和 1 的 N*N 二维矩阵,请计算二维矩阵的最大值,计算规则如下: 1. 每行元素按下标顺序组成一个二进制数(下标越大越排在低位),二进制数的值就是该行的值。矩阵各行值之和为矩阵的值。 2. 允许通过向左或向右整体循环移动每行元素来改变各元素在行中的位置。 比如: [1,0,1,1,1] 向右整体循环移动 2 位变为 [1,1,1,0,1],二进制数为 11101,值为 29。 [1,0,1,1,1] 向左整体循环移动 2 位变为 [1,1,1,1,0],二进制数为 11110,值为 30。 |
| 输入描述 | 1. 输入的第一行为正整数,记录了 N 的大小,0 < N <= 20。 2. 输入的第 2 到 N+1 行为二维矩阵信息,行内元素边角逗号分隔。 |
| 输出描述 | 矩阵各行之和的最大值。 |
| 补充说明 | 无 |
| ------------------------------------------------------ | |
| 示例 | |
| 示例1 | |
| 输入 | 5 1,0,0,0,1 0,0,0,1,1 0,1,0,1,0 1,0,0,1,1 1,0,1,0,1 |
| 输出 | 122 |
| 说明 | 第一行向右整体循环移动 1 位,得到本行的最大值 [1,1,0,0,0],二进制值为 11000,十进制值为 24。 第二行向右整体循环移动 2 位,得到本行的最大值 [1,1,0,0,0],二进制值为 11000,十进制值为 24。 第三行向左整体循环移动 1 位,得到本行的最大值 [1,0,1,0,0],二进制值为 10100,十进制值为 20。 第四行向右整体循环移动 2 位,得到本行的最大值 [1,1,1,0,0],二进制值为 11100,十进制值为 28。 第五行向右整体循环移动 1 位,得到本行的最大值 [1,1,0,1,0],二进制值为 11010,十进制值为 26。 因此,矩阵的最大值为 122。 |
解读与分析
题目解读:
矩阵的每一行为一个二进制数字,通过左右移动,得到最大的二进制数。输出所有最大二进制数之和。
分析与思路:
1. 解析输入矩阵的每一行,并转换成对应的 10 进制数字;
2. 每一行的二进制数字每向右移动一位,相当于把这个数字(第一步中解析的数字,设为 value) 除以 2(取整),设为 valuePart1;然后再把 value % 2 的值(设为 modValue),乘以 ,设为 valuePart2,计算 valuePart1 与 valuePart2 之和即为向右移动一位之后的结果。
3. 在第 2 步获取的数字的基础上,继续右移。对于一个 N 位的二进制,向右移动 N 位之后就会回到初始值。因而,移动 (N -1) 次求出这 N 个数中的最大值即可。
4. 然后对每一行的最大值求和,并输出。
时间复杂度为 O(),空间复杂度为 O(n)。
代码实现
Java代码
import java.util.Scanner;
import java.util.List;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;/*** 支持优先级的队列* * @since 2023.10.26* @version 0.1* @author Frank**/
public class MatrixMaxValue {public static void main(String[] args) {Scanner sc = new Scanner(System.in);while (sc.hasNext()) {String input = sc.nextLine();int count = Integer.parseInt( input );int maxValue = 0;for( int i = 0; i < count; i ++ ){input = sc.nextLine();maxValue += getMaxValueEachLine( count, input );}System.out.println( maxValue );}}private static int getMaxValueEachLine( int count, String input ){int sourceValue = parseStringValue( input );int maxValue = sourceValue;int curValue = sourceValue;// 右移 n - 1 次,求最大值for( int i = 0; i < count - 1; i ++ ){ int partValue1 = curValue / 2;int partValue2 = (int) Math.round ( ( curValue % 2 ) * Math.pow( 2 , count - 1) ); // 使用round避免误差,不会越界curValue = partValue1 + partValue2;if( curValue > maxValue ){maxValue = curValue;}}return maxValue;}private static int parseStringValue( String input ){int ret = 0;String[] binaryArr = input.split( "," );for( int i = 0; i < binaryArr.length; i ++ ){ret *= 2;ret += Integer.parseInt( binaryArr[i] );}return ret;}
}在以上 Java 代码中,Math.pow() 函数返回的是浮点数,为了避免浮点数计算时出现误差(大概率应该不会出现误差),为了保证程序的正确性,最后使用了 Math.round() 函数。
Math.round() 返回 long 型数字,为了避免数据类型不匹配,使用强制数据类型转换。因为 N 的最大值是 20,最大值 ,比
稍大,此时不会越界。
JavaScript代码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void async function() {while (line = await readline()) {var count = parseInt( line );var maxValue = 0;for (var i = 0; i < count; i++) {line = await readline()maxValue += getMaxValueEachLine(count, line );}console.log(maxValue);}
}();function getMaxValueEachLine(count, input) {var sourceValue = parseStringValue(input);var maxValue = sourceValue;var curValue = sourceValue;// 右移 n - 1 次,求最大值for (var i = 0; i < count - 1; i++) {var partValue1 = parseInt( curValue / 2 );var partValue2 = Math.round((curValue % 2) * Math.pow(2, count - 1)); // 使用round,避免误差,不会越界curValue = partValue1 + partValue2;if (curValue > maxValue) {maxValue = curValue;}}return maxValue;
}function parseStringValue(input) {var ret = 0;var binaryArr = input.split(",");for (var i = 0; i < binaryArr.length; i++) {ret *= 2;ret += parseInt(binaryArr[i]);}return ret;
}(完)
相关文章:
华为OD机考算法题:矩阵最大值
题目部分 题目矩阵最大值难度难题目说明给定一个仅包含 0 和 1 的 N*N 二维矩阵,请计算二维矩阵的最大值,计算规则如下: 1. 每行元素按下标顺序组成一个二进制数(下标越大越排在低位),二进制数的值就是该行…...
【Javascript】函数之形参与实参
function c(a,b){return ab;}var sumc(3,4);console.log(sum);a,b为形参 3,4为实参 形参和实参是⼀⼀对应的数量可以不对应参数的类型不确定函数可以设置默认参数实参可以是字⾯量也可以是变量...

PAT 乙级1090危险品装箱
题目: 集装箱运输货物时,我们必须特别小心,不能把不相容的货物装在一只箱子里。比如氧化剂绝对不能跟易燃液体同箱,否则很容易造成爆炸。 本题给定一张不相容物品的清单,需要你检查每一张集装箱货品清单,…...
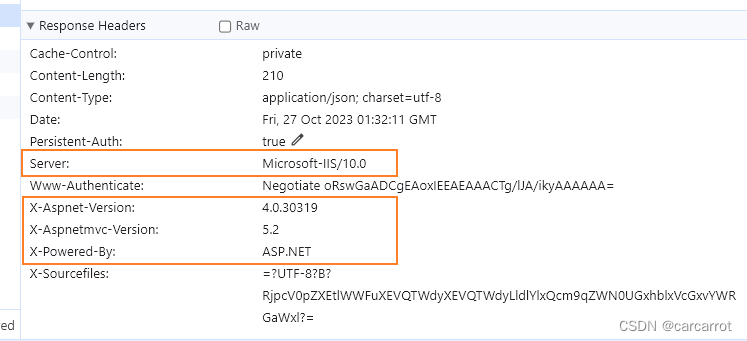
Response Header中不暴露Server(IIS)版本、ASP.NET及相关版本等信息
ASP MVC开发的Web默认情况下会在请求的回应中暴露Server、X-AspNet-Version、X-AspNetMvc-Version、X-Powered-By等相关服务端信息,公开这些敏感信息会存在一定的安全风险。 X-SourceFiles标头用于被IIS / IIS Express中某些调试模块理解,它包含到磁盘上…...
测试C#调用Vlc.DotNet组件播放视频
除了Windows Media Player组件,在百度上搜索到还有不少文章介绍采用Vlc.DotNet组件播放视频,关于Vlc.DotNet的详细介绍见参考文献1,本文学习Vlc.DotNet的基本用法。 VS2022中新建基于.net core的winform程序,在Nuget包管理器中…...
)
JS的事件委托(Event Delegation)
✨ 事件委托(Event Delegation)及其优势和缺点 🎃 什么是事件委托 事件委托是一种在JavaScript中处理事件的技术。它利用了事件的冒泡机制,将事件处理程序绑定到它们的共同祖先元素上,而不是直接绑定到每个子元素上。…...

selenium+python自动化安装驱动 碰到的问题
刚开始使用谷歌驱动,我的谷歌浏览器版本是最新版下载驱动地址,访问不了。 Chrome for Testing availability只能使用火狐驱动,我这里的火狐版本也是最新版119.0 查找全网找到驱动geckodriver下载地址 https://mirrors.huaweicloud.com/ge…...
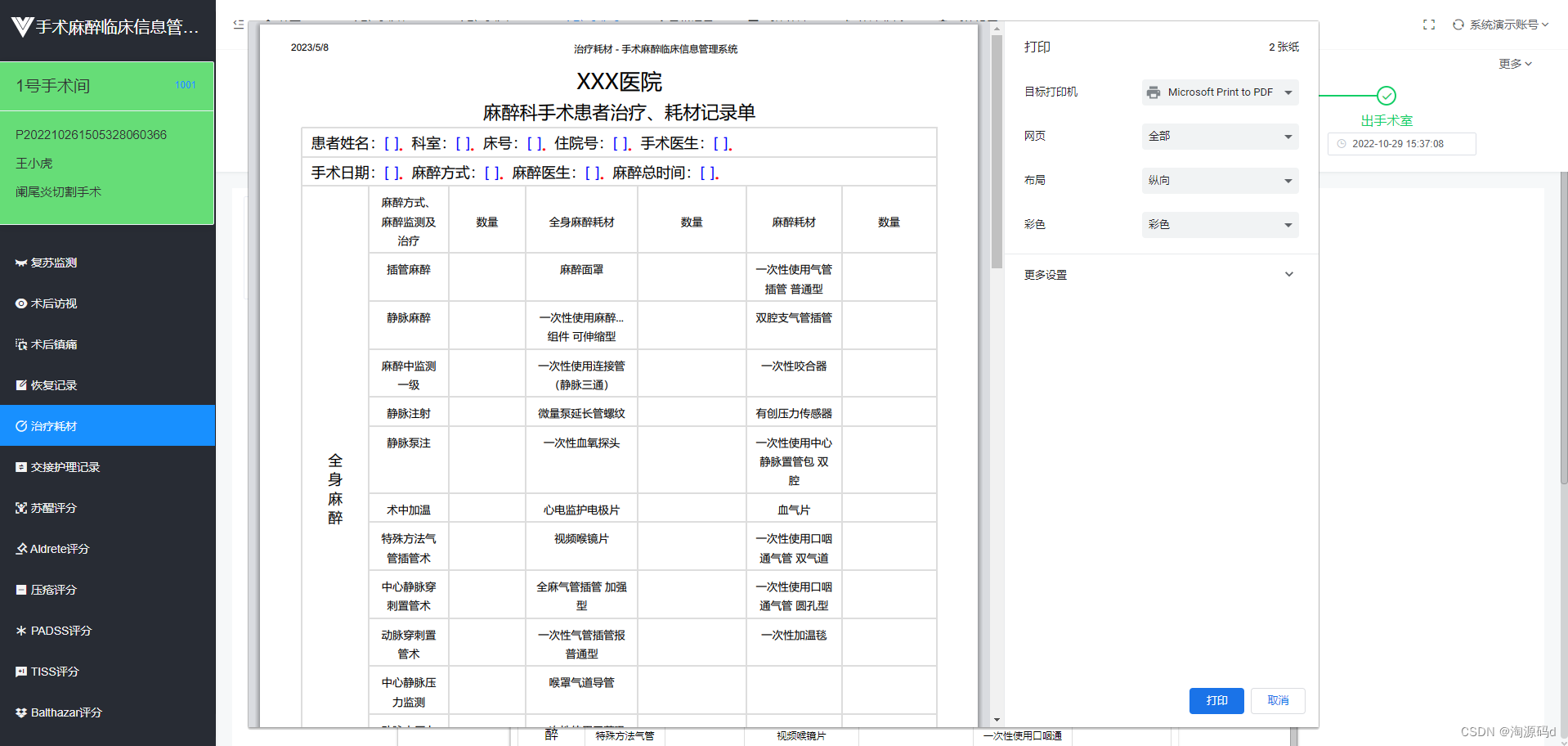
laravel+vue2 element 一套项目级医院手术麻醉信息系统源码
手术麻醉临床信息系统源码,PHPmysqllaravelvue2 手术麻醉临床信息系统,采用计算机和通信技术,实现监护仪、麻醉机、输液泵等设备输出数据的自动采集,采集的数据能够如实准确地反映患者生命体征参数的变化,并实现信息高…...

GEE——使用MODIS GPP和LAI数据进行一元线性回归计算和R2分析
使用两种方法计算一元线性回归,一种使用GEE本身自带的函数,另一种使用自己编写代码的方式进行,对比两者结果的差异。 简介 一元线性趋势分析是指利用一元线性回归模型来分析一组数据的趋势性。在一元线性回归模型中,我们假设自变量(x)和因变量(y)之间存在一定的线性关…...
[论文阅读]Point Density-Aware Voxels for LiDAR 3D Object Detection(PDV)
PDV Point Density-Aware Voxels for LiDAR 3D Object Detection 论文网址:PDV 论文代码:PDV 简读论文 摘要 LiDAR 已成为自动驾驶中主要的 3D 目标检测传感器之一。然而,激光雷达的发散点模式随着距离的增加而导致采样点云不均匀&#x…...
自动化学报格式 Overleaf 在线使用 【2023最新教程】
自动化学报格式 Overleaf 在线使用 摘要 2023年10月26日19:28:17(云南昆明) 今天课程老师要我们期末提交一篇论文,以自动化学报格式提交。因此,去官网发现只有 latex 格式,下载下来发现各种格式不兼容;由于…...

掌握CSS动画技巧:打造引人注目的页面过渡效果!
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 ⭐ 专栏简介 📘 文章引言 一…...

薛定谔的猫重出江湖?法国初创公司AliceBob研发猫态量子比特
总部位于巴黎的初创公司Alice&Bob使用超导芯片的两个相反的量子态(他们称之为“猫态量子比特”芯片)来帮助开发量子计算的不同自旋方式。(图片来源:网络) 有的人认为,构建量子计算机的模块模仿了著名的…...

18亿欧元大动作,法国瞄准实现量子飞跃
Quobly 正在开发一种容错量子处理器(图片来源:网络) 2021年1月,马克龙总统宣布了法国国家量子计算计划,并将为该技术投入高达18亿欧元。 “量子战略至关重要,”马克龙在量子研究中心巴黎萨克雷大学宣布该…...
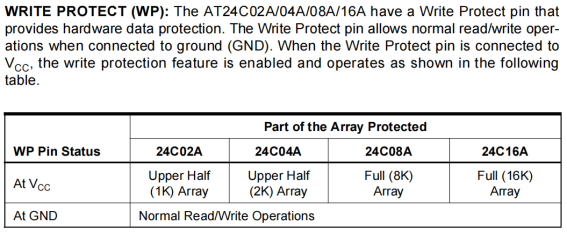
写保护设置——三、I2C EEPROM
三、I2C EEPROM I2C通讯的EEPROM只有硬保护,没有软保护。 以AT24C01A/02/04/16型EEPROM和AT24C02A/04A/08A/16A型EEPROM为例,管脚定义和写保护WP功能分别如下。 (1)AT24C01A/02/04/16型EEPROM 规格书: AT24C01A/02…...
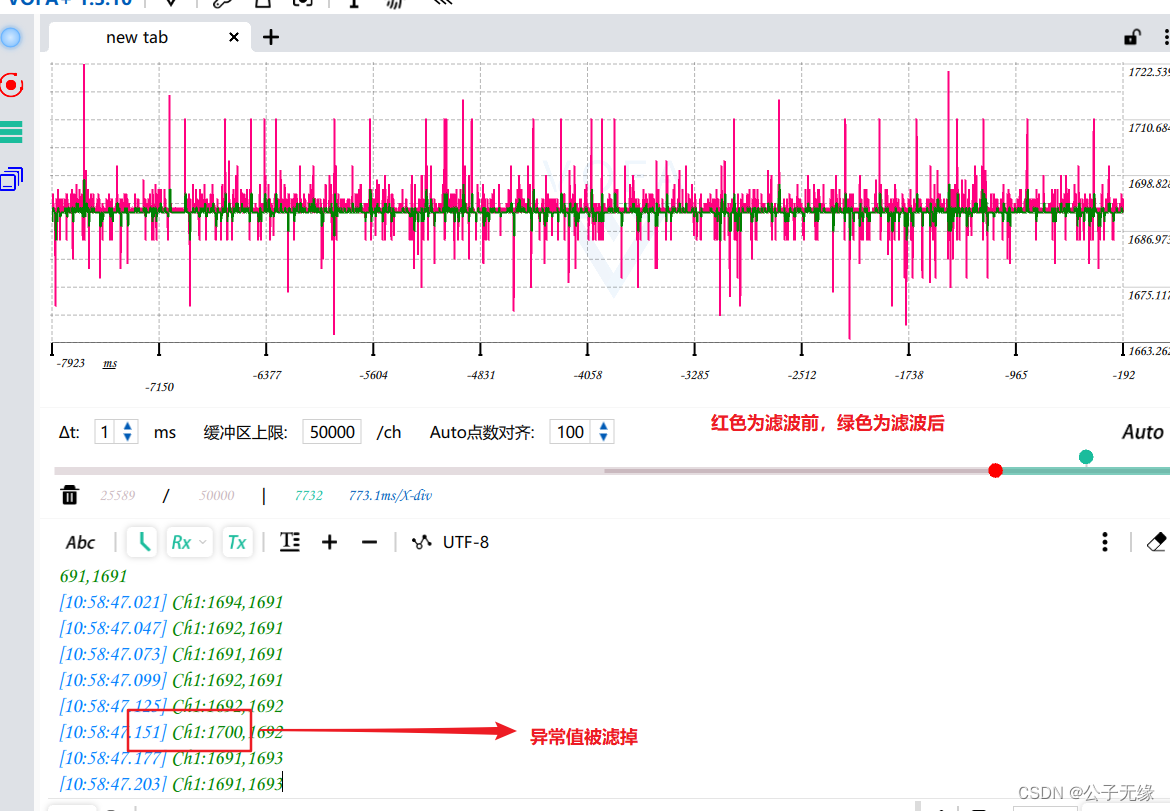
【嵌入式】HC32F07X ADC采样及软件滤波
目录 一 背景说明 二 原理分析 三 电压采样 四 软件滤波 一 背景说明 使用小华(华大)的MCU HC32F07X实现四个通道的 0-5V 电压采样,并对采样结果进行滤波处理。 二 原理分析 【1】ADC原理说明: 单片机是数字芯片,…...

VSCode snippets
生成工具:https://snippet-generator.app/ VSCode snippets:https://code.visualstudio.com/docs/editor/userdefinedsnippets#/ VS Code 中的 Snippets 是一种快捷方式,可以帮助你更快地编写代码。你可以创建自己的 Snippets,也…...
openEuler 22.03 LTS 环境使用 Docker Compose 一键部署 JumpServer (all-in-one 模式)
环境回顾 上一篇文章中,我们讲解了 openEuler 22.03 LTS 安装 Docker CE 和 Dcoker Compose,部署的软件环境版本分别如下: OS 系统:openEuler 22.03 LTS(openEuler-22.03-LTS-x86_64-dvd.iso)Docker Engine:Docker C…...

宏电5G RedCap工业智能网关获首个中国移动5G物联网开放实验室5G及轻量化产品能力认证
10月21日,2023世界物联网博览会——中国移动物联网开发者大会暨物联网产业论坛在无锡圆满举行。宏电股份参与中国移动5G物联网开放实验室5G及轻量化产品能力认证成果授牌仪式,并获得认证证书。 此次认证主要对产品功能、产品性能、RedCap网络兼容性进行测…...
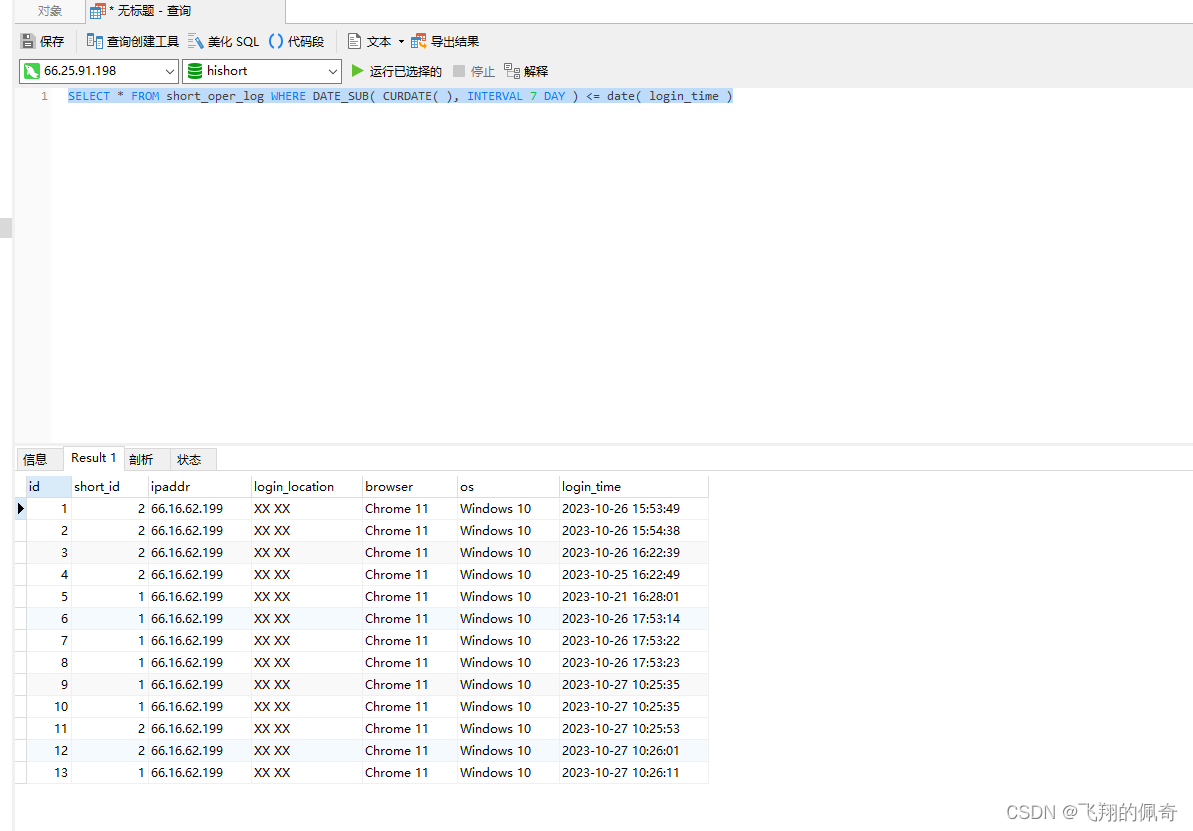
MySQL查询今日、昨日、最近七天的数据
查询今日数据 sql语句: SELECT * FROM short_oper_log WHERE to_days(login_time) to_days(now());运行结果: 查询昨日数据 sql语句: SELECT * FROM short_oper_log WHERE DATEDIFF(login_time,NOW()) -1;运行结果: 额外…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...
