统计学习方法 支持向量机（下）

统计学习方法 支持向量机（下）

学习李航的《统计学习方法》时，关于支持向量机的相关笔记。

非线性支持向量机与和核函数

核技巧

非线性分类问题：前面提到的两种 SVM 都是线性的。但有时分类问题是非线性的，需要 ${\mathbb{R}}^n$ 中的一个超曲面将正负类分开。此时我们可以使用核技巧，对训练实例进行非线性变换，映射过后变成了线性问题，就可以使用原来的方法求解：

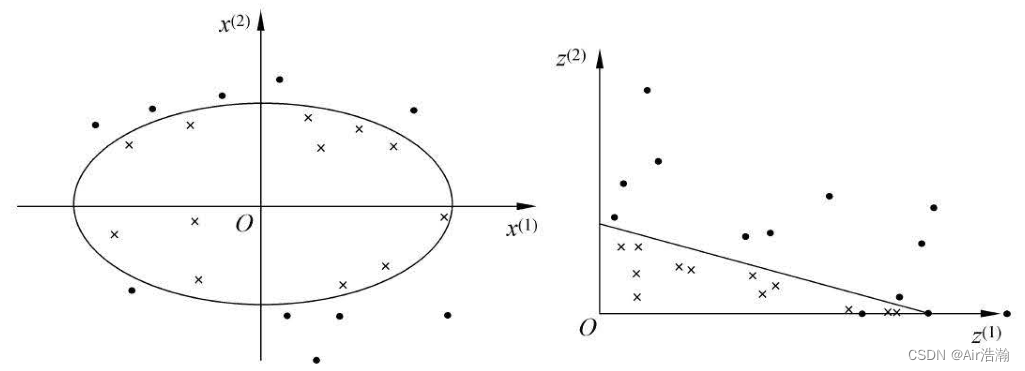
希尔伯特空间：希尔伯特空间是一个向量空间，它具有内积结构、完备性，通常是无限维度的，用于处理向量、函数或序列的数学空间。

• 内积结构允许定义向量之间的夹角和长度；
• 完备性表示空间中的柯西序列都有极限；

核函数：设 $\mathcal{X}$ 是输入空间（欧氏空间 ${\mathbb{R}}^n$ 的子集或离散集合），又设 $\mathcal{H}$ 为特征空间（希尔伯特空间），如果存在一个从 $\mathcal{X}$ 到 $\mathcal{H}$ 的映射：
$$\varphi (x):\mathcal{X}\to \mathcal{H}$$
函数 $K(x,z)$ 代表映射后的内积函数，即对所有的 $x$ ，$z\in \mathcal{X}$ ，满足条件：
$$K(x,z)=\varphi (x)\cdot \varphi (z)$$
则称 $K(x,z)$ 为核函数，$\varphi (x)$ 为映射函数。我们往往不需要直接定义 $\varphi (x)$ 核特征空间，只需要定义满足条件的 $K(x,z)$ （满足线性性、对称性和正定性），就可以把训练实例映射到某一个高维空间，就有可能使得数据集变为线性的。

核函数在支持向量机中的应用：我们所要求解的对偶问题为：
$$W(\alpha )=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^N{\alpha }_i$$
并且最终得到的分离超平面为：
$$f(x)=\text{sign}\left(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x)+b^{\ast }\right)$$
也就是说，所有训练实例 $x_i$ 在算法中都以内积的形式出现，因此我们可以直接定义核函数 $K(x,z)$ ，将问题转化为：
$$W(\alpha )=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i$$
超平面的方程可以变为：
$$f(x)=\text{sign}\left(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x)+b^{\ast }\right)$$
核函数的选择往往是基于领域知识、经验和实验验证的。

正定核

核函数代表内积运算，需要满足线性性、对称性和正定性。通常所说的核函数就是正定核函数。因此，对于一个函数 $K(x,z)$ 是否能被用作核函数，需要满足以下条件：

Th 7.5（正定核函数的充要条件）：设 $K:\mathcal{X}\times \mathcal{X}\to \mathbb{R}$ 是对称函数，则 $K(x,z)$ 为正定核函数的充分必要条件是：对任意 $x_i\in \mathcal{X}$ （$i=1,2,\cdots ,m$） ，$K(x,z)$ 对应的 Gram 矩阵：
$$K=[K(x_i,x_j){]}_{m\times m}$$
是半正定矩阵。

证明必要性：由于 $K(x,z)$ 是 $\mathcal{X}\times \mathcal{X}$ 上的正定核，所以存在从 $\mathcal{X}$ 到希尔伯特空间 $\mathcal{H}$ 的映射 $\varphi (x)$ ，使得：
$$K(x,z)=\varphi (x)\cdot \varphi (z)$$
于是，对于任意 $x_i\in \mathcal{X}$ （$i=1,2,\cdots ,m$）的 $K(x,z)$ 的 Gram 矩阵 $[K(x_i,x_j){]}_{m\times m}$ ，我们要证明该 Gram 矩阵是半正定的，只需要证明其二次型是大于等于 0 的（因为 Gram 矩阵已经对称了）。

对于任意 $c=[c_1,c_2,\cdots ,c_m{]}^{\text{T}}\in {\mathbb{R}}^m$ ，有：
$$\begin{array}{rl}{c}^{T}Kc=& \sum _{i,j=1}^m{c}_i{c}_{j}K(x_i,x_j)\\ =& \sum _{i,j=1}^m{c}_i{c}_j(\varphi (x_i)\cdot \varphi (x_j))\\ =& \left(\sum _i{c}_i\varphi (x_i)\right)\cdot \left(\sum _j{c}_j\varphi (x_j)\right)\\ =& {\Vert \sum _i{c}_i\varphi (x_i)\Vert }^2\ge 0\end{array}$$
因此该 Gram 矩阵是半正定的。

证明充分性：我们需要依照这样的 $K(x,z)$ ，去构造一个希尔伯特空间。分为三步：

1. 定义映射，构成向量空间：首先定义映射：

$$\varphi :x\to K(\cdot ,x)$$

这里 $\cdot$ 是一个占位符，表示一个参数。就是说 $\varphi$ 把 $x$ 映射成了一个函数 $K(\cdot ,x)$ ，函数的参数为 $\cdot$ ；根据这个映射，我们定义线性组合：
$$f(\cdot )=\sum _{i=1}^m{\alpha }_{i}K(\cdot ,x_i)$$
考虑由线性组合为元素构成的集合 $S$ ，它对加法和数乘运算是封闭的，所以 $S$ 构成一个向量空间。（$S$ 中的每个元素都是函数）

2. 在 $S$ 上定义内积，使其成为内积空间：对于任意 $f$ ，$g\in S$ ：

$$\begin{array}{rl}f(\cdot )=& \sum _{i=1}^m{\alpha }_{i}K(\cdot ,x_i)\\ g(\cdot )=& \sum _{j=1}^l{\beta }_{j}K(\cdot ,z_j)\end{array}$$

在 $S$ 上定义二元运算 $\ast$ ：
$$f\ast g=\sum _{i=1}^m\sum _{j=1}^l{\alpha }_i{\beta }_{j}K(x_i,z_j)$$
要证明 $\ast$ 是空间 $S$ 中的内积，需要证明线性性、对称性和正定性；线性性和对称性是挺明显的，现在证明正定性，即：
$$f\ast f\ge 0;f\ast f=0⟺f=0$$
有：
$$f\ast f=\sum _{i,j=1}^m{\alpha }_i{\alpha }_{j}K(x_i,x_j)$$
由 Gram 矩阵的半正定性得，这玩意儿 $f\ast f\ge 0$ ；对于 $f\ast f=0⟺f=0$ ，充分性显然，下面证明必要性。

首先证明 Cauchy-Shwarz 不等式，设 $f$ ，$g\in S$ ，$\lambda \in \mathbb{R}$ ，则 $f+\lambda g\in S$ ，有：
$$\begin{array}{r}(f+\lambda g)\ast f+\lambda g\ge 0\\ \Rightarrow f\ast f+2\lambda (f\ast g)+{\lambda }^2(g\ast g)\ge 0\end{array}$$
由于非负，因此判别式小于等于零，有：
$$(f\ast g{)}^2-(f\ast f)(g\ast g)\le 0$$
于是得到柯西不等式：
$$|f\ast g{|}^2\le (f\ast f)(g\ast g)$$
利用柯西不等式，我们可以得到，对于任意 $x\in \mathcal{X}$ ，有：
$$K(\cdot ,x)\ast f=\sum _{i=1}^m{\alpha }_{i}K(x,x_i)=f(x)$$
于是：
$$|f(x){|}^2=|K(\cdot ,x)\ast f{|}^2\le (K(\cdot ,x)\ast K(\cdot ,x))(f\ast f)=K(x,x)(f\ast f)$$
即：
$$|f(x){|}^2\le K(x,x)(f\ast f)$$
于是，当 $f\ast f=0$ 时，对于任意 $x$ 都有 $f(x)=0$ ，因此 $f=0$ ；

至此，我们证明了 $\ast$ 是 $S$ 中的内积运算，$S$ 是一个内积空间，我们以仍然以 $\cdot$ 表示 $\ast$ ，这是比较常用的内积符号（但是和前面的占位符不一样）。

3. 将内积空间 $S$ 完备为希尔伯特空间：由前面内积的定义可以得到范数：

$$\Vert f\Vert =\sqrt{f\cdot f}$$

因此，$S$ 是一个赋范向量空间。由泛函分析的某些理论可得，对于不完备的赋范向量空间 $S$ ，一定可以使之完备化（虽然我也不知道为啥），由此可以得到完备的赋范向量空间 $\mathcal{H}$ ，就是希尔伯特空间。

至此，我们证明了正定核的充分条件。正定核的定义也可以写为：

正定核的等价定义：设 $\mathcal{X}\subset {\mathbb{R}}^n$ ，$K(x,z)$ 是定义在 $\mathcal{X}\times \mathcal{X}$ 上的对称函数，如果对任意 $x_i\in \mathcal{X}$ ，$i=1,2,\cdots ,m$ ，$K(x,z)$ 对应的 Gram 矩阵：
$$K=[K(x_i,x_j){]}_{m\times m}$$
是半正定矩阵，则称 $K(x,z)$ 是正定核。

常用核函数

多项式核函数：对应的支持向量机是一个 $p$ 此多项式分类器：
$$K(x,z)=(x\cdot z+1{)}^p$$
分类决策函数为：
$$f(x)=\text{sign}\left(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x+1{)}^p+b^{\ast }\right)$$
高斯核函数：使用高斯径向函数（RBF）：
$$K(x,z)=\text{exp}\left(-\frac{\Vert x-z{\Vert }^2}{2{\sigma }^2}\right)$$
分类决策函数为：
$$f(x)=\text{sign}\left(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\text{exp}\left(-\frac{\Vert x-x_i{\Vert }^2}{2{\sigma }^2}\right)+b^{\ast }\right)$$

字符串核函数：定义有限字符表 $\Sigma$ ：

• 字符串 $s$ 是从 $\Sigma$ 中取出有限个字符的序列，其长度表示为 $|s|$ 。

• 两个字符串 $s$ 和 $t$ 的连接记为 $st$

• 所有长度为 $n$ 的字符串集合记作 ${\Sigma }^n$ ；

• 所有字符串的集合记作 ${\Sigma }^{\ast }=\bigcup _{i=1}^{\infty }{\Sigma }^i$ ；

给定一个下标序列 $i=(i_1,i_2,\cdots ,i_{|u|})$ ，其中 $1\le i_1<i_2<\cdots <i_{|u|}\le |s|$ ，考虑 $s$ 字符串的子串 $u=s[i]$ ，定义 $l(i)=i_{|u|}-i_1+1$ ，代表下标的跨度。若 $i$ 是连续的，则 $l(i)=|u|$ ，否则 $l(i)>|u|$ 。

设 $S$ 是长度大于等于 $n$ 的字符串的集合，设 $s\in S$ 。先建立字符串集合 $S$ 到特征空间 ${\mathcal{H}}_n={\mathbb{R}}^{|{\Sigma }^n|}$ 的映射 ${\varphi }_n(s)$ 。其中 $|{\Sigma }^n|$ 代表集合 ${\Sigma }^n$ 的基数，${\mathbb{R}}^{|{\Sigma }^n|}$ 中向量的每一维对应某个字符串 $u\in {\Sigma }^n$ 。

定义 ${\mathbb{R}}^{|{\Sigma }^n|}$ 中向量在 $u$ 维上的取值为：
$$[{\varphi }_n(s){]}_u=\sum _{i:s(i)=u}{\lambda }^{l(i)}$$
这里 $0<\lambda \le 1$ 是一个衰减参数，求和表示在 $s$ 中所有为 $u$ 的子串上进行；

例：对于英文字符串，$n=3$ ，现将 $S$ 映射到 ${\mathcal{H}}_3$ 。设 ${\mathcal{H}}_3$ 中的向量的第一维对应于字符串 asd ，则对于两个字符串 Nasdaq 和 lass das ，它们在第一维上的取值分别为：

• $[{\varphi }_3(\text{Nasdaq}){]}_{\text{asd}}={\lambda }^3$ ：因为 Nasdaq 只有一个子串为 asd ，下标为 $(2,3,4)$ ，所以 $l((2,3,4))=3$ ；
• $[{\varphi }_3(\text{lass das}){]}_{\text{asd}}=2{\lambda }^5$ ：lass das 有两个子串为 asd ，且对应的 l(i) 均为 5；

我们定义字符串 $s$ 和 $t$ 的核函数为：
$$\begin{array}{rl}{K}_n(s,t)=& \sum _{u\in {\Sigma }^n}[{\varphi }_n(s){]}_u[{\varphi }_n(t){]}_u\\ =& \sum _{u\in {\Sigma }^n}\sum _{(i,j):s(i)=t(j)=u}{\lambda }^{l(i)}{\lambda }^{l(j)}\end{array}$$
可以理解为，两个字符串共同子串越多，二者就越相似。字符串核函数可以由动态规划来快速计算。

非线性 SVM

非线性支持向量机：给定非线性分类训练集，通过核函数与软间隔最大化，或对应的对偶最优化问题，学习得到的分类决策函数：
$$f(x)=\text{sign}\left(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x,x_i)+b^{\ast }\right)$$
称为非线性支持向量机，$K(x,z)$ 是正定核函数。

算法：非线性支持向量机学习算法

• 输入：线性可分训练数据集 T = { ( x 1 , t 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\set{(x_1,t_1),(x_2,y_2),\cdots,(x_N,y_N)} T={(x1​,t1​),(x2​,y2​),⋯,(xN​,yN​)} ，其中 $x_i\in \mathcal{X}\subseteq {\mathbb{R}}^n$ ， y i ∈ Y = { 1 , − 1 } y_i\in\mathcal{Y}=\set{1,\,-1} yi​∈Y={1,−1}
• 输出：分类决策函数

1. 选取适当的核函数 $K(x,z)$ 和超参数 $C$ ，构造求解最优化问题：

$$\begin{array}{rl}\underset{\alpha }{\min }& \frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i\\ \text{s.t.}& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i\ge 0,i=1,2,\cdots ,N\end{array}$$

得到最优解 ${\alpha }^{\ast }$ ；

2. 选择 ${\alpha }^{\ast }$ 的一个正分量 ${\alpha }_j^{\ast }$ ，计算：
   $$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j)$$

3. 构造决策函数：

$$f(x)=\text{sign}\left(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x,x_i)+b^{\ast }\right)$$

当 $K(x,z)$ 是正定核函数时，该问题是凸二次规划问题，解是存在的。

序列最小最优化算法

我们在求解对偶的凸二次规划问题时，当样本量很大时， 一般的最优化算法会变得很低效：
$$\begin{array}{rl}\underset{\alpha }{\min }& \frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i\\ \text{s.t.}& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le C,i=1,2,\cdots ,N\end{array}$$
SMO（序列最小最优化）算法是一种启发式算法，思路为：

• 如果所有变量的解都满足 KKT 条件，则解就得到了；
• 否则，选取两个变量，固定其他变量，针对这两个变量构建一个二次规划问题。两个变量的二次规划问题可以直接通过解析方法求解。这个二次规划问题关于这两个变量的解应当比原来更接近原始二次规划问题的解；
• 子问题有两个变量：一个是违反 KKT 条件最严重的那个，另一个由约束条件自动确定；
• 通过不断地将原问题分解为子问题，并且求解子问题，从而迭代地达到求解原问题的目的。

注意，子问题的两个变量只有一个是自由变量，例如，假设 ${\alpha }_1$ 和 ${\alpha }_2$ 为变量，其余 $\alpha$ 固定，则可以得到：
$${\alpha }_1=-y_1\sum _{i=2}^N{\alpha }_i{y}_i$$
如果 ${\alpha }_2$ 确定，则 ${\alpha }_1$ 也随之确定。

SMO 算法包含两个部分：两个变量二次规划问题的解析解和选择变量的启发式方法。

两个变量二次规划的求解方法

两个变量二次规划问题：同样地，假设 ${\alpha }_1$ 和 ${\alpha }_2$ 为变量，其余 $\alpha$ 固定（我们将 ${\alpha }_2$ 看作自由变量），则可以得到（注意 $y_i^2=1$）：
$$\begin{array}{rl}\underset{{\alpha }_1,{\alpha }_2}{\min }& W({\alpha }_1,{\alpha }_2)=\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_2{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2\\ & -({\alpha }_1+{\alpha }_2)+y_1{\alpha }_1\sum _{i=3}^N{y}_i{\alpha }_i{K}_{i1}+y_2{\alpha }_2\sum _{i=3}^N{y}_i{\alpha }_i{K}_{i2}\\ \text{s.t.}& {\alpha }_1{y}_1+{\alpha }_2{y}_2=-\sum _{i=3}^N{y}_i{\alpha }_i=\zeta \\ & 0\le {\alpha }_i\le C,i=1,2\end{array}$$
其中 $K_{ij}=K(x_i,x_j)$ ，$\zeta$ 为常数；

约束条件：注意到 $y_i$ 只有 $\pm 1$ 的取值，因此约束有两种情况（${\alpha }_2$ 是纵坐标，${\alpha }_1$ 是横坐标）：

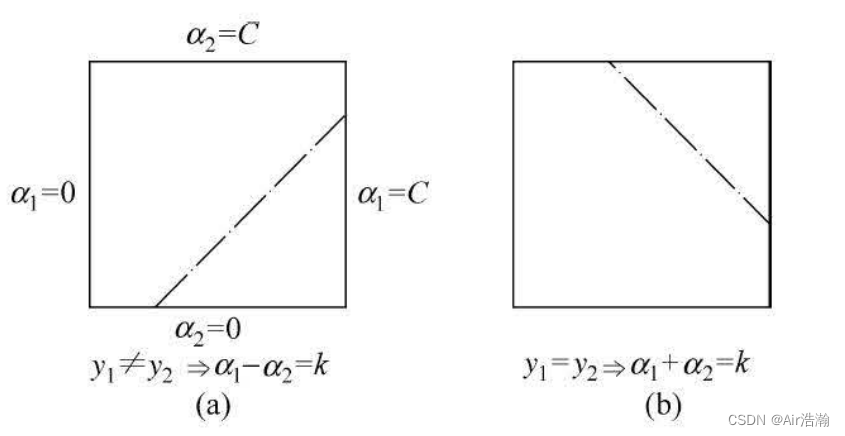
约束是 $[0,C]$ 的正方形内的一条对角线，方程为 ${\alpha }_2-{\alpha }_2^{\text{old}}+y_1{y}_2({\alpha }_1-{\alpha }_1^{\text{old}})=0$ ；

假设初始可行解为 ${\alpha }_1^{\text{old}}$ ， ${\alpha }_2^{\text{old}}$ ，最优解为 ${\alpha }_1^{\text{new}}$ ， ${\alpha }_2^{\text{new}}$ ；并且假设在沿着约束方向未经 $0\le {\alpha }_i\le C$ 剪辑时 ${\alpha }_2$ 的最优解为 ${\alpha }_2^{\text{new unc}}$ 。

最优解 ${\alpha }_2^{\text{new}}$ 的取值范围需满足条件：
$$L\le {\alpha }_2^{\text{new}}\le H$$
$L$ 和 $H$ 就是对角线段的端点，如果 $y_1\ne y_2$ ，则直线的表达式为 ${\alpha }_2={\alpha }_1+{\alpha }_2^{\text{old}}-{\alpha }_1^{\text{old}}$ ：
$$L=\max (0,{\alpha }_2^{\text{old}}-{\alpha }_1^{\text{old}}),H=\min (C,C+{\alpha }_2^{\text{old}}-{\alpha }_1^{\text{old}})$$
如果 $y_1=y_2$ ，则直线的表达式为 ${\alpha }_2=-{\alpha }_1+{\alpha }_2^{\text{old}}+{\alpha }_1^{\text{old}}$ ：
$$L=\max (0,{\alpha }_2^{\text{old}}+{\alpha }_1^{\text{old}}-C),H=\min (C,{\alpha }_2^{\text{old}}+{\alpha }_1^{\text{old}})$$
求解 ${\alpha }_2^{\text{new}}$：我们的思想是，先求得 ${\alpha }_2^{\text{new unc}}$ ，再使用 $[L,H]$ 剪辑得到 ${\alpha }_2^{\text{new}}$ ：
$${\alpha }_2^{\text{new}}=\{\begin{array}{ll}H,& {\alpha }_2^{\text{new unc}}>H\\ {\alpha }_2^{\text{new unc}},& L\le {\alpha }_2^{\text{new unc}}\le H\\ L,& {\alpha }_2^{\text{new unc}}<L\end{array}$$
而 ${\alpha }_1^{\text{new}}$ 为：
$${\alpha }_1^{\text{new}}={\alpha }_1^{\text{old}}-y_1{y}_2({\alpha }_2^{\text{new}}-{\alpha }_2^{\text{old}})$$
求解 ${\alpha }_2^{\text{new unc}}$：记：
$$g(x)=\sum _{i=1}^N{\alpha }_i^{\text{old}}{y}_{i}K(x_i,x)+b^{\text{old}}$$
其中 $b^{\text{old}}$ 是以当前迭代到的可行解 ${\alpha }^{\text{old}}$ 计算得到的 $b$ ；$g(x)$ 其实就是以当前迭代到的可行解 ${\alpha }^{\text{old}}$ 计算得到的去掉符号函数的决策函数；令：
$$E_i=g(x_i)-y_i=\left(\sum _{j=1}^N{\alpha }_j^{\text{old}}{y}_{j}K(x_j,x_i)+b^{\text{old}}\right)-y_i,i=1,2$$
再引入记号（$\Phi$ 为核函数 $K(x,z)$ 所对应的输入空间到特征空间的映射）：
$$\eta =K_{11}+K_{22}-2K_{12}=\Vert \Phi (x_1)-\Phi (x_2){\Vert }^2$$
则可以得到两个变量二次规划问题在沿着约束方向未经剪辑时 ${\alpha }_2$ 的最优解为：
$${\alpha }_2^{\text{new unc}}={\alpha }_2^{\text{old}}+\frac{y_2(E_1-E_2)}{\eta }$$
证明：引进记号（为了方便书写，去掉了 $\text{old}$ 上标。没有特殊说明都是 $\text{old}$）：
$$v_i=\sum _{j=3}^N{\alpha }_j{y}_{j}K(x_i,x_j)=g(x_i)-\sum _{j=1}^2{\alpha }_j{y}_{j}K(x_i,x_j)-b,i=1,2$$
则目标函数写成：
$$\begin{array}{rl}W({\alpha }_1,{\alpha }_2)=& \frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_2{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2\\ -& ({\alpha }_1+{\alpha }_2)+y_1{\alpha }_1\sum _{i=3}^N{y}_i{\alpha }_i{K}_{i1}+y_2{\alpha }_2\sum _{i=3}^N{y}_i{\alpha }_i{K}_{i2}\\ =& \frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_2{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2\\ -& ({\alpha }_1+{\alpha }_2)+y_1{v}_1{\alpha }_1+y_2{v}_2{\alpha }_2\end{array}$$
现在这个目标函数同时含有 ${\alpha }_1$ 和 ${\alpha }_2$ ，我们要计算 ${\alpha }_2^{\text{new unc}}$ ，因此只保留约束条件 ${\alpha }_1{y}_1+{\alpha }_2{y}_2=\zeta$ ，消去 ${\alpha }_1$ ，仅保留 ${\alpha }_2$ ：
$${\alpha }_1=y_1(\zeta -{\alpha }_2{y}_2)$$
将其带入目标函数，得到：
$$\begin{array}{rl}W({\alpha }_2)=& \frac{1}{2}{K}_{11}(\zeta -{\alpha }_2{y}_2{)}^2+\frac{1}{2}{K}_2{\alpha }_2^2+y_2{K}_{12}(\zeta -{\alpha }_2{y}_2){\alpha }_2\\ -& y_1(\zeta -{\alpha }_2{y}_2)-{\alpha }_2+v_1(\zeta -{\alpha }_2{y}_2)+y_2{v}_2{\alpha }_2\end{array}$$
现在只有一个变量了，FOC 为：
$$\begin{array}{rl}\frac{\partial W}{\partial {\alpha }_2}=& K_{11}{\alpha }_2-K_{11}\zeta y_2+K_{22}{\alpha }_2+K_{12}\zeta y_2-2K_{12}{\alpha }_2+y_1{y}_2-1-v_1{y}_2+v_2{y}_2\\ =& 0\end{array}$$
得到：
$$\begin{array}{rl}(K_{11}+K_{22}-2K_{12}){\alpha }_2=& y_2(K_{11}\zeta -K_{12}\zeta -y_1+y_2+v_1-v_2)\\ =& y_2[K_{11}\zeta -K_{12}\zeta -y_1+y_2\\ +& \left(g(x_1)-\sum _{j=1}^2{\alpha }_j{y}_j{K}_{1j}-b\right)\\ -& \left(g(x_2)-\sum _{j=1}^2{\alpha }_j{y}_j{K}_{2j}-b\right)]\\ =& y_2\left(K_{11}\zeta -K_{12}\zeta +E_1-E_2-\sum _{j=1}^2{\alpha }_j{y}_j{K}_{1j}+\sum _{j=1}^2{\alpha }_j{y}_j{K}_{2j}\right)\\ =& y_2(E_1-E_2+{\alpha }_2{y}_2(K_{11}+K_{22}-2K_{12}))\end{array}$$

• 中间带入了 $E_i=g(x_i)-y_i$ 和 $\zeta ={\alpha }_1^{\text{old}}{y}_1+{\alpha }_2^{\text{old}}{y}_2$ ；

• 注意 $K_{12}=K_{21}$ ；

再带入 $\eta =K_{11}+K_{22}-2K_{12}$ ，就能得到：
$${\alpha }_2^{\text{new unc}}={\alpha }_2^{\text{old}}+\frac{y_2(E_1-E_2)}{\eta }$$

变量的选择方法

SMO 算法在每个子问题中选择两个变量优化，其中至少一个变量时违反 KKT 条件的。

第一个变量的选择：该过程称为外层循环，选取所有训练样本中违反 KKT 条件最严重的样本点作为第一个变量 ${\alpha }_1$ 。KKT 条件为：
$$\begin{array}{r}{\alpha }_i=0⟺y_{i}g(x_1)\ge 1\\ 0<{\alpha }_i<C⟺y_{i}g(x_1)=1\\ {\alpha }_i=C⟺y_{i}g(x_1)\le 1\end{array}$$
SMO 算法往往有一个超参数为精度 $\epsilon$ ，该检查是在 $\epsilon$ 的误差范围内进行的。 外层循环先检查 $0<{\alpha }_i<C$ （间隔边界上）的样本点，再检验其他样本点；

第二个变量的选择：该过程称为内层循环，选择标准为能使得 ${\alpha }_2$ 有足够大的变化。

• ${\alpha }_2^{\text{new}}$ 是依赖于 $|E_1-E_2|$ 的，在 ${\alpha }_1$ 确定的情况下， $E_1$ 也随之确定了。所以选择一个使得 $|E_1-E_2|$ 最大的 ${\alpha }_2$ 即可；为了加速计算，可以在变量选择时提前算好所有的 $E_i$ ；
• 有时上述方法得到的 ${\alpha }_2$ 不能使得目标函数有足够的下降，可以采用启发式规则继续选择 ${\alpha }_2$ ：首先检查间隔边界上（ $0<{\alpha }_i<C$ ）的样本点作为 ${\alpha }_2$ 试用，使得目标函数有足够的下降；再试用其他样本点；最后都不行的话，放弃 ${\alpha }_1$ 并重新选择；

计算偏移量 $b$ 和差值 $E_i$ ：每次完成两个变量的优化后，就要用新的 $\alpha$ 计算 $b$ 。

当 $0<{\alpha }_1^{\text{new}}<C$ 时，由 KKT 条件可知：
$$\begin{array}{rl}b=& y_1-\sum _{i=1}^N{\alpha }_i{y}_i{K}_{1i}\\ =& y_1-\sum _{i=3}^N{\alpha }_i{y}_i{K}_{1i}-{\alpha }_1^{\text{new}}{y}_1{K}_{11}-{\alpha }_2^{\text{new}}{y}_2{K}_{12}\end{array}$$
带入 $E_1$ 得到：
$$b_1^{\text{new}}=-E_1-y_1{K}_{11}({\alpha }_1^{\text{new}}-{\alpha }_1^{\text{old}})-y_2{K}_{12}({\alpha }_2^{\text{new}}-{\alpha }_2^{\text{old}})+b^{\text{old}}$$
若 $0<{\alpha }_2^{\text{new}}<C$ ，则：
$$b_2^{\text{new}}=-E_2-y_1{K}_{12}({\alpha }_1^{\text{new}}-{\alpha }_1^{\text{old}})-y_2{K}_{22}({\alpha }_2^{\text{new}}-{\alpha }_2^{\text{old}})+b^{\text{old}}$$
对于 $E_i$ 值的更新，直接按照定义式算就可以了，但是需要用到 $b^{\text{new}}$ ：
$$E_i^{\text{new}}=\sum _{j=1}^N{y}_j{\alpha }_{i}K(x_i,x_j)+b^{\text{new}}-y_i$$
这里不一定需要从 $j=1$ 遍历到 $N$ ，因为只有支持向量的 ${\alpha }_j\ne 0$ ，所以可以维护一个支持向量的集合 $S$ ；

SMO 算法

输入：线训练数据集 T = { ( x 1 , t 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\set{(x_1,t_1),(x_2,y_2),\cdots,(x_N,y_N)} T={(x1​,t1​),(x2​,y2​),⋯,(xN​,yN​)} ，其中 $x_i\in \mathcal{X}\subseteq {\mathbb{R}}^n$ ， y i ∈ Y = { 1 , − 1 } y_i\in\mathcal{Y}=\set{1,\,-1} yi​∈Y={1,−1} ；精度 $\epsilon$ ；

输出：近似解 $\hat{\alpha }$ ；

1. 选取初值 ${\alpha }^{(0)}=0$ ，令计步数 $k=0$ ；
2. 以上述选取变量方法选取优化变量 ${\alpha }_1^{(k)}$ 和 ${\alpha }_2^{(k)}$ ，直接用解析方程得到二者最优解 ${\alpha }_1^{(k+1)}$ 和 ${\alpha }_2^{(k+1)}$ ，此时 $\alpha$ 更新为 ${\alpha }^{(k+1)}$ ；
3. 若在精度 $\epsilon$ 范围内满足停机条件（约束条件）：

$$\sum _{i=1}^N{\alpha }_i{y}_i=0,0\le {\alpha }_i\le C,i=1,2,\cdots ,N$$

和：
y i g ( x i ) { ≥ 1 , { x i ∣ α i = 0 } = 1 , { x i ∣ 0 < α i < C } ≤ 1 , { x i ∣ α i = C } y_ig(x_i)\left\{ \begin{array}{ll} \geq 1, & \set{x_i|\alpha_i=0} \\ = 1, & \set{x_i|0\lt\alpha_i\lt C} \\ \leq 1, & \set{x_i|\alpha_i=C} \\ \end{array} \right. yi​g(xi​)⎩ ⎨ ⎧​≥1,=1,≤1,​{xi​∣αi​=0}{xi​∣0<αi​<C}{xi​∣αi​=C}​
其中：
$$g(x_i)=\sum _{j=1}^N{\alpha }_j{y}_{j}K(x_i,x_j)+b$$

4. 返回 $\hat{\alpha }={\alpha }^{(k+1)}$ ；