时间、空间复杂度的例题详解
文章前言
上篇文章带大家认识了数据结构和算法的含义,以及理解了时间、空间复杂度,那么接下来来深入理解一下时间、空间复杂度。
时间复杂度实例
实例1
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
很明显可以知道是2*N+10,所以时间复杂度为O(n)。
实例2
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}
运行次数是N+M,时间复杂度为 O(N+M)
实例3
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
在这里面进行了100次循环和N没有关系,所有时间复杂度为O(1)
实例4
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character );
大家如果不了解strchr函数,可以大概看一下介绍:
strchr 函数是一个 C 标准库中的字符串函数,用于从字符串中查找指定字符的第一次出现位置,它的函数原型为:
char *strchr(const char *s, int c);
该函数的内部构造实现并不是特别复杂,它的实现可以分为以下几个步骤:
检验输入参数是否合法,若非法则返回 NULL。其中,参数 s 表示需要查找的字符串,参数 c 表示需要查找的字符。
if (s == NULL)return NULL;
遍历字符串 s,查找字符 c 的出现位置,若找到则返回该位置的指针。若未找到则返回 NULL。
while (*s != '\0') {if (*s == (char)c)return (char *)s;s++;
}
return NULL;
上述代码使用了一个 while 循环,遍历字符串中的每个字符,检查当前字符是否等于指定字符 c。一旦找到了第一次出现 c 的位置,就立即返回该位置的指针。如果遍历完整个字符串后仍未找到指定字符,则最终返回 NULL。
综上所述,strchr 函数的内部构造并不复杂,主要是遍历字符串查找目标字符的过程。需要注意的是,由于该函数返回的是指针类型,因此需要进行类型转换。
所以,我们可以很容易的根据时间复杂度的定义:基本操作执行最好1次,最坏N次,时间复杂度一般看最坏,时间复杂度为 O(N)。
实例5
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
基本操作执行最好N次,最坏执行了(N*(N+1)/2次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为 O(N^2)。
实例6
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}
我们可以知道这是一个二分查找,二分查找是一个很厉害的算法,他的效率特别高。 基本操作执行最好1次,最坏O(logN)次,时间复杂度为 O(logN) (ps:logN在算法分析中表示是底数为2,对数为N。有些地方会写成lgN。)
实例7
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}
可以很简单的知道执行次数是N+1次,那么时间复杂度为O(n)。
实例8
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
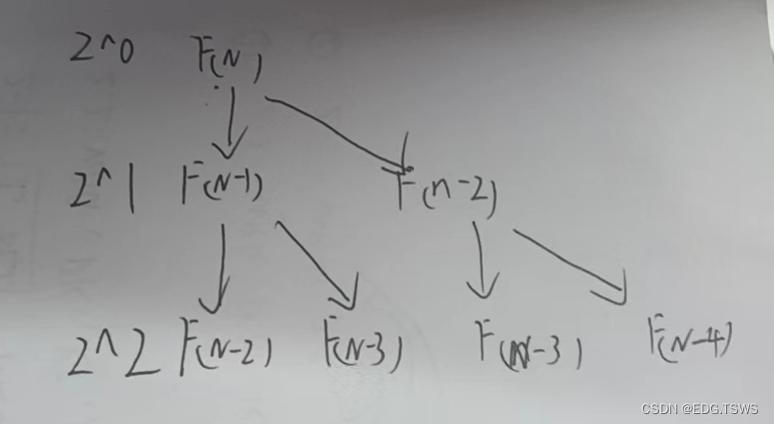


大概也就是(1/2)*2N-1,所以时间复杂度就为O(2^N)。
空间复杂度实例
实例1
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
仅使用了常数个额外空间,所以空间复杂度为O(1)。
实例2
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}
该代码动态开辟了N个空间,所以空间复杂度为O(N)。
实例3
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}
递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)。
根据时间、空间复杂度解题
消失的数字
问题描述:
数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗?
这里给大家把链接奉上,可以先挑战一下试试。
https://leetcode-cn.com/problems/missing-number-lcci/
思路分析:
首先很简单的做法是暴力遍历,但是效率不够高,可能会超时,所以这种做法可行只要不出问题都可以作出来,就不再过多赘述。
思路一:
从0到n,丢失了一个数字,我们可以把从0到n的数字先全部加起来,之后用这个值减去所有的数字,就可以知道这个丢失的数字是多少了。
int missingNumber(int* nums, int numsSize) {int N = numsSize;//用N来记录方便代码书写int sum = ((0 + N) * (N + 1)) / 2;//等茶树列前n项和for (int i = 0; i < N; i++)//减值循环{sum = sum - nums[i];}return sum;//返回值为sum即为丢失的数字。
}
该题解代码时间复杂度为O(N),空间复杂度为O(1)。
在这里是可以通过的,我们具体解释看注释。
思路二:我们之前学过异或符号,得到了一个结论相同为0,相异为1。那么我们就可以得到两个相同的数字异或起来得到的值就是0。0异或任何数字又都是该数字,那么我们就可以让0去异或从0到n,再去异或所有的数,最后得到的值就是丢失的那个数字。
int missingNumber(int* nums, int numsSize)
{int N = numsSize;//N来记录方便代码书写int F = 0;//定义F为0,用来异或for (int i = 0; i <= N; i++)//异或从0到n的所有数字循环{F ^= i;}for (int i = 0; i < N; i++)//再去异或所有数字的循环{F ^= nums[i];}return F;//得到的F即为丢失的数字返回即可。
}
该题解代码同样是时间复杂度为O(N),空间复杂度为O(1)。
可以看到在这里是通过的,具体解释请看代码。
移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
链接给大家奉上可以先尝试一下:
https://leetcode.cn/problems/remove-element/
题解思路:已经规定不能使用额外空间,那么我们可以用双指针的方法来解这道题目。
int removeElement(int* nums, int numsSize, int val){int src=0;//快指针(下标)int dst=0;//慢指针(下标)while(src<numsSize)//移除循环{if(nums[src]!=val)//快指针遍历,若不等于移除值,将快指针指向值赋给慢指针{nums[dst]=nums[src];dst++;src++;}else//除不相等情况,为相等情况,快指针直接遍历过去{src++;}}return dst;//返回新数组长度。
}
在这里,时间复杂度是O(N),空间复杂度为O(1)。
具体代码解释请看注释。
删除有序数组中的重复项
给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
更改数组 nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
链接奉上:
https://leetcode.cn/problems/remove-duplicates-from-sorted-array/description/
int removeDuplicates(int* nums, int numsSize) {int j=1;//快指针遍历int i=1;//慢指针记录for(j=1;j<numsSize;j++)//移除循环{if(nums[j]!=nums[i-1])//快指针遍历值不等于前一项慢指针记录值时//将该快指针指向值赋值给慢指针当前项值//相等情况快指针直接遍历过去{nums[i]=nums[j];i++;}}return i;
}
在这里同样用双指针方法,时间复杂度为O(N),空间复杂度为O(1)。
合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
链接给大家奉上:
https://leetcode.cn/problems/merge-sorted-array/description/
int compar(const void* e1,const void* e2)
{return (*(int*)e1-*(int*)e2);
}
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){int i=0;int j=0;for(i=m;i<m+n;i++){nums1[i]=nums2[j];j++;}qsort(nums1,m+n,sizeof(int),compar);
}
在这里我们先用nums2数组将nums1数组充满,时间复杂度为O(n),qsort函数的时间复杂度为 O(n log n),该代码中n=m+n,所以该代码时间复杂度为 O(n + (m+n) log (m+n))。空间复杂度为O(1)。由于本题所使用解题代码思路十分简单,就不再注释。
本章内容分享到此,感谢各位观看。
相关文章:

时间、空间复杂度的例题详解
文章前言 上篇文章带大家认识了数据结构和算法的含义,以及理解了时间、空间复杂度,那么接下来来深入理解一下时间、空间复杂度。 时间复杂度实例 实例1 // 计算Func2的时间复杂度? void Func2(int N) {int count 0;for (int k 0; k <…...

Ubuntu22.04 搭建 OpenHarmony 命令行开发环境
文章目录 简介安装工具链获取gitee源码安装编译工具编译测试 简介 在本文中,我们将介绍如何使用命令行工具在你的设备上安装OpenHarmony操作系统。OpenHarmony是一个开源的、面向物联网(IoT)设备的操作系统,它提供了一套全面的开…...
)
10.27 知识总结(前端)
一、 前端 1.1 什么是前端? 前端是所有跟用户直接打交道的都可以称之为是前端 比如:PC页面、手机页面、平板页面、汽车显示屏、大屏幕展示出来的都是前端内容 通俗点就是能够用肉眼看到的都是“前端” 1.2 为什么要学前端 学了前端以后我们就可以做全栈工…...

操作系统(02326)考试题库
博客主页:https://tomcat.blog.csdn.net 博主昵称:农民工老王 主要领域:Java、Linux、K8S 期待大家的关注💖点赞👍收藏⭐留言💬 目录 单选题多选题主观题 单选题 把并发进程中与共享变量有关的程序段称为…...
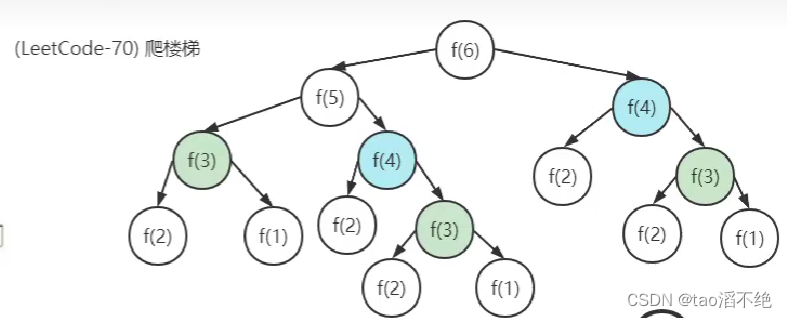
LeetCode题:70爬楼梯,126斐波那契数
目录 70:爬楼梯 题目要求: 解题思路:(类似斐波那契数) 递归解法: 非递归解法: 126:斐波那契数 题目要求: 解题思路: 递归解法: 非递归解…...
VTK OrientationMarker 方向 三维坐标系 相机坐标轴 自定义坐标轴
本文 以 Python 语言开发 我们在做三维软件开发时,经常会用到相机坐标轴,来指示当前空间位置; 坐标轴效果: 相机方向坐标轴 Cube 正方体坐标轴 自定义坐标轴: Code: Axes def main():colors vtkNamedC…...

工控安全与网络安全有什么不同?
在当代,全球制造业正在经历一场前所未有的技术变革。工业4.0不仅代表着自动化和数据交换的进步,它还揭示了工业自动化、智能制造与系统集成的融合。这种集成为企业带来了效率和质量的双重提升,但同时也暴露出新的安全隐患。工控系统成为了这一…...

性能测试工具:Jmeter介绍
JMeter是一个开源的Java应用程序,由Apache软件基金会开发和维护,可用于性能测试、压力测试、接口测试等。 1. 原理 JMeter的基本原理是模拟多用户并发访问应用程序,通过发送HTTP请求或其他协议请求,并测量响应时间、吞吐量、并发…...

Golang Struct 继承的深入讨论和细节
1)结构体可以使用嵌套匿名结构体所有的字段和方法,即:首字母大写或者小写的字段、方法,都可以使用。 type A struct {Name stringage int }func (a *A) SayName() {fmt.Println("A say name", a.Name) }func (a *A) s…...

Android11分区介绍
1.分区汇总 3566及3568分区对应如下: rockdev/Image-rk3566_rgo/ ├── boot.img ├── dtbo.img ├── MiniLoaderAll.bin ├── misc.img ├── parameter.txt ├── recovery.img ├── super.img ├── uboot.img └── vbmeta.img 2.分区说明 分区 说明 boo…...

goland无法调试问题解决
goland 无法调试问题解决 golang 版本升级后,goland 无法进行调试了 首先请看自己下载的版本是否有误 1.apple系 M系列芯片的 arm64版本 2.apple系 intel系列芯片的x86_64 3.windows系 intel解决如下: 查看gopath ericsanchezErics-Mac-mini gww-api…...

关于近期IP-Guard新版本客户端重复发送邮件的问题处理说明
关于近期新版本客户端重复发送邮件的问题处理说明 一、问题描述 近期部分客户反馈,升级到新版本的客户端(4.81.341.0、4.82.621.0及以上),使用SMTP协议发送邮件时,会出现重复发送邮件的情况,主要表现为以下两种现象: Outlook发送包含大量收件人的邮件时,收件人邮箱可能…...

linux java 启动脚本
#!/bin/sh## java env #export JAVA_HOME/data/jdk1.8.0_121 #export JRE_HOME$JAVA_HOME/jre## service name #当前目录 SERVICE_DIR$(cd dirname $0; pwd) echo "$SERVICE_DIR" #jar包路径 JAR_DIRls -ltr $SERVICE_DIR/*.jar| tail -1 echo "JAR_DIR $JAR_DI…...

Node.js 的 CommonJS ECMAScript 标准用法
目录 一、前言二、CommonJS 标准使用方法 三、ECMAScript 标准使用方法 四、常用命令总结 一、前言 本文主要是介绍 Node.js 的 CommonJS & ECMAScript 标准用法 如果对你有帮助,欢迎三连 收藏点赞关注!!! ---- NickYoung 二、…...
Mysql数据库 4.SQL语言 DQL数据查询语言 查询
DQL数据查询语言 从数据表中提取满足特定条件的记录 1.单表查询 2.多表查询 查询基础语法 select 关键字后指定要查询到的记录的哪些列 语法:select 列名(字段名)/某几列/全部列 from 表名 [具体条件]; select colnumName…...
俄罗斯黑客利用Roundcube零日漏洞窃取政府电子邮件
导语:最近,一起涉及Roundcube Webmail的零日漏洞被俄罗斯黑客组织Winter Vivern利用,攻击了欧洲政府机构和智库。这一漏洞已经存在至少一个月,直到10月16日,Roundcube开发团队才发布了安全补丁来修复这个Stored Cross-…...
【Javascript】ajax(阿甲克斯)
目录 什么是ajax? 同步与异步 原理 注意 写一个ajax请求 创建ajax对象 设置请求方式和地址 发送请求 设置响应HTTP请求状态变化的函数 什么是ajax? 是基于javascript的一种用于创建快速动态网页的技术,是一种在无需重新加载整个网页的情况下,…...

Spring MVC的常用注解
目录 RequestMapping 例子: RequestMapping 支持什么类型的请求 使 RequestMapping 只支持特定的类型 RestController 通过 HTTP 请求传递参数给后端 1.传递单个参数 注意使⽤基本类型来接收参数的情况 2.传递多个参数 3.传递对象 4.RequestParam 后端参数…...

vim 使用文档笔记
1. i:进入编辑模式 2. ESC:进入一般命令模式 3. h 或 ←:光标向左移动一个字符 4. j 或 ↓:光标向下移动一个字符 5. k 或 ↑:光标向上移动一个字符 6. l 或 →:光标向右移动一个字符 7. num…...

274. H 指数
文章目录 一、题目1、题目描述2、基础框架3、原题链接 二、解题报告1、思路分析1.1 方案一1.2 方案二 2、时间复杂度3、代码详解3.1 方案一3.2 方案二 三、本题小知识 一、题目 1、题目描述 给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
