“第五十二天”
算术逻辑单元:
之前提过的运算器包括MQ,ACC,ALU,X,PSW;运算器可以实现运算以及一些辅助功能(移位,求补等)。
其中ALU负责运算,运算包括算术运算(加减乘除等)和逻辑运算(与或非,异或等)。ALU能同时处理的比特位数通常等于机器字长。
逻辑运算:
与: Y=A*B ; 类似于乘法,a和b要都为1,输入才能为1;
或: Y=A+B; 类似于加法,a和b有一个为1,输入就为1;
非: Y=Ā;就是取反,a是0,y就是1,a是1,y就是0.
这里还有与或非的门电路,下面的图片。
在逻辑运算中,与 的优先级是大于 或的(与好比乘嘛,乘优先于加)。
逻辑运算也是符合分配律和结合律的,像这样a*(c+d)=ac+ad;(这个就是逻辑表达式)逻辑表达式本质上就是对电路的数学化描述,通过逻辑表达式可以构建出对于的电路,所以简化逻辑表达式实际上也就是在简化电路,还是钱的问题,简化省点钱。
这里在逻辑运算中实际上还有个反演律,可以看一下。
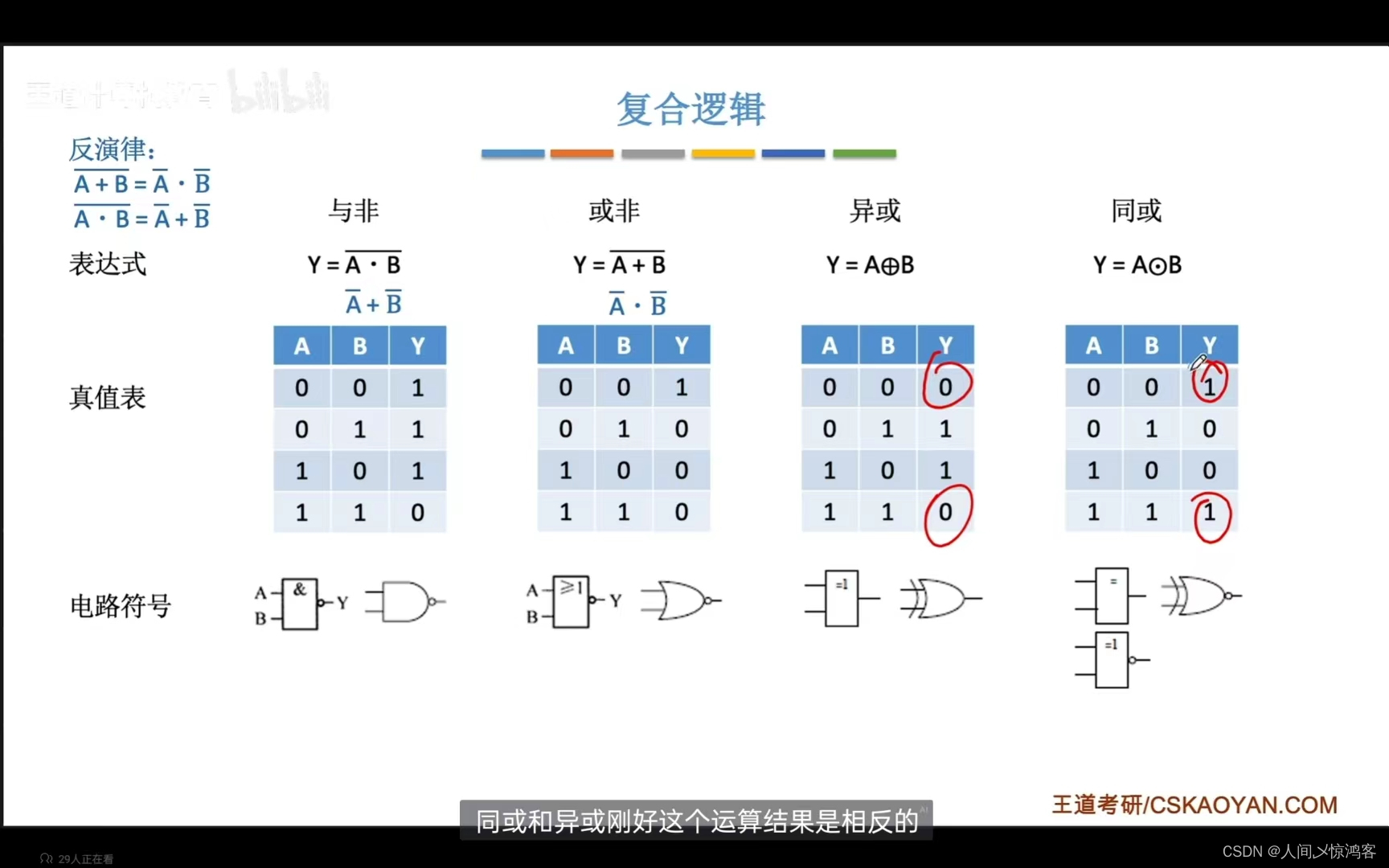 复合逻辑:
复合逻辑:
异或:异或就是相同为 0,不同为1.可以通过异或门电路来求偶校验位。
同或:同或的效果和异或的相反。
还有与非和或非,就是这两个逻辑的结合。
一位全加器:
对于全加器,每次应该有三个输入(当前位的两个数值,来自低位的进位),两个输入(当前位求和的值(本位和),向高位的进位),哎,感觉这都蛮抽象的,用语言不太好描述。
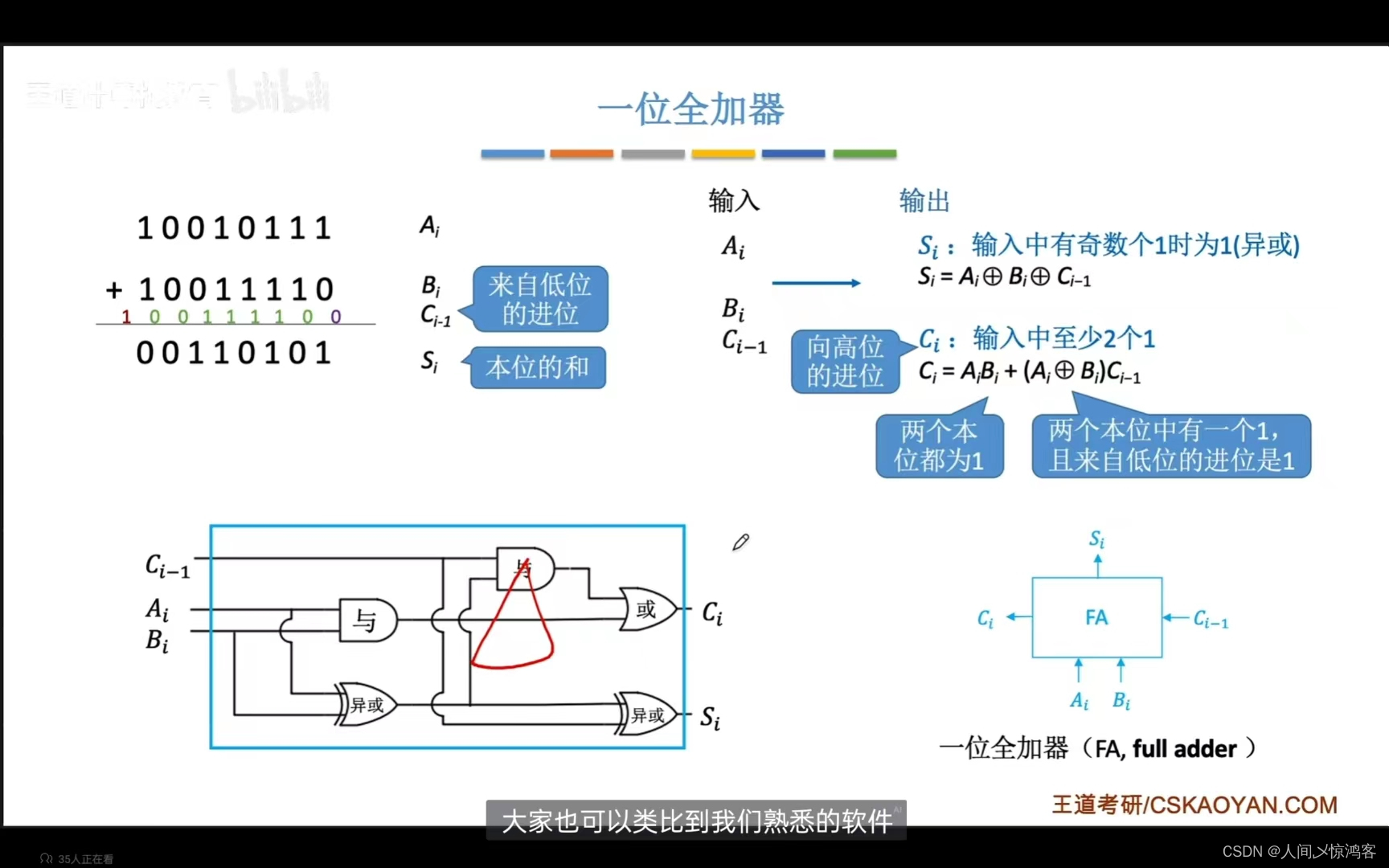
这里对于向高位的进位的实现还是挺有意思的。
然后还有一个串行加法器,其只有一个全加器,但比上面多了个进位触发器(用来保存进位数),数据逐位串行送入加法器中进行运算的时候,进位触发器用来寄存进位信号,以便参与下一次运算。这样的话,如果操作数长n位的话,加法就要分n次进行,每一位产生一位和,并且串行逐位地送回寄存器。
并行加法器:
可以把多个全加器串接起来,每一个全加器处理一位的数据,这样可以进行两个n位数的相加,这样的叫做串行进位的并行加法器.
串行进位又称为行波进位,每一位进位直接依赖于前一位的进位,即进位信号是逐级形成的,这样实际上好像也并不能太多提升运算速度,因为还是要等前面的算完,才能轮到后面的。这里计算速度就主要取决于进位产生的速度,以及数据传递的速度。
并行进位加法器
上面说了依赖低位来获得进位数据的话,会受到进位产生的速度和数据传递速度的影响,这里实际上实际上低位的进位数据,是通过低位运算产生的,那么可以直接通过向处理高位数据的全加器输入高位数据的同时,也输入低位数据,这样就是可以不等待低位的运算结果,而在一开始就进行运算,也就是说第 i 位向更高位的进位可以根据被加数,加数的第 1 ~ i 位,再结合最开始的进位来确定。
根据上面说的可以对并行加法器优化,实现的结果是并行进位的并行加法器,各级进位的信号同时形成,又称为先行进位,同时进位,但这里实际上对于高位来说和最初的那个一位加法器有点一样,从最低位开始算到当前位,可能比一位加法器好在不用反复的读取和输入数据了,一位加法器的每一位的运算结果是要传送到寄存器上的嘛,而这里目的只是当前的高位,过程中求的值无所谓。同时也要指出,随着位的增加,越高位的运算就会越复杂,后面得到结果也会越来越慢。
补码加减运算其:
加法器的原理就是输入被加数和加数(被加数和加数比较长的话,大于机器字长,加法器一次运算是不够的),还有来自低位的进位,通过运算输出 最高位产生的进位和相加的结果,这里实际上还有其他的输出,就是标志位。
补码加/减运算方法:
相加的话,直接按位相加就行;
相减的话,将减数的补码全部按位取反,末位加1(就是正变负,负变正,比如正变负吧,正的原码和补码一样,直接把补码当原码看,这个时候是正数的原码,把符号位取反 0 变 1,这个时候是这个数负数的原码,然后将这个负数的原码变成补码,操作就是符号位不变,其他位按位取反,然后在末位加1嘛,刚刚符号位由正变负的时候已经变过了,所以相当于全部位取反,然后加1.)
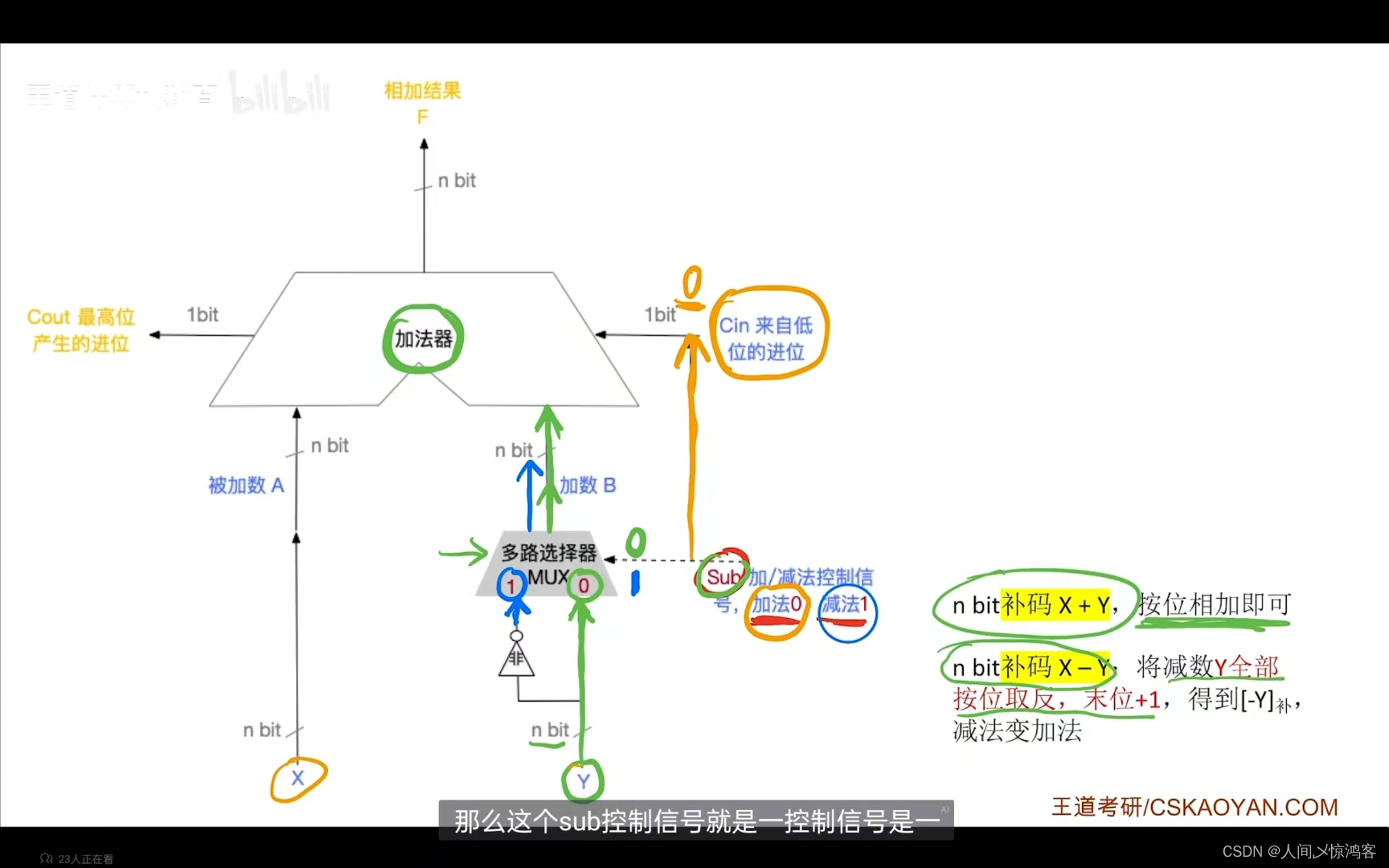
这个不好说,这个就是补码的加法器,它这里多了一个Sub加/减法控制信号,同时向选择器和低位的进位输入信息,如果是加法的话非门是关着的,低位的进位输入是 0 ,这样就都是补码直接参与运算,如果是减法的话,那非门就是打开的,另一边是关着的,这样的话就可以实现减数的全部为按位取反,而末位加一这个操作的实现是通过向低位的进位输入 1 来实现的,这里真的很巧妙,一个输入信号,即控制了加减,又实现了对数据处理,其实两个都是数据的处理,反正就是挺开眼的。
对于无符号整数的加法/减法也可以用该电路实现,其实无符号整数就可以理解为正数,能够处理正数,自然也可以处理无符号整数了。但是无符号整数也会有溢出的出现,注意。
相关文章:

“第五十二天”
算术逻辑单元: 之前提过的运算器包括MQ,ACC,ALU,X,PSW;运算器可以实现运算以及一些辅助功能(移位,求补等)。 其中ALU负责运算,运算包括算术运算(加减乘除等)和逻辑运算(…...
Lvs+Nginx+NDS
什么是?为什么?需要负载均衡 一个网站在创建初期,一般来说都是只有一台服务器对用户提供服务 从图里可以看出,用户经过互联网直接连接了后端服务器,如果这台服务器什么时候突然 GG 了,用户将无法访问这…...

JavaWeb——Servlet原理、生命周期、IDEA中实现一个Servlet(全过程)
6、servlet 6.1、什么是servlet 在JavaWeb中,Servlet是基于Java编写的服务器端组件,用于处理客户端(通常是Web浏览器)发送的HTTP请求并生成相应的HTTP响应。Servlet运行在Web服务器上,与Web容器(如Tomcat&…...

Android 12.0 ota升级之SettingsProvider新增和修改系统数据相关功能实现
1. 前言 在12.0的系统rom定制化开发中,在解决一些已经上线的bug后,进行ota升级的过程中,由于在SettingsProvider中新增了系统属性和修改某项系统属性值,但是在ota升级以后发现没有 更新,需要恢复出厂设置以后才会更改,但是恢复出厂设置 会丢掉一些数据,这是应为系统数据…...
python---for循环结构中的else结构(是同级关系)
为什么需要在for循环中添加else结构 循环可以和else配合使用, else下方缩进的代码指的是当循环正常结束之后要执行的代码。 强调: 循环 正常结束,else之后要执行的代码。 非正常结束,其else中的代码是不会执行的。…...

XLua中lua读写cs对象的原理
LuaCallCS 1. 传递C#对象到Lua XLua在C#维护了两个数据结构,ObjectPool和ReverseMap。 首次传递一个C#对象obj到Lua时,对象被加入到ObjectPool中,并为它创建一个唯一标识objId,建立obj和objId的双向映射。 ObjectPool: objId-…...

新手小白怎么选择配音软件?
现在的配音软件软件很多,各种类型的都比较多,对于新手小白来说不知该如何选择,今天就来给你分享几款好用的配音软件。不论是制作短视频还是制作平常音频都完全可以。 第一款:悦音配音 这是一款专业的视频配音软件,多端…...

linux查看硬件信息命令
文章目录 cpu内核版本内存硬盘主板服务器参考链接 cpu cat /proc/cpuinfo 一个物理CPU可以有1个或者多个物理内核,一个物理内核可以作为1个或者2个逻辑CPU。 物理CPU数就是主板上实际插入的CPU数量。 在Linux上cat /proc/cpuinfo,会打印每个cpu的信息 …...
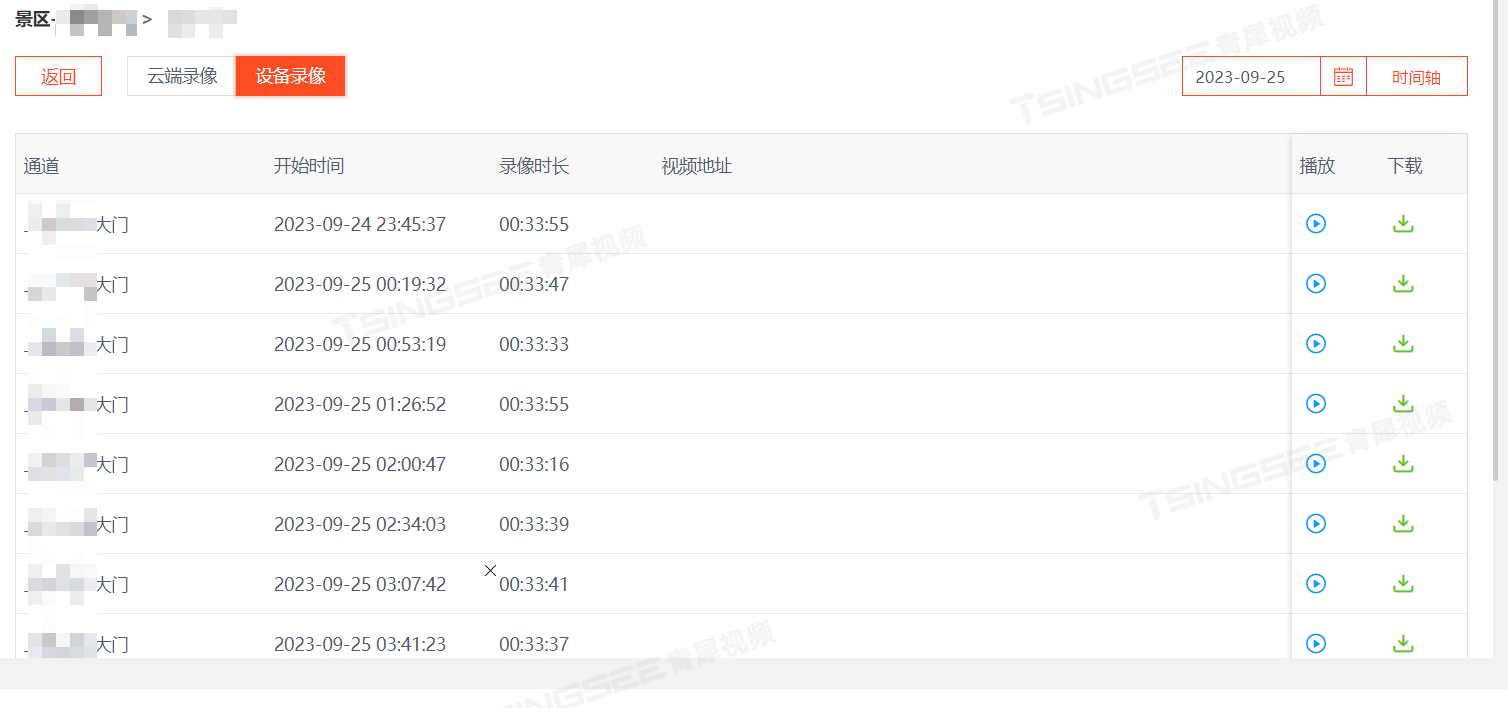
TSINGSEE青犀省级高速公路视频上云联网方案:全面实现联网化、共享化、智能化
一、需求背景 随着高速铁路的建设及铁路管理的精细化,原有的模拟安防视频监控系统已经不能满足视频监控需求,越来越多站点在建设时已开始规划高清安防视频监控系统。高速公路视频监控资源非常丰富,需要对其进行综合管理与利用。通过构建监控…...
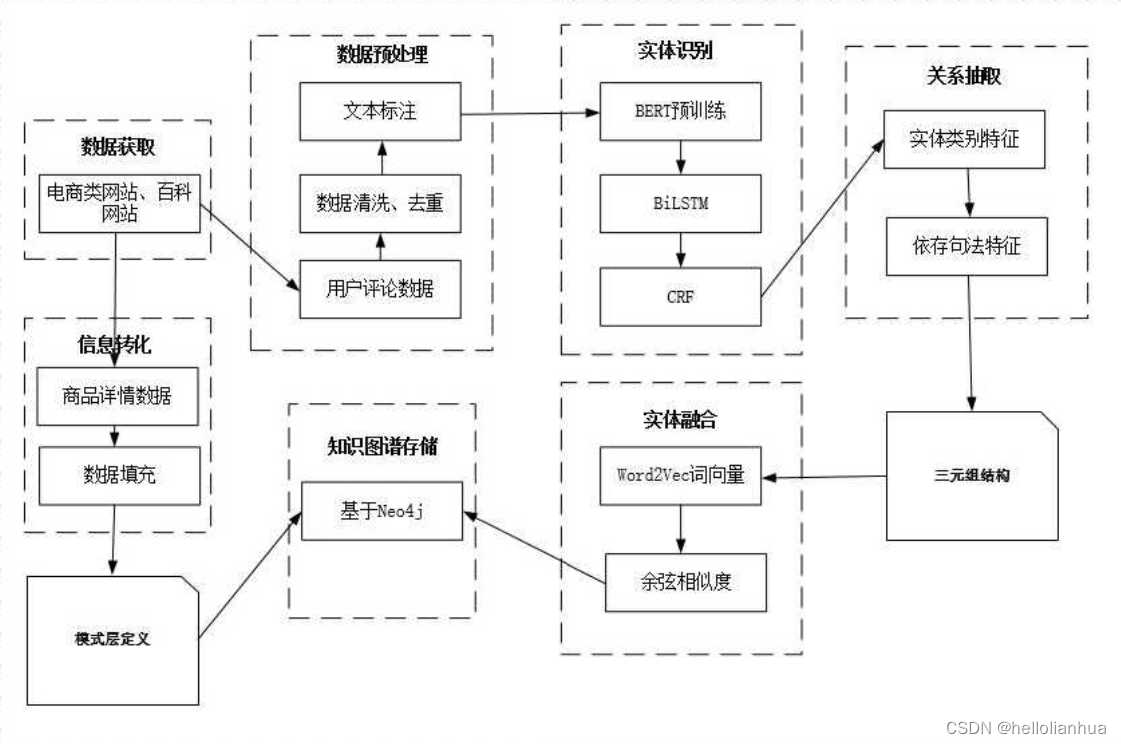
知识图谱相关的操作
微软生成自己的图谱:GitHub - microsoft/SmartKG: This project accepts excel files as input which contains the description of a Knowledge Graph (Vertexes and Edges) and convert it into an in-memory Graph Store. This project implements APIs to searc…...
【Javascript】json
目录 什么是json? 书写格式 json 序列化和反序列化 序列化 反序列化 什么是json? JSON(JavaScript Object Notation)是⼀种轻量级的数据交换格式,它基于JavaScript的⼀个⼦集,易于⼈的编写和阅读,也易于机器解析…...

零资源的大语言模型幻觉预防
零资源的大语言模型幻觉预防 摘要1 引言2 相关工作2.1 幻觉检测和纠正方法2.2 幻觉检测数据集 3 方法论3.1 概念提取3.2 概念猜测3.2.1 概念解释3.2.2 概念推理 3.3 聚合3.3.1 概念频率分数3.3.2 加权聚合 4 实验5 总结 摘要 大语言模型(LLMs)在各个领域…...

智能终端界面自动化测试操作工具 - Appium常见用法
1. Appium 是什么可以做什么? Appium 是一款开源的移动应用自动化测试框架,用于测试移动应用程序的功能和用户界面。它支持多种移动平台,包括 Android 和 iOS,可以使用多种编程语言进行脚本编写,如 Python、Java、Jav…...
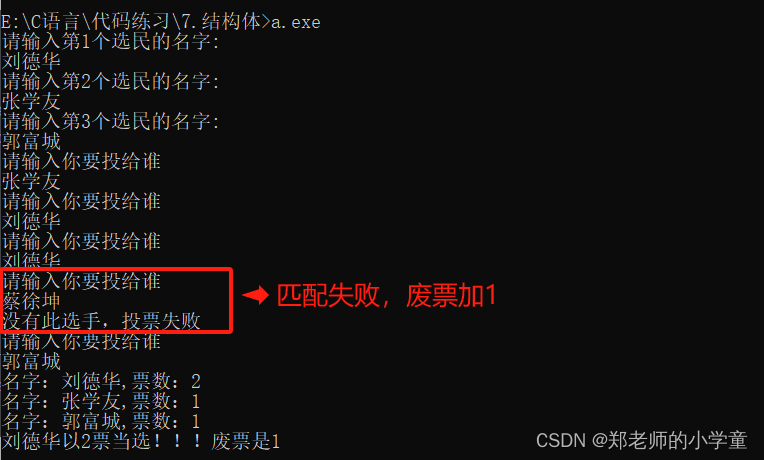
结构体数组经典运用---选票系统
结构体的引入 1、概念:结构体和其他类型基础数据类型一样,例如int类型,char类型,float类型等。整型数,浮点型数,字符串是分散的数据表示,有时候我们需要用很多类型的数据来表示一个整体&#x…...

code too large
描述:比较尴尬,一个方法的代码接近10000行了,部署服务器的时候提示(java :code[255,21] too large),提示代码过长,无法运行。 查看了一下百度:解决的思路 JVM规范:「类或接口可以声明的字段数量限制在 655…...

vue中把弹出层.vue文件注册成组件供其他.vue文件调用的写法
背景:因弹出层多个页面的详情都是一样的,因此把弹出层定义成组件,多次调用 定义组件的过程中出现很多问题,因此再次记录最终成功的写法 一、 简单实现页面调用弹出层组件的打开弹出层方法: 1. 弹出层组件 (in…...
mac 查看GPU使用
首先搜索活动监视器 然后 点击窗口->gpu历史记录 记住不是立马出结果,而是 需要等半分钟左右的...
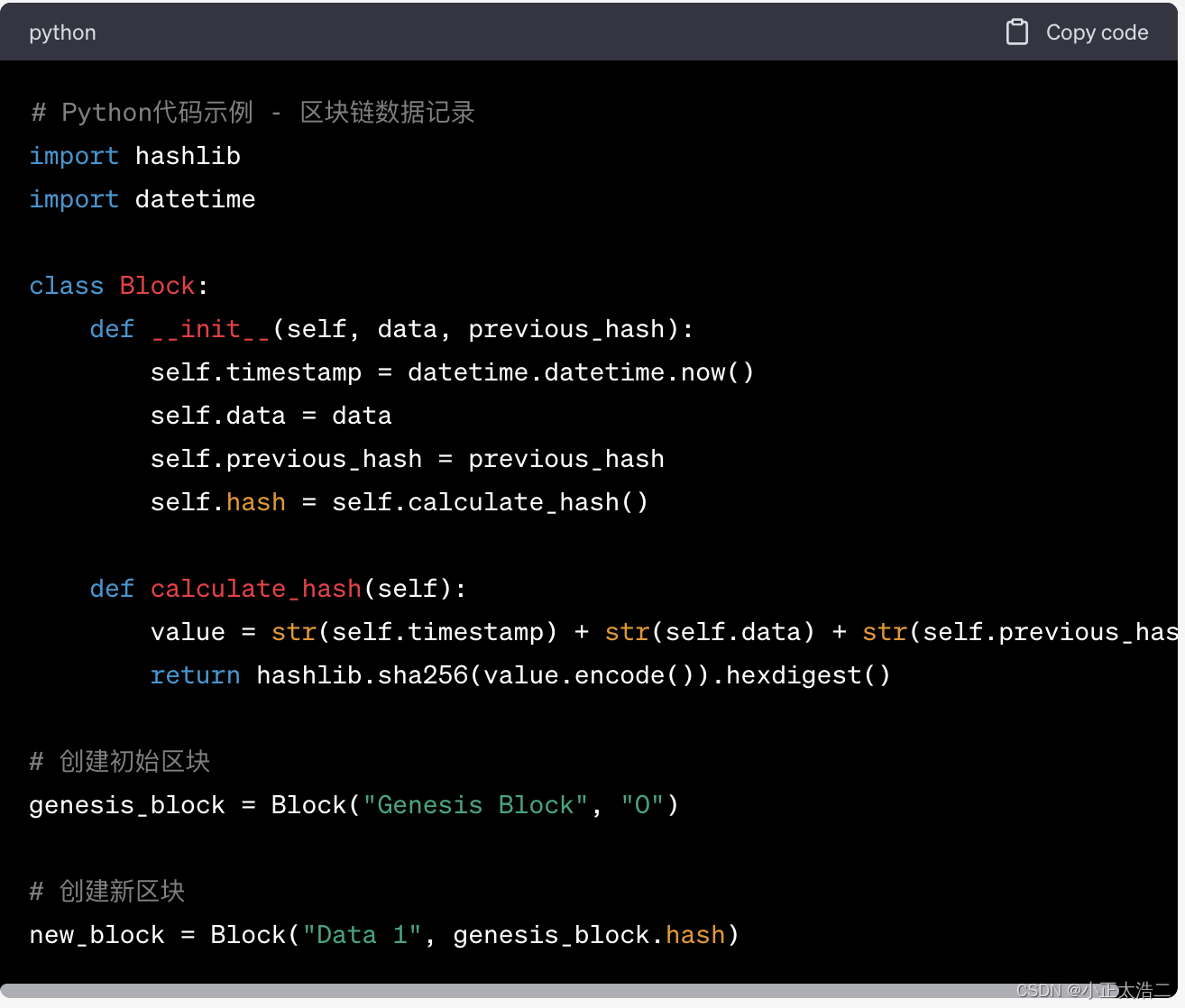
工业4.0的安全挑战与解决方案
在当今数字化时代,工业4.0已经成为制造业的核心趋势。工业4.0的兴起为生产企业带来了前所未有的效率和灵活性,但与之伴随而来的是一系列的安全挑战。本文将深入探讨工业4.0的安全挑战,并提供一些解决方案,以确保制造业的数字化转型…...
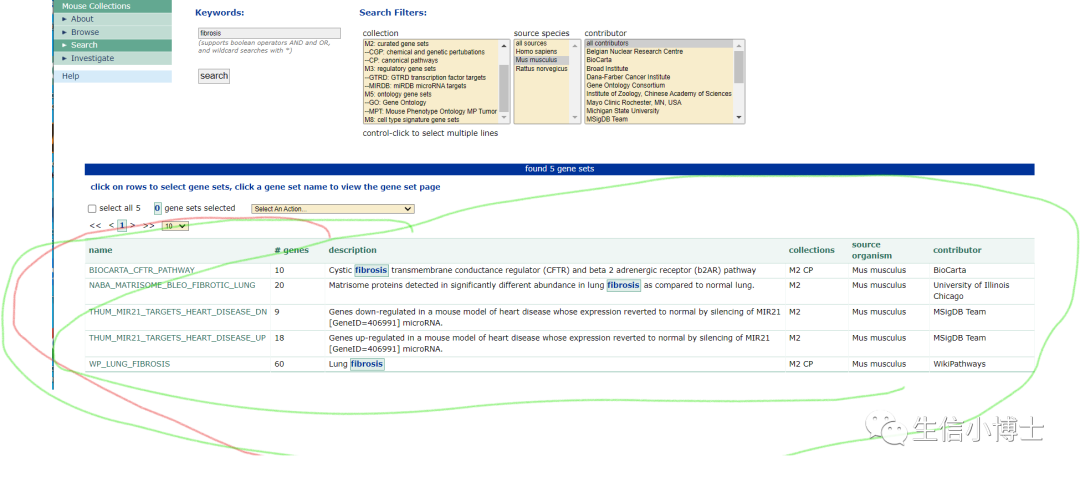
如何查找特定基因集合免疫基因集 炎症基因集
温故而知新,再次看下Msigdb数据库。它更新了很多内容。给我们提供了一个查询基因集的地方。 关注微信:生信小博士 比如纤维化基因集: 打开网址:https://www.gsea-msigdb.org/gsea/msigdb/index.jsp 2.点击search 3.比如我对纤维…...

轮转数组(Java)
大家好我是苏麟 , 这篇文章是凑数的 ... 轮转数组 描述 : 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 题目 : 牛客 NC110 旋转数组: 这里牛客给出了数组长度我们直接用就可以了 . LeetCode 189.轮转数组 : 189. 轮…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
