Python数据结构——树
树(Tree)是一种重要的数据结构,它在计算机科学中被广泛应用,用于构建层次结构、组织数据和解决各种问题。本文将详细介绍Python中树数据结构的使用,包括二叉树、二叉搜索树、平衡二叉树等,并提供示例代码来说明它们的用途。
二叉树(Binary Tree)
二叉树是一种树数据结构,其中每个节点最多有两个子节点:左子节点和右子节点。以下是如何使用Python创建和操作二叉树的示例:
- 创建二叉树节点
class TreeNode:def __init__(self, value):self.value = valueself.left = Noneself.right = None
- 构建二叉树
# 创建根节点
root = TreeNode(1)# 添加子节点
root.left = TreeNode(2)
root.right = TreeNode(3)# 添加更多子节点
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
- 遍历二叉树
二叉树的遍历方式包括前序遍历、中序遍历和后序遍历。以下是中序遍历的示例:
def inorder_traversal(node):if node:inorder_traversal(node.left)print(node.value)inorder_traversal(node.right)inorder_traversal(root)
二叉搜索树(Binary Search Tree)
二叉搜索树(BST)是一种特殊的二叉树,其中左子树的值都小于根节点的值,右子树的值都大于根节点的值。BST具有快速查找、插入和删除元素的特性。以下是如何使用Python创建和操作BST的示例:
- 创建BST节点
class TreeNode:def __init__(self, value):self.value = valueself.left = Noneself.right = None
- 插入元素
def insert(root, value):if not root:return TreeNode(value)if value < root.value:root.left = insert(root.left, value)else:root.right = insert(root.right, value)return root
- 查找元素
def search(root, value):if not root or root.value == value:return rootif value < root.value:return search(root.left, value)return search(root.right, value)
- 删除元素
def delete(root, value):if not root:return rootif value < root.value:root.left = delete(root.left, value)elif value > root.value:root.right = delete(root.right, value)else:if not root.left:return root.rightelif not root.right:return root.leftroot.value = find_min(root.right)root.right = delete(root.right, root.value)return rootdef find_min(node):current = nodewhile current.left:current = current.leftreturn current.value
平衡二叉树(Balanced Binary Tree)
平衡二叉树是一种特殊的BST,它确保树的高度差不会过大,以保持高效的查找、插入和删除操作。常见的平衡二叉树包括AVL树和红黑树。以下是如何使用Python的第三方库sortedcontainers创建和操作AVL树的示例:
- 安装sortedcontainers库
pip install sortedcontainers
- 创建AVL树
from sortedcontainers import SortedDictavl_tree = SortedDict()
- 插入元素
avl_tree[1] = 'One'
avl_tree[2] = 'Two'
avl_tree[3] = 'Three'
- 查找元素
print(avl_tree[2]) # 输出: 'Two'
应用场景
树数据结构在计算机科学中有着广泛的应用,包括但不限于:
-
数据结构:树用于构建数据结构,如图、堆、栈、队列等。
-
数据索引:树用于数据库索引、搜索引擎索引和文件系统索引。
-
表达式求值:树用于构建语法树,用于解析和求值表达式。
-
算法设计:树用于许多算法,如排序、搜索、图算法等。
-
文件系统:文件系统通常使用树结构来组织文件和目录。
-
数据压缩:哈夫曼树用于数据压缩。
总结
树是一种重要的数据结构,用于组织和管理数据,具有广泛的应用。在Python中,你可以使用自定义类来实现二叉树、二叉搜索树,也可以使用第三方库来创建平衡二叉树。了解树数据结构及其应用场景将有助于你更好地解决各种编程问题,从算法设计到数据库管理,都需要树来组织和管理数据。无论是在数据结构设计、算法实现、数据库管理还是编程竞赛中,树都是一个非常有用的工具。
相关文章:

Python数据结构——树
树(Tree)是一种重要的数据结构,它在计算机科学中被广泛应用,用于构建层次结构、组织数据和解决各种问题。本文将详细介绍Python中树数据结构的使用,包括二叉树、二叉搜索树、平衡二叉树等,并提供示例代码来…...
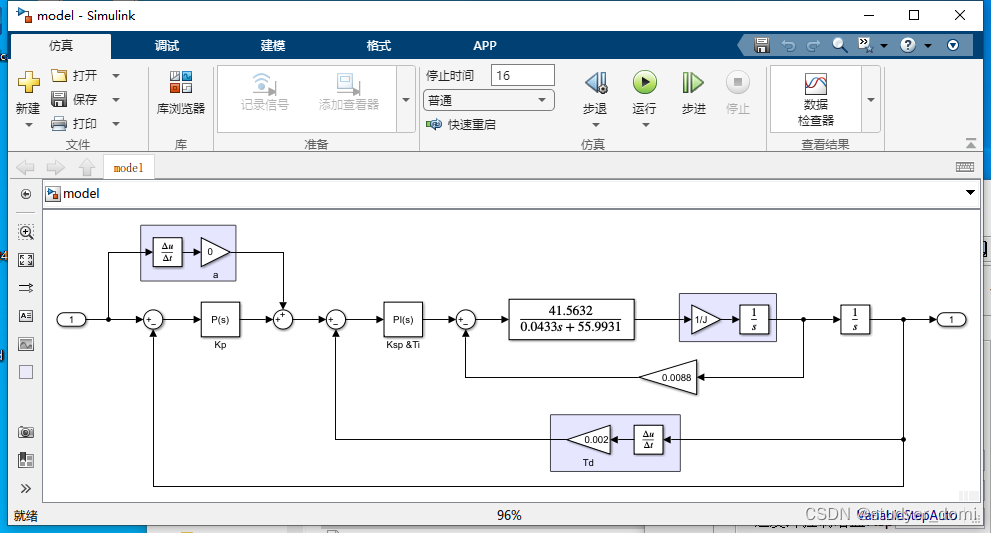
Simulink和GUI联合使用
1、内容简介 略 9-可以交流、咨询、答疑 2、内容说明 Simulink和GUI联合使用 Simulink、GUI、参数传递 3、仿真分析 4、参考论文 略...
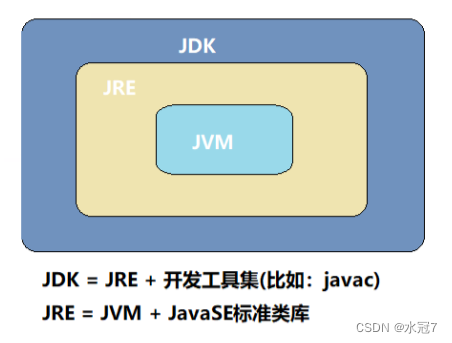
【0基础学Java第一课】-- 初始Java
目录 1. 初识java1.1 Java是什么1.2 Java应用领域1.3 Java语言发展简史1.4 Java语言特性1.5 JRE与JDK1.6 Java开发环境1.6.1 安装JDK1.6.2 配置环境变量 1.7 初始Java中main函数1.7.1 JDK、JRE、JVM之间的关系 1.8 注释1.9 标识符1.10 关键字 1. 初识java 1.1 Java是什么 Jav…...

osg3.4的插件及功能
OpenSceneGraph(OSG) 学习之 核心结构(基础篇)-CSDN博客 OSG源码中主要包含17个库,每个库的功能如所示表 1 OSG核心库功能...

『力扣刷题本』:轮转数组
一、题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3 步: [5,6,…...
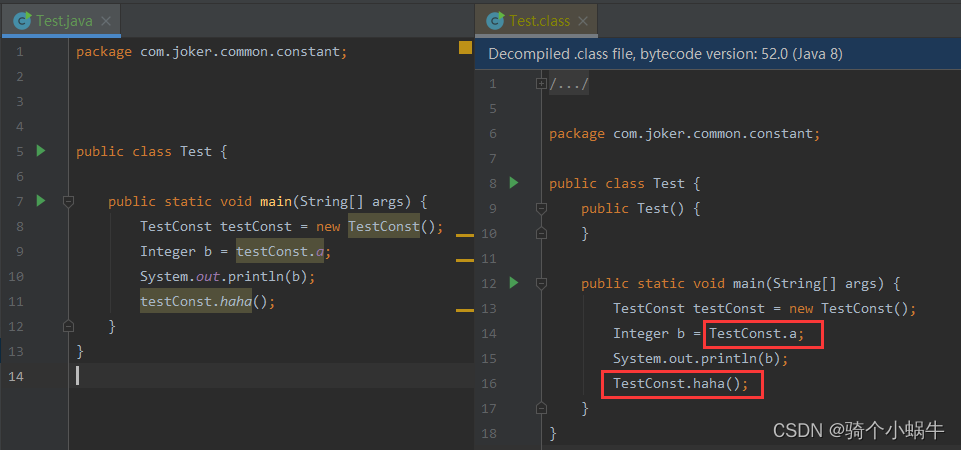
Java关于实例对象调用静态变量和静态方法问题
直接去看原文 原文链接:Java关于实例对象调用静态变量和静态方法问题_java对象可以调用static方法吗_骑个小蜗牛的博客-CSDN博客 --------------------------------------------------------------------------------------------------------------------------------- 实例…...

【开源】基于SpringBoot的海南旅游景点推荐系统的设计和实现
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 用户端2.2 管理员端 三、系统展示四、核心代码4.1 随机景点推荐4.2 景点评价4.3 协同推荐算法4.4 网站登录4.5 查询景点美食 五、免责说明 一、摘要 1.1 项目介绍 基于VueSpringBootMySQL的海南旅游推荐系统ÿ…...

字符串中的assert和strcat
assert:函数原型是:void assert( int expression );其作用是现计算表达式 expression ,如果其值为假(即为0),那么它先 stderr 打印一条出信息,然后通过调用 abort 来终止程序运行。使用assert 的缺点是,频繁的调用会影…...
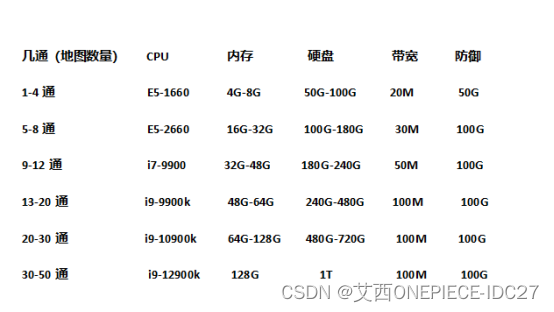
方舟生存进化ARK个人服务器搭建教程保姆级
方舟生存进化ARK个人服务器搭建教程保姆级 大家好我是艾西,在很久之前我有给大家分享过方舟生存进化的搭建架设教程,但时间久远且以前的教程我现在回头看去在某些地方说的并不是那么清楚。最近也是闲暇无事打算重新巩固下方舟生存进化的搭建架设教程&…...

SpringBoot可以连接RabbitMQ集群吗 ?
目录 一、SpringBoot可以连接RabbitMQ集群吗?二、springboot连接到rabbitmq集群可以负载均衡吗?三、SpringBoot既然可以配置负载均衡,为什么还需要Haproxy做负载均衡? 一、SpringBoot可以连接RabbitMQ集群吗? Spring …...

【机器学习】KNN算法-模型选择与调优
KNN算法-模型选择与调优 文章目录 KNN算法-模型选择与调优1. 交叉验证2. 超参数搜索-网格搜索(Grid Search)3. 模型选择与调优API4. 鸢尾花种类预测-代码和输出结果5. 计算距离 问题背景:KNN算法的K值不好确定 1. 交叉验证 交叉验证&#x…...

NPM【问题 01】npm i node-sass@4.14.1报错not found: python2及Cannot download问题处理
node-sass安装问题处理 1.问题2.处理2.1 方案一【我的环境失败】2.2 方案二【成功】2.3 方案三【成功】 1.问题 gyp verb which failed Error: not found: python2 # 1.添加Python27的安装路径到环境变量 gyp verb check python checking for Python executable "python…...

redis集群中节点fail,noaddr
文章目录 1. 问题:fail,noaddr2. cluster nodes节点信息解读2.1 每个字段的含义2.2 flags字段各标记含义 3. redis集群fail,noaddr问题解决4. cluster指令5. 相关文章(1) redis集群搭建(2) 华为云两台机器内网互联(3) /etc/rc.d/init.d 详解|程序开机自启(4) Redis5…...
Fourier分析导论——第1章——Fourier分析的起源(E.M. Stein R. Shakarchi)
第 1 章 Fourier分析的起源 (The Genesis of Fourier Analysis) Regarding the researches of dAlembert and Euler could one not add that if they knew this expansion, they made but a very imperfect use of it. They were both persuaded that an arbitrary and d…...
使用Node.js软件包管理器(npm)安装TypeScript
安装node.js node.js的安装很简单,这里不再赘述,如果大家有需要,可以看一下这个:https://blog.csdn.net/David_house/article/details/123218488 检验电脑上node.js是否安装成功,或者是否已经安装node.js,…...
鸿蒙ArkUI-X跨端应用开发,一套代码构建多平台应用
文章目录 一、项目介绍二、技术架构三、Gitee仓库地址四、ArkUI-X开发者文档五、快速开始——环境准备1、下载DevEco Studio,版本V4.0 Beta2以上2、打开DevEco,下载相关环境配置3、配置开发环境3.1、OpenHarmony SDK3.2、安装ArkUI-X SDK3.2、Android SD…...

【鸿蒙软件开发】ArkTS基础组件之Gauge(环形图表)、LoadingProgress(动态加载)
文章目录 前言一、Gauge环形图表1.1 子组件1.2 接口参数介绍 1.2 属性1.3 示例代码二、LoadingProgress2.1 子组件2.2 接口2.3 属性2.4 示例代码 总结 前言 Gauge:数据量规图表组件,用于将数据展示为环形图表。 LoadingProgress:用于显示加载…...
C++模板类用作参数传递
前言 在模板类<>传递参数的一种实现。记不住,以此记录。 // dome.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。 // #define _CRT_SECURE_NO_WARNINGS #include <iostream> //#include "tools.h" #include <fu…...
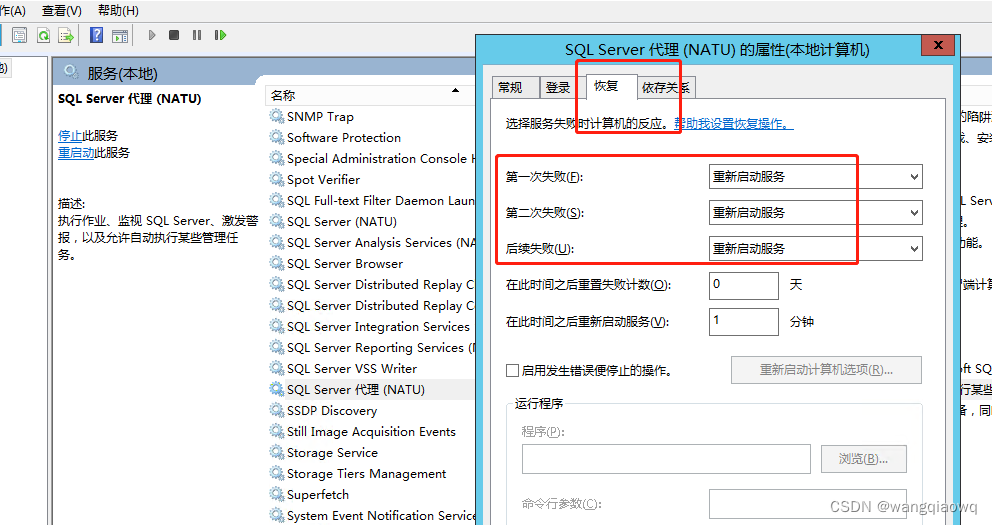
SQL server 代理服务启动和查看
设置重启 使用管理员权限登录到运行 SQL Server 代理服务的计算机。 打开 Windows 服务管理器。可以通过按下 Windows 键 R,然后键入 "services.msc" 并按 Enter 来打开服务管理器。 在服务列表中,找到 "SQL Server Agent" 服务&…...

单例模式详解【2023年最新】
一、单例模式概念 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点来访问该实例。它的目的是限制一个类只能创建一个对象,以确保在整个应用程序中只有一个共享的实例。 单例模式通常用于以下情况:…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
