centos jdk 安装
1、oracle官网下载jdk8
https://www.oracle.com/java/technologies/javase/javase-jdk8-downloads.html
2、楼主用的以前下载好的安装包jdk-8u111-linux-x64.gz。下载后使用工具如Xftp将安装包上传到/opt目录下,这里随便什么目录都行,并解压安装包。
cd /opt #cd到上传目录
tar -zxvf jdk-8u111-linux-x64.gz #解压压缩包
1
2
3、解压完成后,当前目录会有一个jdk1.8.0_111的文件夹。将文件夹移动到/usr/local/java下(一般安装的软件都会放到/usr/local/目录下)。
mv jdk1.8.0_111/ /usr/local/java #将文件移动到usr/local/目录下,并将文件夹名改为java
1
4、设置环境变量
vim /etc/profile #编辑profile文件
1
在文件末尾加上如下代码,保存退出。
export JAVA_HOME=/usr/local/java
export CLASSPATH=.:$JAVA_HOME/lib/dt.jar:$JAVA_HOME/lib/tools.jar:$JAVA_HOME/jre/lib/rt.jar
export PATH=$PATH:$JAVA_HOME/bin
5、使环境变量生效
source /etc/profile
6、验证是否安装完成
java -version
javac -version
相关文章:

centos jdk 安装
1、oracle官网下载jdk8 https://www.oracle.com/java/technologies/javase/javase-jdk8-downloads.html 2、楼主用的以前下载好的安装包jdk-8u111-linux-x64.gz。下载后使用工具如Xftp将安装包上传到/opt目录下,这里随便什么目录都行,并解压安装包。 c…...
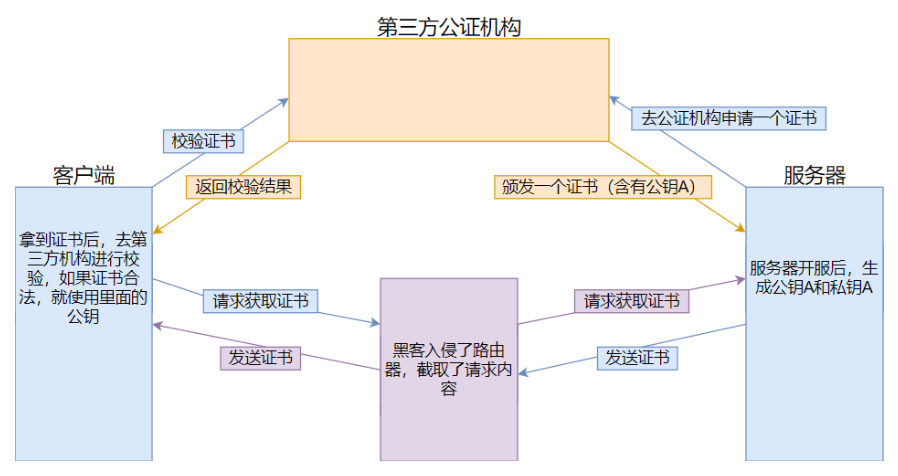
【计算机网络】什么是HTTPS?HTTPS为什么是安全的?
【面试经典题】 前言: HTTP最初的设计就是用于数据的共享和传输,并没有考虑到数据的安全性,如窃听风险,篡改风险和冒充风险。HTTPS是在 HTTP 的基础上引入了一个加密层。HTTPS通过数据加密,数据完整性检验和身份认证…...
Windows-Oracle19c 安装详解-含Navicate远程连接配置 - 同时连接Oracle11g和Oracle19c
文章目录 0 说明1 下载链接2 安装:一定要以管理员身份运行,不然后面有可能会报错。3 启动监听4. 登录Oracle4 Navicate远程连接-配置监听4.1 修改监听文件4.2 网络配置助手-配置本地监听端口4.3 Navicate连接成功 5 Navicate同时连接两个Oracle数据库 0 …...

文件权限详解
一、文件类型 ll指令查看文件详细信息中,第一列就是文件类型。 常见的文件类型有: 1、 - :普通文件 (文本、源代码、图片、视频、可执行) 2、 d :目录文件 3、b :块设备 4、c ࿱…...

在声明和定义的一些小坑
1、静态成员变量的初始化 静态成员变量声明在 .h 头文件文件中,初始化应该在 .cpp 源文件中 就会出现"找到一个或多个多重定义的符号",下面的错误 class MyString{public:typedef char* iterator;typedef const char* const_iterator;iterator begin();…...
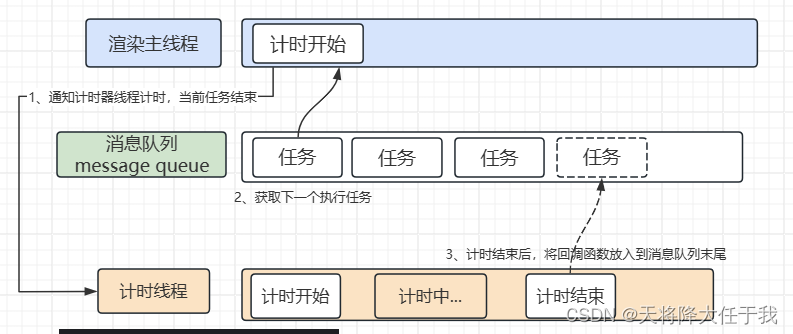
浏览器事件循环 (event loop)
进程与线程 进程 进程的概念 进程是操作系统中的一个程序或者一个程序的一次执行过程,是一个动态的概念,是程序在执行过程中分配和管理资源的基本单位,是操作系统结构的基础。 简单的来说,就是一个程序运行开辟的一块内存空间&a…...
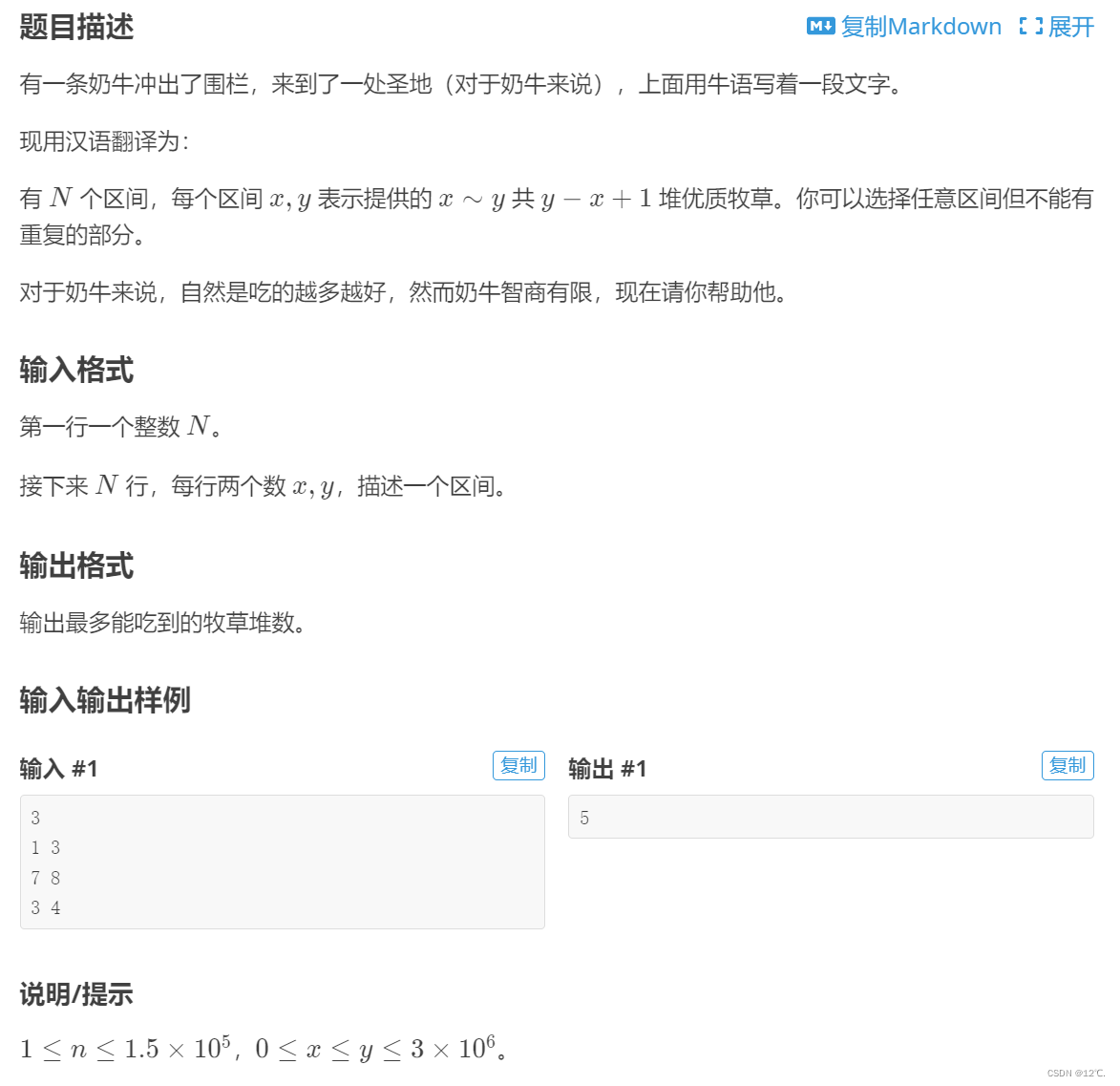
P1868 饥饿的奶牛
根据题意可以知道是一个动态规划,看完数据范围之后可以知道是一个线性DP。 解决方法有点类似于背包问题,枚举背包的每一个空间。 如果把坐标轴上每个点都看成一个块儿,只需要按顺序求出前 i 个块儿的最大牧草堆数,f[i] 就是前i的…...
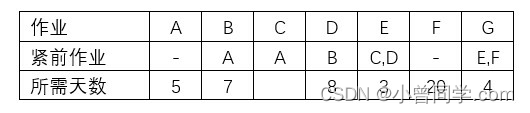
【软考系统架构设计师】2021年系统架构师综合知识真题及解析
本文主要分享2021年下半年系统架构师综合知识历年真题以及本人在做题时的所思所想。题目序号有点混乱,可忽略 【01】.某计算机系统页面大小为4K,进程P1的页面变换表如下图所示,看P1要访问数据的逻辑地址为十六进制1B1AH,那么该逻辑地址经过变…...
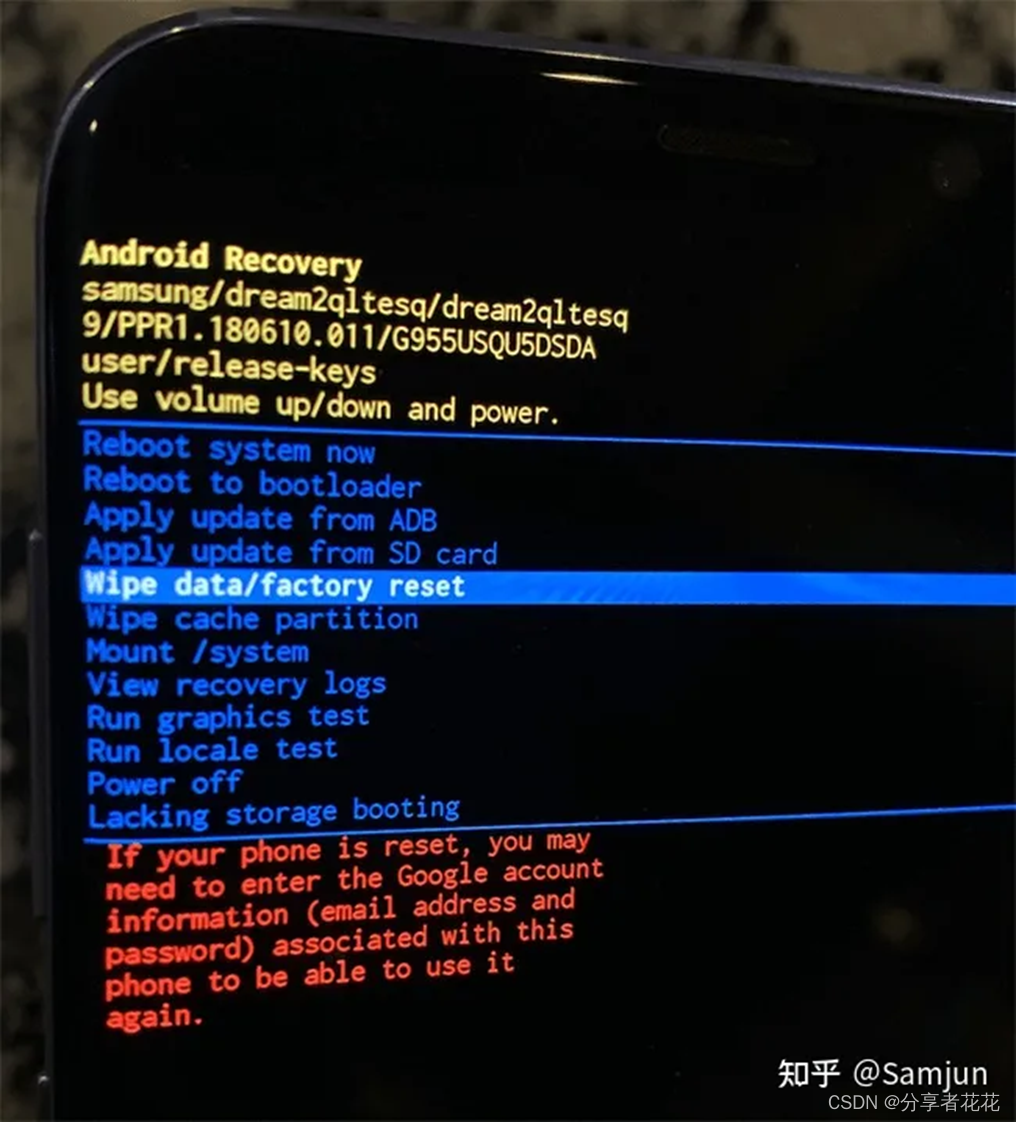
如何在忘记手机密码或图案时重置 Android 手机?
忘记手机密码或图案是 Android 用户一生中不得不面对的最令人沮丧的事情之一。恢复 Android 设备的唯一方法是在 Android 设备上恢复出厂设置。但许多用户不使用此方法,因为此过程会擦除您设备上可用的所有个人数据。 但是,有一种方法可以在不丢失任何数…...

LeetCode每日一题——2520. Count the Digits That Divide a Number
文章目录 一、题目二、题解 一、题目 2520. Count the Digits That Divide a Number Given an integer num, return the number of digits in num that divide num. An integer val divides nums if nums % val 0. Example 1: Input: num 7 Output: 1 Explanation: 7 di…...

论文阅读——DistilBERT
ArXiv:https://arxiv.org/abs/1910.01108 Train Loss: DistilBERT: DistilBERT具有与BERT相同的一般结构,层数减少2倍,移除token类型嵌入和pooler。从老师那里取一层来初始化学生。 The token-type embeddings and the pooler a…...

202212 青少年等级考试机器人实操真题三级
202212 青少年等级考试机器人实操真题三级 考试时间:60分钟 总分:100 及格分:60 一、问答题 (共1题,每题100分) 1、实际操作(共1题,共100分) 请考生在实操考试结束前将本题作答程序文件按“说明”要求完成上传。 1. 主…...
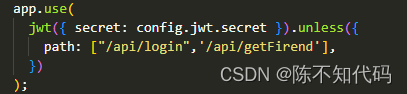
token正确不报错,token失效后却出现报跨域错误
1.今天在使用koajs开发项目时,突然发现前端配置axios的response获取不到后端定义的token失效内容了,取而代之的是出现了跨域的错误。 2. 我马上去查找koajs的跨域中间件配置,发现配置完好cors,token正确时,接口正常访问…...

STM32中除零运算,为何程序不崩溃?
在 C 语言中,除零运算会导致异常吗? 在 C 语言中,当一个数除以零时,会导致除法运算错误,通常表现为“除以零”错误或被称为“浮点异常”(floating-point exception)。 对于整数除法,…...

sprinbboot 2.7启动不生成日志文件
新增了一个springboot项目,通过idea 调试,并且在idea 的vm options中指定-Dlogging.configclasspath:logback-pro.xml 或者 -Dlogging.configclasspath:logback-dev.xml 都能正常生成对应的日志文件。 部署到测试环境以及生产环境,日志文件却…...

Kafka - 3.x 图解Broker总体工作流程
文章目录 Zk中存储的kafka的信息Kafka Broker总体工作流程1. broker启动后向zk中注册2. Controller谁先启动注册,谁说了算3. 由选举出来的Controller监听brokers节点的变化4. Controller决定leader选举5. Controller将节点信息上传到Zk中6. 其他Controller从zk中同步…...

APP自动化测试 ---- Appium介绍及运行原理
在面试APP自动化时,有的面试官可能会问Appium的运行原理,以下介绍Appium运行原理。 一、Appium介绍 1.Appium概念 Appium是一个开源测试自动化框架,可用于原生,混合和移动Web应用程序测试。它使用WebDriver协议驱动IOS…...

学习模板发布
学习目标: 提示:这里可以添加学习目标 例如: 一周掌握 Java 入门知识 学习内容: 提示:这里可以添加要学的内容 例如: 搭建 Java 开发环境掌握 Java 基本语法掌握条件语句掌握循环语句 学习时间&#x…...

Hive 视图和索引
1.视图 1.1 简介 Hive 中的视图和 RDBMS 中视图的概念一致,都是一组数据的逻辑表示,本质上就是一条 SELECT 语句的结果集。视图是纯粹的逻辑对象,没有关联的存储 (Hive 3.0.0 引入的物化视图除外),当查询引用视图时,Hive 可以将视图的定义与查询结合起来,例如将查询中的过…...
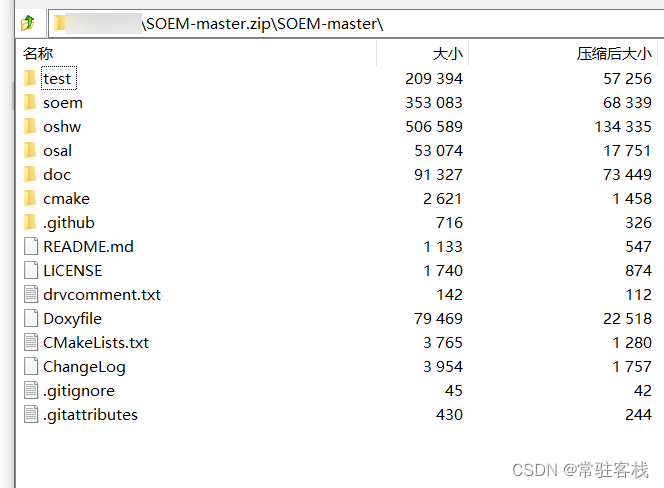
EtherCAT主站SOEM-- 0 SOEM下载编译及文件功能介绍
0 介绍EtherCAT主站SOEM文件及主要功能函数 1. soem介绍:2 soem主要功能文件说明:3 soem下载链接4 编译soem4.1 Windows (Visual Studio):4.2 Linux & macOS: 该文档修改记录:总结 1. soem介绍: SOEM&…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...
