人生岁月年华
人生很长吗?不知道。只知道高中坐在教室里,闹哄哄的很难受。也记得上班时无聊敲着代码也很难受。
可是人生也不长。你没有太多时间去试错,你没有无限的时间精力去追寻你认为的高大上。
人生是何体验呢?人生的感觉很多吧。大多数人生的主题就是上学,工作。上学无非就是开心不开心,努力不努力,意义不意义,自己喜欢的女生喜不喜欢自己,偷偷地去翻墙上网。工作也就是像一只被领导抽打的陀螺,不停地旋转。而自己作为一直取悦他人的陀螺,则转的越来越好,越来越稳。
人生靠自己吗?不靠自己,把自己的思考,自己的困境,自己的事情,自己虽然难于解决,推给他人,倒也不是件仁义的事情。
只记得人生这么多年。与这么多人相处的愉快与不愉快。作为一个敏感者,作为一个弱者,作为一个内向者,一段不好的关系中总是处于下风,总是内耗也是一件悲惨的事情。
人生是什么呢?是虽然遭受着生活的痛苦,但是总有天晴的时候。天晴的时候,心情也很好。人生很长,意义和希望不就是在未来吗?
不想去回忆太多的美好。因为一是记不住,二是逝去的美好让人纠结。别人是什么样的人,别人做什么样的事,对我来说,也不过是个谜一样的事情。我大概就是活在当下和未来的人。我记不得过去,因为现在和未来有更值得焦虑的事情等我去积累记忆和能量去解决。我总是焦虑着未来一年,两年发生的事情。比如上学毕业时纠结于工作的未来,婚后的幸福度。现在呢,则也是如此。只不过预期不一致罢了。
当下的幸福不是也很重要吗?虽然记得起过去的美好对我是一件奢望。买一杯奶茶,开车去旅旅游,逛逛街也是蛮好的事情。富养自己,不就是把当下的自己弄的开开心心,幸幸福福的样子吗?
人性,人性不过是和别人交往时,别人会做些什么。比如说:你感觉别人看到你的缺点时,会暗暗笑你吗?职场上,别人会暗戳戳的找你的茬吗?你会对爱情坚守吗?谈人性大多数谈的就是职场人,朋友,家人什么时间什么场合什么事情会对你好,不理你,对你坏。
时间就在这里,我就这么静静地坐着,无力改变,没有精力去改变。唯有写篇文章,让自己心静,才是最现实的幸福。
相关文章:

人生岁月年华
人生很长吗?不知道。只知道高中坐在教室里,闹哄哄的很难受。也记得上班时无聊敲着代码也很难受。 可是人生也不长。你没有太多时间去试错,你没有无限的时间精力去追寻你认为的高大上。 人生是何体验呢?人生的感觉很多吧。大多数…...
电脑QQ如何录制视频文件?
听说QQ可以录制视频,还很方便,请问该如何录制呢?是需要先打开QQ才可以录制吗?还是可以直接使用快捷键进行录制呢?录制的质量又如何呢? 不要着急,既然都打开这篇文章看了,那小编今天…...

python:多波段遥感影像分离成单波段影像
作者:CSDN @ _养乐多_ 在遥感图像处理中,我们经常需要将多波段遥感影像拆分成多个单波段图像,以便进行各种分析和后续处理。本篇博客将介绍一个用Python编写的程序,该程序可以读取多波段遥感影像,将其拆分为单波段图像,并保存为单独的文件。本程序使用GDAL库来处理遥感影…...

天堂2游戏出错如何解决
运行游戏时出现以下提示:“the game may not be consistant because AGP is deactivated please activate AGP for consistancy” 这个问题的原因可能是由于您的显示卡的驱动或者主板的显示芯片组的驱动不是新开。或您虽然已经更新了您的显示卡的驱动程序࿰…...
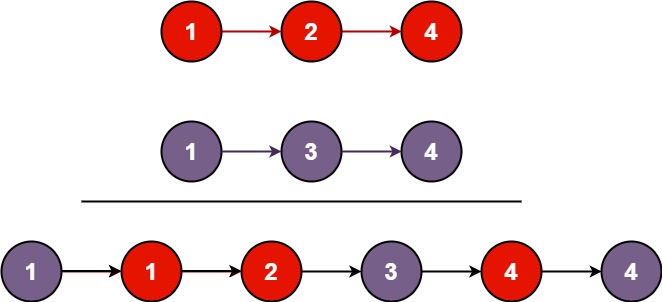
『力扣刷题本』:合并两个有序链表(递归解法)
一、题目 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1: 输入:l1 [1,2,4], l2 [1,3,4] 输出:[1,1,2,3,4,4]示例 2: 输入:l1 [], l2 [] 输出&#x…...
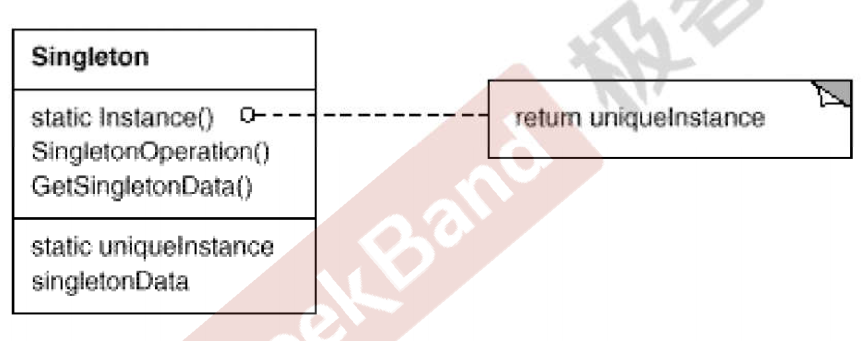
C++设计模式_12_Singleton 单件模式
在之前的博文C57个入门知识点_44:单例的实现与理解中,已经详细介绍了单例模式,并且根据其中内容,单例模式已经可以在日常编码中被使用,本文将会再做梳理。 Singleton 单件模式可以说是最简单的设计模式,但由…...
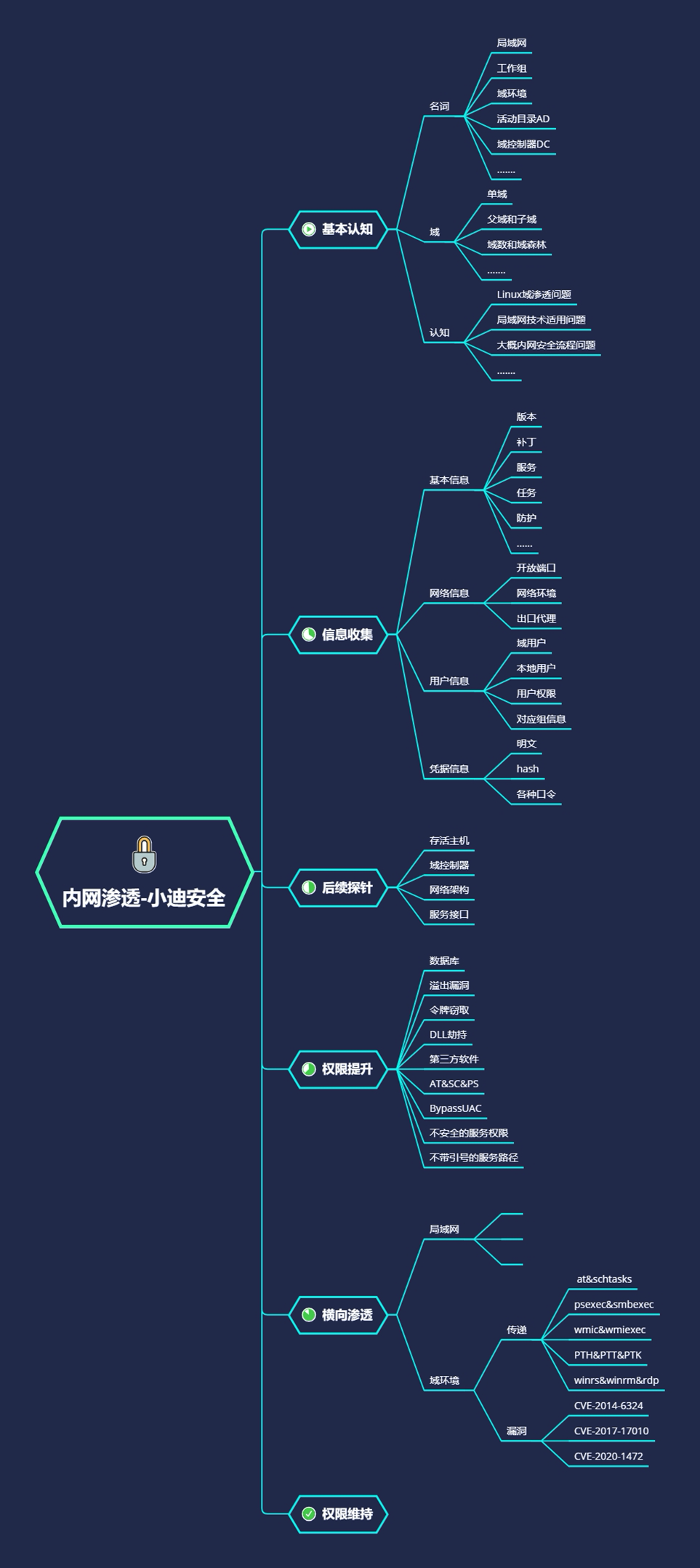
67 内网安全-域横向smbwmi明文或hash传递
#知识点1: windows2012以上版本默认关闭wdigest,攻击者无法从内存中获取明文密码windows2012以下版本如安装KB2871997补丁,同样也会导致无法获取明文密码针对以上情况,我们提供了4种方式解决此类问题 1.利用哈希hash传递(pth,ptk等…...

面向对象(类/继承/封装/多态)详解
简介: 面向对象编程(Object-Oriented Programming,OOP)是一种广泛应用于软件开发的编程范式。它基于一系列核心概念,包括类、继承、封装和多态。在这篇详细的解释中,我们将探讨这些概念,并说明它们如何在P…...

【Python机器学习】零基础掌握GradientBoostingRegressor集成学习
如何精准预测房价? 当人们提到房价预测时,很多人可能会想到房地产经纪人或专业的评估师。但是,有没有一种更科学、更精确的方法来预测房价呢?答案是有的,这就要用到机器学习中的一种算法——梯度提升回归(Gradient Boosting Regressor)。 假设现在有一组房屋数据,包括…...

【tio-websocket】12、应用层包—Packet
Packet 介绍 Packet 是用于表述业务数据结构的,我们通过继承 Packet 来实现自己的业务数据结构,对于各位而言,把 Packet 看作是一个普通的 VO 对象即可。 public class Packet implements java.io.Serializable, Cloneable {private static Logger log = LoggerFac…...
OpenCV官方教程中文版 —— 模板匹配
OpenCV官方教程中文版 —— 模板匹配 前言一、原理二、OpenCV 中的模板匹配三、多对象的模板匹配 前言 在本节我们要学习: 使用模板匹配在一幅图像中查找目标 函数:cv2.matchTemplate(),cv2.minMaxLoc() 一、原理 模板匹配是用来在一副大…...
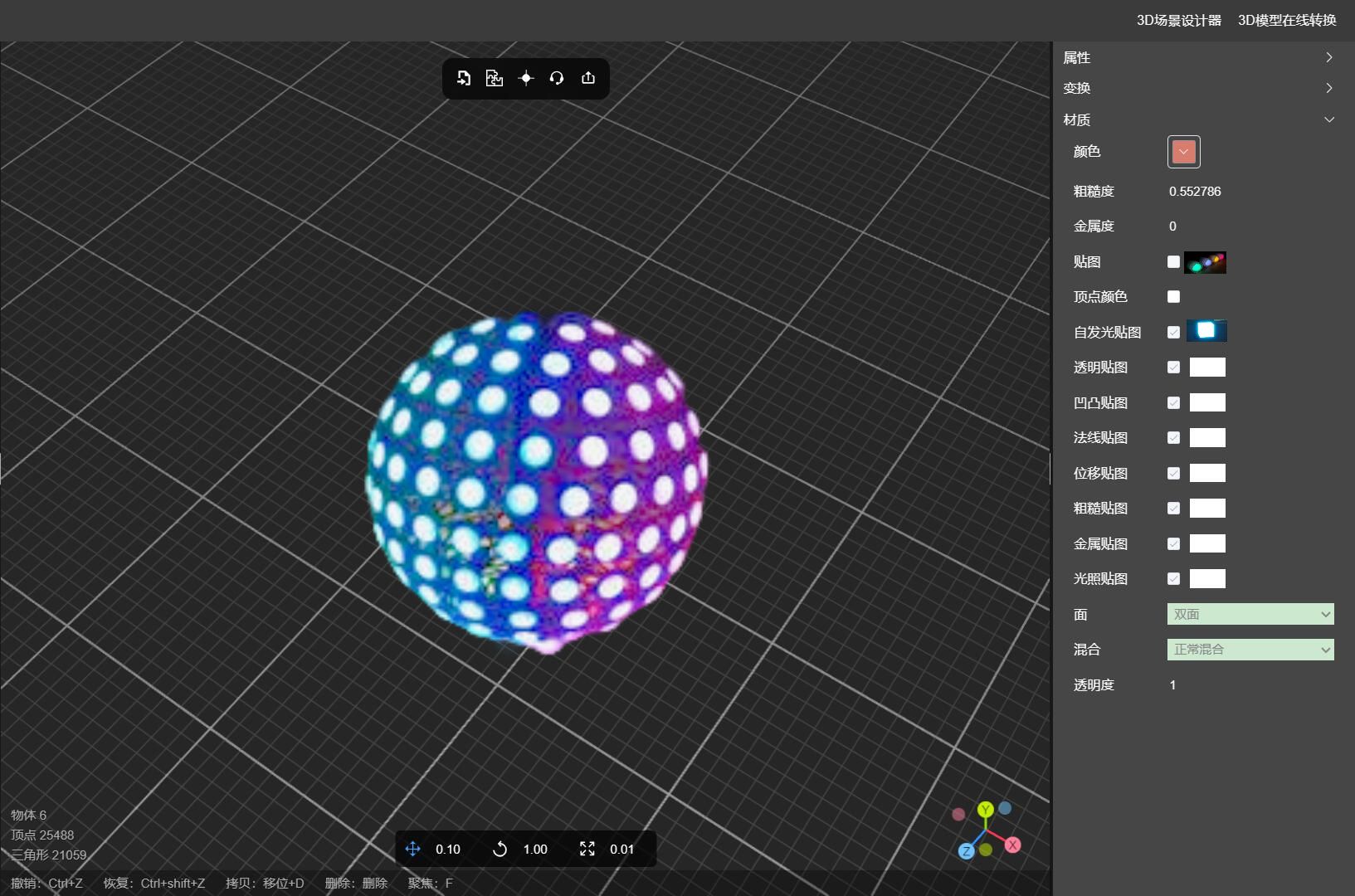
如何为3D模型设置自发光材质?
1、自发光贴图的原理 自发光贴图是一种纹理贴图,用于模拟物体自发光的效果。其原理基于光的发射和反射过程。 在真实世界中,物体自发光通常是由于其本身具有能够产生光的属性,如荧光物质、发光材料或光源本身。为了在计算机图形中模拟这种效…...
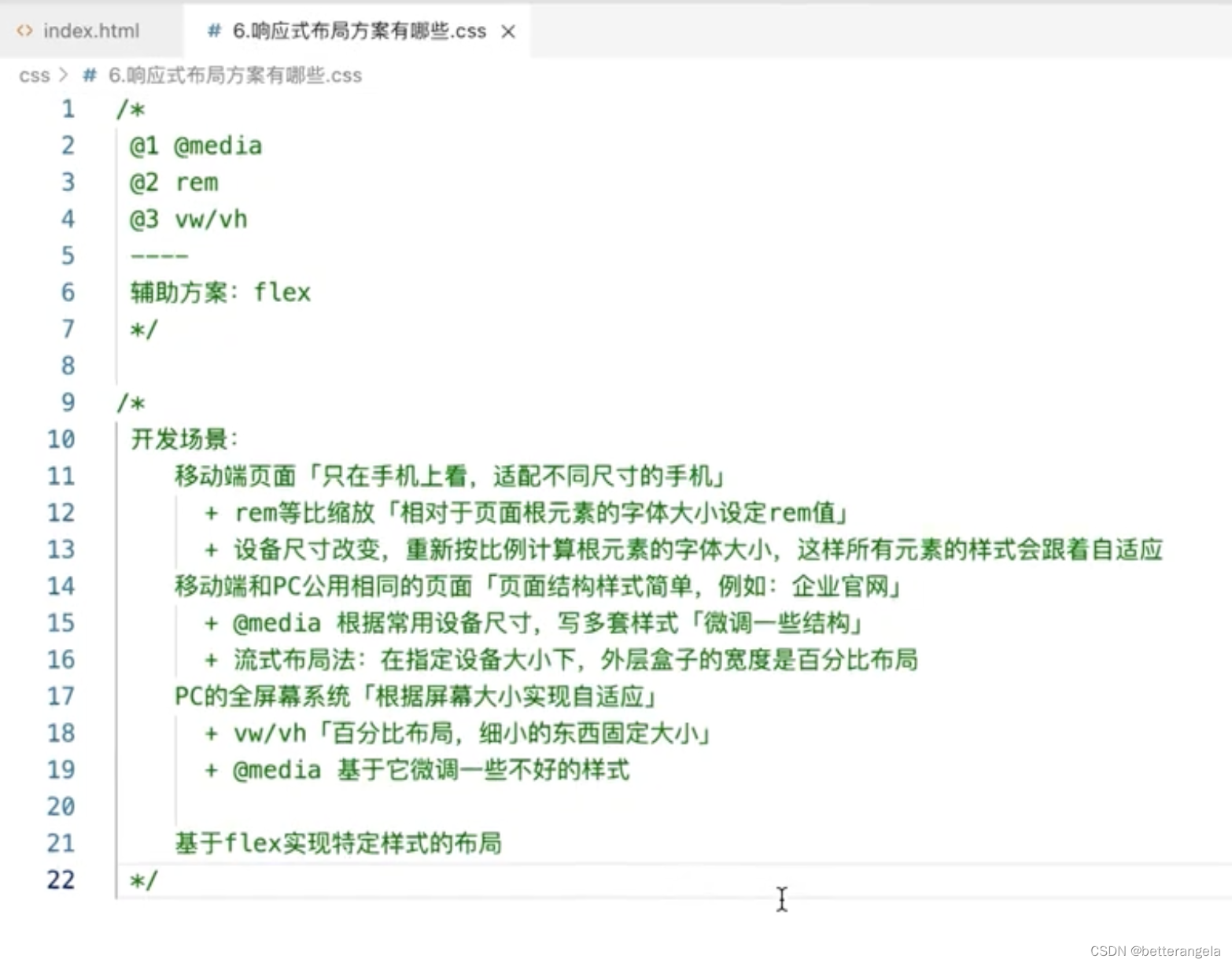
UI组件库基础
UI组件库 全局组件* 全局注册组件 & 并且使用了require.context 模块化编程 & webpack打包 const install(Vue)>{const contextrequire.context(.,true,/\.vue$/)context.keys().forEach(fileName>{const modulecontext(fileName)Vue.component(module.default.n…...
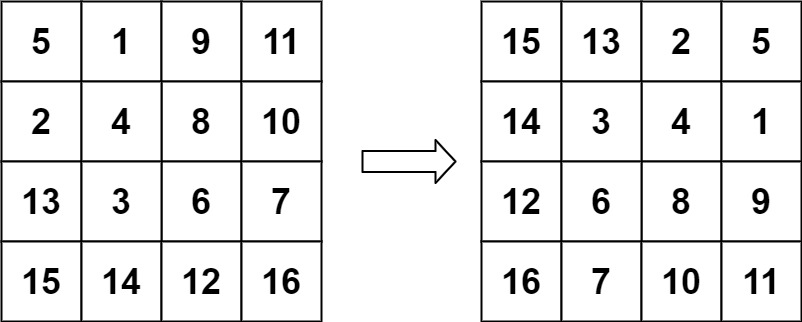
数据结构与算法之矩阵: Leetcode 48. 旋转矩阵 (Typescript版)
旋转图像 https://leetcode.cn/problems/rotate-image/ 描述 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 示例 1 输入&…...
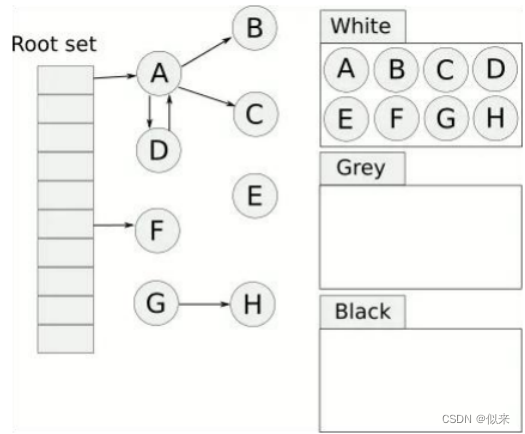
大厂面试题-JVM中的三色标记法是什么?
目录 问题分析 问题答案 问题分析 三色标记法是Java虚拟机(JVM)中垃圾回收算法的一种,主要用来标记内存中存活和需要回收的对象。 它的好处是,可以让JVM不发生或仅短时间发生STW(Stop The World),从而达到清除JVM内存垃圾的目的ÿ…...
Leetcode—121.买卖股票的最佳时机【简单】
2023每日刷题(十一) Leetcode—17.电话号码的字母组合 枚举法题解 参考自灵茶山艾府 枚举法实现代码 int maxProfit(int* prices, int pricesSize){int i;int max 0;int minPrice prices[0];for(i 1; i < pricesSize; i) {int tmp prices[i] -…...
【云原生】portainer管理多个独立docker服务器
目录 一、portainer简介 二、安装Portainer 1.1 内网环境下: 1.1.1 方式1:命令行运行 1.1.2 方式2:通过compose-file来启动 2.1 配置本地主机(node-1) 3.1 配置其他主机(被node-1管理的节点服务器&…...

Command集合
Command集合 mysql相关命令 查看mysql的状态 sudo netstat -tap | grep mysql 启动mysql sudo service mysql start 停止mysql sudo service mysql stop 重启mysql sudo service mysql restart 指定端口号,客户端连接mysql sudo mysql -h127.0.0.1 -uroot -p red…...
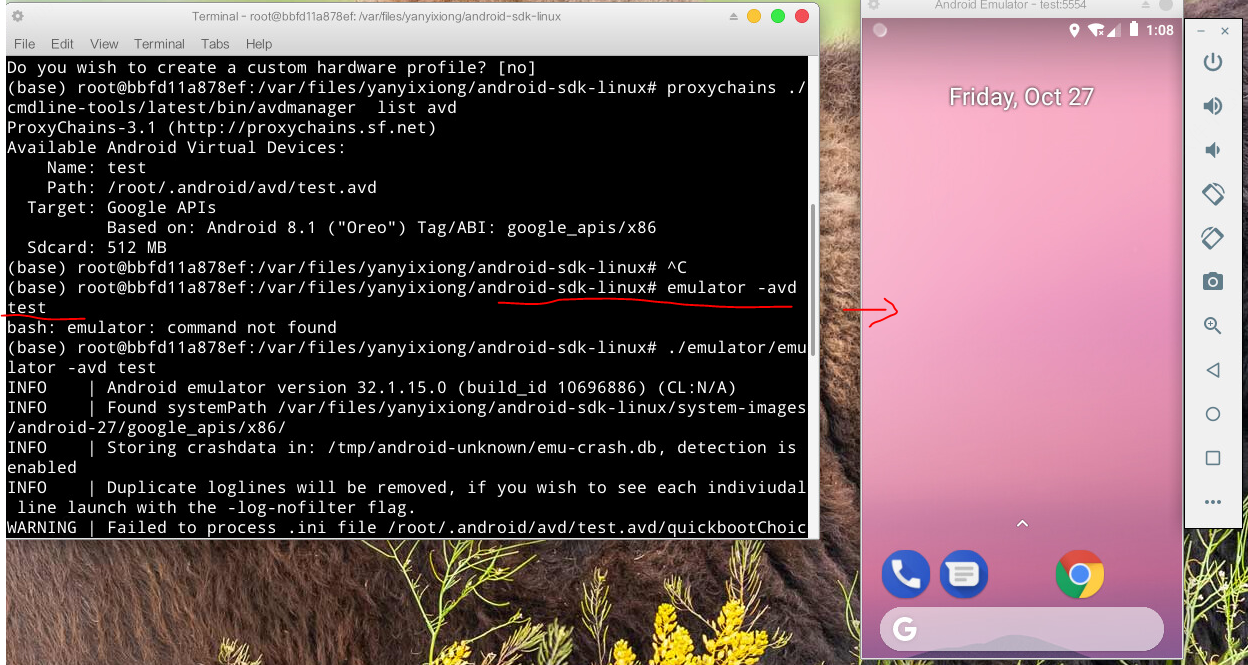
【QT开发(17)】2023-QT 5.14.2实现Android开发
1、简介 搭建Qt For Android开发环境需要安装的软件有: JAVA SDK (jdk 有apt install 安装) Android SDK Android NDKQT官网的介绍: Different Qt versions depend on different NDK versions, as listed below: Qt versionNDK…...
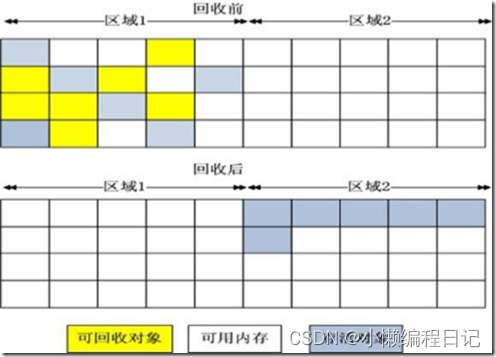
JVM相关面试题(每日一练)
1. 什么是垃圾回收机制? 垃圾收集 Garbage Collection 通常被称为“GC”,它诞生于1960年 MIT 的 Lisp 语言,经过半个多世纪,目前已经十分成熟了。 jvm 中,程序计数器、虚拟机栈、本地方法栈都是随线程而生随线程而灭&a…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
