当前位置： 首页 > news >正文

【Python机器学习】零基础掌握GradientBoostingRegressor集成学习

news 2026/2/9 21:01:34

如何精准预测房价？

当人们提到房价预测时，很多人可能会想到房地产经纪人或专业的评估师。但是，有没有一种更科学、更精确的方法来预测房价呢？答案是有的，这就要用到机器学习中的一种算法——梯度提升回归（Gradient Boosting Regressor）。

假设现在有一组房屋数据，包括房屋面积、楼层、距离市中心的距离和建造年份等信息。目标是通过这些信息来精准预测房屋的销售价格。

面积（平方米）楼层距离市中心（km）建造年份销售价格（万元）
90252005300
110332010400
80172000250
120422015450
100242008350
……………

对于这样的问题，梯度提升回归是一个很好的选择。它可以在多个弱预测模型的基础上，逐步构建一个强预测模型，从而更精准地预测房价。

梯度提升回归是一种集成学习方法，它结合了多个弱预测模型，通过逐步优化，构建一个强大的预测模型。它不仅用于房价

相关文章：

【Python机器学习】零基础掌握GradientBoostingRegressor集成学习

如何精准预测房价？ 当人们提到房价预测时，很多人可能会想到房地产经纪人或专业的评估师。但是，有没有一种更科学、更精确的方法来预测房价呢？答案是有的，这就要用到机器学习中的一种算法——梯度提升回归（Gradient Boosting Regressor）。 假设现在有一组房屋数据，包括…...

编程日记 2023/10/28 11:07:44

【tio-websocket】12、应用层包—Packet

Packet 介绍 Packet 是用于表述业务数据结构的，我们通过继承 Packet 来实现自己的业务数据结构，对于各位而言，把 Packet 看作是一个普通的 VO 对象即可。 public class Packet implements java.io.Serializable, Cloneable {private static Logger log = LoggerFac…...

编程日记 2023/10/28 11:06:43

OpenCV官方教程中文版 —— 模板匹配

OpenCV官方教程中文版 —— 模板匹配 前言一、原理二、OpenCV 中的模板匹配三、多对象的模板匹配 前言 在本节我们要学习： 使用模板匹配在一幅图像中查找目标 函数：cv2.matchTemplate()，cv2.minMaxLoc() 一、原理 模板匹配是用来在一副大…...

编程日记 2023/10/28 11:05:42

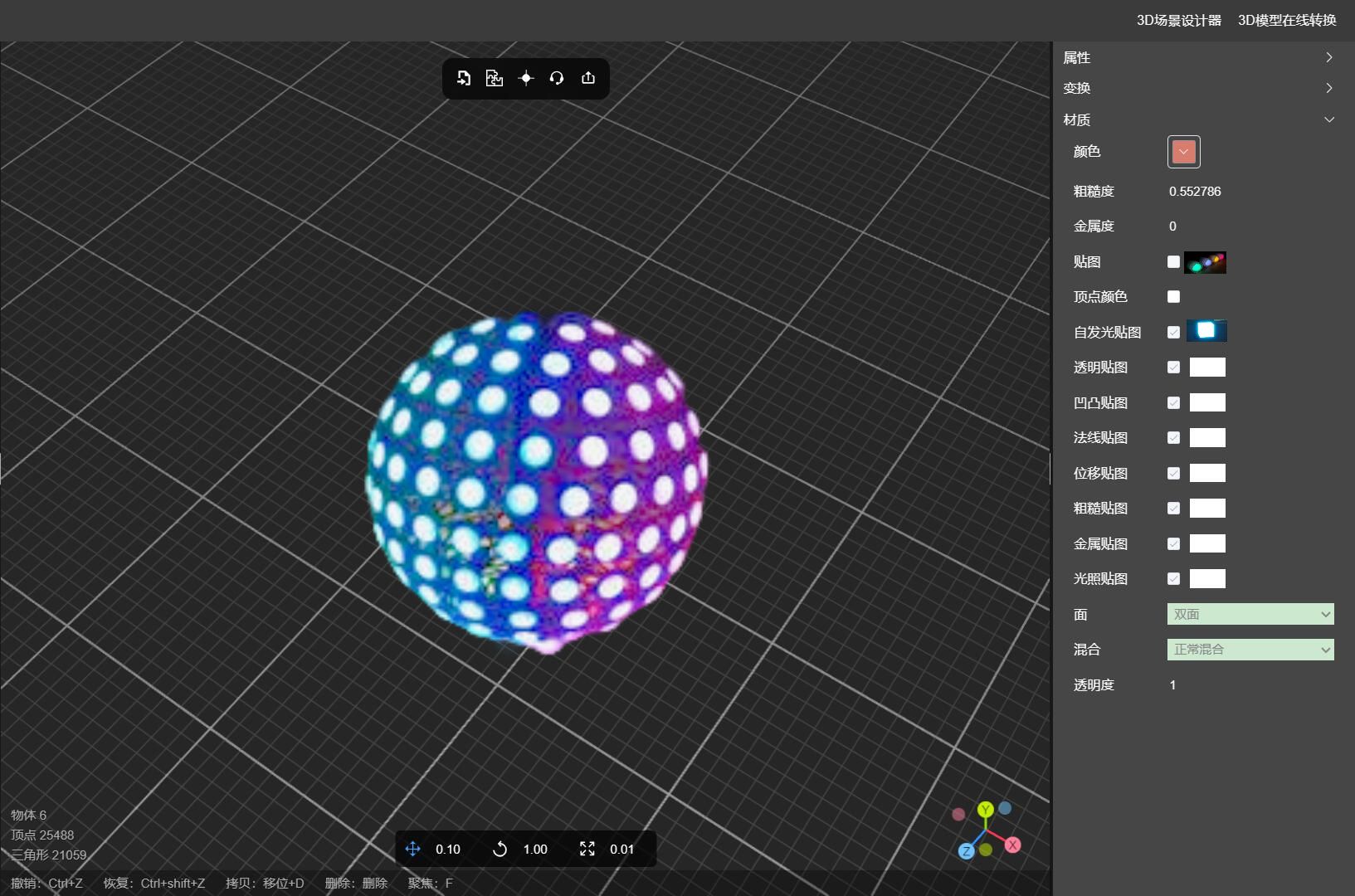
如何为3D模型设置自发光材质？

1、自发光贴图的原理 自发光贴图是一种纹理贴图，用于模拟物体自发光的效果。其原理基于光的发射和反射过程。 在真实世界中，物体自发光通常是由于其本身具有能够产生光的属性，如荧光物质、发光材料或光源本身。为了在计算机图形中模拟这种效…...

编程日记 2023/10/28 11:04:40

UI组件库基础

UI组件库 全局组件* 全局注册组件 & 并且使用了require.context 模块化编程 & webpack打包 const install(Vue)>{const contextrequire.context(.,true,/\.vue$/)context.keys().forEach(fileName>{const modulecontext(fileName)Vue.component(module.default.n…...

编程日记 2023/10/28 11:03:39

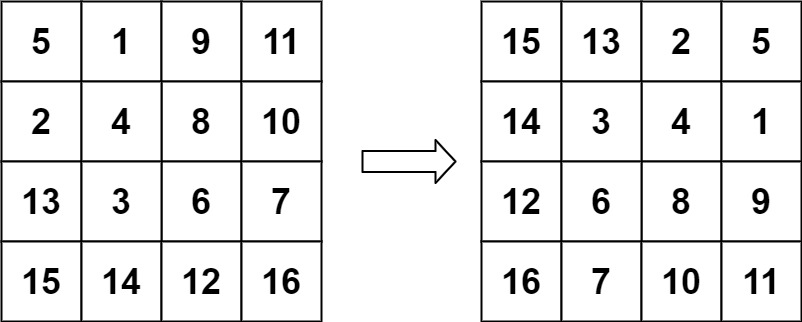
数据结构与算法之矩阵: Leetcode 48. 旋转矩阵 (Typescript版)

旋转图像 https://leetcode.cn/problems/rotate-image/ 描述 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 示例 1 输入&…...

编程日记 2023/10/28 11:02:38

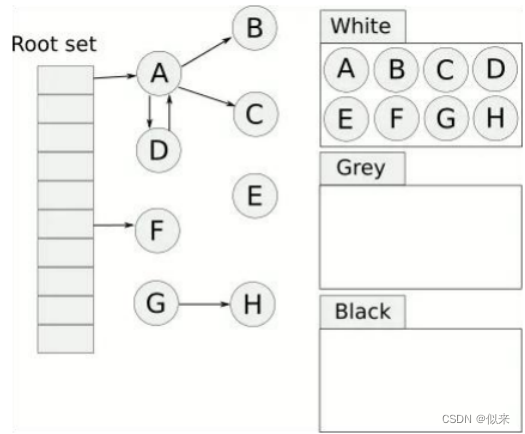
大厂面试题-JVM中的三色标记法是什么？

目录 问题分析 问题答案 问题分析 三色标记法是Java虚拟机(JVM)中垃圾回收算法的一种，主要用来标记内存中存活和需要回收的对象。 它的好处是，可以让JVM不发生或仅短时间发生STW(Stop The World)，从而达到清除JVM内存垃圾的目的&#xff…...

编程日记 2023/10/28 11:01:37

Leetcode—121.买卖股票的最佳时机【简单】

2023每日刷题&#xff08;十一&#xff09; Leetcode—17.电话号码的字母组合 枚举法题解 参考自灵茶山艾府 枚举法实现代码 int maxProfit(int* prices, int pricesSize){int i;int max 0;int minPrice prices[0];for(i 1; i < pricesSize; i) {int tmp prices[i] -…...

编程日记 2023/10/28 10:59:35

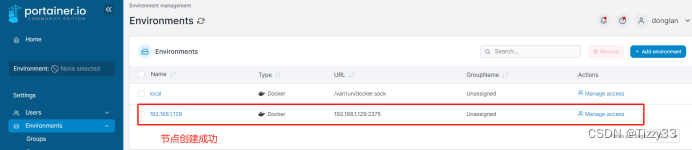
【云原生】portainer管理多个独立docker服务器

目录 一、portainer简介 二、安装Portainer 1.1 内网环境下&#xff1a; 1.1.1 方式1&#xff1a;命令行运行 1.1.2 方式2&#xff1a;通过compose-file来启动 2.1 配置本地主机&#xff08;node-1&#xff09; 3.1 配置其他主机&#xff08;被node-1管理的节点服务器&…...

编程日记 2023/10/28 10:58:34

Command集合

Command集合 mysql相关命令 查看mysql的状态 sudo netstat -tap | grep mysql 启动mysql sudo service mysql start 停止mysql sudo service mysql stop 重启mysql sudo service mysql restart 指定端口号&#xff0c;客户端连接mysql sudo mysql -h127.0.0.1 -uroot -p red…...

编程日记 2023/10/28 10:57:33

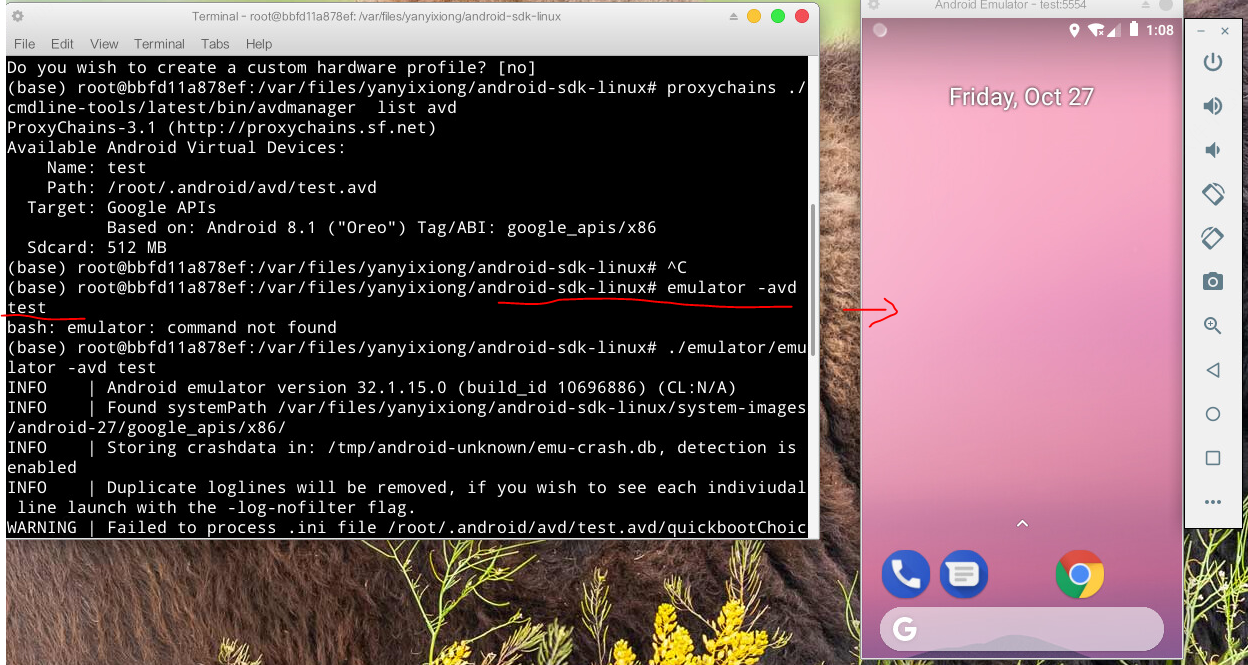
【QT开发（17）】2023-QT 5.14.2实现Android开发

1、简介 搭建Qt For Android开发环境需要安装的软件有&#xff1a; JAVA SDK &#xff08;jdk 有apt install 安装&#xff09; Android SDK Android NDKQT官网的介绍&#xff1a; Different Qt versions depend on different NDK versions, as listed below: Qt versionNDK…...

编程日记 2023/10/28 10:56:32

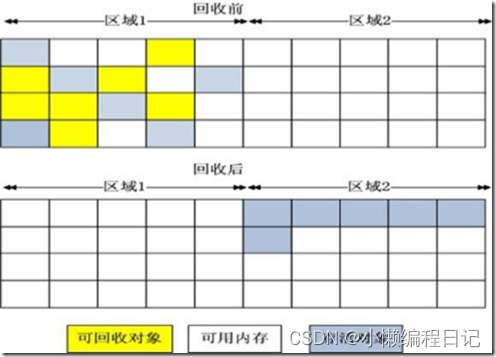
JVM相关面试题（每日一练）

1. 什么是垃圾回收机制&#xff1f; 垃圾收集 Garbage Collection 通常被称为“GC”&#xff0c;它诞生于1960年 MIT 的 Lisp 语言&#xff0c;经过半个多世纪&#xff0c;目前已经十分成熟了。 jvm 中&#xff0c;程序计数器、虚拟机栈、本地方法栈都是随线程而生随线程而灭&a…...

编程日记 2023/10/28 10:55:30

OpenCV 相机相关函数

一、变换参数矩阵的求解 1. 计算三个二维点对之间的仿射变换矩阵&#xff1a;getAffineTransform() 2. 计算多个二维点对之间的最优放射变换矩阵&#xff08;误差最小准则&#xff09;&#xff1a;estimateRigidTransform();或者findHomography(); 3. 计算四个二维点对之间的…...

编程日记 2023/10/28 10:54:29

微信小程序之投票管理

前言 对于会议管理模块&#xff0c;必不可少的当然就是我们的投票管理&#xff0c;实现真正意义上的无纸化办公&#xff0c;本期博客为大家介绍会议管理模块&#xff0c;包括发布投票及查看各类投票的状态 所用技术点 MyBatis、SpringMVC、VentUI MyBatis和SpringMVC在博客主…...

编程日记 2023/10/28 10:53:27

23种设计模式【创建型模式】详细介绍之【建造者模式】

建造者模式&#xff1a;构建复杂对象的精妙设计 设计模式的分类和应用场景总结建造者模式&#xff1a;构建复杂对象的精妙设计建造者模式的核心思想建造者模式的参与者Java示例&#xff1a;建造者模式 设计模式的分类和应用场景总结 可以查看专栏设计模式&#xff1a;设计模式 …...

编程日记 2023/10/28 10:52:27

[量化投资-学习笔记002]Python+TDengine从零开始搭建量化分析平台-MA均线的多种实现方式

MA 均线时最基本的技术指标&#xff0c;也是最简单&#xff0c;最不常用的&#xff08;通常使用EMA、SMA&#xff09;。 以下用两种不同的计算方法和两种不同的画图方法进行展示和说明。 MA 均线指标公式 MA (N)(C1 C2 C3 …C N )/N目录 方式一1.SQL 直接查询均值2.使用 pyp…...

编程日记 2023/10/28 10:50:25

c语言 判断两个文件是否相同

使用strcmp比较&#xff1a; #include <stdio.h> #include <string.h>int Compare(const char * file1, const char* file2) {FILE* f1, * f2;int size1, size2;unsigned char buffer1[1024], buffer2[1024];f1 fopen(file1, "rb");f2 fopen(file2, &…...

编程日记 2023/10/28 10:49:23

【2021集创赛】Arm杯三等奖：基于FPGA的人脸检测SoC设计

本作品参与极术社区组织的有奖征集|秀出你的集创赛作品风采,免费电子产品等你拿~活动。 团队介绍 参赛单位&#xff1a;合肥工业大学 队伍名称&#xff1a;芯创之家 指导老师&#xff1a;邓红辉、尹勇生 参赛杯赛&#xff1a;Arm杯 参赛人员&#xff1a;王亮 李嘉燊 金京 获奖情…...

编程日记 2023/10/28 10:48:22

Java电商平台 - API 接口设计之 token、timestamp、sign 具体架构与实现|电商API接口接入

一&#xff1a;token 简介 Token&#xff1a;访问令牌access token, 用于接口中, 用于标识接口调用者的身份、凭证&#xff0c;减少用户名和密码的传输次数。一般情况下客户端(接口调用方)需要先向服务器端申请一个接口调用的账号&#xff0c;服务器会给出一个appId和一个key, …...

编程日记 2023/10/28 10:47:21

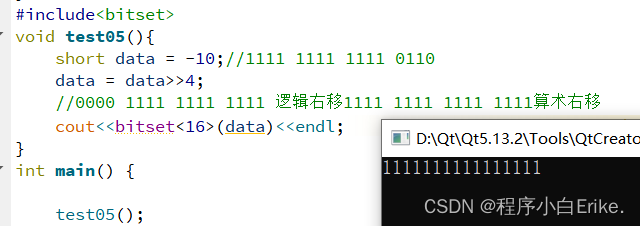
【带头学C++】----- 1.基础知识 ---- 1.23 运算符概述

1.23 运算符概述 运算符&#xff0c;在数学中常见的加减乘除之类的符号&#xff0c;那么在C在编程语言中呢&#xff0c;将使用特定的符号或标记对操作数进行操作以生成结果。用算术运算符将运算对象(也称操作数)连接起来的、符合C 语法规则的式子&#xff0c;称为C 算术表达式运…...

编程日记 2023/10/28 10:46:20

Vue记事本应用实现教程

文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展&#xff1a;显示创建时间8. 功能扩展&#xff1a;记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

编程新知 2025/9/20 5:20:12

Debian系统简介

目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版&#xff…...

编程新知 2026/2/1 13:41:09

Frozen-Flask ：将 Flask 应用“冻结”为静态文件

Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是&#xff1a;将一个 Flask Web 应用生成成纯静态 HTML 文件&#xff0c;从而可以部署到静态网站托管服务上&#xff0c;如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

编程新知 2025/12/5 20:57:13

Web 架构之 CDN 加速原理与落地实践

文章目录 一、思维导图二、正文内容&#xff08;一&#xff09;CDN 基础概念1. 定义2. 组成部分 &#xff08;二&#xff09;CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 &#xff08;三&#xff09;CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 &#xf…...

编程新知 2025/9/13 16:17:01

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数

高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数 在软件开发中，单例模式（Singleton Pattern）是一种常见的设计模式，确保一个类仅有一个实例，并提供一个全局访问点。在多线程环境下，实现单例模式时需要注意线程安全问题，以防止多个线程同时创建实例，导致…...

编程新知 2025/11/25 19:50:27

基于Java+MySQL实现（GUI）客户管理系统

客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息&#xff0c;对客户进行统一管理&#xff0c;可以把所有客户信息录入系统&#xff0c;进行维护和统计功能。可通过文件的方式保存相关录入数据&#xff0c;对…...

编程新知 2026/1/25 10:12:06

IP如何挑？2025年海外专线IP如何购买？

你花了时间和预算买了IP&#xff0c;结果IP质量不佳&#xff0c;项目效率低下不说&#xff0c;还可能带来莫名的网络问题&#xff0c;是不是太闹心了&#xff1f;尤其是在面对海外专线IP时&#xff0c;到底怎么才能买到适合自己的呢&#xff1f;所以&#xff0c;挑IP绝对是个技…...

编程新知 2026/1/28 3:04:35

【分享】推荐一些办公小工具

1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由&#xff1a;大部分的转换软件需要收费&#xff0c;要么功能不齐全&#xff0c;而开会员又用不了几次浪费钱&#xff0c;借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

编程新知 2026/1/25 14:40:59

FFmpeg：Windows系统小白安装及其使用

一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】&#xff0c;注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录&#xff08;即exe所在文件夹&#xff09;加入系统变量…...

编程新知 2026/1/31 14:34:46

WPF八大法则：告别模态窗口卡顿

⚙️ 核心问题&#xff1a;阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程&#xff0c;导致后续逻辑无法执行&#xff1a; var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题&#xff1a…...

编程新知 2026/1/26 17:26:03