【go】两数求和
文章目录
- 题目
- 代码
- 解法2
- 代码仓库
题目
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
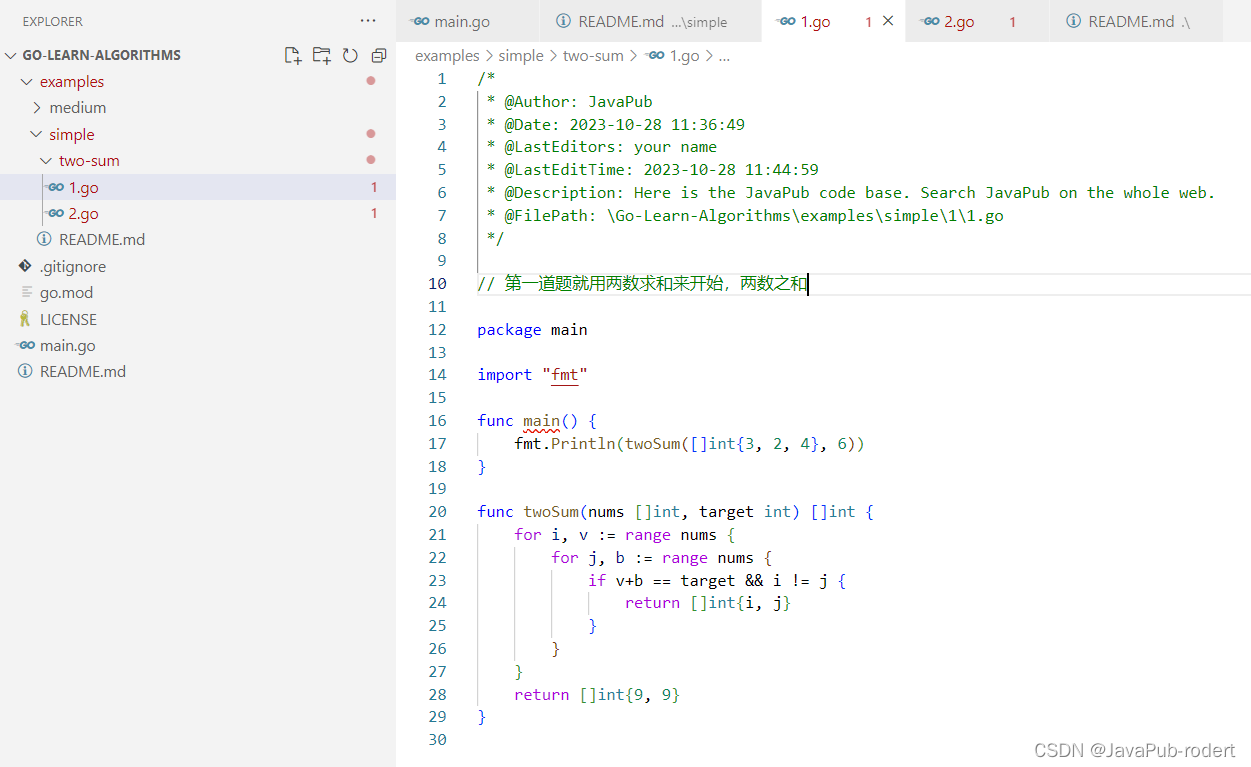
代码
/** @Author: JavaPub* @Date: 2023-10-28 11:36:49* @LastEditors: your name* @LastEditTime: 2023-10-28 11:44:59* @Description: Here is the JavaPub code base. Search JavaPub on the whole web.* @FilePath: \Go-Learn-Algorithms\examples\simple\1\1.go*/// 第一道题就用两数求和来开始,两数之和package mainimport "fmt"func main() {fmt.Println(twoSum([]int{3, 2, 4}, 6))
}func twoSum(nums []int, target int) []int {for i, v := range nums {for j, b := range nums {if v+b == target && i != j {return []int{i, j}}}}return []int{9, 9}
}解法2
package mainimport "fmt"func main() {fmt.Println(twoSumV2([]int{2, 7, 11, 15}, 9))
}func twoSumV2(nums []int, target int) []int {for i, x := range nums {for j := i + 1; j < len(nums); j++ {if x+nums[j] == target {return []int{i, j}}}}return nil
}代码仓库
https://github.com/Rodert/Go-Learn-Algorithms/tree/main/examples/simple/two-sum
相关文章:

【go】两数求和
文章目录 题目代码解法2 代码仓库 题目 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案…...

软考高项-成本管理
工具和技术 三点估算 通过考虑估算中的不确定性与风险,使用3种估算值来界定活动成本的近似区间,可以提高活动成本估算的准确性; 储备分析 为应对成本的不确定性,成本估算中可以包括应急储备。应急储备的管理方法: 将…...

24年FRM备考知识点以及一级公式表
FRM一级公示表以及备考知识点 链接:https://pan.baidu.com/s/17RpFF9OyfRk7FGtEQrxf3A?pwd1234 提取码:1234 FRM二级公示表以及备考知识点 链接:https://pan.baidu.com/s/175D05wV1p94dIfBZThutCQ?pwd1234 提取码:1234...
Spring Cloud学习:二【详细】
目录 Nacos的配置 Nacos的单机启动 服务注册 Nacos服务分级存储模型 优先访问同集群的服务 根据权重负载均衡 环境隔离Namespace Nacos调用流程 Nacos与Eureka注册对比 Nacos与Eureka的共同点 Nacos与Eureka的区别 Nacos配置管理 统一配置 配置自动刷新 多环境配…...

Unity的live2dgalgame多语言可配置剧情框架
这段代码用于读取表格 using System; using System.Collections; using System.Collections.Generic; using UnityEngine; using OfficeOpenXml; using System.IO; using UnityEngine.Networking; using UnityEngine.UI; using Random UnityEngine.Random;public class Plots…...

再畅通工程(最小生成树)
题目描述:还是畅通工程 某省调查乡村交通状况,得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可)&…...
前后端分离不可忽视的陷阱,深入剖析挑战,分享解决方案,助你顺利实施分离开发。
不管你设计的系统架构是怎么样,最后都是你的组织内的沟通结构胜出。这个观点一直在组织内不断地被证明,但也不断地被忽略。 前后端分离的利与弊 近几年,随着微服务架构风格的引入、前后端生态的快速发展、多端产品化的出现,前后…...

(四)库存超卖案例实战——优化redis分布式锁
前言 在上一节内容中,我们已经实现了使用redis分布式锁解决商品“超卖”的问题,本节内容是对redis分布式锁的优化。在上一节的redis分布式锁中,我们的锁有俩个可以优化的问题。第一,锁需要实现可重入,同一个线程不用重…...
【ROS入门】雷达、摄像头及kinect信息仿真以及显示
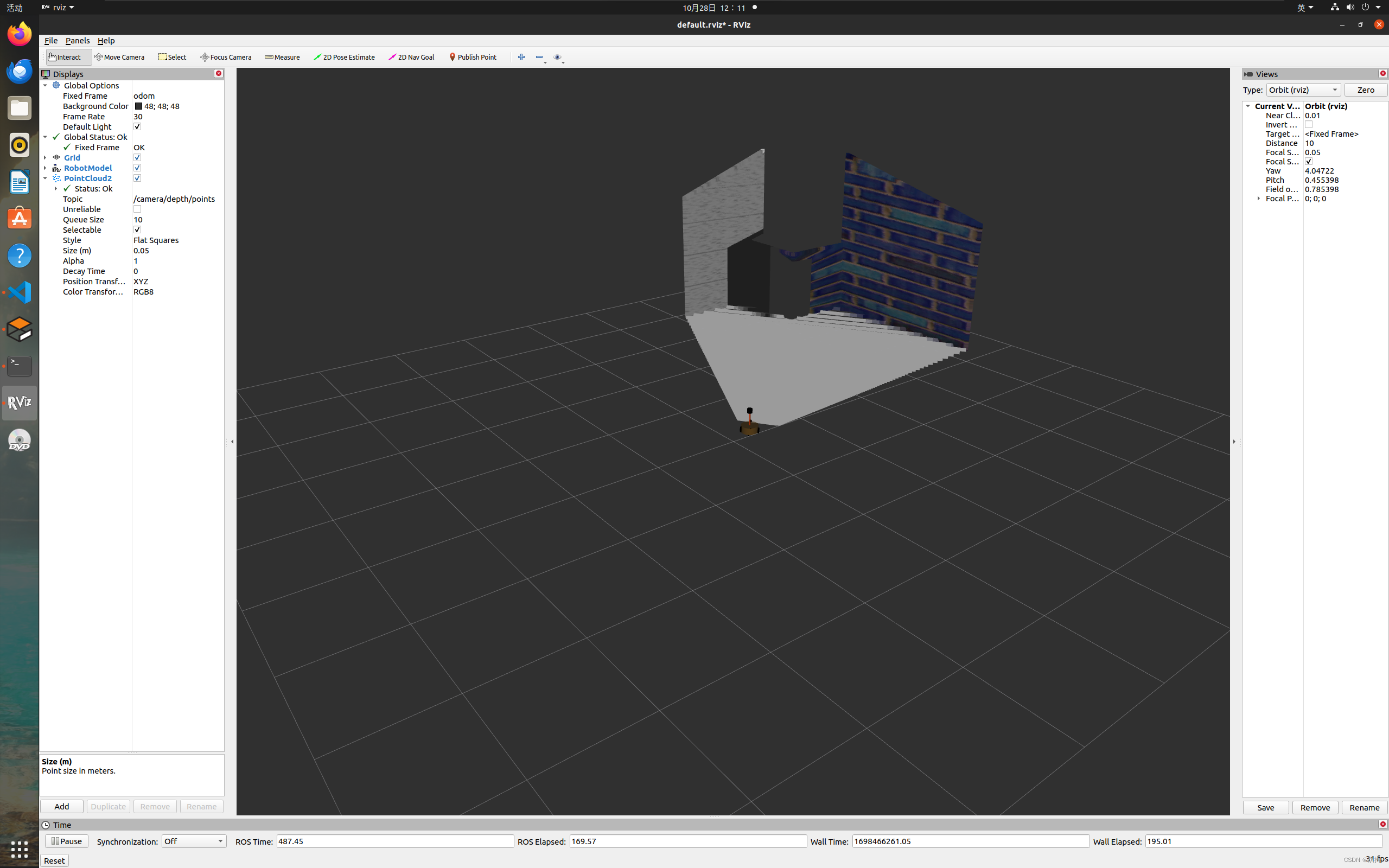
文章结构 雷达信息仿真以及显示Gazebo仿真雷达配置雷达传感器信息xacro文件集成启动仿真环境 Rviz显示雷达数据 摄像头信息仿真以及显示Gazebo仿真摄像头新建xacro文件,配置摄像头传感器信息xacro文件集成启动仿真环境 Rviz显示摄像头数据 kinect信息仿真以及显示Ga…...
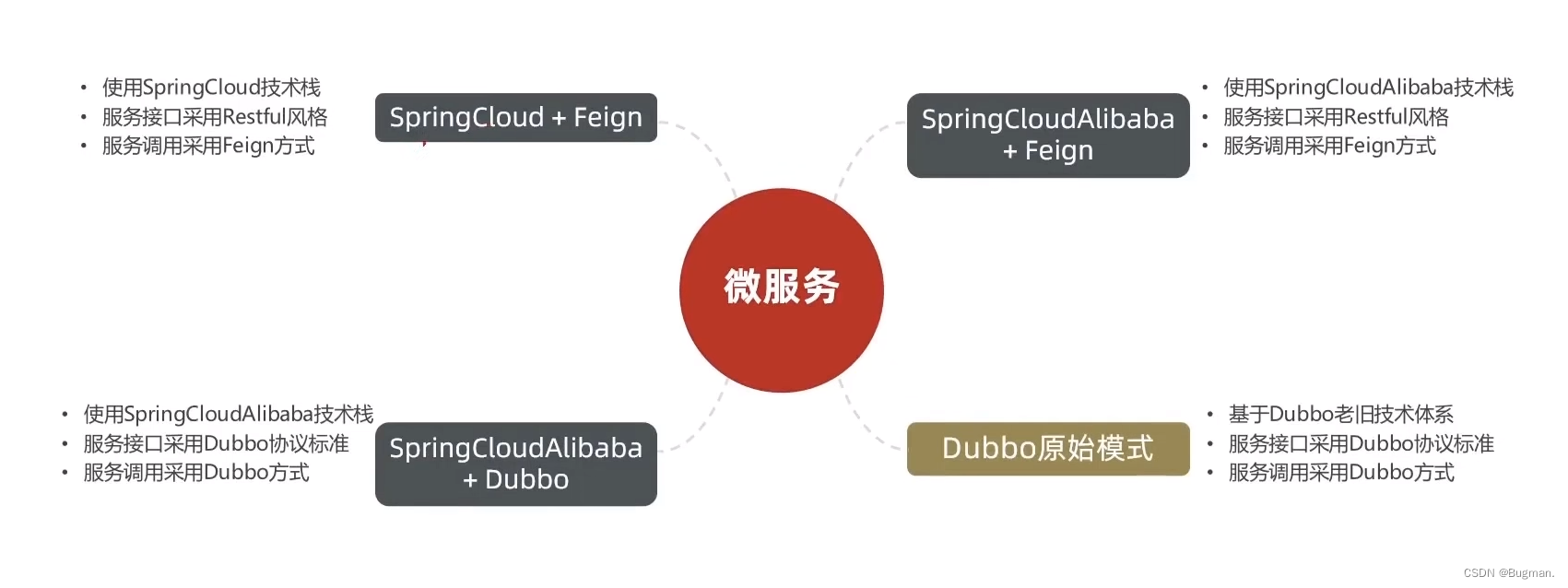
实用篇-认识微服务
一、服务架构演变 1. 单体架构 单体架构:将业务的所有功能集中在一个项目中开发,打成一个包部署 单体架构的优点: 架构简单部署成本低 单体架构的缺点: 耦合度高 2. 分布式架构 分布式架构: 根据业务功能对系…...

【产品运营】产品需求应该如何管理
产品项目在进行时经常会有一些需求需要实现,需求是产品更新迭代的动力,需求也是从用户诉求转化而来;在做需求管理时,我们需要判断一个需求的优先级等方面,对产品进行优化; 目录: 一、 为什么要…...
Linux 系统调用IO口,利用光标偏移实现文件复制
用系统调用IO函数实现从一个文件读取最后2KB数据并复制到另一个文件中,源文件以只读方式打开,目标文件以只写的方式打开,若目标文件不存在,可以创建并设置初始值为0664,写出相应代码,要对出错情况有一定的处…...

【原创】指针变量作为函数参数要点注意
指针变量作为函数参数要点注意(已写至笔记) 1传参指针不加*(main中函数) 2收参指针要加*(被main调用的函数) 3传参指针名可与收参指针名不同,不影响 4【问】如何看主函数中指针所指内容是否改变…...
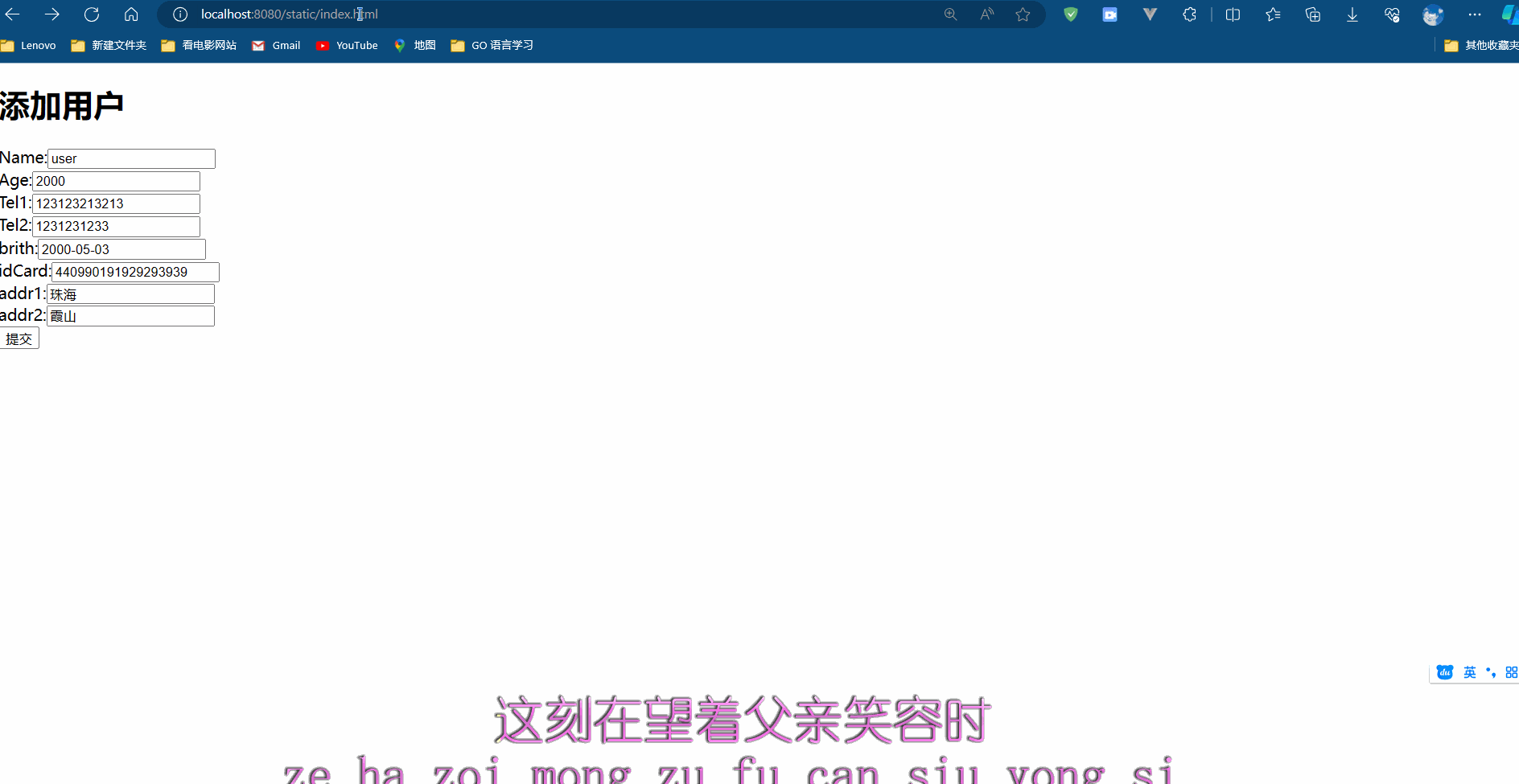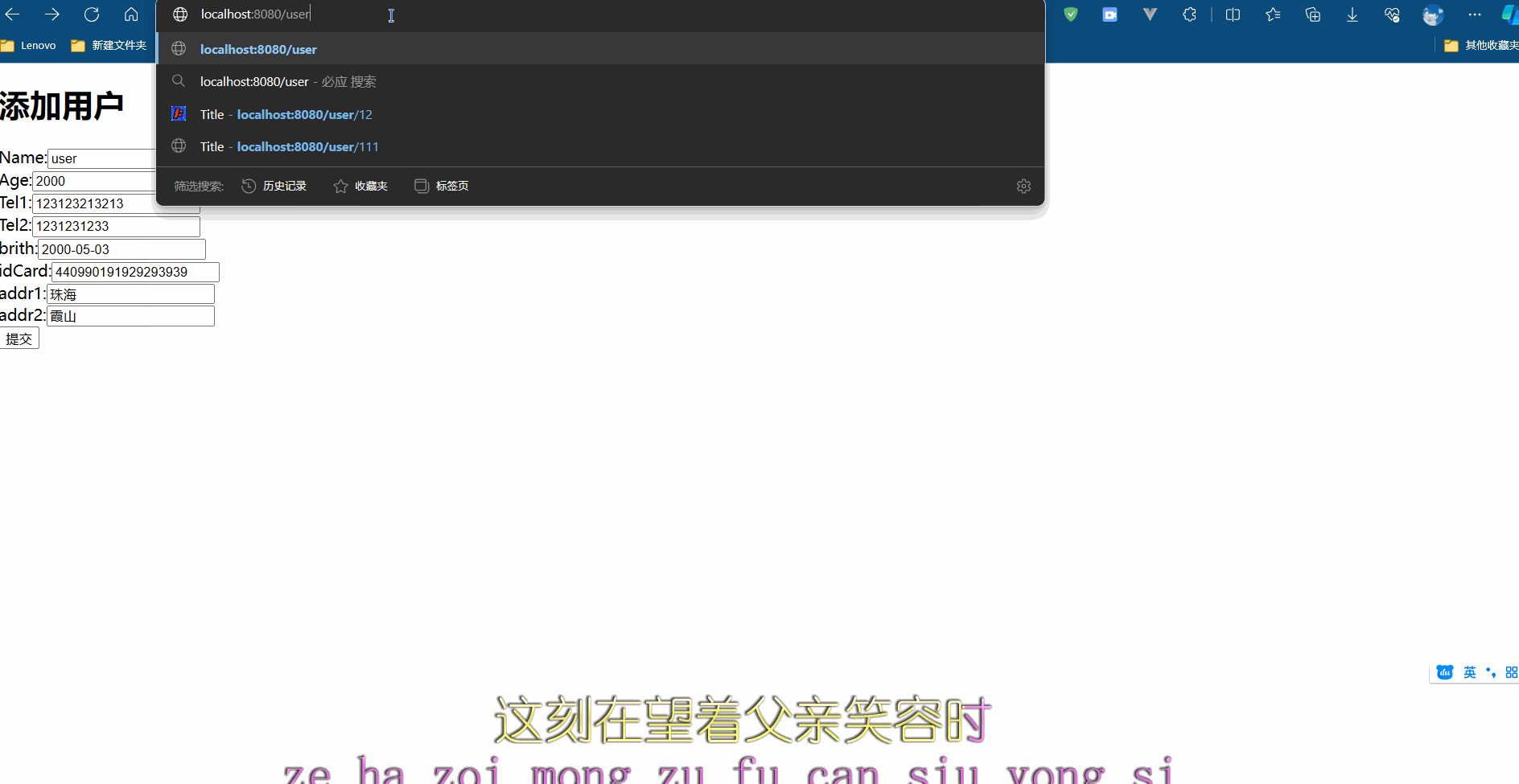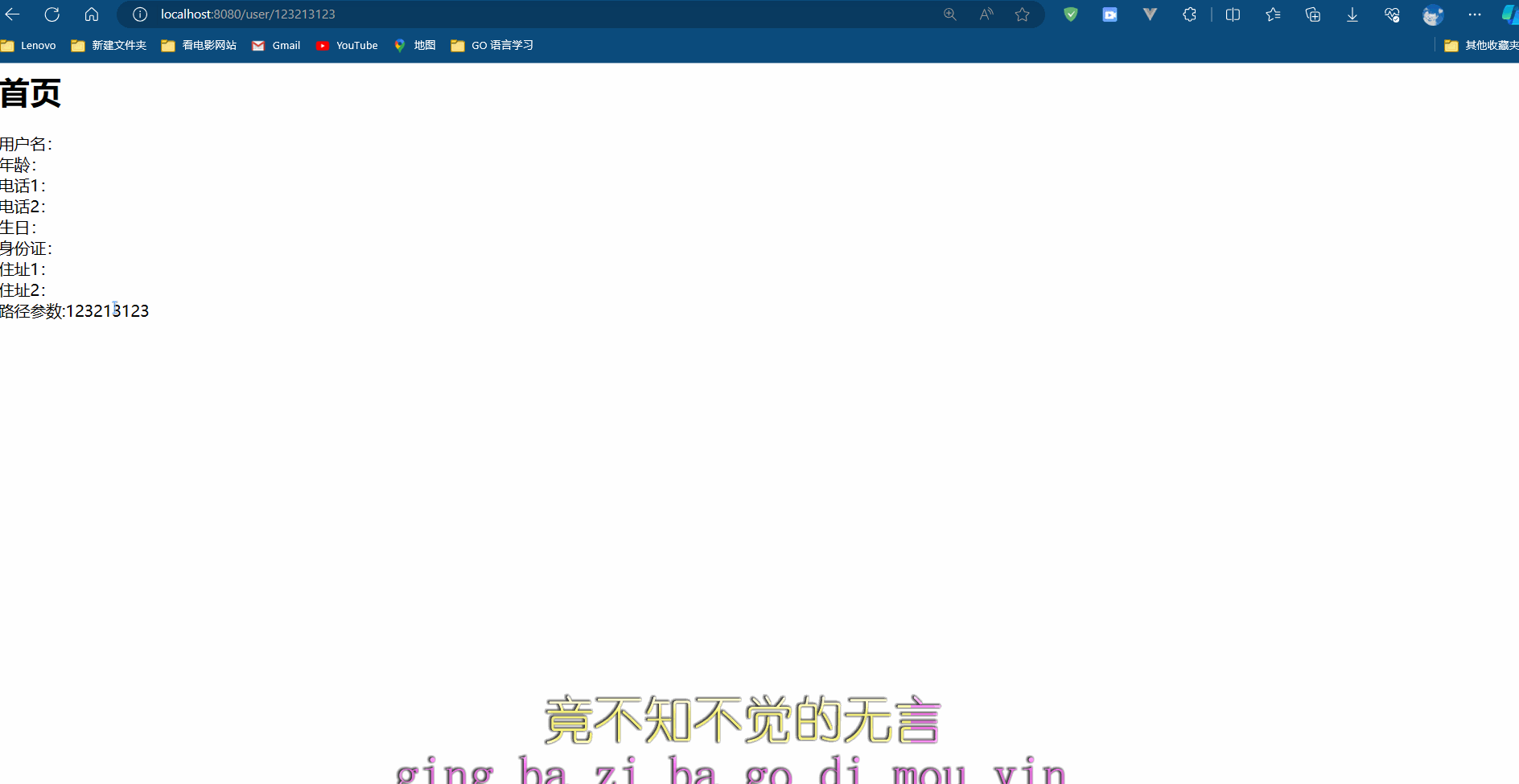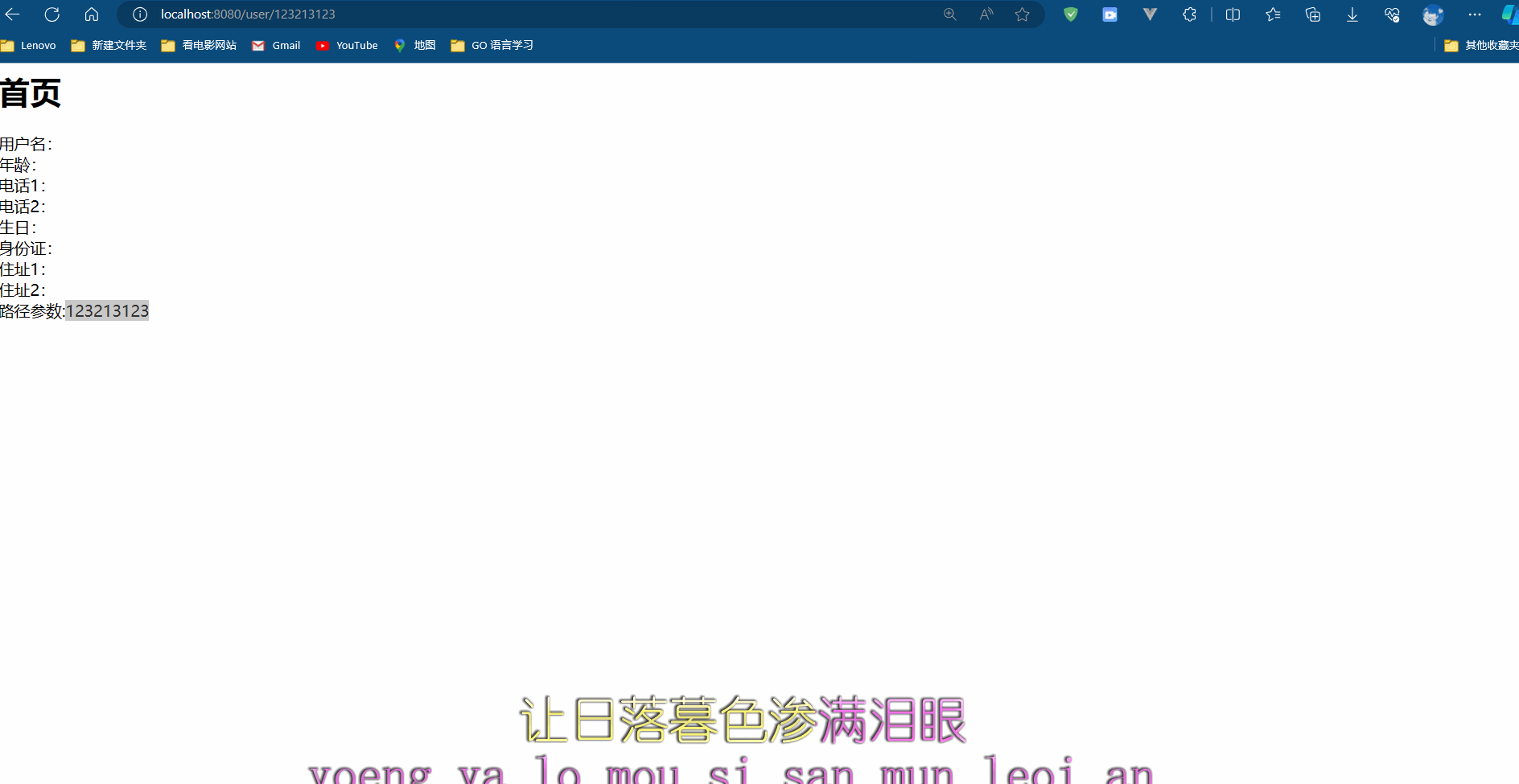
SpringMVC Day 04 : 数据绑定
前言 SpringMVC是一个非常流行的Java Web框架,它提供了很多方便的功能和工具来帮助我们构建高效、灵活的Web应用程序。其中,数据绑定就是SpringMVC中非常重要的一部分,它可以帮助我们方便地将请求参数绑定到Java对象上,从而简化了…...

2.3.1 协程设计原理与汇编实现
1.为什么要有协程? 同步的编程方式,异步的性能。同步编程时,我们需要等待io就绪。但是在协程这里,我们使用一种机制,当io需要等待时,就切到下一个io,之后当之前的io就绪时,再切换回来…...
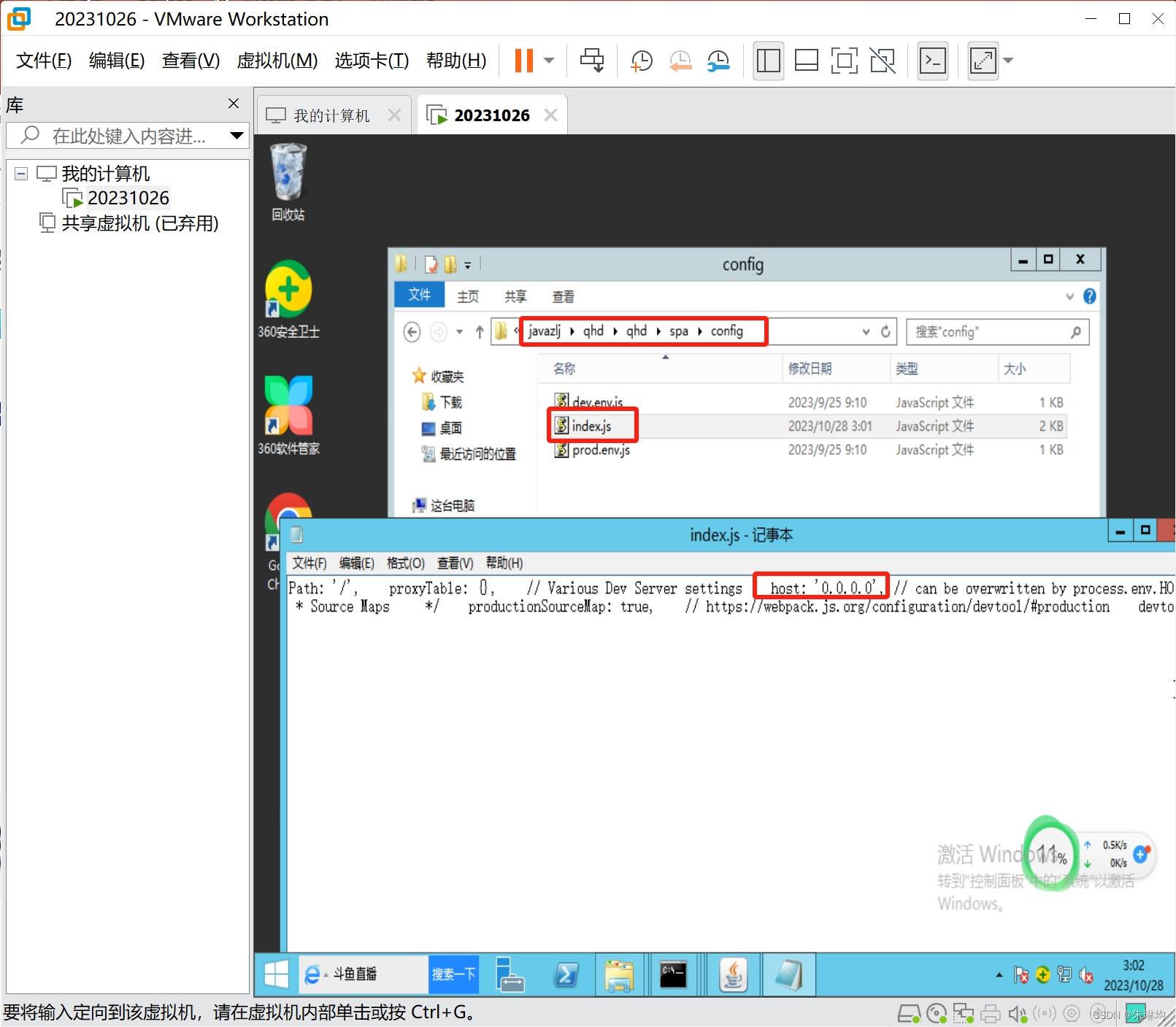
J2EE项目部署与发布(Windows版本)->会议OA单体项目Windows部署,spa前后端分离项目Windows部署
会议OA单体项目Windows部署spa前后端分离项目Windows部署 1.会议OA单体项目Windows部署(以实施的角度) 将项目放入webapp,项目能够访问: 首先拿到war包和数据库脚本,并检查是否有什么问题。 如何查看项目报错信息(当你…...

Lua脚本语言
1. 概念 Lua(发音为"loo-ah",葡萄牙语中的"lua"意为月亮)是一种轻量级的、高效的、可嵌入的脚本编程语言。官网Lua最初由巴西计算机科学家Roberto Ierusalimschy、Waldemar Celes和Luiz Henrique de Figueiredo于1993年开…...
函数和print()函数的区别)
cat()函数和print()函数的区别
目录 区别一: 区别二: cat、print函数都是输出函数。 区别一: cat()函数不能赋值; print()函数可以赋值。 x<-cat("hello world") //赋值 hello world x //cat函数无返回值 NULLy<-print("hello …...

宝塔面板安装Python和Flask(新版Python项目)
(一)宝塔面板的项目菜单,打开Python项目的“项目版本管理” 安装Python版本3.10.0。 会创建一个Python版本的文件夹www/server/pyproject_evn/versions/ 会创建一个Python虚拟环境的文件夹www/server/pyproject_evn/python_venv/ …...

火柴排队.
题意:给两列火柴,可以交换任意相邻的火柴,使得(ai-bi)^2的和最小,求最小交换次数。 分析:使得(ai-bi)^2的和最小,即a^2-2abb^2的和最小,那么使得2ab最大,就可…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
