NNDL:作业五
习题4-1
对于一个神经元![]() ,并使用梯度下降优化参数w时,如果输入x恒大于0,其收敛速度会比零均值化的输入更慢.
,并使用梯度下降优化参数w时,如果输入x恒大于0,其收敛速度会比零均值化的输入更慢.
证明:
激活函数以sigmoid为例。
神经元:有两层,线性层和激活层:y=w*x+b,然后y‘=sigmoid(y),也就是。
梯度下降:在激活函数的导数方向进行更新【因为梯度方向下降速度最快】。
零均值化:对于一个样本特征,可以使用如下公式实现零均值化处理:x_new = (x - x_mean) / N,使得特征数据之间具有可比性。同时零均值化是一种常用的数据正则化方法,可以有效地防止模型过拟合和提高模型训练效果。
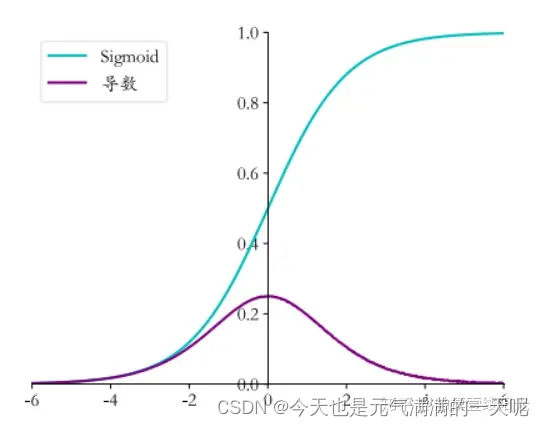
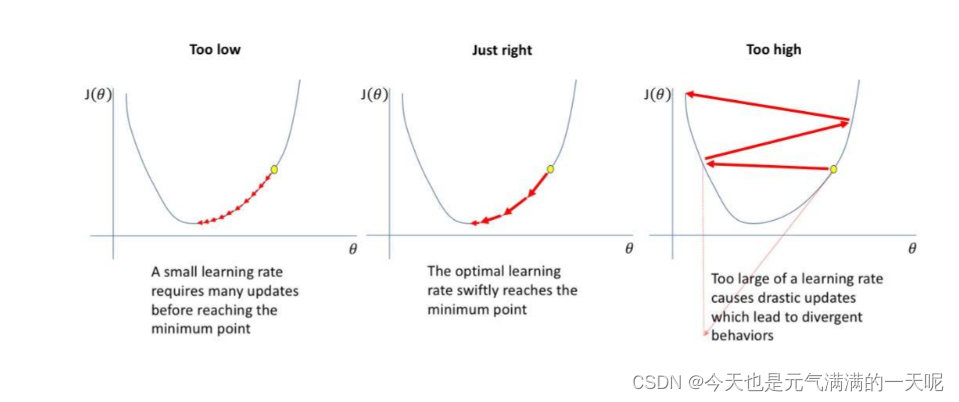
如上图所示,在激活函数的值为0时,导数最大,下降速度最快;两侧距离原点越远导数越小,下降速度越慢。 神经元对求导后的结果为
,由图可知
值大于0。
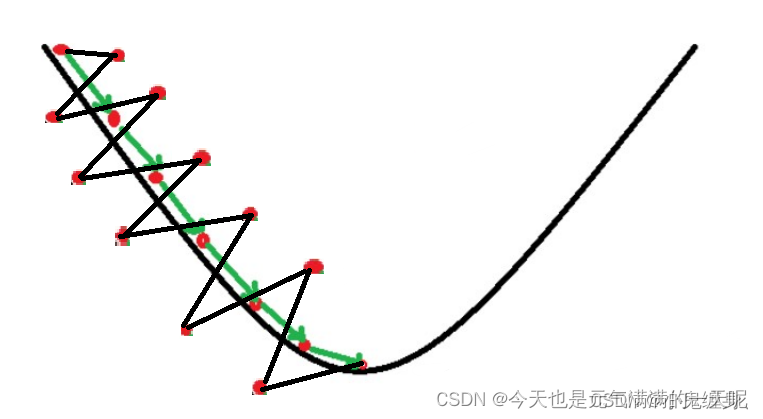
输入x恒大于0,其梯度也不会是最大值,接近0,所以收敛速度变慢。如果对输入进行了0均值化处理,可以使得线性层的值y_mean为0,这样在y'=sigmoid(y),优化w参数时收敛速度快,得到最优w的效率更高,如下图所示,绿线是对x进行零均值后的梯度下降效果,黑线是未进行零均值化的下降效果。【图来自神经网络与深度学习第四章前馈神经网络习题解答-CSDN博客】
习题4-5
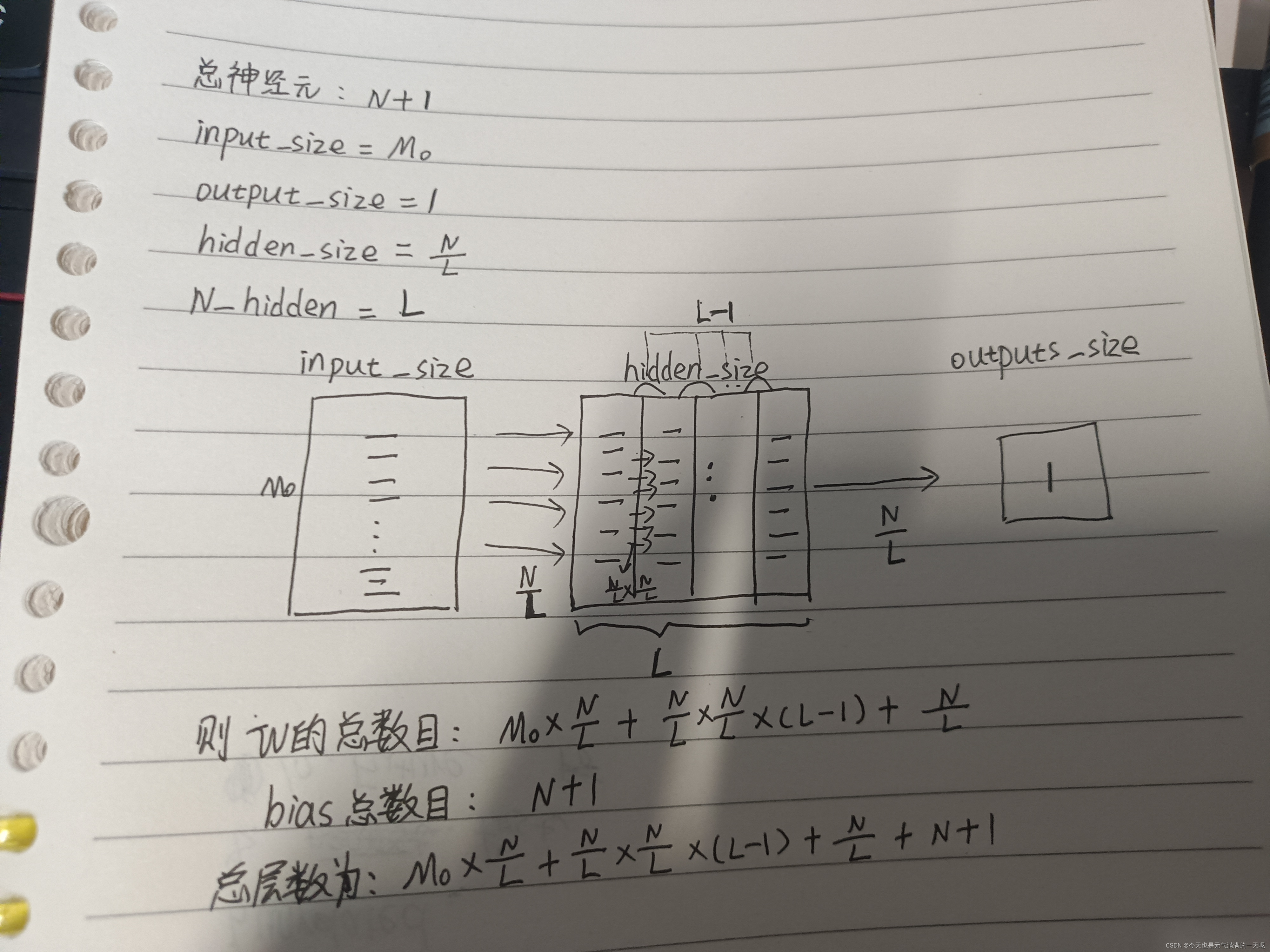
如果限制一个神经网络的总神经元数量(不考虑输入层)为N+1,输入层大小为,输出层大小为1,隐藏层的层数为L,每个隐藏层的神经元数量为
,试分析参数数量和隐藏层层数L的关系.
【最后一行汉字写错了,是总参数数量】
习题4-7
为什么在神经网络模型的结构化风险函数中不对偏置b进行正则化?
正则化目的:为了减少过拟合风险,通过引入正则化惩罚项,可以限制模型参数的大小,可以提高模型的泛化能力。
不对bias正则化的原因:
1.函数y=w*x+bias中bias只影响函数的向上向下平移,它对输入x的变化并不敏感。
2.对bias正则化并不会减少模型的过拟合风险,反而要为它选择合适的正则化系数,使得训练过程更加复杂。
3.对b进行正则化,会减少模型的复杂度,会造成欠拟合情况。
习题4-8
为什么在用反向传播算法进行参数学习时要采用随即参数初始化的方式而不是直接令W=0,b=0?
反向传播算法进行参数学习的过程,就是将最后的误差一层层传入到输入层。
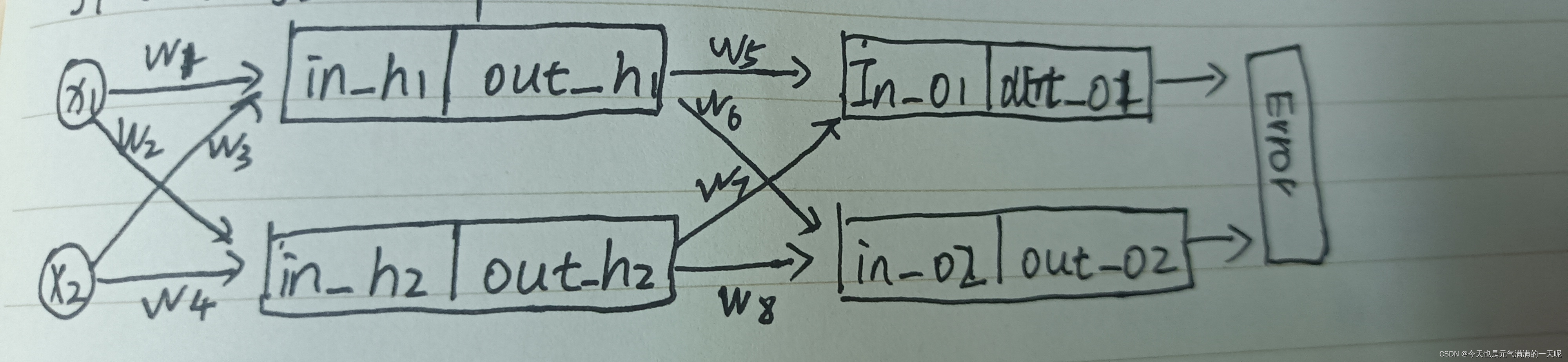
上图可知,在w=0和b=0,前向传播计算得到的隐藏层值都一样,再反向传播中计算得到的梯度一样,那么每层的参数都一样,即相当于中间只有一层隐藏层。多层神经网络就没有意义了。
习题4-9
梯度消失问题是否可以通过增加学习率来缓解
不可以。
梯度消失举个例子,以sigmoid函数为例,在本文的前边的图中可以看到,当值过大过小时,梯度都非常接近于0,更新参数不明显,这就是梯度消失现象。
增加学习率并不会缓解梯度消失,学习率变大时,会使得参数跳过最优值点,然后梯度方向改变,最终导致参数优化时无法收敛。如下图所示【图来自学习率 | 机器之心 (jiqizhixin.com)】。
想要解决梯度下降问题可以使用导数比较大的激活函数,所以可以改成别的激活函数来解决梯度下降问题。【图来自【深度学习】梯度消失和梯度爆炸原因及解决 - 知乎 (zhihu.com)】:
相关文章:

NNDL:作业五
习题4-1 对于一个神经元,并使用梯度下降优化参数w时,如果输入x恒大于0,其收敛速度会比零均值化的输入更慢. 证明: 激活函数以sigmoid为例。 神经元:有两层,线性层和激活层:yw*xb,然后y‘sigmoid(y),也就是。 梯度…...
)
OpenAI大模型项目计划表(InsCode AI 创作助手)
OpenAI大模型项目计划表 阶段任务负责人开始日期完成日期立项确定项目目标和范围项目经理2023-05-012023-05-03确定项目团队和资源项目经理2023-05-042023-05-05确定项目时间表和里程碑项目经理2023-05-062023-05-10数据收集收集训练数据和标注数据团队2023-05-112023-05-20确…...
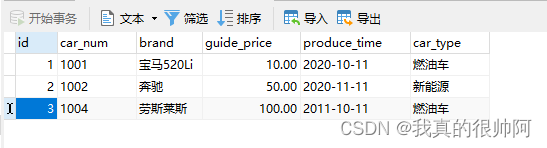
MyBatis入门的第一个程序
2023.10.28 今天正式开始MyBatis的学习,先来一个入门程序的编写。 ①准备一个数据库表: ②配置pom.xml文件:(打包方式和2个依赖的引入) <?xml version"1.0" encoding"UTF-8"?> <proj…...

React项目中使用zustand状态管理详细教程
zustand 是一个用于状态管理的小巧而强大的库,它与 React 非常兼容。以下是使用 zustand 在 React 项目中进行状态管理的详细教程: 步骤 1:安装 zustand 首先,你需要安装 zustand。你可以使用 npm 或 yarn 安装它: …...

Linux 扩展 root 文件系统
本文描述的是通过Linux自带的工具,不用安装额外的包,来实现root文件系统的扩展。 我们可以看到,根盘46.6G: # lsblk NAME MAJ:MIN RM SIZE RO TYPE MOUNTPOINT sda 8:0 0 46.6G 0 disk ├─sda1 …...

19c-rac环境安装AHF
准备给19c rac打补丁,发现tfa报错,如下 [rootdb1 /]# /u01/app/19.0.0/grid_1/OPatch/opatchauto apply /opt/update/35370167/35319490 -oh /u01/app/19.0.0/grid_1 OPatchauto session is initiated at Sat Oct 28 19:33:56 2023 System initializ…...

ESP32网络开发实例-Web控制按钮与硬件状态同步
Web控制按钮与硬件状态同步 文章目录 Web控制按钮与硬件状态同步1、应用介绍2、软件准备3、硬件准备4、代码实现在文中,我们将介绍同时使用网络服务器和物理按钮来控制 ESP32输出。 换句话说,如果用户使用按钮控制 LED,则 LED 的状态也会在 Web 服务器上自动更新。 1、应用介…...
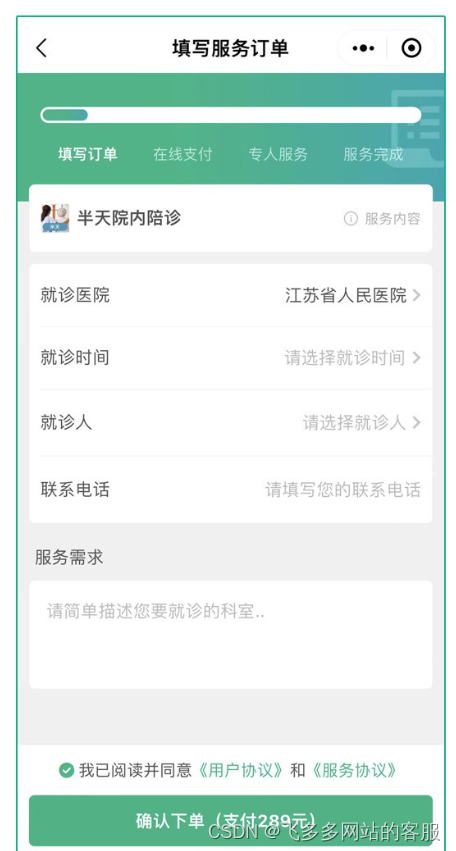
分享一下怎么做陪诊小程序
在当今快节奏的社会中,人们的生活压力越来越大,尤其是在大城市中,由于工作繁忙,生活节奏快,很多人都感到看病难、看病贵的问题。为了解决这一问题,陪诊小程序应运而生。陪诊小程序是一种可以提供线上预约、…...
【Linux】Linux+Nginx部署项目
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于Linux的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.单体项目的部署 0.我们需要将要进行部…...

【git命令】删除分支
1. 删除本地分支 使用git branch -d命令删除本地分支 git branch -d branch_name其中,branch_name是分支名。如果有未合并的更改,Git会阻止你删除分支。 使用git branch -D命令强制删除本地分支 git branch -D branch_name这个命令会强制删除分支&am…...
LabVIEW开发TDS1000 和TDS2000 系列泰克示波器
LabVIEW开发TDS1000 和TDS2000 系列泰克示波器 泰克示波器是经常用到的工具,一般手动操作即可,但有时候也要集成到系统中,需要程控。这时候先要下载厂家提供的例子,了解LabVIEW的demo。根据不用的示波器型号,选择和计…...

1. 两数之和、Leetcode的Python实现
博客主页:🏆看看是李XX还是李歘歘 🏆 🌺每天分享一些包括但不限于计算机基础、算法等相关的知识点🌺 💗点关注不迷路,总有一些📖知识点📖是你想要的💗 ⛽️今…...

TSINGSEE青犀基于AI视频识别技术的平安校园安防视频监控方案
一、背景需求 因学校频频出治安事件,所以必须要加强学校的安防工作,目前来看,大部分校园都建设了视频监控来预防保障校园安全。但是传统的视频监控系统,主要通过设备来录像以及人员时时监控来进行。这种监管方式效率十分低下&…...

基于LSTM encoder-decoder模型实现英文转中文的翻译机器
前言 神经网络机器翻译(NMT, neuro machine tranlation)是AIGC发展道路上的一个重要应用。正是对这个应用的研究,发展出了注意力机制,在此基础上产生了AIGC领域的霸主transformer。我们今天先把注意力机制这些东西放一边,介绍一个对机器翻译…...

世界前沿技术发展报告2023《世界航空技术发展报告》(四)无人机技术
(四)无人机技术 1.无人作战飞机1.1 美国空军披露可与下一代战斗机编组作战的协同式无人作战飞机项目1.2 俄罗斯无人作战飞机取得重要进展 2.支援保障无人机2.1 欧洲无人机项目通过首个里程碑2.2 美国海军继续开展MQ-25无人加油机测试工作 3.微小型无人机…...

【JAVA学习笔记】48 - 八大常用Wrapper类(包装类)
一、包装类 1.针对八种基本定义相应的引用类型一包装类 2.有了类的特点,就可以调用类中的方法。 黄色背景的表示父类是Number 二、包装类和基本数据的转换 演示包装类和基本数据类型的相互转换,这里以int和Integer演示。 1.jdk5前的手动装箱和拆箱方…...

学习笔记:Splay
Splay 定义 Splay 树, 或 伸展树,是一种平衡二叉查找树,它通过 Splay/伸展操作 不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,能够在均摊 O ( log n ) O(\log n) O(logn) 时间内完成插入,查…...
JAVA中的垃圾回收器(1)
一)垃圾回收器概述: 1.1)按照线程数来区分: 串行回收指的是在同一时间端内只允许有一个CPU用于执行垃圾回收操作,此时工作线程被暂停,直至垃圾回收工作结束,在诸如单CPU处理器或者较小的应用内存等硬件平台不是特别优越的场合,出行…...
Windows 10/11如何恢复永久删除的文件?
数据丢失在我们的工作生活中经常发生。当你决定清理硬盘或U盘时,你会删除一些文件夹或文件。如果你通过右键单击删除文件,则可以很容易从回收站恢复已删除的文件。但是,如果你按Shift Delete键、清空回收站或删除大于8998MB的大文件夹&#…...
)
【Shell 系列教程】shell介绍(一)
文章目录 前言Shell 脚本Shell 环境第一个shell脚本运行 Shell 脚本有两种方法:1、作为可执行程序2、作为解释器参数 前言 Shell 是一个用 C 语言编写的程序,它是用户使用 Linux 的桥梁。Shell 既是一种命令语言,又是一种程序设计语言。 Sh…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
