【Codeforces】 CF582D Number of Binominal Coefficients
题目链接
CF方向
Luogu方向
题目解法
看到 p α ∣ ( n k ) p^{\alpha} | \binom{n}{k} pα∣(kn) ,首先想到 k u m m e r kummer kummer 定理,那么限制即为 n − k n-k n−k 和 k k k 做加法在 p p p 进制下的进位数 ≥ α \ge \alpha ≥α
然后就是一个显然的数位 d p dp dp 了
因为进位从前往后数位 d p dp dp 不太好考虑,所以我们考虑从后往前做,然后多记录一维 0 / 1 / 2 0/1/2 0/1/2
我的状态是 f i , j , 0 / 1 , 0 / 1 / 2 f_{i,j,0/1,0/1/2} fi,j,0/1,0/1/2 表示后 i i i 位有 j j j 个进位(不包括第 i i i 位的),这一位是否进位,后面 i i i 位 n n n 与 A A A 的关系(0 表示 n < A n<A n<A,1 表示 n = A n=A n=A,2 表示 n > A n>A n>A)
因为我们把 n , k n,k n,k 变成了 n − k n-k n−k 和 k k k,所以天然保证了 n ≥ k n\ge k n≥k,不需要考虑 n , k n,k n,k 的大小关系
直接 d p dp dp 即可,实现的有些烦,但也不知道可以优化什么了
时间复杂度 O ( n 2 ) O(n^2) O(n2)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=4100,P=1e9+7;
int p,a,f[2][N][2][3];
LL A[N],B[N];
// int g[P];//g[i]表示a+b<=i的方案数(a,b无序)
char str[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
inline void inc(int &x,LL y){ x=(x+y)%P;}
int g(int x){if(x<0) return 0;if(x<p) return (1ll*(x+2)*(x+1)/2)%P;x=p*2-1-x;x=1ll*p*p%P-(1ll*x*(x-1)/2)%P;return x<0?x+P:x;
}
int main(){p=read(),a=read();scanf("%s",str+1);int len=strlen(str+1);for(int i=1;i<=len;i++) A[i]=str[len-i+1]-48;int n=0;for(int i=len;i>=1;i--){for(int j=1;j<N;j++) B[j]*=10;B[1]+=A[i];for(int j=1;j<N;j++) if(B[j]>=p) B[j+1]+=B[j]/p,B[j]%=p;}for(int i=1;i<N;i++) A[i]=B[i];for(int i=1;i<N;i++) if(A[i]) n=i;reverse(A+1,A+n+1);f[(n+1)&1][0][0][1]=1;for(int i=n+1;i>1;i--){int c=A[i-1];int g_c=g(c);int g_c_1=g(c-1);int g_c_2=g(c-2);int g_p_1=g(p-1);int g_p_2=g(p-2);int g_p_c=g(p+c);int g_p_c_1=g(p+c-1);int g_p_c_2=g(p+c-2);int g_2p_2=g(p*2-2);int g_2p_3=g(p*2-3);memset(f[~i&1],0,sizeof(f[~i&1]));for(int j=0;j<=n-i+1;j++){//calc f[~i&1][j][0][0]inc(f[~i&1][j][0][0],1ll*f[i&1][j][0][0]*g_c);if(c){for(int t:{1,2}) inc(f[~i&1][j][0][0],1ll*f[i&1][j][0][t]*g_c_1);if(j){inc(f[~i&1][j][0][0],1ll*f[i&1][j-1][1][0]*g_c_1);if(c>1) for(int t:{1,2}) inc(f[~i&1][j][0][0],1ll*f[i&1][j-1][1][t]*g_c_2);}}//calc f[~i&1][j][0][1]if(!c) inc(f[~i&1][j][0][1],1ll*f[i&1][j][0][1]*g_c);else inc(f[~i&1][j][0][1],1ll*f[i&1][j][0][1]*(g_c-g_c_1+P));if(j&&c) inc(f[~i&1][j][0][1],1ll*f[i&1][j-1][1][1]*(g_c_1-g_c_2+P));//calc f[~i&1][j][0][2]for(int t:{0,1}) inc(f[~i&1][j][0][2],1ll*f[i&1][j][0][t]*(g_p_1-g_c+P));inc(f[~i&1][j][0][2],1ll*f[i&1][j][0][2]*(g_p_1-g_c_1+P));if(j){for(int t:{0,1}) inc(f[~i&1][j][0][2],1ll*f[i&1][j-1][1][t]*(g_p_2-g_c_1+P));inc(f[~i&1][j][0][2],1ll*f[i&1][j-1][1][2]*(g_p_2-g_c_2+P));}//calc f[~i&1][j][1][0]inc(f[~i&1][j][1][0],1ll*f[i&1][j][0][0]*(g_p_c-g_p_1+P));for(int t:{1,2}) inc(f[~i&1][j][1][0],1ll*f[i&1][j][0][t]*(g_p_c_1-g_p_1+P));if(j){inc(f[~i&1][j][1][0],1ll*f[i&1][j-1][1][0]*(g_p_c_1-g_p_2+P));for(int t:{1,2}) inc(f[~i&1][j][1][0],1ll*f[i&1][j-1][1][t]*(g_p_c_2-g_p_2+P));}//calc f[~i&1][j][1][1]inc(f[~i&1][j][1][1],1ll*f[i&1][j][0][1]*(g_p_c-g_p_c_1+P));if(j) inc(f[~i&1][j][1][1],1ll*f[i&1][j-1][1][1]*(g_p_c_1-g_p_c_2+P));//calc f[~i&1][j][1][2]for(int t:{0,1}) inc(f[~i&1][j][1][2],1ll*f[i&1][j][0][t]*(g_2p_2-g_p_c+P));inc(f[~i&1][j][1][2],1ll*f[i&1][j][0][2]*(g_2p_2-g_p_c_1+P));if(j){for(int t:{0,1}) inc(f[~i&1][j][1][2],1ll*f[i&1][j-1][1][t]*(g_2p_2-g_p_c_1+P));inc(f[~i&1][j][1][2],1ll*f[i&1][j-1][1][2]*(g_2p_2-g_p_c_2+P));}}}int ans=0;for(int i=a;i<=n;i++) inc(ans,1ll*f[1][i][0][0]+f[1][i][0][1]);printf("%d\n",ans);fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}
/*
f[i][j][0/1][0/1/2]:到第i位,后j位已经填好且进位了j次,这一位是否进位,n后面j位和A的关系(0小于,1等于,2大于)
*/相关文章:

【Codeforces】 CF582D Number of Binominal Coefficients
题目链接 CF方向 Luogu方向 题目解法 看到 p α ∣ ( n k ) p^{\alpha} | \binom{n}{k} pα∣(kn) ,首先想到 k u m m e r kummer kummer 定理,那么限制即为 n − k n-k n−k 和 k k k 做加法在 p p p 进制下的进位数 ≥ α \ge \alpha ≥α …...
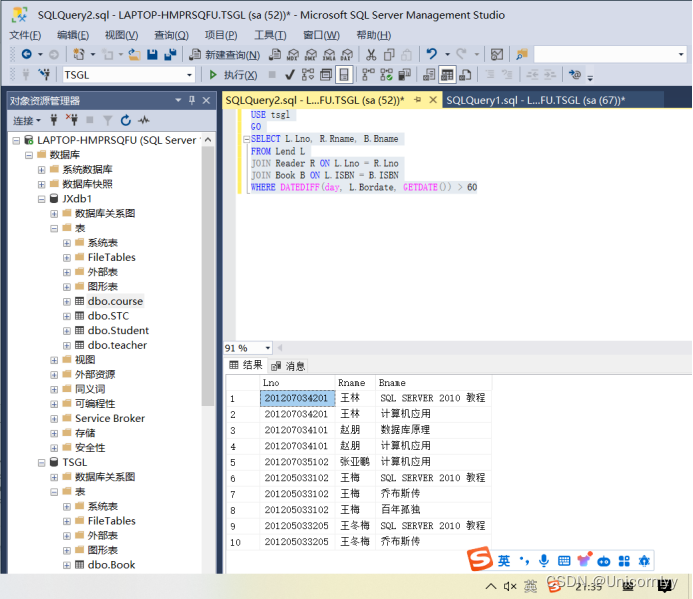
sql第二次上机作业
1查找借阅了ISBN为“4-6045-1023-4”的借书证号,读者姓名,专业名和借书时间 use tsgl go select Reader.Lno,Rname,Spec,Lend.Bordate FROM Reader,Lend WHERE Reader.LnoLend.Lno AND ISBN 4-6045-1023-42查找借阅了《数据库原理》一书的借阅信息&…...
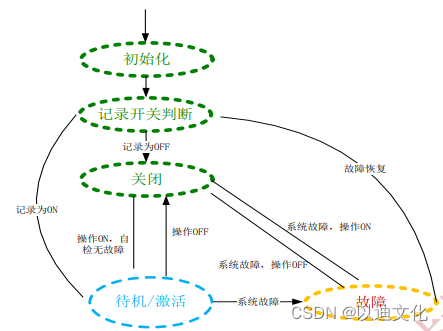
辅助驾驶功能开发-功能规范篇(22)-3-L2级辅助驾驶方案功能规范
1.3.3 TLA系统功能定义 1.3.3.1 状态机 1.3.3.2 状态迁移图 1.3.3.3 功能定义 1.3.3.3.1 信号需求列表 1.3.3.3.2 系统开启关闭 1)初始化 车辆上电后,交通灯辅助系统(TLA)进行初始化,控制器需在 220ms 内发出第一帧报文,并在 3s 内完成内部自检,同时上电 3s 内不进行…...
)
Python基础入门例程16-NP16 发送offer(列表)
目录 描述 输入描述: 输出描述: 解答 : 说明: 描述 某公司在面试结束后,创建了一个依次包含字符串 Allen 和 Tom 的列表offer_list,作为通过面试的名单。 请你依次对列表中的名字发送类似 Allen, you…...

Web前端面试之Vue—对Vue的理解
目录 一、web发展历程 二、vue是什么 三、Vue核心特性 组件化 数据驱动 指令 四、Vue与Angular以及React的区别 一、web发展历程 Web是World Wide Web的简称,中文译为万维网 我们可以将它规划成如下的几个时代来进行理解 静态网页:最早的网页是没…...

C/C++晶晶赴约会 2020年12月电子学会青少年软件编程(C/C++)等级考试一级真题答案解析
目录 C/C晶晶赴约会 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序编写 四、程序说明 五、运行结果 六、考点分析 C/C晶晶赴约会 2020年12月 C/C编程等级考试一级编程题 一、题目要求 1、编程实现 晶晶的朋友贝贝约晶晶下周一起去看展览࿰…...

js 解决 H 指数
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。 根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 是指他(她)至少发…...

在JS中,var 、let 、const 总结
let是英文单词"let"的缩写。在JavaScript中,let 关键字用来声明一个块级作用域 的变量,这意味着变量仅在声明它的代码块内有效,超出该代码块作用域时就无法访问该变量。与var不同的是,let不会被提升到函数作用域或全局作…...
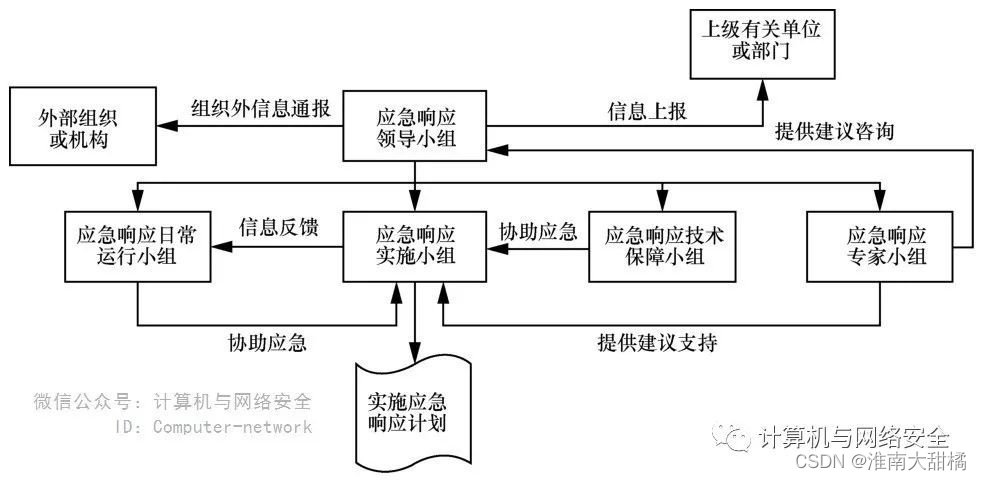
关于网络安全运营工作与安全建设工作的一些思考
以下内容是个人成长过程中对于网络安全运营工作的理解和思考,希望通过这篇文章帮助大家更好的去做安全运营体系化建设,开始吧! 文章目录 一、网络安全运营是什么?二、网络安全运营建设阶段第一阶段:设备限制阶段第二阶…...

【机器学习可解释性】4.SHAP 值
机器学习可解释性 1.模型洞察的价值2.特征重要性排列3.部分依赖图4.SHAP 值5.SHAP 值 高级使用 正文 理解各自特征的预测结果? 介绍 您已经看到(并使用)了从机器学习模型中提取一般解释技术。但是,如果你想要打破模型对单个预测的工作原理? SHAP 值…...

OpenCV官方教程中文版 —— 直方图均衡化
OpenCV官方教程中文版 —— 直方图均衡化 前言一、原理二、 OpenCV 中的直方图均衡化三、 CLAHE 有限对比适应性直方图均衡化 前言 本小节我们要学习直方图均衡化的概念,以及如何使用它来改善图片的对比。 一、原理 想象一下如果一副图像中的大多是像素点的像素值…...
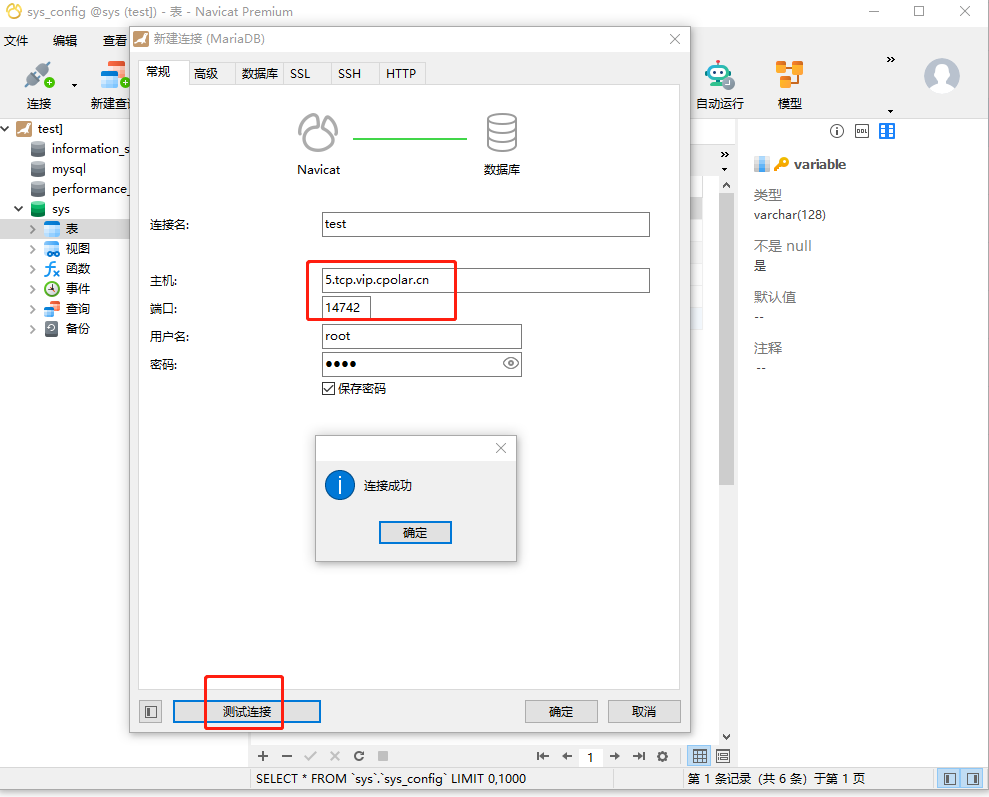
如何使用navicat图形化工具远程连接MariaDB数据库【cpolar内网穿透】
公网远程连接MariaDB数据库【cpolar内网穿透】 文章目录 公网远程连接MariaDB数据库【cpolar内网穿透】1. 配置MariaDB数据库1.1 安装MariaDB数据库1.2 测试局域网内远程连接 2. 内网穿透2.1 创建隧道映射2.2 测试随机地址公网远程访问3. 配置固定TCP端口地址3.1 保留一个固定的…...

【uniapp】uview1.x使用upload上传图片
和2.x不同的是,要用 action 来配置后端上传图片的接口地址; 再来一些配置项的命名有所不同,一般1.x的命名用 -,2.x的命名使用小驼峰; 1.x 的上传会自带删除时的提示框,2.x 没有; 重要的几个配置…...
基于nodejs+vue食力派网上订餐系统
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

软件测试常用的8种功能测试类型有哪些?
软件测试常用的8种功能测试类型有哪些? 单元测试 单元测试确保在一个段中编写的每一段代码都能产生最佳结果。开发人员在单元测试期间只看接口和确定部件。它提供了代码进展的文档,因为每个代码单元在继续下一个之前都经过了彻底的测试。 集成测试 至少对…...

动态规划之01背包问题
01背包问题 1. 【模板】01背包2. 分割等和子集3. 目标和4. 最后一块石头的重量 II 01背包问题是一种动态规划问题,用于求解在有限容量的背包中装入最大价值的物品组合。具体步骤如下: 定义一个二维数组dp[i][j],表示从前i个物品中选择若干个…...
安防监控项目---boa服务器的移植
文章目录 前言一、boa服务器简介二、移植步骤三、测试结果四、A9平台移植BOA总结 前言 书接上期,在配置完成环境后,那么接下来呢还得移植两个非常关键的东西,一个呢时boa服务器,另一个呢时cgi接口,boa服务器能够使得我…...

Gson 字符串常用转换方式(集合转换为Json数组
数组转换为 Json 字符串: GsonUtils.toJson(itemListBean.getImgs())json 字符串转换为数组 Gson().fromJson(goodsDbBean.getImgs(), String[].class)Json 转换为已知实体类 GsonUtils.parseJSON(result, AFileInfoBean.class);Json 转换为已知实体类集合 List<…...
)
MyBatis的使用(XML映射文件)
MyBatis的使用(XML映射文件) MyBatis基于注解开发简单便捷,但是弊端是失去SQL语句的灵活性,不能根据实际情况产生不同的SQL语句 MyBatis除了支持注解开发以外,还支持一种开发方式:XML映射文件,…...
localhost知识
文章目录 一、localhost是什么?二、localhost 在平时用到的地方三、 localhost 与 127.0.01 一、localhost是什么? localhost 是一个特殊的主机名,通常指代本机。它被用来进行本地开发和测试,也常被用作网络配置中的占位符&#…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...

分布式光纤声振传感技术原理与瑞利散射机制解析
分布式光纤传感技术(Distributed Fiber Optic Sensing,简称DFOS)作为近年来迅速发展的新型感知手段,已广泛应用于边界安防、油气管道监测、结构健康诊断、地震探测等领域。其子类技术——分布式光纤声振传感(Distribut…...

2025年上海市“星光计划”第十一届职业院校技能大赛 网络安全赛项技能操作模块样题
2025年上海市“星光计划”第十一届职业院校技能大赛 网络安全赛项技能操作模块样题 (二)模块 A:安全事件响应、网络安全数据取证、应用安全、系统安全任务一:漏洞扫描与利用:任务二:Windows 操作系统渗透测试 :任务三&…...
