如何使用 nvm-windows 这个工具来管理你电脑上的Node.js版本

nvm-windows 是一个用于管理在 Windows 上安装的多个 Node.js 版本的工具。以下是安装和使用 nvm-windows 的步骤:
第1步:下载 nvm-windows
- 访问
nvm-windows的 GitHub发布页面. - 下载最新版本的
nvm-setup.zip文件。
第2步:安装 nvm-windows
- 解压
nvm-setup.zip文件。 - 打开解压后的文件夹,双击
nvm-setup.exe文件以运行安装程序。 - 跟随安装程序的指引完成安装。
第3步:安装 Node.js
- 打开命令提示符(Cmd)或 PowerShell。
- 输入以下命令来安装 Node.js 的特定版本(例如,16.0.0):
nvm install 16.0.0 - 安装完成后,设置刚刚安装的 Node.js 版本为当前使用的版本:
nvm use 16.0.0
第4步:验证安装
- 输入以下命令来确认
nvm已经成功安装并且正在使用正确的 Node.js 版本:nvm list node --version
nvm list 应该会显示已安装的 Node.js 版本列表,node --version 应该会显示当前使用的 Node.js 版本,确保这个版本是你刚刚安装并设置的版本。
nvm install 16.0.0 安装慢如何加速?
nvm install 下载和安装 Node.js 版本时可能会比较慢,这主要取决于你的网络连接速度以及你下载内容的源服务器的速度。以下是一些可能帮助你加速安装过程的建议:
1. 使用国内镜像
如果你在中国,由于网络原因,直接从国外服务器下载 Node.js 可能会非常慢。你可以尝试使用国内的镜像来加速下载。nvm-windows 允许你指定 Node.js 的下载镜像。例如,你可以使用淘宝的 Node.js 镜像:
nvm node_mirror https://npm.taobao.org/mirrors/node/
nvm npm_mirror https://npm.taobao.org/mirrors/npm/
设置完镜像后,再次尝试安装 Node.js 版本:
nvm install 16.0.0
2. 确保你的网络连接稳定
有时网络不稳定也会导致下载变慢。确保你的网络连接是稳定的,并尝试重新启动你的路由器或调整网络设置。
3. 尝试其他版本或其他时间
可能是因为特定版本的 Node.js 在服务器上没有准备好,或者在你尝试下载的时候服务器负载较重。你可以尝试安装其他版本的 Node.js,或者在其他时间再次尝试安装。
4. 手动下载并安装
你可以直接从 Node.js 的官方网站或者使用国内镜像手动下载 Node.js 的二进制文件,然后使用 nvm 的 install 命令来从本地安装。
例如,下载了 Node.js v16.0.0 的 Windows 64位二进制文件到 C:\path\to\node-v16.0.0-win-x64.zip,你可以使用以下命令进行安装:
nvm install 16.0.0 64 C:\path\to\node-v16.0.0-win-x64.zip
这些方法中的一些或全部可能会帮助你加速 nvm install 的过程。
相关文章:

如何使用 nvm-windows 这个工具来管理你电脑上的Node.js版本
nvm-windows 是一个用于管理在 Windows 上安装的多个 Node.js 版本的工具。以下是安装和使用 nvm-windows 的步骤: 第1步:下载 nvm-windows 访问 nvm-windows 的 GitHub发布页面.下载最新版本的 nvm-setup.zip 文件。 第2步:安装 nvm-wind…...
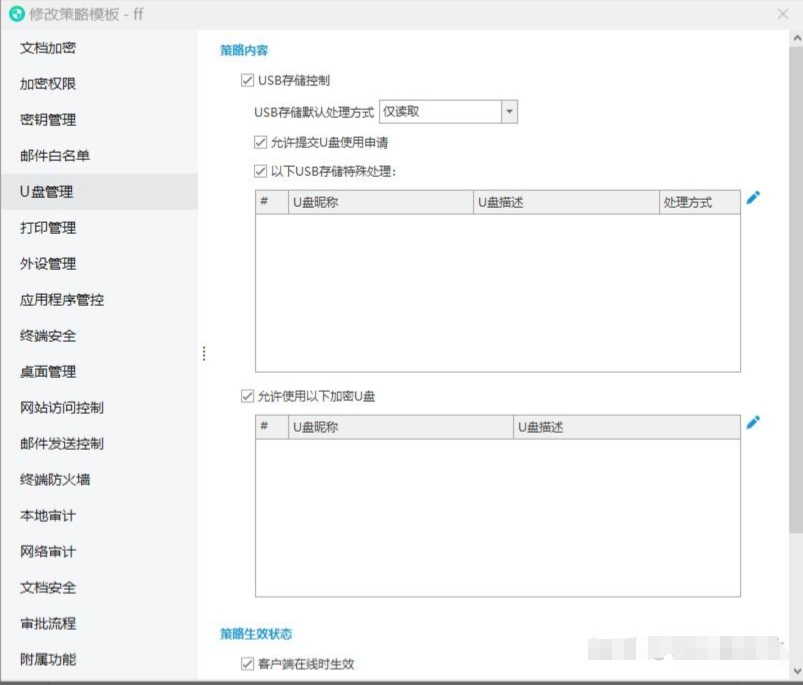
公司电脑禁用U盘的方法
公司电脑禁用U盘的方法 安企神U盘管理系统下载使用 在这个复杂的数据时代,保护公司数据的安全性至关重要。其中,防止未经授权的数据泄露是其中的一个关键环节。U盘作为一种常用的数据传输工具,也成为了潜在的安全风险。因此,公司…...

Elasticsearch 7.X版本常用语法语句
文章目录 监控相关 API查看健康状况查看所有节点查看所有节点详细信息查看主节点查看所有索引查看所有分片 索引管理创建索引查看索引查看索引字段类型修改索引字段删除索引别名给索引添加别名查询某个索引下的别名给索引更换别名给索引解绑别名一个别名绑定多个索引查询index_…...
)
Python分享之数学与随机数 (math包,random包)
我们在Python运算中看到Python最基本的数学运算功能。此外,math包补充了更多的函数。当然,如果想要更加高级的数学功能,可以考虑选择标准库之外的numpy和scipy项目,它们不但支持数组和矩阵运算,还有丰富的数学和物理方…...
Linux 基本语句_8_C语言_文件控制
为了解决多个进程同时操作一个文件,产生一些情况,通常对文件进行上锁,已解决对共享文件的竞争 对打开文件进行各种操作: int fcentl(int fd, int cmd, .../*arg*/如果cmd与锁操作有关,那么fcentl函数的第三个参数就要…...

博通BCM575系列 RDMA 网卡驱动 bnxt_re 分析(一)
简介 整个BCM系列驱动分成以太网部分(bnxt_en.ko)和RDMA部分(bnxt_re.ko), 两个模块之间通过内核的auxiliary_bus进行管理.我们主要分析下bnxt_re驱动. 代码结构 这个驱动的核心是 qplib_fp.c, 这个文件主要包含了驱动的数据路径, 包括Post Send, Post Recv, Poll CQ流程的实…...
ExcelPatternTool 开箱即用的Excel工具包现已发布!
文章目录 ExcelPatternTool功能特点:快速开始使用说明常规类型高级类型Importable注解Exportable注解IImportOption导入选项IExportOption导出选项单元格样式StyleMapping样式映射使用数据库作为数据源 示例Sample1:不同类型字段导出Sample2:…...
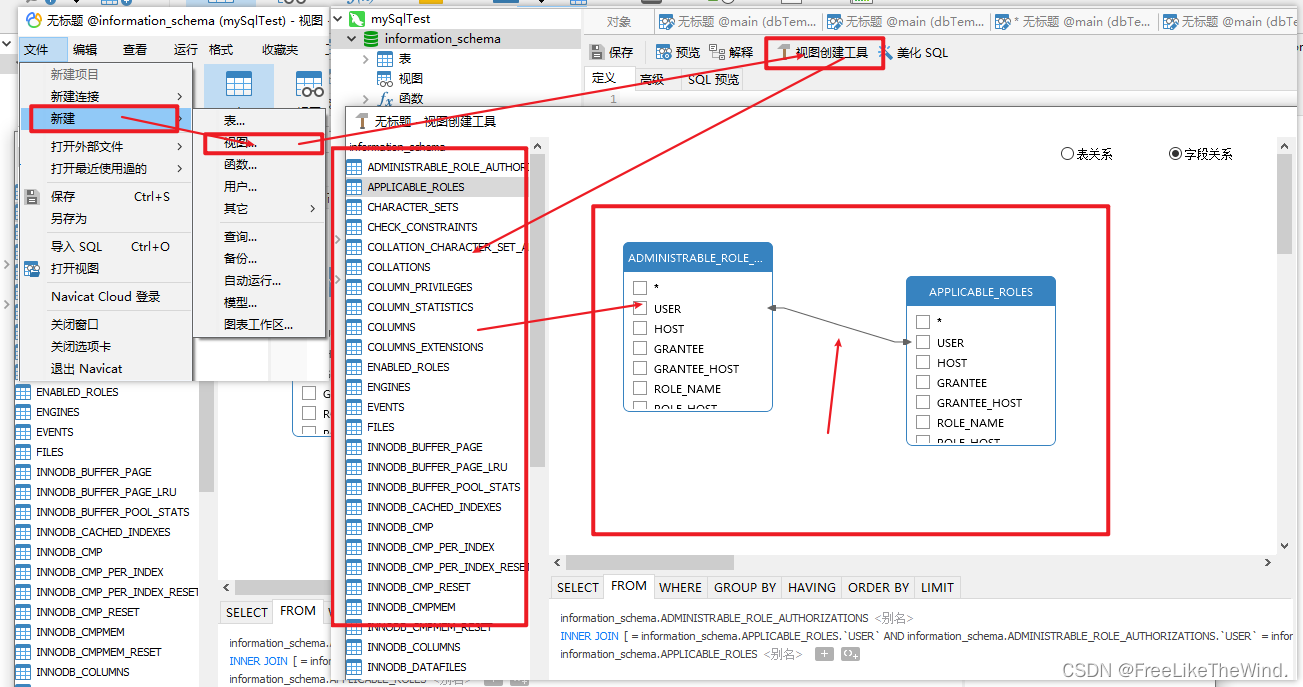
Navicat for MySQL 视图创建使用方法
创建视图步骤: 点击新建;选择视图;点击视图创建工具;可以在左侧拖拽表到工作区;选择表字段进行连线...

计算机视觉的相机选型
#你一般什么时候会用到GPT?# 目前市面上的工业相机大多是基于CCD(ChargeCoupled Device)或CMOS(Complementary Metal Oxide Semiconductor)芯片的相机。一般CCD制造工艺更加复杂,也会更贵一点! 1、CCD工…...
实体店做商城小程序如何
互联网电商深入各个行业,传统线下店商家无论产品销售还是服务业,仅靠以往的经营模式,很难拓展到客户,老客流失严重,同时渠道单一,无法实现外地客户购物及线上客户赋能等。 入驻第三方平台有优势但也有不足…...
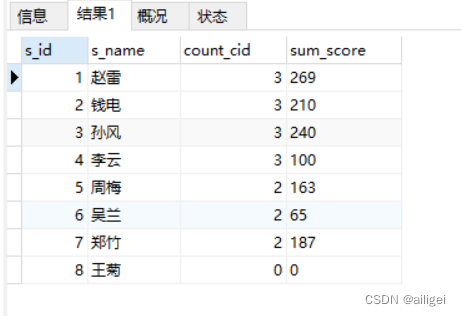
sql-50练习题0-5
sql练习题0-5题 前言数据库表结构介绍学生表课程表成绩表教师表 0-1 查询"01"课程比"02"课程成绩高的学生的信息及课程分数0-2查询"01"课程比"02"课程成绩小的学生的信息及课程分数0-3查询平均成绩大于等于60分的同学的学生编号和学生…...

Flutter框架实现登录注册功能,不连接数据库
要在Flutter框架中实现登录和注册功能,而不连接数据库,可以使用本地存储来存储用户信息。以下是一个简单的示例,演示如何使用本地存储来实现登录和注册功能。 首先,我们需要添加 shared_preferences 插件到 pubspec.yaml 文件中&…...

持续集成部署-k8s-部署利器-Helm
这里写目录标题 1. Helm 是什么?2. 快速安装 Helm2.1 前置条件2.2 Helm 版本与 K8s 版本对应关系2.3 离线安装 Helm3. Helm 常用命令1. Helm 是什么? Helm 是一个用于 Kubernetes 应用程序部署和管理的开源工具。它可以帮助简化 Kubernetes 应用程序的打包、发布、配置和升级…...

替换所有的问号
这篇也是凑数的 哈哈.... 稍后会整合到算法通关第三关白银挑战 . 描述 : 给你一个仅包含小写英文字母和 ? 字符的字符串 s,请你将所有的 ? 转换为若干小写字母,使最终的字符串不包含任何 连续重复 的字符。 注意 : 不能 修改非 ? 字符 . 题目 : …...
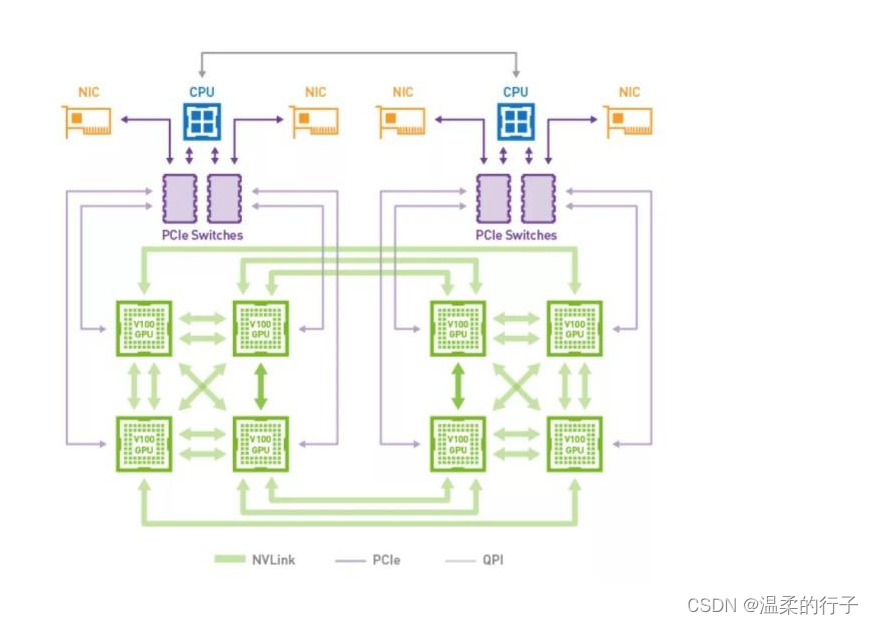
NCCL后端
"NCCL" 代表 "NVIDIA Collective Communications Library","NVIDIA 集体通信库",它是一种由 NVIDIA 开发的用于高性能计算的通信库。NCCL 专门设计用于加速 GPU 群集之间的通信,以便在并行计算和深度学习等领域…...
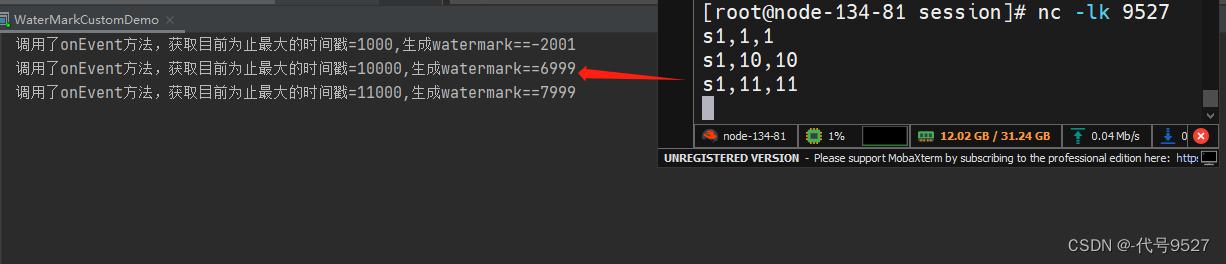
【API篇】十、生成Flink水位线
文章目录 1、水位线的生成原则2、有序流内置水位线3、乱序流内置水位线4、自定义周期性水位线生成器5、自定义断点式水位线生成器6、从数据源中发送水位线 1、水位线的生成原则 水位线出现,即代表这个时间之前的数据已经全部到齐,之后不会再出现之前的数…...
【Javascript】弹出框
目录 警告框 确认框 提示框 警告框 alert(你好); 确认框 var isConfirm confirm(请确认) console.log( isConfirm); 提示框...
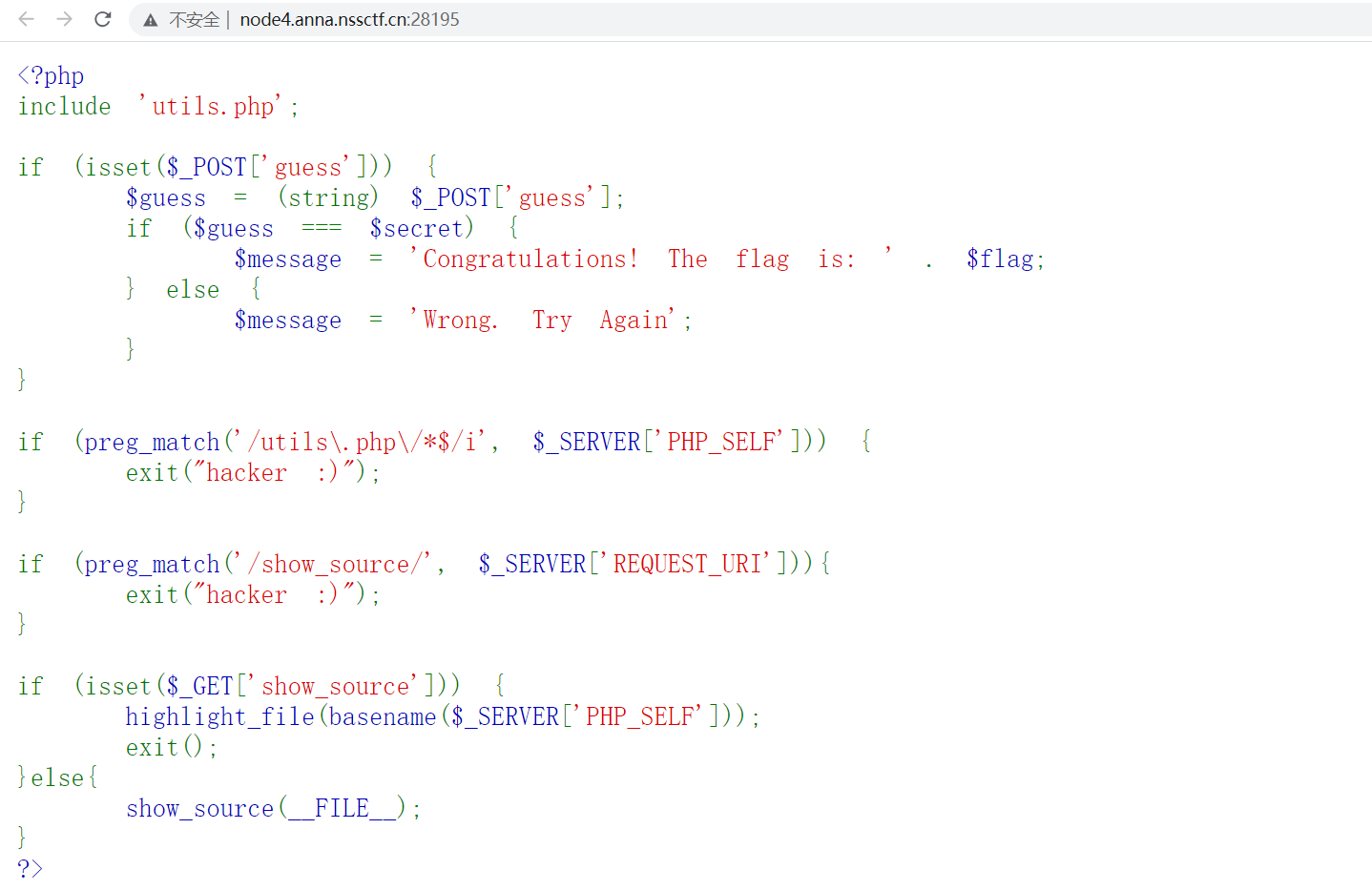
NSS [鹤城杯 2021]EasyP
NSS [鹤城杯 2021]EasyP 直接给了源码 <?php include utils.php;if (isset($_POST[guess])) {$guess (string) $_POST[guess];if ($guess $secret) {$message Congratulations! The flag is: . $flag;} else {$message Wrong. Try Again;} }if (preg_match(/utils\.p…...
)
mysql用户及权限管理(InsCode AI 创作助手)
MySQL是一个广泛使用的开源关系型数据库管理系统,用于存储和管理大量数据。对于那些需要使用MySQL的管理员和开发人员来说,用户权限管理是确保数据库安全性的至关重要的一环。在本篇技术博客中,我们将深入探讨MySQL的用户权限管理,…...
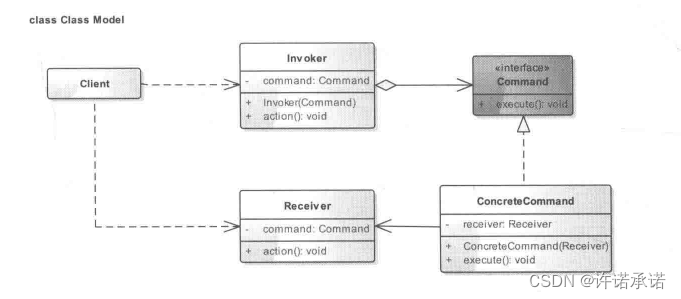
命令模式——让程序舒畅执行
● 命令模式介绍 命令模式(Command Pattern),是行为型设计模式之一。命令模式相对于其他的设计模式来说并没有那么多条条框框,其实并不是一个很“规矩”的模式,不过,就是基于一点,命令模式相对于…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
