搜索与图论:匈牙利算法
将所有点分成两个集合,使得所有边只出现在集合之间,就是二分图
二分图:一定不含有奇数个点数的环;可能包含长度为偶数的环, 不一定是连通图
二分图的最大匹配:
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510 , M = 100010;
int n1,n2,m;
int h[N],ne[M],e[M],idx;//邻接表
bool st[N];
int match[N];void add(int a , int b)
{//头插法//如图 如1与2之间要有一条线,让2的ne为1,再让h[1]为2的索引。//这样h[1]就是1节点存的最后一个相连的点,如图就是7节点。//而在索引表内部,通过头插法的方式(即每次ne指向上一个点(h存的就是上一个点)),索引表为:7->4->2e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}int find(int x)
{//遍历自己喜欢的女孩for(int i = h[x] ; i != -1 ;i = ne[i]){int j = e[i];if(!st[j])//如果在这一轮模拟匹配中,这个女孩尚未被预定{st[j] = true;//那x就预定这个女孩了,这里预定是防止她男朋友找其他喜欢的女孩时不重复找这个//如果女孩j没有男朋友,或者她原来的男朋友能够预定其它喜欢的女孩。配对成功if(!match[j]||find(match[j])){match[j] = x;return true;}}}//自己中意的全部都被预定了。配对失败。return false;
}int main()
{memset(h,-1,sizeof h);scanf("%d%d%d",&n1,&n2,&m);while(m--){int a,b;scanf("%d%d",&a,&b);add(a,b);}int res = 0;for(int i = 1; i <= n1 ;i ++){ //因为每次模拟匹配的预定情况都是不一样的所以每轮模拟都要初始化memset(st,false,sizeof st);if(find(i)) res++;//找到一条边,则res++} printf("%d\n",res);
}
相关文章:

搜索与图论:匈牙利算法
将所有点分成两个集合,使得所有边只出现在集合之间,就是二分图 二分图:一定不含有奇数个点数的环;可能包含长度为偶数的环, 不一定是连通图 二分图的最大匹配: #include<iostream> #include<cs…...

明星艺人类的百度百科怎么创建 ?
明星艺人们的知名度对于其事业的成功至关重要,而作为国内最大的中文百科全书网站,百度百科成为了人们获取信息的重要来源。一线明星当然百科不用自己操心,平台和网友就给维护了,但是刚刚走红的明星艺人应提早布局百科词条…...

类EMD的“信号分解方法”及MATLAB实现(第八篇)——离散小波变换DWT(小波分解)
在之前的系列文章里,我们介绍了EEMD、CEEMD、CEEMDAN、VMD、ICEEMDAN、LMD、EWT,我们继续补完该系列。 今天要讲到的是小波分解,通常也就是指离散小波变换(Discrete Wavelet Transform, DWT)。在网上有一些介绍该方法…...
python随手小练10(南农作业题)
题目1: 编写程序,输出1~1000之间所有能被4整除,但是不能被5整除的数 具体操作: for i in range(1,1000): #循环遍历1~999,因为range是左闭右开if (i % 4 0) and (i % 5 ! 0) :print(i) 结果展示: 题目2&…...

How to install mongodb-7.0 as systemd service with podman
How to install mongodb-7.0 as systemd service with podman 1、安装1.1、创建卷1.2、配置文件1.3、创建容器1.4、服务管理1.5、容器管理 2、客户端管理 1、安装 1.1、创建卷 配置卷 podman volume create --label typemongo-7.0 --label envdev mongo-7.0-conf数据卷 pod…...

一文彻底理解python浅拷贝和深拷贝
目录 一、必备知识二、基本概念三、列表,元组,集合,字符串,字典浅拷贝3.1 列表3.2 元组3.3 集合3.4 字符串3.5 字典3.6 特别注意浅拷贝总结 四、列表,元组,集合,字符串,字典深拷贝 一…...

什么是软件的生命周期?全方位解释软件的生命周期
软件的生命周期 软件生命周期是指从软件产品的设想开始到软件不再使用而结束的时间。 如果把软件看成是有生命的事 物,那么软件的生命周期可以分成6个阶段,即需求分析、计划、设计、编码、测试、运行维护 需求分析阶段: 分析需求的可行性&…...

网络安全—小白自学
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟…...

List 3.5 详解原码、反码、补码
前言 欢迎来到我的博客,我是雨空集(全网同名),无论你是无意中发现我,还是有意搜索而来,我都感到荣幸。这里是一个分享知识、交流想法的平台,我希望我的博客能给你带来帮助和启发。如果你喜欢我…...

数据清洗与规范化详解
数据处理流程,也称数据处理管道,是将原始数据转化为有意义的信息和知识的一系列操作步骤。它包括数据采集、清洗、转换、分析和可视化等环节,旨在提供有用的见解和决策支持。在数据可视化中数据处理是可视化展示前非常重要的一步,…...

Ansible playbook的block
环境 控制节点:Ubuntu 22.04Ansible 2.10.8管理节点:CentOS 8 block 顾名思义,通过block可以把task按逻辑划分到不同的“块”里面,实现“块操作”。此外,block还提供了错误处理功能。 task分组 下面的例子&#x…...

Jupyter Notebook还有魔术命令?太好使了
在Jupyter Notebooks中,Magic commands(以下简称魔术命令)是一组便捷的功能,旨在解决数据分析中的一些常见问题,可以使用%lsmagic 命令查看所有可用的魔术命令 插播,更多文字总结指南实用工具科技前沿动态…...

DailyRecord-231029
iOS&前端: 数组 iOS/Xcode异常:对象数组NSMutableArray添加元素-addObject,但count方法仍然返回0? - 周文 - 博客园(需要初始化) [__NSArrayI addObject:]: unrecognized selector sent to instance (检查addObj…...

雨云虚拟主机使用教程WordPress博客网站搭建教程
雨云虚拟主机(RVH)使用教程与宝塔面板搭建WordPress博客网站的教程,本文会讲解用宝塔面板一键部署以及手动安装两种方式来搭建WordPress博客,选其中一种方式即可。 WordPress WordPress是使用PHP语言开发的博客平台,用户可以在支持PHP和MyS…...

【SPSS】基于RFM+Kmeans聚类的客户分群分析(文末送书)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
回溯法(1)--装载问题和0-1背包
一、回溯法 回溯法采用DFS+剪枝的方式,通过剪枝删掉不满足条件的树,提高本身作为穷举搜索的效率。 回溯法一般有子集树和排列树两种方式,下面的装载问题和01背包问题属于子集树的范畴。 解空间类型: 子集树࿱…...
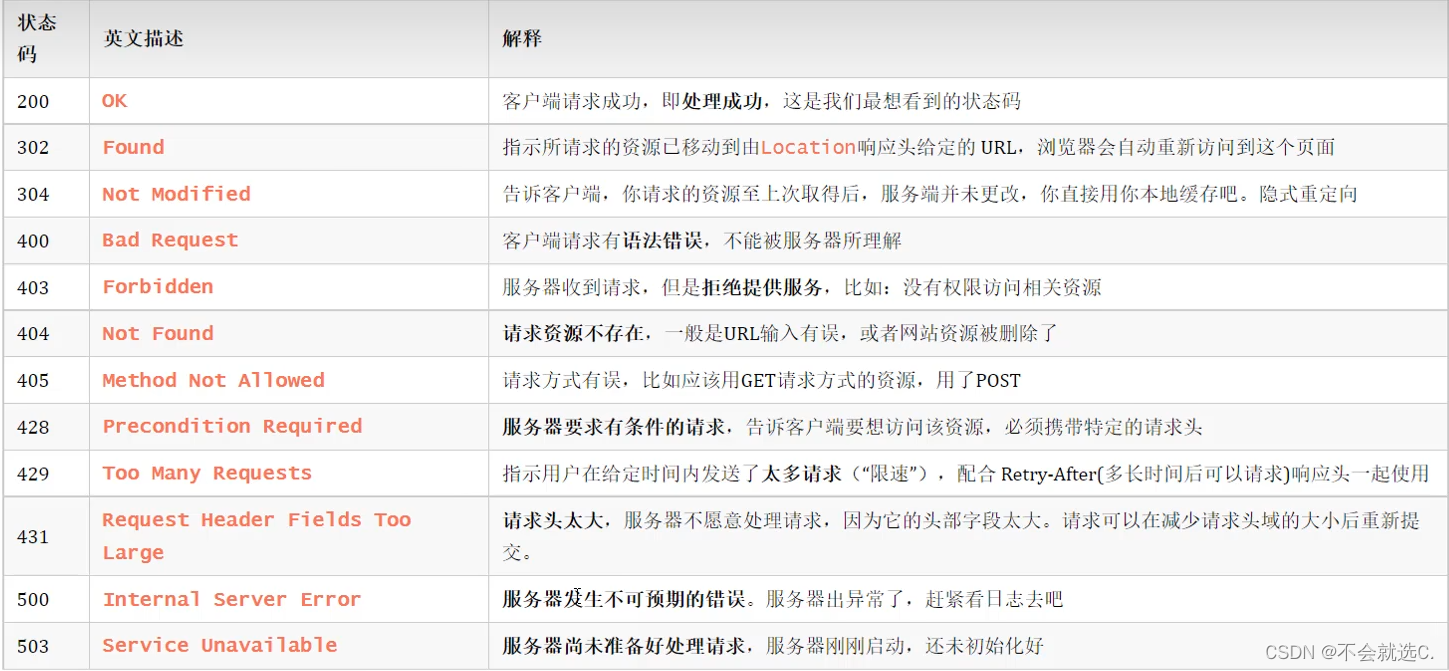
[javaweb]——HTTP请求与响应协议,常见响应状态码(如:404)
🌈键盘敲烂,年薪30万🌈 目录 HTTP概述 📕概念:Hyper Text Transfer Protocol,超文本传输协议,规定了浏览器和服务器之间数据传输的规则。 📕特点: 📕插播…...

Java面向对象(进阶)-- 拼电商客户管理系统(康师傅)
文章目录 一、目标二、需求说明(1)主菜单(2)添加客户(3)修改客户(4)删除客户(5)客户列表 三、软件设计结构四、类的设计(1)Customer类…...

Qt配置OpenCV教程,亲测已试过
详细版可参考:Qt配置OpenCV教程,亲测已试过(详细版)_qt opencv_-_Matrix_-的博客-CSDN博客 软件准备:QtOpenCVCMake (QtOpenCV安装不说了,CMake的安装,我用的是:可参考博客&#x…...

【实用网站分享】
1、PyDebloatX https://pydebloatx.com/pydebloatx 是一种用于 Windows 操作系统的 Python 脚本,用于卸载 Windows 10 系统中的预装应用和系统组件,以便提高系统性能和释放磁盘空间。它是 Debloat Windows 10 脚本的一个分支,但具有更友好和…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
