LeetCode 104. 二叉树的最大深度
LeetCode 104. 二叉树的最大深度
难度:easy\color{Green}{easy}easy
题目描述
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7][3,9,20,null,null,15,7][3,9,20,null,null,15,7],
3/ \9 20/ \15 7
返回它的最大深度 3 。
算法
(递归)
递归求解:
当前树的最大深度等于左右子树的最大深度加1。
复杂度分析
-
时间复杂度:树中每个节点只被遍历一次,所以时间复杂度是O(n)O(n)O(n)。
-
空间复杂度 : O(1)O(1)O(1)
C++ 代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int maxDepth(TreeNode* root) {if (!root) return 0;return max(maxDepth(root->left), maxDepth(root->right)) + 1;}
};
相关文章:

LeetCode 104. 二叉树的最大深度
LeetCode 104. 二叉树的最大深度 难度:easy\color{Green}{easy}easy 题目描述 给定一个二叉树,找出其最大深度。 二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。 说明: 叶子节点是指没有子节点的节点。 示例: 给定二叉树 [3…...

pandas 中如何按行或列的值对数据排序?
在处理表格型数据时,常会用到排序,比如,按某一行或列的值对表格排序,要怎么做呢? 这就要用到 pandas 中的 sort_values() 函数。 一、 按列的值对数据排序 先来看最常见的情况。 1.按某一列的值对数据排序 以下面…...

「牛客网C」初学者入门训练BC139,BC158
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练 🔥座右铭:“不要等到什么都没有了,才下定决心去做” 🚀🚀🚀大家觉不错…...
【深度学习】线性回归、逻辑回归、二分类,多分类等基础知识总结
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言1. 线性回归2、逻辑回归3. 单层神经元的缺陷&多层感知机softmax 多分类最后再来一个 二分类的例子前言 入行深度学习快2年了,是时间好好总结下基础知识了.现…...

【MySQL】调控 字符集
一、 MySQL 启动选项 & 系统变量 启动选项 是在程序启动时我们程序员传递的一些参数,而 系统变量 是影响服务器程序运行行为的变量 1.1 启动项 MySQL 客户端设置项包括: 允许连入的客户端数量 、 客户端与服务器的通信方式 、 表的默认存储引擎 、…...
FME+YOLOV7写DNF自动刷图脚本
目录 前言 一、难点分析 二、实现流程 1.DNF窗口位置获取 2.获取训练数据 3.数据标注 4.数据格式转换 5.数据训练 5.刷图逻辑编写 前言 这是一篇不务正业的研究,首先说明,这不是外挂!这不是外挂!这不是外挂!这只是用a…...

Java语法面试题
多线程锁 Synchronized:一次只能被一个线程占有ReadWriteLock:被多个线程持有,写锁只能被一个线程占有ReentrantLock:一个线程的多个流程能获取同一把锁,就是可重入锁,即在一个线程中可以被重复的获取自旋锁…...

location
目录 匹配的目标 格式 匹配符号: 优先级 要表达不匹配条件,则用 if 实现 例子:根目录的匹配最弱 例子:区分大小写 和 不区分大小写 例子:以根开头 和 不区分大小写 例子:等号 匹配的目标 ng…...

简述RBAC模型
RBAC(Role-Based Access Control)模型是一种常用的访问控制模型,用于管理和控制用户对系统资源的访问权限。RBAC模型通过将用户分配给角色,并授予角色相应的权限,来实现安全的资源访问管理。 在RBAC模型中,…...

倒计时2天:中国工程院院士谭建荣等嘉宾确认出席,“警务+”时代来临...
近日伴随公安部、科技部联合印发通知,部署推进科技兴警三年行动计划(2023-2025年),现代科技手段与警务工作相结合的方式,正式被定义为未来警务发展的新趋势。 21世纪以来,随着科技的不断发展和创新…...
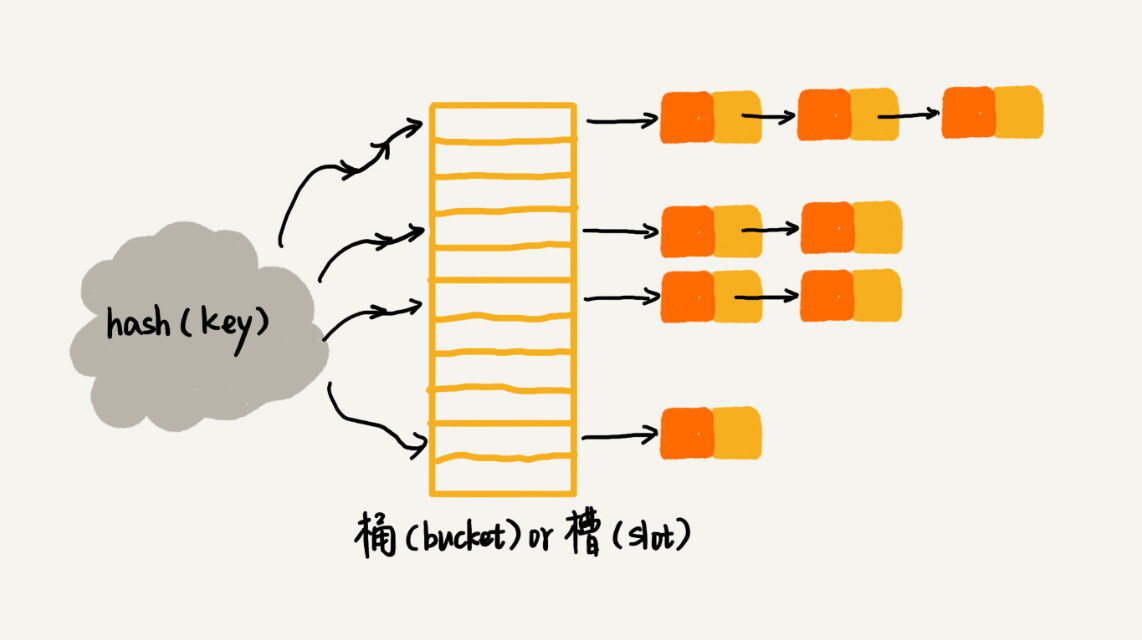
Python蓝桥杯训练:基本数据结构 [哈希表]
Python蓝桥杯训练:基本数据结构 [哈希表] 文章目录Python蓝桥杯训练:基本数据结构 [哈希表]一、哈希表理论基础知识1、开放寻址法2、链式法二、有关哈希表的一些常见操作三、力扣上面一些有关哈希表的题目练习1、[有效的字母异位词](https://leetcode.cn…...

MacOS 配置 Fvm环境
系统环境:MacOS 13,M1芯片 1. 安装HomeBrew: /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)" speed 2. 使用brew安装Fvm: brew tap leoafarias/fvm brew install fvm 3…...
 介绍 Python 编程语言)
Python小白入门- 01( 第一章,第1节) 介绍 Python 编程语言
1. 介绍 Python 编程语言 1.1 Python 是什么 Python 是一种高级的、解释型、面向对象的编程语言,具有简洁、易读、易写的语法特点。Python 由 Guido van Rossum 于 1989 年在荷兰创造,并于 1991 年正式发布。 Python 语言广泛应用于数据科学、Web 开发、人工智能、自动化测…...

高并发系统设计之缓存
本文已收录至Github,推荐阅读 👉 Java随想录 这篇文章来讲讲缓存。缓存是优化网站性能的第一手段,目的是让访问速度更快。 说起缓存,第一反应可能想到的就是Redis。目前比较好的方案是使用多级缓存,如CPU→Ll/L2/L3→…...

【N32WB03x SDK使用指南】
【N32WB03x SDK使用指南】1. 简介1.1 产品简介1.2 主要资源1.3 典型应用2. SDK/开发固件文件目录结构2.1 doc2.2 firmware2.3 middleware2.4 utilities2.5 projects Projects3. 项目配置与烧录3.1 编译环境安装3.2 固件支持包安装3.3 编译环境配置3.4 编译与下载3.5 BLE工程目录…...

pytest测试框架——pytest.ini用法
这里写目录标题一、pytest用法总结二、pytest.ini是什么三、改变运行规则pytest.inicheck_demo.py执行测试用例四、添加默认参数五、指定执行目录六、日志配置七、pytest插件分类八、pytest常用插件九、改变测试用例的执行顺序十、pytest并行与分布式执行十一、pytest内置插件h…...
2023版)
KAFKA安装与配置(带Zookeeper)2023版
KAFKA安装与配置(带Zookeeper) 一、环境准备: Ubuntu 64位 22.04,三台 二、安装JDK1.8 下载JDK1.8,我这边用的版本是jdk1.8.0_2022、解压jdk tar -zxvf jdk1.8.0_202.tar.gz 3、在/usr/local创建java文件夹,并将解压的jdk移动到/usr/local/java sudo mv jdk1.8.0_202…...

深入浅出解析ChatGPT引领的科技浪潮【AI行研商业价值分析】
Rocky Ding写在前面 【AI行研&商业价值分析】栏目专注于分享AI行业中最新热点/风口的思考与判断。也欢迎大家提出宝贵的意见或优化ideas,一起交流学习💪 大家好,我是Rocky。 2022年底,ChatGPT横空出世,火爆全网&a…...

.net 批量导出文件,以ZIP压缩方式导出
1. 首先Nuget ICSharpCode.SharpZipLib <script type"text/javascript">$(function () {$("#OutPutLink").click(function () { // 单击下文件时$.ajax({ // 先判断条件时间内没有文件url: "/Home/ExistsFile?statTime" $(&q…...
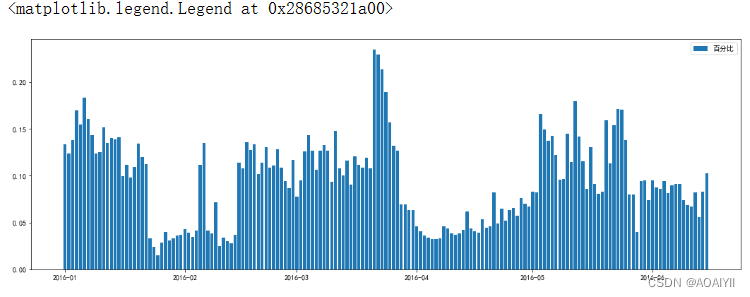
数据分析:某电商优惠卷数据分析
数据分析:某电商优惠卷数据分析 作者:AOAIYI 专栏:python数据分析 作者简介:Python领域新星作者、多项比赛获奖者:AOAIYI首页 😊😊😊如果觉得文章不错或能帮助到你学习,可…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
