算法篇 : 并查集
介绍
英文名:union find set
作用:合并集合,查询集合
合并:将有直接关系的顶点放在一个集合里面
查找:查询某个顶点所属的集合
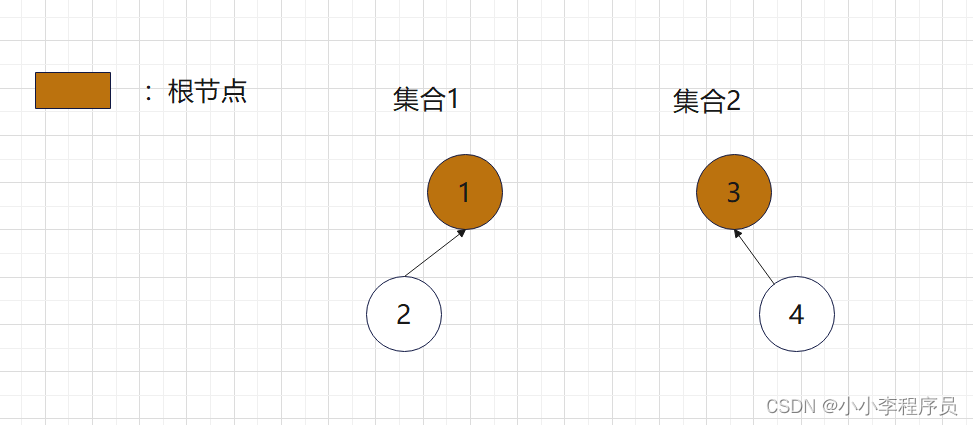
集合的标志:用祖先点的标号作为每个集合的标识
案例
如果说将下图的集合2合并至集合1
那么应该让3的祖先为1,即:
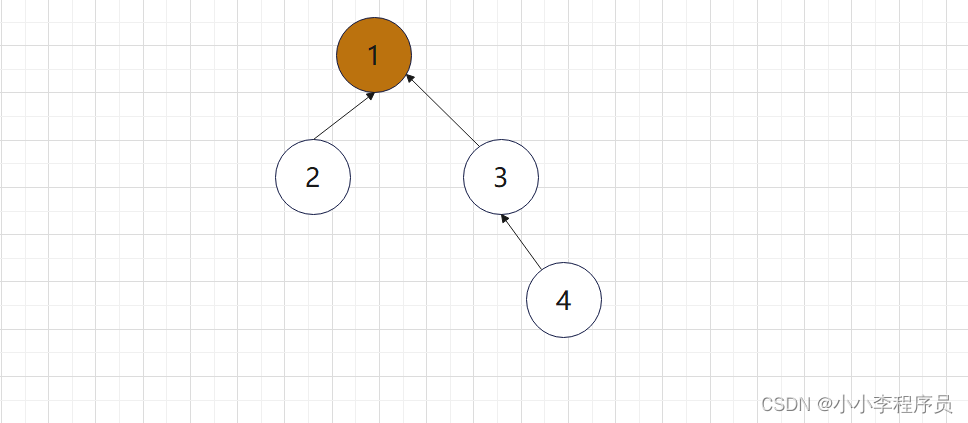
实现流程
1)对所有顶点标号,其祖先节点默认为自己
2)合并:以两个点中祖先标号小的作为新祖先进行合并
3)查找:查找点的祖先,并更新查找路径点的祖先
Java代码实现
//顶点类
public class Vertex {public Integer id;public Vertex(Integer id){this.id=id;}
}//并查集的操作类
public class UnionFindSetOperator {private List<Vertex>vertexs; //所有顶点private List<List<Vertex>>connectVertexs; //所有有直接关系的顶点private Map<Vertex,Vertex>ancestor;public UnionFindSetOperator(List<Vertex> vertexs, List<List<Vertex>> connectVertexs) {this.vertexs = vertexs;this.connectVertexs = connectVertexs;this.ancestor=new HashMap<>();//将所有顶点的祖先初始化默认设置为自己for(int i=0;i< vertexs.size();i++){ancestor.put(vertexs.get(i),vertexs.get(i));}//合并所有直接相连的顶点for(int i=0;i< connectVertexs.size();i++){Union(connectVertexs.get(i).get(0),connectVertexs.get(i).get(1));}}public void Union(Vertex vertex1,Vertex vertex2){Vertex ancestor1=Find(vertex1);Vertex ancestor2=Find(vertex2);//选取两个祖先id小的作为新祖先if(ancestor1.id<ancestor2.id)ancestor.put(vertex2,ancestor1);elseancestor.put(vertex1,ancestor2);}public Vertex Find(Vertex vertex){if(ancestor.get(vertex)!=vertex){//寻找该节点的祖先Vertex ancestorVertex=Find(ancestor.get(vertex));//如果祖先发生了变化,则更新记录新的祖先if(ancestorVertex!=ancestor.get(vertex))ancestor.put(vertex,ancestorVertex);}//返回其祖先return ancestor.get(vertex);}
}
测试函数
//测试函数
public class Main {/*并查集:简述:对集合进行分类合并,方便后续查找实现步骤:1)对所有顶点标号,其祖先节点默认为自己2)合并:以两个点中祖先标号小的作为新祖先进行合并3)查找:查找点的祖先,并更新查找路径点的祖先*/public static void main(String[] args) {//扫描器Scanner scanner=new Scanner(System.in);//存放顶点List<Vertex>vertexs=new LinkedList<>();//有直接关联的顶点List<List<Vertex>>connectVertexs=new LinkedList<>();System.out.println("请输入顶点的数量:");Integer vexcnt= scanner.nextInt();System.out.println("请输入这些顶点的编号");for(int i=0;i<vexcnt;i++){vertexs.add(new Vertex(scanner.nextInt()));}System.out.println("请输入有关系顶点的对数:");Integer connectVertexCnt= scanner.nextInt();System.out.println("请输入有关系顶点的编号:");for(int i=0;i<connectVertexCnt;i++){Integer id1= scanner.nextInt();Integer id2= scanner.nextInt();//获取这两个顶点Vertex v1=null;Vertex v2=null;for(int j=0;j<vertexs.size();j++){if(vertexs.get(j).id==id1)v1=vertexs.get(j);if(vertexs.get(j).id==id2)v2=vertexs.get(j);}LinkedList<Vertex>conVertexs=new LinkedList<>();conVertexs.add(v1);conVertexs.add(v2);connectVertexs.add(conVertexs);}//用并查集的操作类实现这些点的分类和查找UnionFindSetOperator ufs=new UnionFindSetOperator(vertexs,connectVertexs);//查找每一个点的祖先for(int i=0;i<vertexs.size();i++){Vertex ancestor=ufs.Find(vertexs.get(i));System.out.println("顶点:"+vertexs.get(i).id+"的祖先id为:"+ancestor.id);}}
}
自测
测试模型:
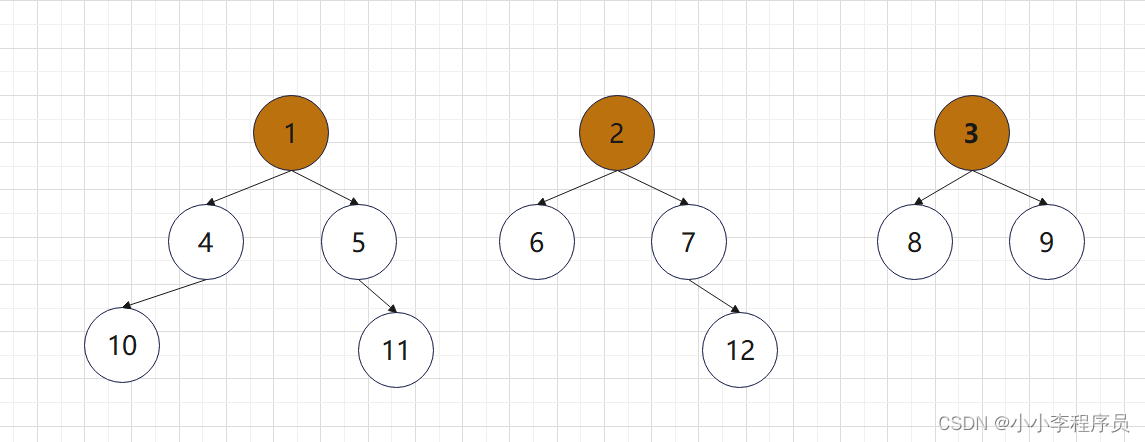
测试结果:

相关文章:

算法篇 : 并查集
介绍 英文名:union find set 作用:合并集合,查询集合 合并:将有直接关系的顶点放在一个集合里面 查找:查询某个顶点所属的集合 集合的标志:用祖先点的标号作为每个集合的标识 案例 如果说将下图的集合2合并…...

AM@微积分基本定理@微积分第二基本定理
文章目录 abstract微积分第二基本定理微积分基本公式公式书写例 结合不定积分的方法求定积分定积分换元法证明 定积分换元公式逆用例 和不定积分第二类换元法的差别定积分分部积分法例 abstract 微积分第一基本定理告诉我们,总是能够通过积分法构造(表达)一个连续函数的原函数…...

goland常用快捷键
移动光标 控制光标的移动:fn上下左右 移至当前页的页头:ctrlPgUp 移至并选中光标到当前页头:ctrlshiftPgUp 移至当前页的页尾:ctrlPgDn 移至并选中当前光标到当前页尾:ctrlshiftPgDn 返回到当前的光标处…...

CSDN写文章时常见问题及技巧
CSDN写文章时常见问题及技巧 1.有序待续、更新中 1.有序 过程: 写 1.空格 ,注意“.”后加个空格就可以生成序号,随心所欲编辑了 待续、更新中 ————————————————————— 以上就是今日博客的全部内容了 创作不易,若对您有…...
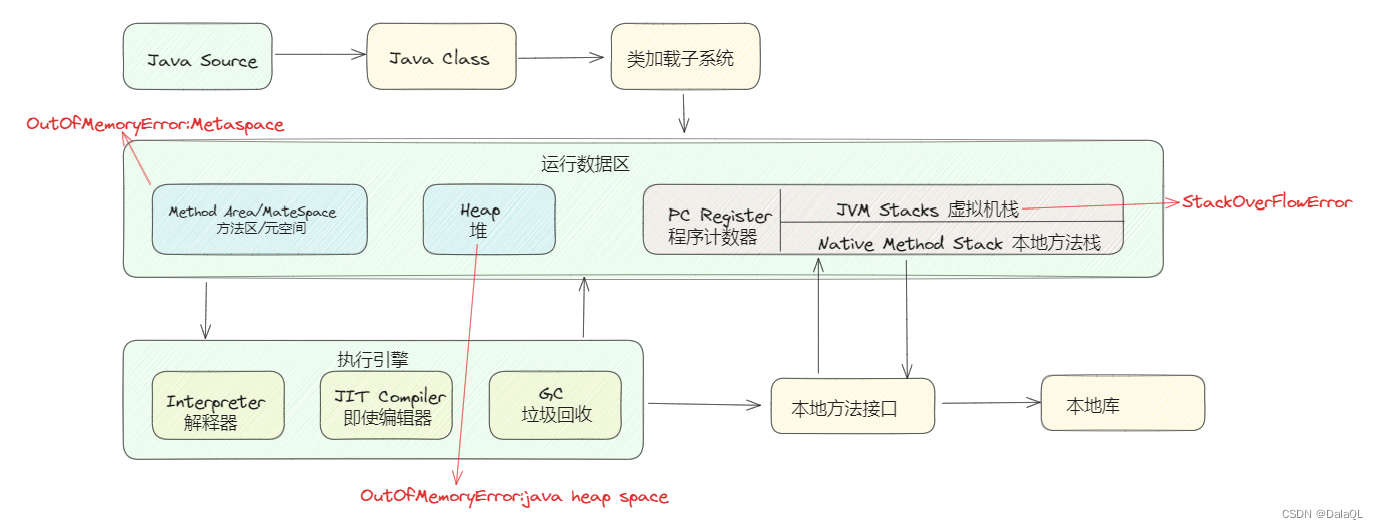
JVM虚拟机详解
目录 01JVM由哪些部分组成/运行流程 什么是程序计数器 详细介绍堆 介绍方法区(Method Area) 直接内存 虚拟机栈(Java Virtual machine Stacks) 垃圾回收是否涉及栈内存 栈内存分配越大越好吗 方法内的局部变量是否线程安全 什么情况下会导致栈…...

Go 怎么操作 OSS 阿里云对象存储
1 介绍 在项目开发中,我们经常会使用对象存储,比如 Amazon 的 S3,腾讯云的 COS,阿里云的 OSS 等。本文我们以阿里云 OSS 为例,介绍怎么使用 Go 操作对象存储。 阿里云 OSS 提供了 REST Api 和 OSS Go SDK࿰…...

vue3 Suspense组件
在 Vue 3 中,<Suspense> 组件用于处理异步组件加载时的等待状态和错误处理。它允许你在加载异步组件时显示一个自定义的加载指示器,以及在加载失败时显示错误信息。以下是一个详细的 <Suspense> 组件的使用示例: 首先࿰…...

NlogPrismWPF
文章目录 Nlog&Prism&WPF日志模块实现原理添加配置注入服务应用测试其他模块怎么调用? Nlog&Prism&WPF 日志模块 介绍了为WPF框架Prism注册Nlog日志服务的方法 实现原理 无论是在WPF或者ASP.NET Core当中, 都可以使用ServiceCollection来做到着…...
, 文件上传实战绕过思路, 基础篇)
文件上传漏洞(2), 文件上传实战绕过思路, 基础篇
文件上传漏洞实战思路(基础) 准备一句话木马文件 mm.php 一, 前端绕过 p1 浏览器禁用js先把mm.php后缀名修改为mm.jpg, 点击提交后, 用 burp 截取请求, 将数据包中的文件名修改回mm.php再提交. 二, 类型MIME绕过 p2 使用 burp 修改 Content-Type: image/jpeg 三, 黑名单绕…...
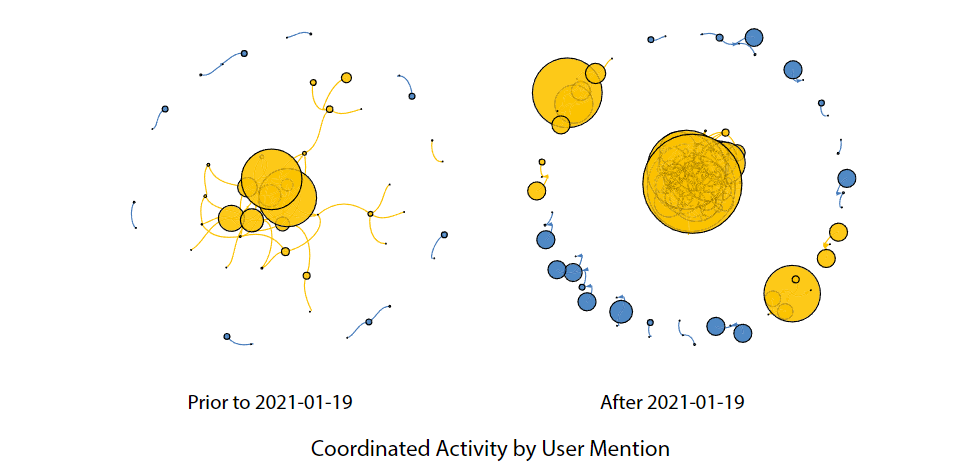
论文阅读 - Hidden messages: mapping nations’ media campaigns
论文链接: https://link.springer.com/content/pdf/10.1007/s10588-023-09382-7.pdf 目录 1 Introduction 2 The influence model 2.1 The influence‑model library 3 Data 4 Methodology 4.1 Constructing observations 4.2 Learning the state‑transiti…...

[AutoSAR系列] 1.3 AutoSar 架构
依AutoSAR及经验辛苦整理,原创保护,禁止转载。 专栏 《深入浅出AutoSAR》 1. 整体架构 图片来源: AutoSar 官网 从官往图中可以看出autosar作为汽车ECU软件架构,是通过分层来实现软硬件隔离。就像大多数操作系统一样ÿ…...
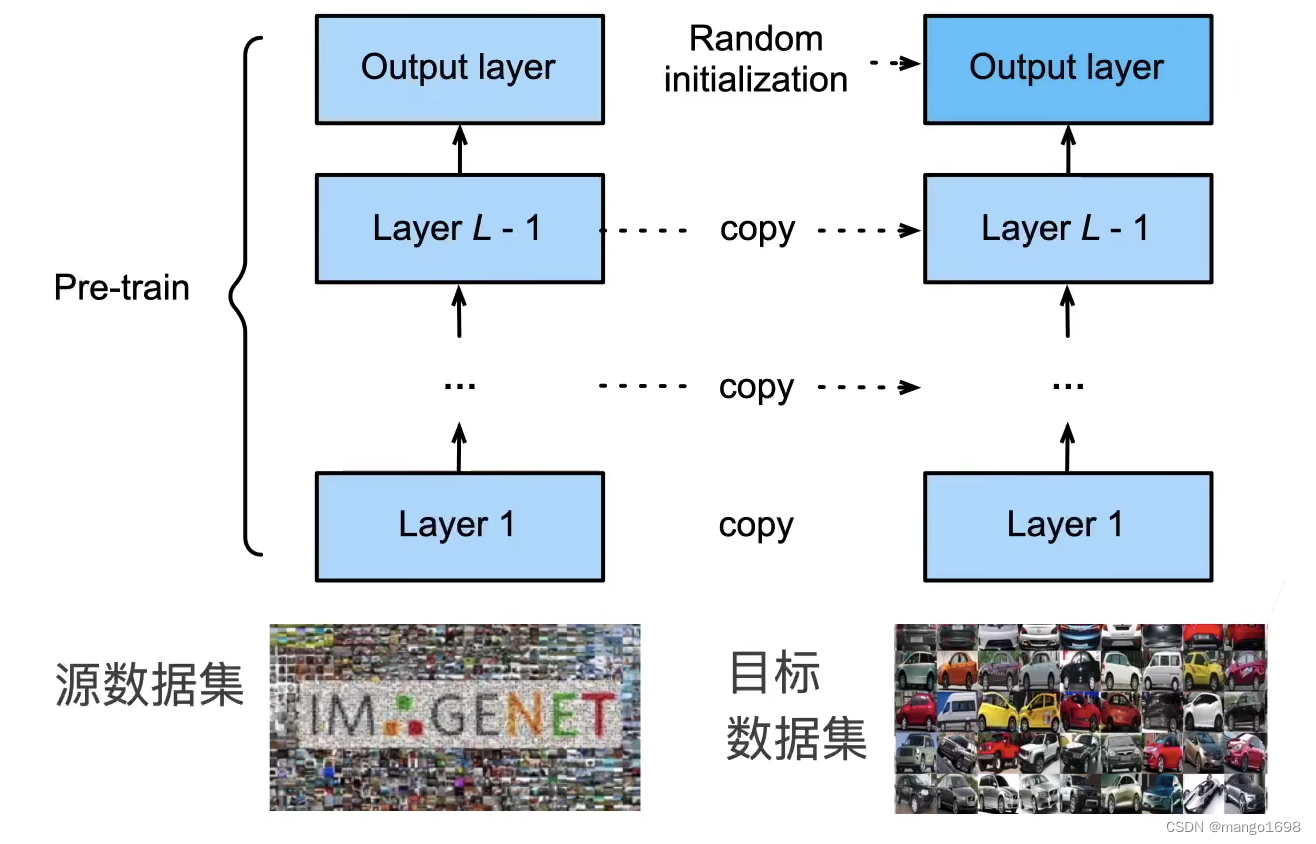
迁移学习 - 微调
什么是与训练和微调? 你需要搭建一个网络模型来完成一个特定的图像分类的任务。首先,你需要随机初始化参数,然后开始训练网络,不断调整参数,直到网络的损失越来越小。在训练的过程中,一开始初始化的参数会…...

09 用户态跟踪:如何使用eBPF排查应用程序?
09 用户态跟踪:如何使用eBPF排查应用程序? sudo bpftrace -e usdt:/usr/bin/python3:function__entry { printf("%s:%d %s\n", str(arg0), arg2, str(arg1))} # -*- coding: UTF-8 -*- import socket from socket import SOL_SOCKET, SO_R…...
深入浅出排序算法之堆排序
目录 1. 算法介绍 2. 执行流程⭐⭐⭐⭐⭐✔ 3. 代码实现 4. 性能分析 1. 算法介绍 堆是一种数据结构,可以把堆看成一棵完全二叉树,这棵完全二叉树满足:任何一个非叶结点的值都不大于(或不小于)其左右孩子结点的值。若父亲大孩子小&#x…...
—— tcpdump)
Linux 命令(11)—— tcpdump
文章目录 一、命令简介二、使用方法三、命令选项四、基本语法和使用方法1. 显示 ASCII 字符串2. 抓取特定协议的数据3. 抓取特定主机的数据4. 将抓取的数据写入文件5. 行缓冲模式 五、理解tcpdump的输出六、过滤表达式1. Host 过滤2. Network 过滤3. Proto 过滤4. Port 过滤5. …...
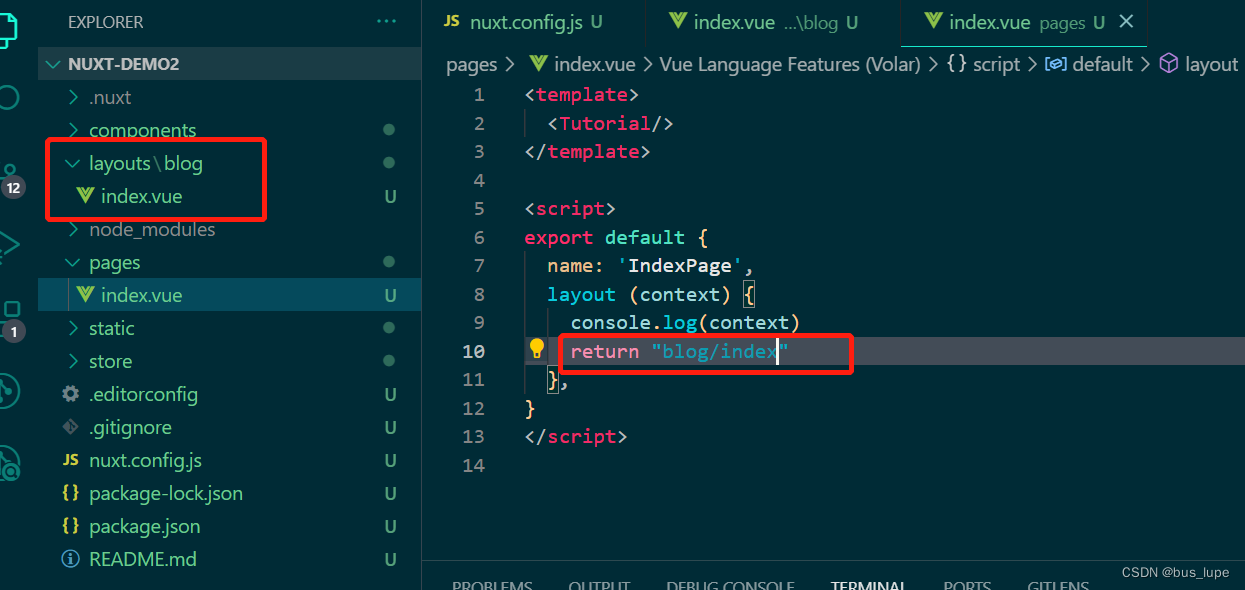
8.自定义组件布局和详解Context上下文
pages/index.vue layout布局运行在服务端 1、在项目的目录下新建layout文件夹,并新建一个blog.vue布局文件 2、在页面中的layout函数里,返回刚才新建布局文件的名字blog就可以使用了 export default {...layout (context) {console.log(context)retu…...
几个Web自动化测试框架的比较:Cypress、Selenium和Playwright
介绍:Web自动化测试框架对于确保Web应用程序的质量和可靠性至关重要。它们帮助开发人员和测试人员自动执行重复性任务,跨多个浏览器和平台执行测试,并在开发早期发现问题。 以下仅代表作者观点: 本文探讨来3种流行的Web自动化测…...
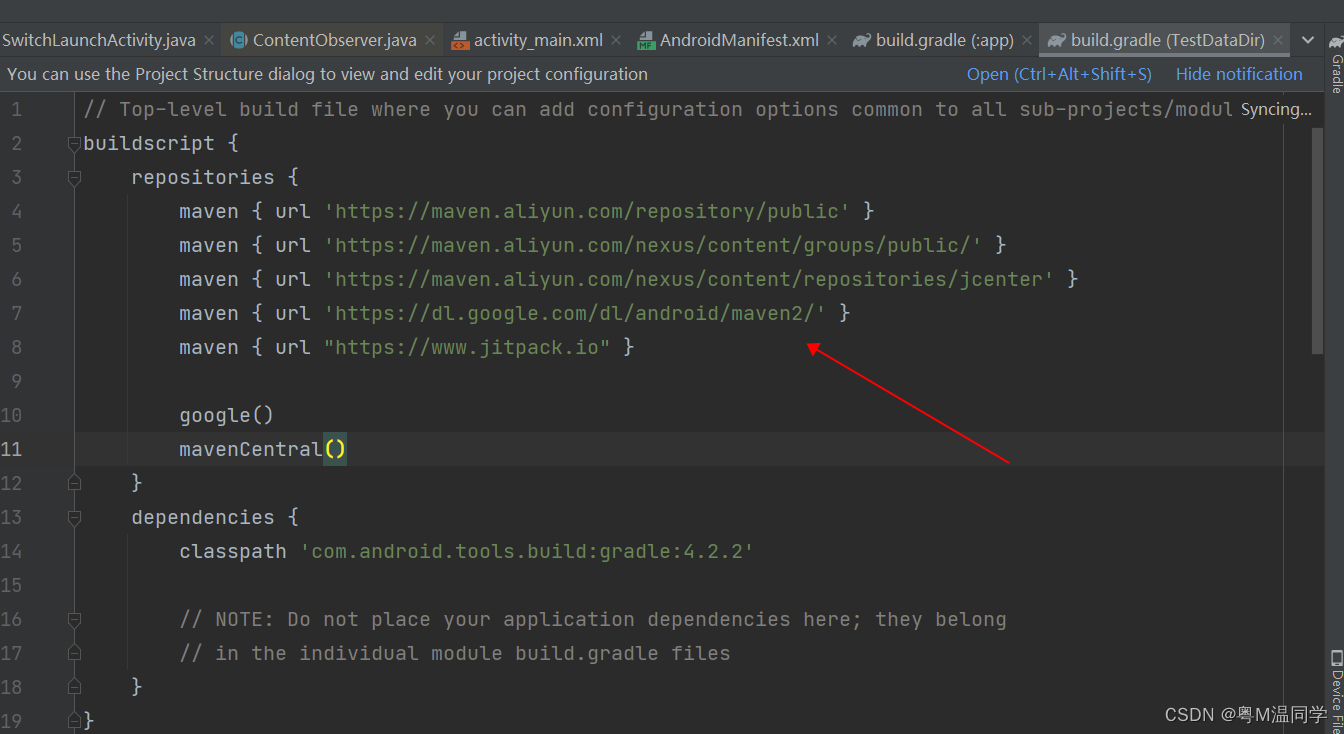
Android Studio中配置aliyun maven库
当下载第三方库失败的时候,通过Android Studio中配置aliyun maven库,达到正常下载库效果 在项目的根build.gradle里面(不是module)buildscriptde对应位置添加配置: maven { url https://maven.aliyun.com/repository/…...

记录使用阿里 ARoute 遇到的坑
1.按照官方一个配置好之后 尝试使用 跳转出现 Aroute Theres no route matched path"" 我这边遇到的坑是配置问题 kotiln 使用了 Java的配置 plugins {id("com.android.application")id("org.jetbrains.kotlin.android")id("kotlin-kapt&…...

lesson2(补充)关于const成员函数
个人主页:Lei宝啊 愿所有美好如期而遇 前言: 将const 修饰的 “ 成员函数 ” 称之为 const 成员函数 , const 修饰类成员函数,实际修饰该成员函数 隐含的 this 指针 ,表明在该成员函数中不能对类的任何成员进行修改…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...