javascript中各种风骚的代码
1.判断数值符号是否相同
function numericSymbolsIsEqual(x: number, y: number): boolean {return (x ^ y) >= 0}console.log(numericSymbolsIsEqual(1, 1))console.log(numericSymbolsIsEqual(-1, 1))console.log(numericSymbolsIsEqual(1, -1))console.log(numericSymbolsIsEqual(-1, -1))
输出如下
判断一个数n是否为2的整数幂
代码部分
function isPowerOfTwo(n: number): boolean {return (n & (n - 1)) === 0}console.log(isPowerOfTwo(4))console.log(isPowerOfTwo(5))console.log(isPowerOfTwo(6))console.log(isPowerOfTwo(1024))console.log(isPowerOfTwo(1021))
输出如下
星级评分
enum Score {veryPoor = 1,poor,ordinary,good,veryGood
}
function starRating(n: Score): string {return '★★★★★☆☆☆☆☆'.slice(5 - n, 10 - n)
}
console.log(starRating(Score.veryPoor))
console.log(starRating(Score.poor))
console.log(starRating(Score.ordinary))
console.log(starRating(Score.good))
console.log(starRating(Score.veryGood))
输出如下

0和1切换
function toggle(n: number): number {return n ^= 1}console.log(toggle(1))console.log(toggle(1))console.log(toggle(0))console.log(toggle(0))console.log(toggle(1))
浮点数向下取整
function roundDownDoubleNon(n: number): number {return ~~n}function roundDownRightShift(n: number): number {return n >> 0}function roundDownLeftShift(n: number): number {return n << 0}function roundDownOr(n: number): number {return n | 0}console.log(roundDownDoubleNon(Math.PI))console.log(roundDownRightShift(Math.PI))console.log(roundDownLeftShift(Math.PI))console.log(roundDownOr(Math.PI))

x乘2的y次幂
function getTwoYPower(x: number, y: number): number {return x << y}// 输出1乘2的2次方console.log(getTwoYPower(1, 2))// 输出2乘2的3次方console.log(getTwoYPower(2, 3))// 输出3乘2的2次方console.log(getTwoYPower(3, 2))

让天底下的代码再也没有bug
try {//code} catch (error) {location.href = `https://baidu.com/esarch?q=js+${error.message}`}
这个就不做演示啦哈
相关文章:

javascript中各种风骚的代码
1.判断数值符号是否相同 function numericSymbolsIsEqual(x: number, y: number): boolean {return (x ^ y) > 0}console.log(numericSymbolsIsEqual(1, 1))console.log(numericSymbolsIsEqual(-1, 1))console.log(numericSymbolsIsEqual(1, -1))console.log(numericSymbols…...

el-tree横向纵向滚动条
el-tree未展开时样式 el-tree展开时样式 给容器一个高度,然后样式加上overflow: scroll,这样纵向滚动条就出来了。 <el-card style"height: 528px;overflow: scroll"><el-inputplaceholder"输入关键字进行过滤"v-model&…...

STM32G030F6P6 芯片实验 (一)
STM32G030F6P6 芯片实验 (一) 淘宝搞了几片, 没试过 G系列, 试试感觉. 先搞片小系统版: 套 STM32F103C8T6小系统板格式. 原理图: (1) Ref 有点跳, 从 STM32F103C8T6 系统板改的, 没重编号. (2) Type-C 纯给电, 砍了 16pin的, 直接换 6pin的。 (3) 测试LED放 B2。 (4) 测试底…...
Wpf 使用 Prism 实战开发Day01
一.开发环境准备 1. VisualStudio 2022 2. .NET SDK 7.0 3. Prism 版本 8.1.97 以上环境,如有新的版本,可自行选择安装新的版本为主 二.创建Wpf项目 1.项目的名称:MyToDo 项目名称:这里只是记录学习,所以随便命名都无所谓,只要觉得合理就…...

6G关键新兴技术- 智能超表面(RIS)技术演进
摘要: 根据欧盟5G公私联盟协会定义,可重构智慧表面技术是由能够任意塑造电磁波面的材料组成,几乎是被动设备,可以适应或改变发射器和接收器之间的无线电信号。 一、产品定义及范围 根据欧盟5G公私联盟协会(5G Infrastructure P…...
【redhat9.2】搭建Discuz-X3.5网站
步骤 1.配置软件仓库 2.安装对应的软件 httpd php* mariadb* 3.启动服务 httpd mariadb 4.配置数据库 创建数据库 修改root密码 数据库的 5.传源码包(Discuz-X3.5) 解压 6.web页面初始化 关闭防火墙 允许http服务通过 修改权限 实…...

算法篇 : 并查集
介绍 英文名:union find set 作用:合并集合,查询集合 合并:将有直接关系的顶点放在一个集合里面 查找:查询某个顶点所属的集合 集合的标志:用祖先点的标号作为每个集合的标识 案例 如果说将下图的集合2合并…...

AM@微积分基本定理@微积分第二基本定理
文章目录 abstract微积分第二基本定理微积分基本公式公式书写例 结合不定积分的方法求定积分定积分换元法证明 定积分换元公式逆用例 和不定积分第二类换元法的差别定积分分部积分法例 abstract 微积分第一基本定理告诉我们,总是能够通过积分法构造(表达)一个连续函数的原函数…...

goland常用快捷键
移动光标 控制光标的移动:fn上下左右 移至当前页的页头:ctrlPgUp 移至并选中光标到当前页头:ctrlshiftPgUp 移至当前页的页尾:ctrlPgDn 移至并选中当前光标到当前页尾:ctrlshiftPgDn 返回到当前的光标处…...

CSDN写文章时常见问题及技巧
CSDN写文章时常见问题及技巧 1.有序待续、更新中 1.有序 过程: 写 1.空格 ,注意“.”后加个空格就可以生成序号,随心所欲编辑了 待续、更新中 ————————————————————— 以上就是今日博客的全部内容了 创作不易,若对您有…...
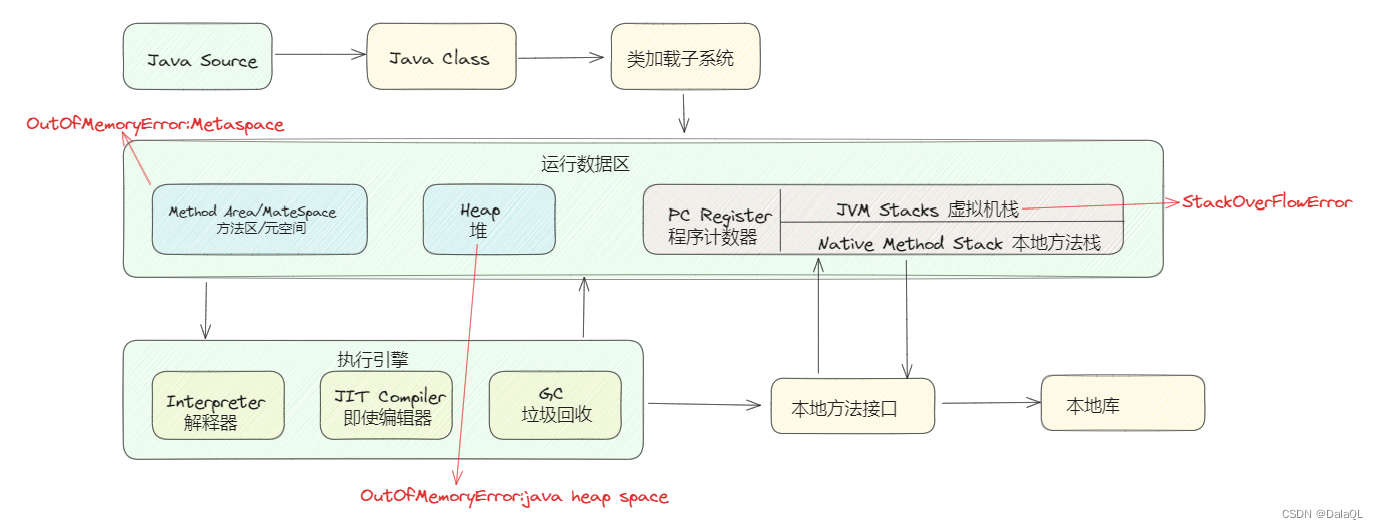
JVM虚拟机详解
目录 01JVM由哪些部分组成/运行流程 什么是程序计数器 详细介绍堆 介绍方法区(Method Area) 直接内存 虚拟机栈(Java Virtual machine Stacks) 垃圾回收是否涉及栈内存 栈内存分配越大越好吗 方法内的局部变量是否线程安全 什么情况下会导致栈…...

Go 怎么操作 OSS 阿里云对象存储
1 介绍 在项目开发中,我们经常会使用对象存储,比如 Amazon 的 S3,腾讯云的 COS,阿里云的 OSS 等。本文我们以阿里云 OSS 为例,介绍怎么使用 Go 操作对象存储。 阿里云 OSS 提供了 REST Api 和 OSS Go SDK࿰…...

vue3 Suspense组件
在 Vue 3 中,<Suspense> 组件用于处理异步组件加载时的等待状态和错误处理。它允许你在加载异步组件时显示一个自定义的加载指示器,以及在加载失败时显示错误信息。以下是一个详细的 <Suspense> 组件的使用示例: 首先࿰…...

NlogPrismWPF
文章目录 Nlog&Prism&WPF日志模块实现原理添加配置注入服务应用测试其他模块怎么调用? Nlog&Prism&WPF 日志模块 介绍了为WPF框架Prism注册Nlog日志服务的方法 实现原理 无论是在WPF或者ASP.NET Core当中, 都可以使用ServiceCollection来做到着…...
, 文件上传实战绕过思路, 基础篇)
文件上传漏洞(2), 文件上传实战绕过思路, 基础篇
文件上传漏洞实战思路(基础) 准备一句话木马文件 mm.php 一, 前端绕过 p1 浏览器禁用js先把mm.php后缀名修改为mm.jpg, 点击提交后, 用 burp 截取请求, 将数据包中的文件名修改回mm.php再提交. 二, 类型MIME绕过 p2 使用 burp 修改 Content-Type: image/jpeg 三, 黑名单绕…...
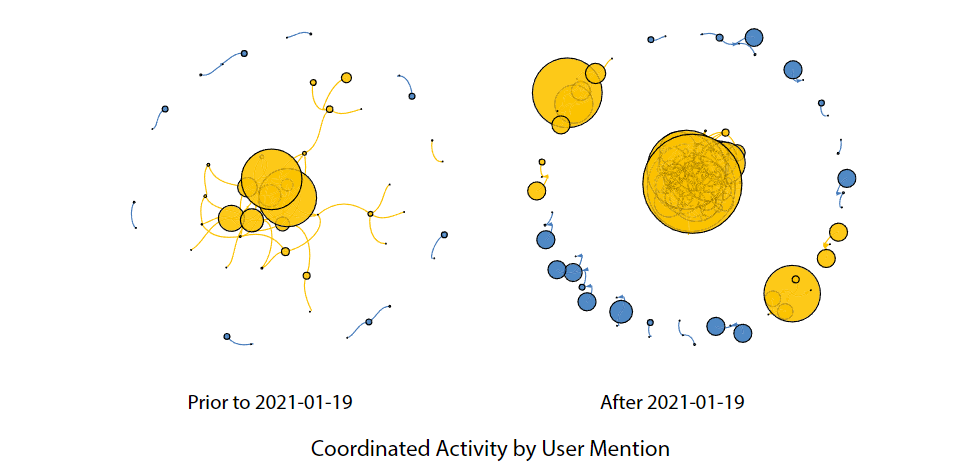
论文阅读 - Hidden messages: mapping nations’ media campaigns
论文链接: https://link.springer.com/content/pdf/10.1007/s10588-023-09382-7.pdf 目录 1 Introduction 2 The influence model 2.1 The influence‑model library 3 Data 4 Methodology 4.1 Constructing observations 4.2 Learning the state‑transiti…...

[AutoSAR系列] 1.3 AutoSar 架构
依AutoSAR及经验辛苦整理,原创保护,禁止转载。 专栏 《深入浅出AutoSAR》 1. 整体架构 图片来源: AutoSar 官网 从官往图中可以看出autosar作为汽车ECU软件架构,是通过分层来实现软硬件隔离。就像大多数操作系统一样ÿ…...
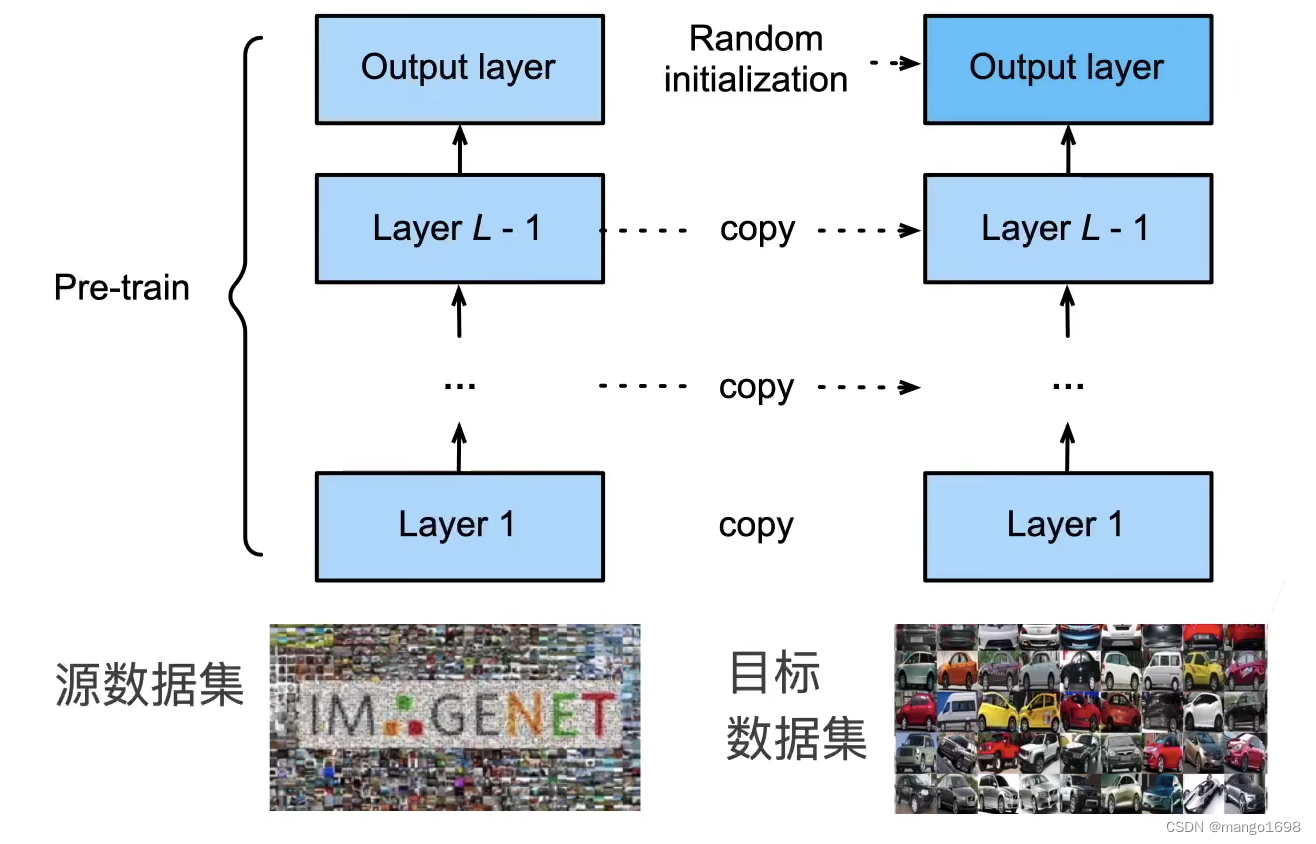
迁移学习 - 微调
什么是与训练和微调? 你需要搭建一个网络模型来完成一个特定的图像分类的任务。首先,你需要随机初始化参数,然后开始训练网络,不断调整参数,直到网络的损失越来越小。在训练的过程中,一开始初始化的参数会…...

09 用户态跟踪:如何使用eBPF排查应用程序?
09 用户态跟踪:如何使用eBPF排查应用程序? sudo bpftrace -e usdt:/usr/bin/python3:function__entry { printf("%s:%d %s\n", str(arg0), arg2, str(arg1))} # -*- coding: UTF-8 -*- import socket from socket import SOL_SOCKET, SO_R…...
深入浅出排序算法之堆排序
目录 1. 算法介绍 2. 执行流程⭐⭐⭐⭐⭐✔ 3. 代码实现 4. 性能分析 1. 算法介绍 堆是一种数据结构,可以把堆看成一棵完全二叉树,这棵完全二叉树满足:任何一个非叶结点的值都不大于(或不小于)其左右孩子结点的值。若父亲大孩子小&#x…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
