AM@微元法和定积分的应用@平面图形面积@立体体积@曲线弧长
文章目录
- abstract
- 微元法
- 平面图形的面积
- 极坐标上图形面积
- 曲边扇形面积
- 平行截面面积为已知的立体体积
- 旋转体的体积
- 绕 x x x轴旋转
- 绕 y y y轴旋转
- 另一类型旋转体积
- 曲线弧长
- 参数方程表示的曲线弧长
- 直角坐标方程表示的曲线弧长
- 极坐标方程表示得曲线弧长
- 小结
abstract
- 微元法
- 定积分的应用平面图形面积@立体体积@曲线弧长
微元法
- 定积分(一重,二重,三重积分)应用的关键在于微元法
- 设所求的量 F F F依赖于区间 [ a , b ] [a,b] [a,b]以及在此区间上定义的某函数 f ( x ) f(x) f(x),且满足
- 当 f ( x ) f(x) f(x)为常数 C C C时, F = C ⋅ ( b − a ) F=C\cdot{(b-a)} F=C⋅(b−a)
- 当 [ a , b ] [a,b] [a,b]分为一些小区间 Δ x \Delta{x} Δx之和时,量 F F F也被分割为相应的一些 Δ F \Delta{F} ΔF之和,即 F F F具有可加性
- 将 f ( x ) f(x) f(x)在小区间 [ x , x + Δ x ] [x,x+\Delta{x}] [x,x+Δx]上视为常量,于是由微分学有,近似
- Δ F ≈ f ( x ) Δ x \Delta{F}\approx{f(x)}\Delta{x} ΔF≈f(x)Δx
(1),或更准确表示为: Δ F \Delta{F} ΔF= f ( x ) Δ x + o ( Δ x ) f(x)\Delta{x}+o(\Delta{x}) f(x)Δx+o(Δx), ( Δ x → 0 ) (\Delta{x}\to{0}) (Δx→0)(2) - 从而 d F \mathrm{d}F dF= f ( x ) d x f(x)\mathrm{d}x f(x)dx
(3),两边做 [ a , b ] [a,b] [a,b]上的积分,即 F = ∫ a b f ( x ) d x F=\int_{a}^{b}f(x)\mathrm{d}x F=∫abf(x)dx
- Δ F ≈ f ( x ) Δ x \Delta{F}\approx{f(x)}\Delta{x} ΔF≈f(x)Δx
- 式(1)或(2)称为取微元,式(3)称为** F F F的微元**
- 微元法的步骤为:划分,近似,求和,逼近
平面图形的面积
- 曲线 y = y 2 ( x ) y=y_2(x) y=y2(x)和 y = y 1 ( x ) y=y_1(x) y=y1(x),( y 2 ( x ) ⩾ y 1 ( x ) y_2(x)\geqslant{y_1(x)} y2(x)⩾y1(x))以及 x = a , x = b x=a,x=b x=a,x=b围成的平面图形的面积 S = ∫ a b ( y 2 ( x ) − y 1 ( x ) ) d x S=\int_{a}^{b}(y_2(x)-y_1(x))\mathrm{d}x S=∫ab(y2(x)−y1(x))dx
- 曲线 x = x 2 ( y ) x=x_2(y) x=x2(y)和 x = x 1 ( y ) x=x_1(y) x=x1(y),( x 2 ( y ) ⩾ x 1 ( y ) x_2(y)\geqslant{x_1(y)} x2(y)⩾x1(y))以及 y = c , y = d y=c,y=d y=c,y=d围成的平面图形面积为 S = ∫ c d ( x 2 ( y ) − x 1 ( y ) ) d y S=\int_{c}^{d}(x_2(y)-x_1(y))\mathrm{d}y S=∫cd(x2(y)−x1(y))dy
- 极坐标曲线 r = r ( θ ) r=r(\theta) r=r(θ)介于两射线 θ = α \theta=\alpha θ=α与 θ = β \theta=\beta θ=β, ( 0 < β − α ⩽ 2 π ) (0<\beta-\alpha\leqslant{2\pi}) (0<β−α⩽2π)之间的曲边扇形的面积为 S = 1 2 ∫ α β r 2 ( θ ) d θ S=\frac{1}{2}\int_{\alpha}^{\beta}r^2(\theta)\mathrm{d}\theta S=21∫αβr2(θ)dθ
- 由参数方程: x = x ( t ) x=x(t) x=x(t), y = y ( t ) y=y(t) y=y(t), ( α ⩽ t ⩽ β ) (\alpha\leqslant{t}\leqslant\beta) (α⩽t⩽β)所围成平面图形的面积为 S = ∫ α β ∣ y ( t ) x ′ ( t ) ∣ d t S=\int_{\alpha}^{\beta}|y(t)x'(t)|\mathrm{d}t S=∫αβ∣y(t)x′(t)∣dt或 S = ∫ α β ∣ x ( t ) y ′ ( t ) ∣ d t S=\int_{\alpha}^{\beta}|x(t)y'(t)|\mathrm{d}t S=∫αβ∣x(t)y′(t)∣dt
- 某些曲线方程的显函数形式不易表示,可考虑使用参数方程表示,并利用换元积分法的方法对参数方程确定的曲线相关图形的面积进行定积分计算
- 例如椭圆 x = a cos t x=a\cos{t} x=acost, y = b sin t y=b\sin{t} y=bsint的面积,即椭圆 x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 a2x2+b2y2=1在第一象限的面积,是整个椭圆面积 S S S的 1 4 \frac{1}{4} 41, S = 4 ∫ 0 a y d x S=4\int_{0}^{a}y\mathrm{d}x S=4∫0aydx
- 当 x x x从 0 → a 0\to{a} 0→a时,即 a cos t a\cos{t} acost从 0 → a 0\to{a} 0→a,即 cos t \cos{t} cost从而 0 → 1 0\to{1} 0→1,所以 t t t从 π 2 → 0 \frac{\pi}{2}\to{0} 2π→0可作为换元后的积分限
- = 4 ∫ π 2 0 b sin t ⋅ ( − a ) sin t d t 4\int_{\frac{\pi}{2}}^{0}b\sin{t}\cdot{(-a)\sin{t}}\mathrm{d}t 4∫2π0bsint⋅(−a)sintdt= 4 a b ∫ 0 π 2 sin 2 t d t 4ab\int_{0}^{\frac{\pi}{2}}\sin^2{t}\mathrm{d}t 4ab∫02πsin2tdt 对调积分限
- = 4 a b ( 1 2 ( t − 1 2 sin 2 t ) ) ∣ 0 π 2 4ab(\frac{1}{2}(t-\frac{1}{2}\sin{2t}))|_{0}^{\frac{\pi}{2}} 4ab(21(t−21sin2t))∣02π= π a b \pi{ab} πab
极坐标上图形面积
曲边扇形面积
-
曲边扇形:普通扇形(或称为圆弧扇形或圆扇形)的圆弧改为一般曲线弧后的图形
- 一般默认扇形指的是圆扇形
-
对于极坐标曲线方程 r = r ( θ ) r=r(\theta) r=r(θ),自变量为极角 θ \theta θ,因变量为 r r r
-
假设 r ( θ ) r(\theta) r(θ)在区间 [ α , β ] [\alpha,\beta] [α,β]上连续, r ( θ ) ⩾ 0 r(\theta)\geqslant{0} r(θ)⩾0,求两射线 θ = α \theta=\alpha θ=α与 θ = β \theta=\beta θ=β, ( 0 < β − α ⩽ 2 π ) (0<\beta-\alpha\leqslant{2\pi}) (0<β−α⩽2π)以及 r = r ( θ ) r=r(\theta) r=r(θ)所围成的曲边扇形的面积 S S S
-
这个问题的计算公式可以通过定积分的定义推导
- 设区间 [ α , β ] [\alpha,\beta] [α,β]分为 n n n个部分区间,并构成 n n n个区间的 n + 1 n+1 n+1个分点为 α = θ 0 < θ 1 < ⋯ < θ n = β \alpha=\theta_0<\theta_1<\cdots<\theta_{n}=\beta α=θ0<θ1<⋯<θn=β
- 记 Δ θ i \Delta{\theta}_{i} Δθi= θ i − θ i − 1 \theta_i-\theta_{i-1} θi−θi−1, ( i = 1 , 2 , ⋯ , n ) (i=1,2,\cdots,n) (i=1,2,⋯,n);取 λ = max 1 ⩽ i ⩽ n { Δ θ i } \lambda=\max\limits_{1\leqslant{i}\leqslant{n}}\set{\Delta\theta_{i}} λ=1⩽i⩽nmax{Δθi}
- 在每个部分区间内,任取一点 ξ i \xi_i ξi,(或记为 θ ‾ i \overline{\theta}_{i} θi)
- 那么以 ξ i \xi_i ξi为半径,以射线 θ = θ i − 1 \theta=\theta_{i-1} θ=θi−1和 θ = θ i \theta=\theta_i θ=θi为两个边作圆扇形 O A B OAB OAB
- 将这些小扇形的面积相加,的和式: S 1 S_1 S1= ∑ i = 1 n 1 2 [ r ( ξ i ) ] 2 Δ θ i \sum_{i=1}^{n}\frac{1}{2}[r(\xi_i)]^2\Delta{\theta_{i}} ∑i=1n21[r(ξi)]2Δθi= ∑ i = 1 n 1 2 r 2 ( ξ i ) Δ θ i \sum_{i=1}^{n}\frac{1}{2}r^2(\xi_i)\Delta{\theta_{i}} ∑i=1n21r2(ξi)Δθi,其正好是 f ( θ ) = 1 2 [ r ( θ ) ] 2 f(\theta)=\frac{1}{2}[r(\theta)]^2 f(θ)=21[r(θ)]2= 1 2 r 2 ( θ ) \frac{1}{2}{r^2(\theta)} 21r2(θ)在 [ α , β ] [\alpha,\beta] [α,β]上的积分和数
- λ \lambda λ越小, S 1 S_1 S1就越接近 S S S,由于 f ( θ ) f(\theta) f(θ)在 [ α , β ] [\alpha,\beta] [α,β]上连续,从而 lim λ → 0 ∑ i = 1 n 1 2 r 2 ( ξ i ) Δ θ i \lim\limits_{\lambda\to{0}}{\sum_{i=1}^{n}\frac{1}{2}r^2(\xi_i)\Delta{\theta_{i}}} λ→0lim∑i=1n21r2(ξi)Δθi= ∫ α β f ( θ ) d θ \int_{\alpha}^{\beta}f(\theta)\mathrm{d}\theta ∫αβf(θ)dθ= 1 2 ∫ α β r 2 ( θ ) d θ \frac{1}{2}\int_{\alpha}^{\beta}r^2(\theta)\mathrm{d}\theta 21∫αβr2(θ)dθ
- 从而的公式 S = 1 2 ∫ α β r 2 ( θ ) d θ S=\frac{1}{2}\int_{\alpha}^{\beta}r^2(\theta)\mathrm{d}\theta S=21∫αβr2(θ)dθ,就是曲边扇形的面积
-
进一步地,若要求出曲扇环,(这里指扇环的两条圆弧改为一般曲线弧后的图形)
- 结合曲边扇形的描述,用极坐标描述这个图形为:两个直边重合的曲边扇形面积之差
- 即,由射线 θ = α , θ = β \theta=\alpha,\theta=\beta θ=α,θ=β,曲线 r = r 1 ( θ ) r=r_1(\theta) r=r1(θ), r = r 2 ( θ ) r=r_2(\theta) r=r2(θ), ( r 2 ( θ ) ⩽ r 1 ( θ ) ) (r_2(\theta)\leqslant r_1(\theta)) (r2(θ)⩽r1(θ))所围成的图形面积为 S = 1 2 ∫ α β r 1 2 ( θ ) d θ S=\frac{1}{2}\int_{\alpha}^{\beta}r_1^2(\theta)\mathrm{d}\theta S=21∫αβr12(θ)dθ- 1 2 ∫ α β r 2 2 ( θ ) d θ \frac{1}{2}\int_{\alpha}^{\beta}r_2^2(\theta)\mathrm{d}\theta 21∫αβr22(θ)dθ= 1 2 ∫ α β [ r 1 2 ( θ ) − r 2 2 ( θ ) ] d θ \frac{1}{2}\int_{\alpha}^{\beta}[r_1^2(\theta)-r_2^2(\theta)]\mathrm{d}\theta 21∫αβ[r12(θ)−r22(θ)]dθ
平行截面面积为已知的立体体积
- 考虑夹在垂直于 x x x轴的两个(立体空间)平面 x = a x=a x=a和 x = b x=b x=b, ( a < b ) (a<b) (a<b)之间的立体 V V V的体积(其体积也不妨记为 V V V)
- 假定 [ a , b ] [a,b] [a,b]内任何一点处作垂直于 x x x轴的平面截立体V的面积为 A ( x ) A(x) A(x),且 A ( x ) A(x) A(x)是一个连续函数(为可以执行定积分计算作铺垫)
- 推导体积 V V V的过程也是采用微分法,利用定积分的定义推导公式
- 将 x x x轴上的 [ a , b ] [a,b] [a,b]区间划分为 n n n分,并设分点为 a = x 0 < x 1 < ⋯ < x n = b a=x_0<x_1<\cdots<x_n=b a=x0<x1<⋯<xn=b
- 第 i i i个小区间宽度为 Δ x i = x i − x i − 1 \Delta{x_i}=x_i-x_{i-1} Δxi=xi−xi−1, ( i = 1 , 2 , ⋯ , n ) (i=1,2,\cdots,n) (i=1,2,⋯,n)
- 并令 λ = max 1 ⩽ i ⩽ n { Δ x i } \lambda=\max\limits_{1\leqslant{i}\leqslant{n}}\set{\Delta{x_{i}}} λ=1⩽i⩽nmax{Δxi};过 x i x_i xi作垂直于 x x x轴的平面 x = x i x=x_i x=xi, i = 1 , 2 , ⋯ , n i=1,2,\cdots,n i=1,2,⋯,n,它们分别截立体V得到 n n n个小部分 V i V_i Vi,任取 ξ i ∈ ( x i − 1 , x i ) \xi_{i}\in{(x_{i-1},x_i)} ξi∈(xi−1,xi),即用底面积为 A ( ξ i ) A(\xi_i) A(ξi),厚度为 Δ x i \Delta{x}_i Δxi的薄片(体积为 A ( ξ i ) Δ x i A(\xi_i)\Delta{x}_{i} A(ξi)Δxi)的体积之和 ∑ i = 1 n A ( ξ i ) Δ x i \sum_{i=1}^{n}A(\xi_i)\Delta{x_i} ∑i=1nA(ξi)Δxi估计(逼近) V V V;
- 即 lim λ → 0 ∑ i = 1 n A ( ξ i ) Δ x i \lim\limits_{\lambda\to{0}}{\sum_{i=1}^{n}A(\xi_i)\Delta{x_i}} λ→0lim∑i=1nA(ξi)Δxi= ∫ a b A ( x ) d x \int_{a}^{b}A(x)\mathrm{d}x ∫abA(x)dx,因此 V = ∫ a b A ( x ) d x V=\int_{a}^{b}A(x)\mathrm{d}x V=∫abA(x)dx
(1)
旋转体的体积
- 旋转面:设有一块由连续曲线 y = f ( x ) y=f(x) y=f(x), ( f ( x ) ⩾ 0 ) (f(x)\geqslant{0}) (f(x)⩾0)以及直线 x = a , x = b x=a,x=b x=a,x=b, ( a < b ) (a<b) (a<b)与 x x x轴围成的曲边梯形记为 A A A
绕 x x x轴旋转
- 图形 A A A绕 x x x轴旋转一周而生成的一个旋转体 V x V_{x} Vx,显然垂直于 x x x轴的面截该立体得到的是圆盘,并且圆盘体积为 x x x的函数 A ( x ) A(x) A(x)= π f 2 ( x ) \pi{f^2(x)} πf2(x)
(2) - 此时问题转换为截面积已知的立体体积,将(2)式代入(1)式,得 V x V_{x} Vx= π ∫ a b f 2 ( x ) d x \pi\int_{a}^{b}f^2(x)\mathrm{d}x π∫abf2(x)dx
绕 y y y轴旋转
- 图形 A A A绕 y y y轴旋转一周而生成的一个旋转体 V y V_y Vy,可以考虑使用它套筒法取微元积分
- 即,用平行于 y y y轴的圆柱面去截此旋转体,截面为周长为 2 π x 2\pi{x} 2πx,高度为 f ( x ) f(x) f(x)的圆柱侧面,面积记为 A ( x ) A(x) A(x)= 2 π x f ( x ) 2\pi{x}f(x) 2πxf(x)
(3) - 同样代入公式(1),的 V y V_y Vy= 2 π ∫ a b x f ( x ) d x 2\pi\int_{a}^{b}xf(x)\mathrm{d}x 2π∫abxf(x)dx
另一类型旋转体积
- 若构造曲边梯形的曲线为 x = ϕ ( y ) x=\phi(y) x=ϕ(y)形曲线,与直线 y = c , y = d y=c,y=d y=c,y=d, ( c < d ) (c<d) (c<d)以及 y y y轴构成的曲边梯形 B B B作为旋转面
- 绕 y y y轴旋转1周得到的立体体积应用类似于 A A A旋转面旋转的立体体积计算方法可得
- V y = π ∫ c d ϕ 2 ( y ) d y V_y=\pi\int_{c}^{d}\phi^2(y)\mathrm{d}y Vy=π∫cdϕ2(y)dy
曲线弧长
- 曲线弧长同样可以用微元法来求解
- 我们用曲线的内折线的长度来逼近被求曲线弧长
- 设平面上的曲线 l l l以 A , B A,B A,B为端点,在 l l l上任意取 n + 1 n+1 n+1个点: A = M 0 , M 1 , ⋯ , M n = B A=M_0,M_1,\cdots,M_n=B A=M0,M1,⋯,Mn=B,链接 M i − 1 , M i M_{i-1},M_i Mi−1,Mi, i = 1 , 2 , ⋯ , n i=1,2,\cdots,n i=1,2,⋯,n这些线段构成 l l l的内折线 l ′ l' l′
- 当 n n n不断增大, M i − 1 M i M_{i-1}M_i Mi−1Mi不断接近于0时,若 l ′ l' l′的长度趋近于于一个极限值,则这个极限值就定义为 l l l的长度;并且称此 l l l是可求长的
- 定理:光滑曲线弧是可求长的
参数方程表示的曲线弧长
- 设曲线 l l l弧由参数方程 x = ϕ ( t ) x=\phi(t) x=ϕ(t), y = ψ ( t ) y=\psi(t) y=ψ(t), ( t ∈ [ α , β ] ) (t\in[\alpha,\beta]) (t∈[α,β])给出
- 其中 ϕ ( t ) , ψ ( t ) \phi(t),\psi(t) ϕ(t),ψ(t)在 [ α , β ] [\alpha,\beta] [α,β]上具有连续导数, ϕ ′ ( t ) , ψ ′ ( t ) \phi'(t),\psi'(t) ϕ′(t),ψ′(t)不同时为0
- 取参数 t t t为积分变量其变化区间为 [ α , β ] [\alpha,\beta] [α,β],相应于 [ α , β ] [\alpha,\beta] [α,β]上任意小区间 [ t , t + d t ] [t,t+\mathrm{d}t] [t,t+dt]的小弧段的长度 Δ s \Delta{s} Δs近似等于对应的弦的长度 ( Δ x ) 2 + ( Δ y ) 2 \sqrt{(\Delta{x})^2+(\Delta{y})^2} (Δx)2+(Δy)2,
- 因为
- Δ x = ϕ ( t + d t ) − ϕ ( t ) ≈ d x \Delta{x}=\phi(t+\mathrm{d}t)-\phi(t)\approx{\mathrm{d}x} Δx=ϕ(t+dt)−ϕ(t)≈dx= ϕ ′ ( t ) d t \phi'(t)\mathrm{d}t ϕ′(t)dt
- Δ y = ψ ( t + d t ) − ψ ( t ) ≈ d y \Delta{y}=\psi(t+\mathrm{d}t)-\psi(t)\approx{\mathrm{d}y} Δy=ψ(t+dt)−ψ(t)≈dy= ψ ′ ( t ) d t \psi'(t)\mathrm{d}t ψ′(t)dt
- Δ s \Delta{s} Δs的近似值(弧微分),即弧长微元为 d s \mathrm{d}s ds= ( d x ) 2 + ( d y ) 2 \sqrt{(\mathrm{d}x)^{2}+(\mathrm{d}y)^2} (dx)2+(dy)2= ( ϕ ′ ( t ) d t ) 2 + ( ψ ′ ( t ) d t ) 2 \sqrt{(\phi'(t)\mathrm{d}t)^2+(\psi'(t)\mathrm{d}t)^2} (ϕ′(t)dt)2+(ψ′(t)dt)2= ϕ ′ 2 ( t ) + ψ ′ 2 ( t ) d t \sqrt{\phi'^2(t)+\psi'^2(t)}\mathrm{d}t ϕ′2(t)+ψ′2(t)dt
(0) - 所求弧长为 s = ∫ α β ϕ ′ 2 ( t ) + ψ ′ 2 ( t ) d t s=\int_{\alpha}^{\beta}\sqrt{\phi'^2(t)+\psi'^2(t)}\mathrm{d}t s=∫αβϕ′2(t)+ψ′2(t)dt
(1)
直角坐标方程表示的曲线弧长
- 设曲线弧由直角坐标方程 y = f ( x ) y=f(x) y=f(x), ( x ∈ [ a , b ] ) (x\in[a,b]) (x∈[a,b])给出
- 其中 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上具有一阶连续导数,此时曲线弧的参数方程表示为
(2)x = x x=x x=x; y = f ( x ) y=f(x) y=f(x), ( x ∈ [ a , b ] ) (x\in[a,b]) (x∈[a,b]),参数为 x x x - 从而问题转换为第一类问题,将方程组(2)代入(1),参数 t t t替换为 x x x;(积分变量 t t t替换为 x ) x) x),积分限替换为 [ a , b ] [a,b] [a,b],得 s = ∫ a b 1 + y ′ 2 d x s=\int_{a}^{b}\sqrt{1+y'^2}\mathrm{d}x s=∫ab1+y′2dx
(3)
极坐标方程表示得曲线弧长
- 可同样转换为参数方程类型
- 设曲线弧由极坐标 r = r ( θ ) r=r(\theta) r=r(θ), θ ∈ [ α , β ] \theta\in[\alpha,\beta] θ∈[α,β]给出,其中 r ( θ ) r(\theta) r(θ)在 [ α , β ] [\alpha,\beta] [α,β]上具有连续导数,则由直角坐标和极坐标转换公式可得该曲线弧的参数方程表示:
(4)- x = x ( θ ) = r ( θ ) cos θ x=x(\theta)=r(\theta)\cos{\theta} x=x(θ)=r(θ)cosθ, y = y ( θ ) = r ( θ ) sin θ y=y(\theta)=r(\theta)\sin\theta y=y(θ)=r(θ)sinθ, ( θ ∈ [ α , β ] ) (\theta\in[\alpha,\beta]) (θ∈[α,β])
- 这就是以极角 θ \theta θ为参数的曲线弧的参数方程
- 于是弧长微元由公式(0),得 d s \mathrm{d}s ds= x ′ 2 ( θ ) + y ′ 2 ( θ ) d θ \sqrt{x'^2(\theta)+y'^2(\theta)}\mathrm{d}\theta x′2(θ)+y′2(θ)dθ= [ r ′ ( θ ) cos θ − r ( θ ) sin θ ] 2 − [ r ′ ( θ ) sin θ + r ( θ ) cos θ ] 2 d θ \sqrt{[r'(\theta)\cos{\theta}-r(\theta)\sin\theta]^2-[r'(\theta)\sin\theta+r(\theta)\cos\theta]^2}\mathrm{d}\theta [r′(θ)cosθ−r(θ)sinθ]2−[r′(θ)sinθ+r(θ)cosθ]2dθ= r ′ 2 ( θ ) + r 2 ( θ ) d θ \sqrt{r'^2(\theta)+r^2(\theta)}\mathrm{d}\theta r′2(θ)+r2(θ)dθ
(5) - 从而所求弧长为 s = ∫ α β r ′ 2 ( θ ) + r 2 ( θ ) d θ s=\int_{\alpha}^{\beta}\sqrt{r'^2(\theta)+r^2(\theta)}\mathrm{d}\theta s=∫αβr′2(θ)+r2(θ)dθ
(6)
小结
- 参数方程表示曲线的能力最强,上述3种情形的后两种曲线形式都可以转换为参数方程形式,从而进一步推导出曲线不同表示方式下的曲线弧长公式
相关文章:

AM@微元法和定积分的应用@平面图形面积@立体体积@曲线弧长
文章目录 abstract微元法平面图形的面积极坐标上图形面积曲边扇形面积 平行截面面积为已知的立体体积旋转体的体积绕 x x x轴旋转绕 y y y轴旋转另一类型旋转体积 曲线弧长参数方程表示的曲线弧长直角坐标方程表示的曲线弧长极坐标方程表示得曲线弧长小结 abstract 微元法定积…...
SparkStreaming【实例演示】
前言 1、环境准备 启动Zookeeper和Kafka集群导入依赖: <dependency><groupId>org.apache.spark</groupId><artifactId>spark-core_2.12</artifactId><version>3.2.4</version></dependency><dependency>&l…...

提高抖音小店用户黏性和商品销量的有效策略
抖音小店是抖音平台上的电商模式,用户可以在抖音上购买各类商品。要提高用户黏性和商品销量,四川不若与众帮你整理了需要注意以下几个方面。 首先,提供优质的商品和服务。在抖音小店中,用户会通过观看商品展示视频和用户评价来选…...

提高公众意识:共同防范AI诈骗
随着人工智能技术的飞速发展,AI诈骗成为了一个不容忽视的威胁,影响到我们的社交、金融和个人隐私安全。在这个数字时代,提高公众对AI诈骗的意识至关重要,以下是一些关于如何提高公众意识以防范AI诈骗的观点: 认知AI诈…...

MES的物料管理
----物料管理的定义和作用---- 物料管理在制造执行系统(MES)中扮演着至关重要的角色。通过有效的物料管理,企业可以实现生产过程的高效性、准确性和可靠性,从而提高生产效率并降低成本。 一、物料管理的定义 物料管理是指对生产过…...
正点原子嵌入式linux驱动开发——Linux 多点电容触摸屏
随着智能手机的发展,电容触摸屏也得到了飞速的发展。相比电阻触摸屏,电容触摸屏有很多的优势,比如支持多点触控、不需要按压,只需要轻轻触摸就有反应。ALIENTEK的三款RGB LCD屏幕都支持多点电容触摸,本章就以ATK7016这…...
Git基础命令实践
文章目录 简介git的安装配置git的安装git的配置 git使用的基本流程创建版本库时光机穿梭版本回退工作区和暂存区管理修改撤销修改删除文件 远程仓库添加远程库从远程库克隆 总结 简介 本文主要记录了我在学习git操作的过程,以及如何使用GitHub。建议先参考廖雪峰的…...
微信小程序设计之页面文件pages
一、新建一个项目 首先,下载微信小程序开发工具,具体下载方式可以参考文章《微信小程序开发者工具下载》。 然后,注册小程序账号,具体注册方法,可以参考文章《微信小程序个人账号申请和配置详细教程》。 在得到了测…...
VScode 自定义主题各参数解析
参考链接: vscode自定义颜色时各个参数的作用(史上最全)vscode编辑器,自己喜欢的颜色 由于 VScode 搜索高亮是在是太不起眼了,根本看不到此时选中到哪个搜索匹配了,所以对此进行了配置,具体想增加更多可配置项可参考…...

Linux进程等待
文章目录 1. 为什么要进程等待2. 进程等待的方法waitwaitpid非阻塞轮询 1. 为什么要进程等待 子进程退出,如果父进程还未结束,没有管这个子进程,那么就可能会造成“僵尸进程”问题,进而出现内存泄漏 如果这个进程变成了“僵尸进程…...
python设计模式笔记1:创建型模式 工厂模式和抽象工厂模式
1.工厂模式 (1) 导入所需的模块( json 和 ElementTree )。 (2) 定义 JSON数据提取器类( JSONDataExtractor )。 (3) 定义 XML数据提取器类( XMLDataExtractor )。 (4) 添加工厂函数 dataextraction_factor…...

第五章 I/O管理 一、I/O设备的基本概念和分类
目录 一、什么是I/O设备 1、定义: 2、按特性分类: 3、按传输速率分类: 4、按信息交换的方式分类: 二、总结 一、什么是I/O设备 1、定义: I/O设备就是可以将数据输入到计算机,或者可以接收计算机输出…...
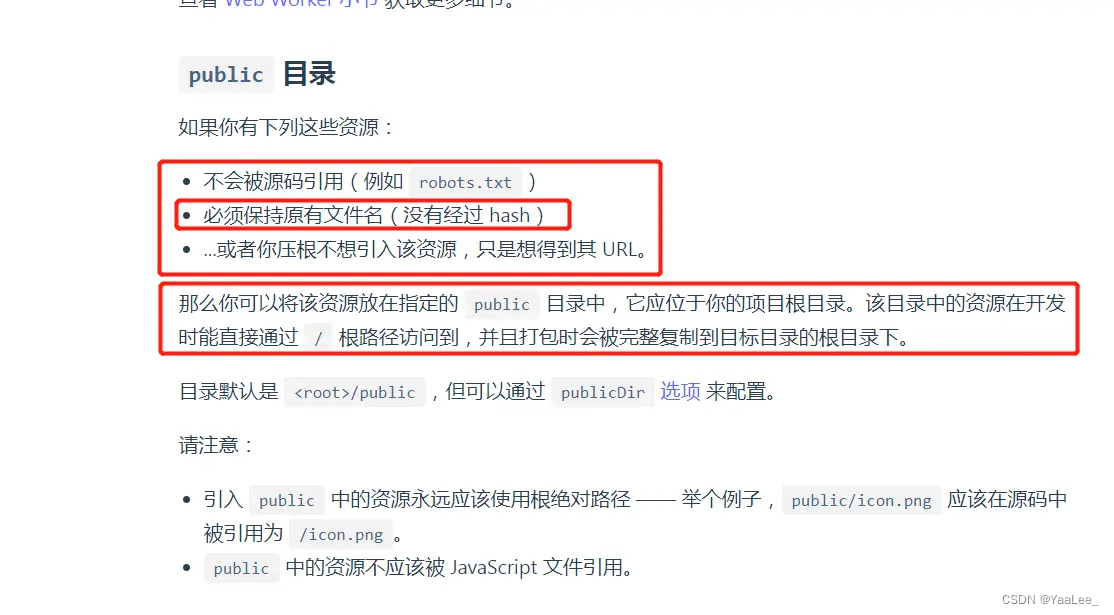
vue3动态引入图片(:src)
vite 官方默认的配置,如果资源文件在assets文件夹打包后会把图片名加上 hash值,但是直接通过 :src"imgSrc"方式引入并不会在打包的时候解析,导致开发环境可以正常引入,打包后却不能显示的问题 实际上我们不希望资源文…...
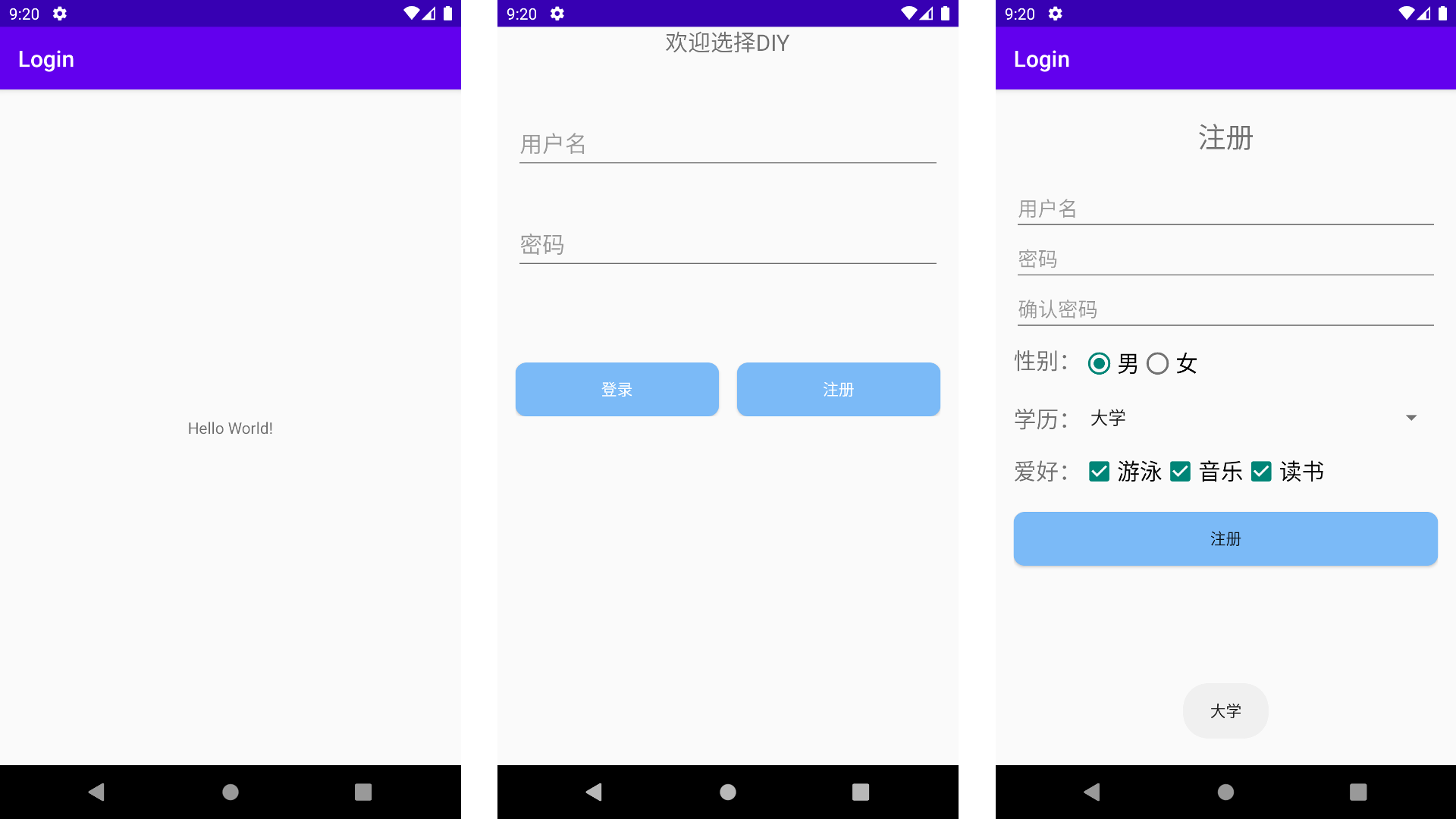
Android-登录注册页面(第三次作业)
第三次作业 - 登录注册页面 题目要求 嵌套布局。使用线性布局的嵌套结构,实现登录注册的页面。(例4-3) 创建空的Activity 项目结构树如下图所示: 注意:MainActivity.java文件并为有任何操作,主要功能集中…...
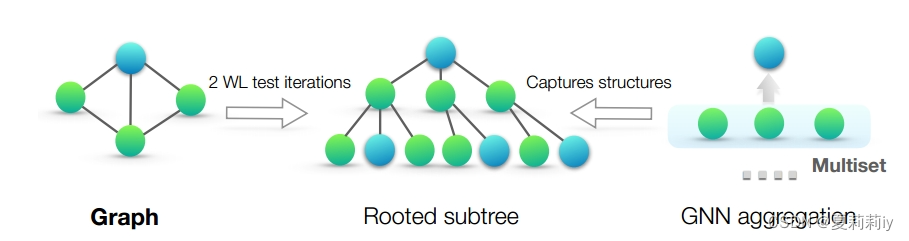
[论文精读]How Powerful are Graph Neural Networks?
论文原文:[1810.00826] How Powerful are Graph Neural Networks? (arxiv.org) 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记&#x…...

Redis实现分布式锁之----超时和失效(非原子性)问题----解决方案
Redis实现分布式锁之----超时和失效(非原子性)问题----解决方案 超时和失效(非原子性)问题 原子性问题:上锁时存入线程名称,删除时要先判断锁内的名称是不是自己的,是再删除,但是后…...

Android使用Hilt依赖注入,让人看不懂你代码
前言 之前接手的一个项目里有些代码看得云里雾里的,找了半天没有找到对象创建的地方,后来才发现原来使用了Hilt进行了依赖注入。Hilt相比Dagger虽然已经比较简洁,但对初学者来说还是有些门槛,并且网上的许多文章都是搬自官网&…...

ZYNQ连载01-ZYNQ介绍
ZYNQ连载01-ZYNQ介绍 1. ZYNQ 参考文档:《ug585-zynq-7000-trm.pdf》 ZYNQ分为PS和PL两大部分,PS即ARM,PL即FPGA,PL作为PS的外设。 2. 方案 ZYNQ7020为双核A9架构,多核处理器常用的运行模式为AMP(非对称多处理)和…...

第十节——Vue组件
一、什么是组件 组件(Component)是vue.js中很强大的一个功能,可以将一些可重用的代码进行封重用。 所有的Vue 组件同时也是Vue 的实例,可以接受使用相同的选项对象和提供相同的生命周期钩子。 一句话概括:组件就是可以扩展HTML元素ÿ…...

Redis(01)| 数据结构
这里写自定义目录标题 Redis 速度快的原因除了它是内存数据库,使得所有的操作都在内存上进行之外,还有一个重要因素,它实现的数据结构,使得我们对数据进行增删查改操作时,Redis 能高效的处理。 因此,这次我…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
