LeetCode 779. 第K个语法符号【递归,找规律,位运算】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
我们构建了一个包含 n 行( 索引从 1 开始 )的表。首先在第一行我们写上一个 0。接下来的每一行,将前一行中的0替换为01,1替换为10。
- 例如,对于
n = 3,第1行是0,第2行是01,第3行是0110。
给定行数 n 和序数 k,返回第 n 行中第 k 个字符。( k 从索引 1 开始)
示例 1:
输入: n = 1, k = 1
输出: 0
解释: 第一行:0
示例 2:
输入: n = 2, k = 1
输出: 0
解释:
第一行: 0
第二行: 01
示例 3:
输入: n = 2, k = 2
输出: 1
解释:
第一行: 0
第二行: 01
提示:
1 <= n <= 301 <= k <= 2^n - 1
解法 递归
首先题目给出一个 n n n 行的表(索引从 1 1 1 开始)。并给出表的构造规则为:第一行仅有一个 0 0 0,然后接下来的每一行可以由上一行中 0 0 0 替换为 01 01 01, 1 1 1 替换为 10 10 10 来生成。
- 比如当 n = 3 n = 3 n=3 时,第 1 1 1 行是 0 0 0,第 2 2 2 行是 01 01 01,第 3 3 3 行是 0110 0110 0110 。
现在要求表第 n n n 行中第 k k k 个数字, 1 ≤ k ≤ 2 n 1 \le k \le 2 ^ n 1≤k≤2n 。首先我们可以看到第 i i i 行中会有 2 i − 1 2^{i-1} 2i−1 个数字, 1 ≤ i ≤ n 1 \le i \le n 1≤i≤n ,且其中第 j j j 个数字按照构造规则会生第 i + 1 i + 1 i+1 行中的第 2 ∗ j − 1 2*j - 1 2∗j−1 和 2 ∗ j 2∗j 2∗j 个数字, 1 ≤ j ≤ 2 i − 1 1 \le j \le 2^{i-1} 1≤j≤2i−1 。
即对于第 i + 1 i + 1 i+1 行中的第 x x x 个数字 num 1 \textit{num}_1 num1 , 1 ≤ x ≤ 2 i 1 \le x \le 2^i 1≤x≤2i ,会被第 i i i 行中第 ⌊ x + 1 2 ⌋ \lfloor \frac{x + 1}{2} \rfloor ⌊2x+1⌋ 个数字 num 2 \textit{num}_2 num2 生成。且满足规则:
- 当 num 2 = 0 \textit{num}_2 = 0 num2=0 时, num 2 \textit{num}_2 num2 会生成 01 01 01:
num 1 = { 0 , x ≡ 1 ( m o d 2 ) 1 , x ≡ 0 ( m o d 2 ) \textit{num}_1 = \begin{cases} 0, & x \equiv 1 \pmod{2} \\ 1, & x \equiv 0 \pmod{2} \\ \end{cases} num1={0,1,x≡1(mod2)x≡0(mod2) - 当 n u m 2 = 1 num_2 = 1 num2=1 时, num 2 \textit{num}_2 num2 会生成 10 10 10:
num 1 = { 1 , x ≡ 1 ( m o d 2 ) 0 , x ≡ 0 ( m o d 2 ) \textit{num}_1 = \begin{cases} 1, & x \equiv 1 \pmod{2} \\ 0, & x \equiv 0 \pmod{2} \\ \end{cases} num1={1,0,x≡1(mod2)x≡0(mod2)
并且进一步总结我们可以得到: num 1 = ( x & 1 ) ⊕ 1 ⊕ num 2 \textit{num}_1 = (x \And 1) \oplus 1 \oplus \textit{num}_2 num1=(x&1)⊕1⊕num2 ,其中 & \And & 为「与」运算符, ⊕ \oplus ⊕ 为「异或」运算符。那么我们从第 n n n 不断往上递归求解,并且当在第一行时只有一个数字,直接返回 0 0 0 即可。
class Solution {
public:int kthGrammar(int n, int k) {if (n == 1) return 0;return (k & 1) ^ 1 ^ kthGrammar(n - 1, (k + 1) / 2);}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),其中 n n n 为题目给定表的行数,递归深度为 n n n。
- 空间复杂度: O ( n ) O(n) O(n),其中 n n n 为题目给定表的行数,主要为递归的空间开销。
解法2 找规律 + 递归
按照方法一,我们可以尝试写表中的前几行:
- 0 0 0
- 01 01 01
- 0110 0110 0110
- 01101001 0110 1001 01101001
- ⋯ \cdots ⋯
我们可以注意到规律:每一行的后半部分正好为前半部分的“翻转”——前半部分是 0 0 0 后半部分变为 1 1 1,前半部分是 1 1 1,后半部分变为 0 0 0。且每一行的前半部分和上一行相同。我们可以通过「数学归纳法」来进行证明。
有了这个性质,那么我们再次思考原问题:对于查询某一个行第 k k k 个数字,如果 k k k 在后半部分,那么原问题就可以转化为求解该行前半部分的对应位置的“翻转”数字,又因为该行前半部分与上一行相同,所以又转化为上一行对应对应的“翻转”数字。那么按照这样一直递归下去,并在第一行时返回数字 0 0 0 即可。
class Solution {
public:int kthGrammar(int n, int k) {if (k == 1) return 0;// 查询某一个行第k数,如果k在后半部分,可转化为求解该行前半部分对应位置的翻转数字if (k > (1 << (n - 2))) return 1 ^ kthGrammar(n - 1, k - (1 << (n - 2)));return kthGrammar(n - 1, k); // 一行前半部分和上一行相同}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),其中 n n n 为题目给定表的行数。
- 空间复杂度: O ( n ) O(n) O(n),其中 n n n 为题目给定表的行数,主要为递归的空间开销。
解法3 找规律 + 位运算
在「方法二」的基础上,我们来进行优化,本质上我们其实只需要求在过程中的“翻转”总次数,如果“翻转”为偶数次则原问题求解为 0 0 0 ,否则为 1 1 1。
首先我们修改行列的索引从 0 0 0 开始,此时原先第 p p p 行的索引现在为 p − 1 p - 1 p−1 行,第 i i i 行有 2 i 2 ^ i 2i 位。那么对于某一行 i i i 中下标为 x x x 的数字,如果 x < 2 i − 1 x < 2^{i - 1} x<2i−1 那么等价于求 i − 1 i - 1 i−1 行中下标为 x x x 的数字,否则 x x x 的二进制位的从右往左第 i i i 位(从第 0 0 0 位开始)为 1 1 1 ,此时需要减去该位(“翻转”一次),然后递归求解即可。所以我们可以看到最后“翻转”的总次数只和初始状态下的下标 x x x 二进制表示中 1 1 1 的个数有关。
因此原问题中求“翻转”的总次数,就等价于求 k − 1 k - 1 k−1 的二进制表示中 1 1 1 的个数。
class Solution {
public:int kthGrammar(int n, int k) {// return __builtin_popcount(k - 1) & 1;k--;int res = 0;while (k > 0) {k &= k - 1;res ^= 1;}return res;}
};
复杂度分析:
- 时间复杂度: O ( log k ) O(\log k) O(logk) ,其中 k k k 为题目给定查询的下标。
- 空间复杂度: O ( 1 ) O(1) O(1) ,仅使用常量变量。
相关文章:

LeetCode 779. 第K个语法符号【递归,找规律,位运算】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
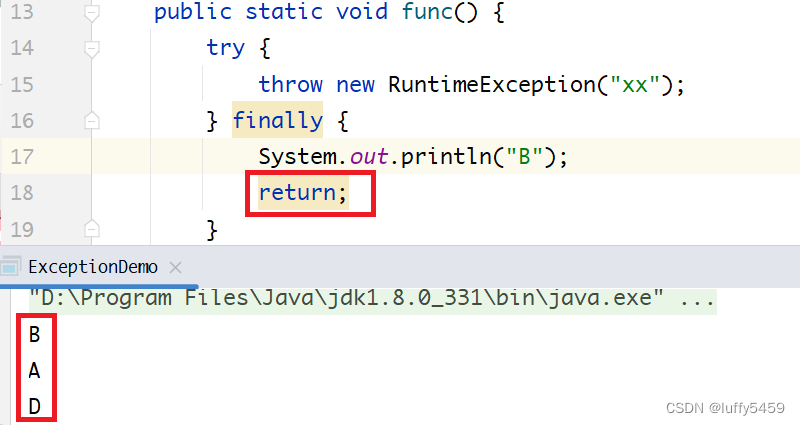
java try throw exception finally 遇上 return break continue造成异常丢失
如下所示,是一个java笔试题,考察的是抛出异常之后,程序运行结果,但是这里抛出异常,并没有捕获异常,而是通过finally来进行了流程控制处理。 package com.xxx.test;public class ExceptionFlow {public sta…...
+ Spring相关源码)
设计模式——装饰器模式(Decorator Pattern)+ Spring相关源码
文章目录 一、装饰器模式的定义二、个人理解举个抽象的例(可能并不是很贴切) 三、例子1、菜鸟教程例子1.1、定义对象1.2、定义装饰器 3、JDK源码 ——包装类4、JDK源码 —— IO、OutputStreamWriter5、Spring源码 —— BeanWrapperImpl5、SpringMVC源码 …...
MATLAB R2018b详细安装教程(附资源)
云盘链接: pan.baidu.com/s/1SsfNtlG96umfXdhaEOPT1g 提取码:1024 大小:11.77GB 安装环境:Win10/Win8/Win7 安装步骤: 1.鼠标右击【R2018b(64bit)】压缩包选择【解压到 R2018b(64bit)】 2.打开解压后的文件夹中的…...
GEE错误——影像加载过程中出现的图层无法展示的解决方案
问题: // I dont know if some standard value exists for the radius, in the same, I will assume that some software would prefer to use square shape, but circle makes more sense to me. // pixels is noice if you want to zoom in and out to visualize…...
读图数据库实战笔记03_遍历
1. Gremlin Server只将数据存储在内存中 1.1. 如果停止Gremlin Server,将丢失数据库里的所有数据 2. 概念 2.1. 遍历(动词) 2.1.1. 当在图数据库中导航时,从顶点到边或从边到顶点的移动过程 2.1.2. 类似于在关系数据库中的查…...

QT如何检测当前系统是是Windows还是Uninx或Mac?以及是哪个版本?
简介 通过Qt获取当前系统及版本号,需要用到QSysInfo。 QSysInfo类提供有关系统的信息。 WordSize指定了应用程序编译所在的平台的指针大小。 ByteOrder指定了平台是大端序还是小端序。 某些常量仅在特定的平台上定义。您可以使用预处理器符号Q_OS_WIN和Q_OS_MACOS来…...
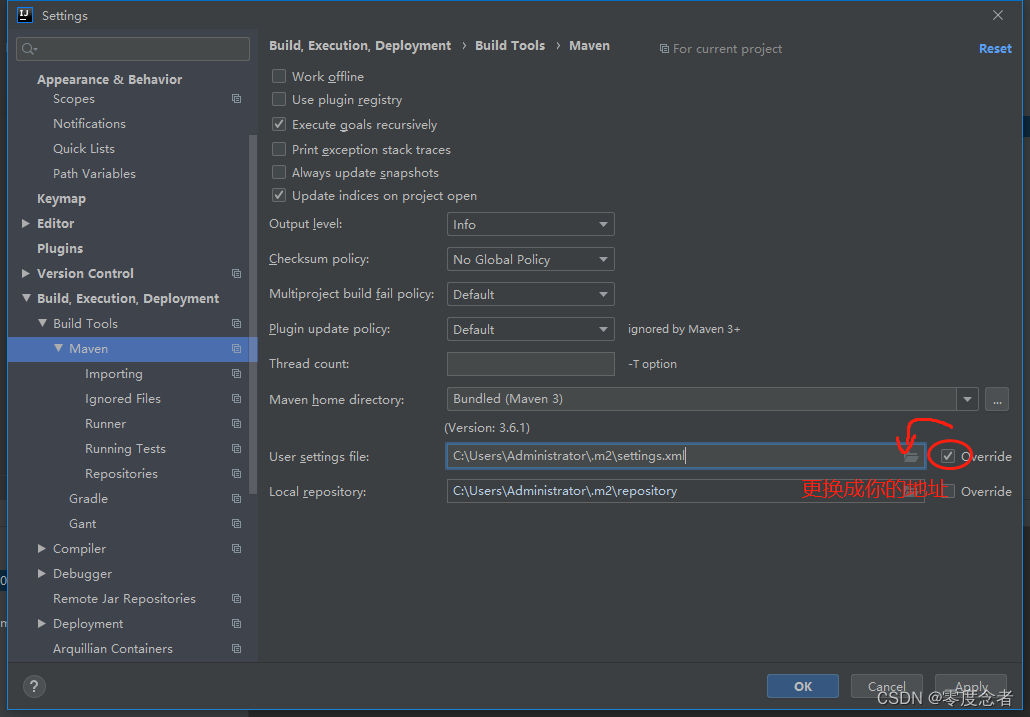
Maven配置阿里云中央仓库settings.xml
Maven配置阿里云settings.xml 前言一、阿里云settings.xml二、使用步骤1.任意目录创建settings.xml2.使用阿里云仓库 总结 前言 国内网络从maven中央仓库下载文件通常是比较慢的,所以建议配置阿里云代理镜像以提高jar包下载速度,IDEA中我们需要配置自己…...

由浅入深C系列八:如何高效使用和处理Json格式的数据
如何高效使用和处理JSON格式的数据 问题引入关于CJSON示例代码头文件引用处理数据 问题引入 最近的项目在用c处理后台的数据时,因为好多外部接口都在使用Json格式作为返回的数据结构和数据描述,如何在c中高效使用和处理Json格式的数据就成为了必须要解决…...
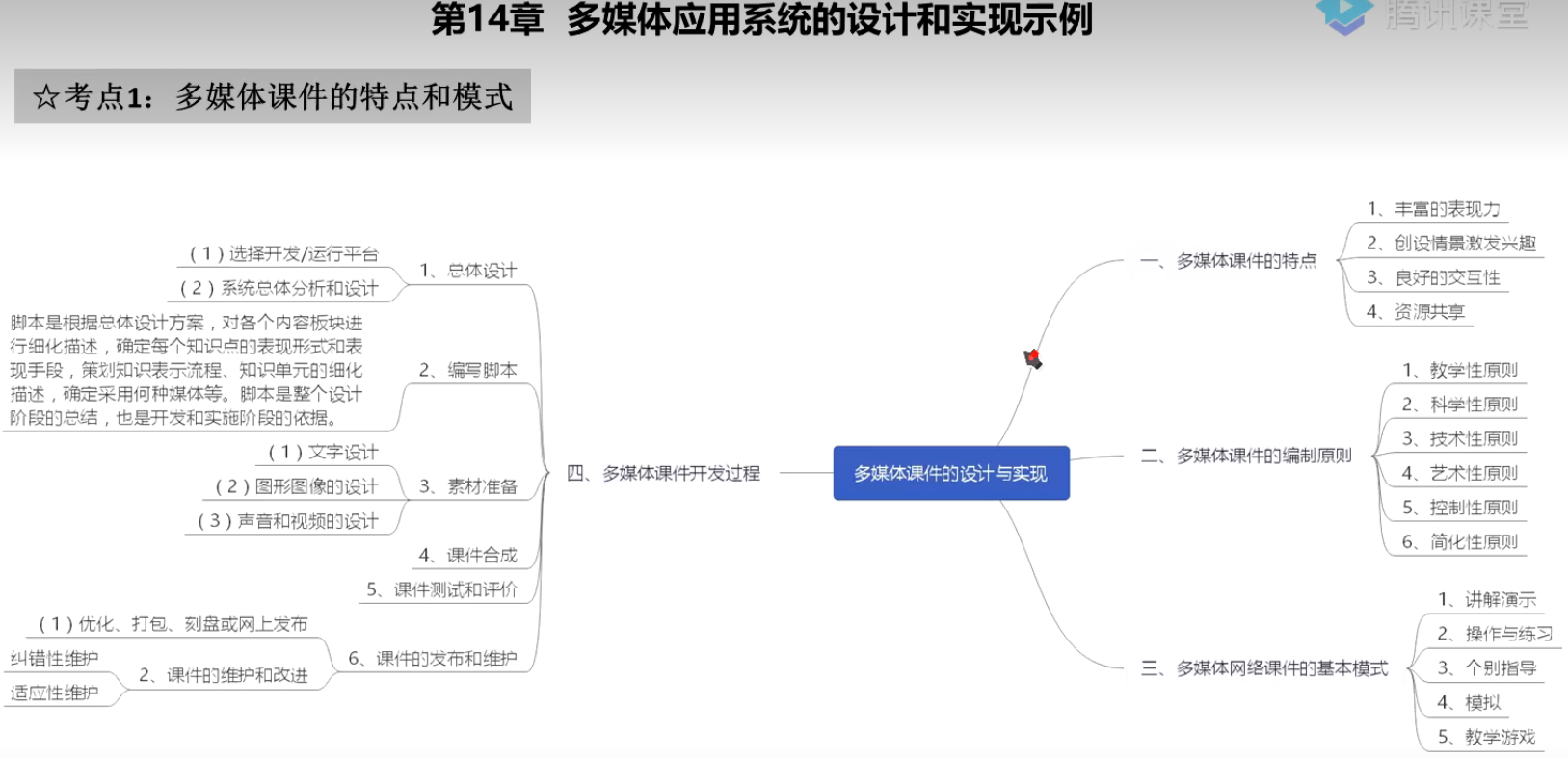
多媒体应用设计师 第16章 多媒体应用系统的设计和实现示例
口诀 思维导图 2020...

golang平滑重启库overseer实现原理
overseer主要完成了三部分功能: 1、连接的无损关闭,2、连接的平滑重启,3、文件变更的自动重启。 下面依次讲一下: 一、连接的无损关闭 golang官方的net包是不支持连接的无损关闭的,当主监听协程退出时,…...
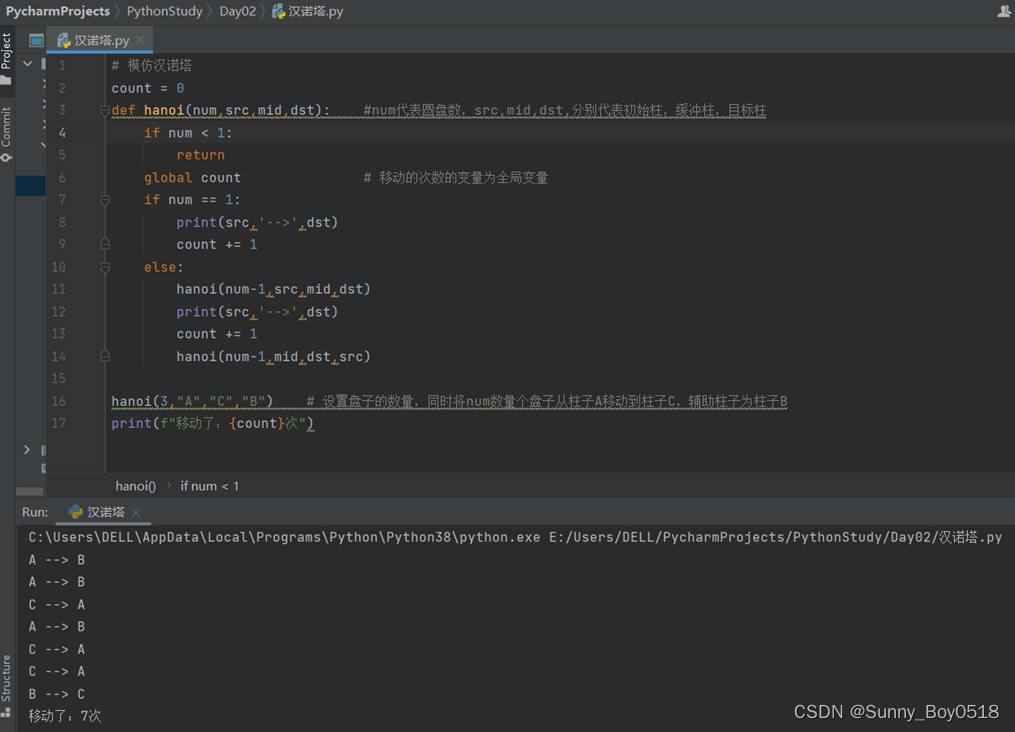
用Python定义一个函数,用递归的方式模拟汉诺塔问题
【任务需求】 定义一个函数,用递归的方式模拟汉诺塔问题,三个柱子,分别为A、B、C,其中A柱子上有N个盘子,从小到大编号为1到N,盘子大小不同。现在要将这N个盘子从A柱子移动到C柱子上,但移动的过…...

二手的需求
案例1030 某天项目经理小王,从用户现场带回了需求,以图形的方式,交给了产品经理。告诉他就照这样设计,结果是项目经理放弃让产品经理出效果图。 原因是产品经理觉得项目经理带回来的需求有问题。项目经理解释产品经理不接受&…...
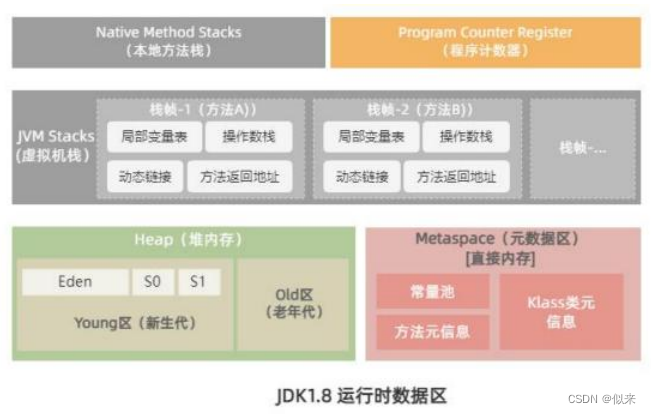
大厂面试题-JVM为什么使用元空间替换了永久代?
目录 面试解析 问题答案 面试解析 我们都知道Java8以及以后的版本中,JVM运行时数据区的结构都在慢慢调整和优化。但实际上这些变化,对于业务开发的小伙伴来说,没有任何影响。 因此我可以说,99%的人都回答不出这个问题。 但是…...
基本微信小程序的驾校宝典系统-驾照考试系统
项目介绍 系统模块分析是对系统的各个模块做出相应的说明以及解释。此系统的模块分别有用户模块、服务端模块和管理端模块这两大基本模块,其中服务端模块包括了首页、教练信息、教练咨讯、考试预约、我的等;而管理端模块则包括了个人中心、用户管理、教…...
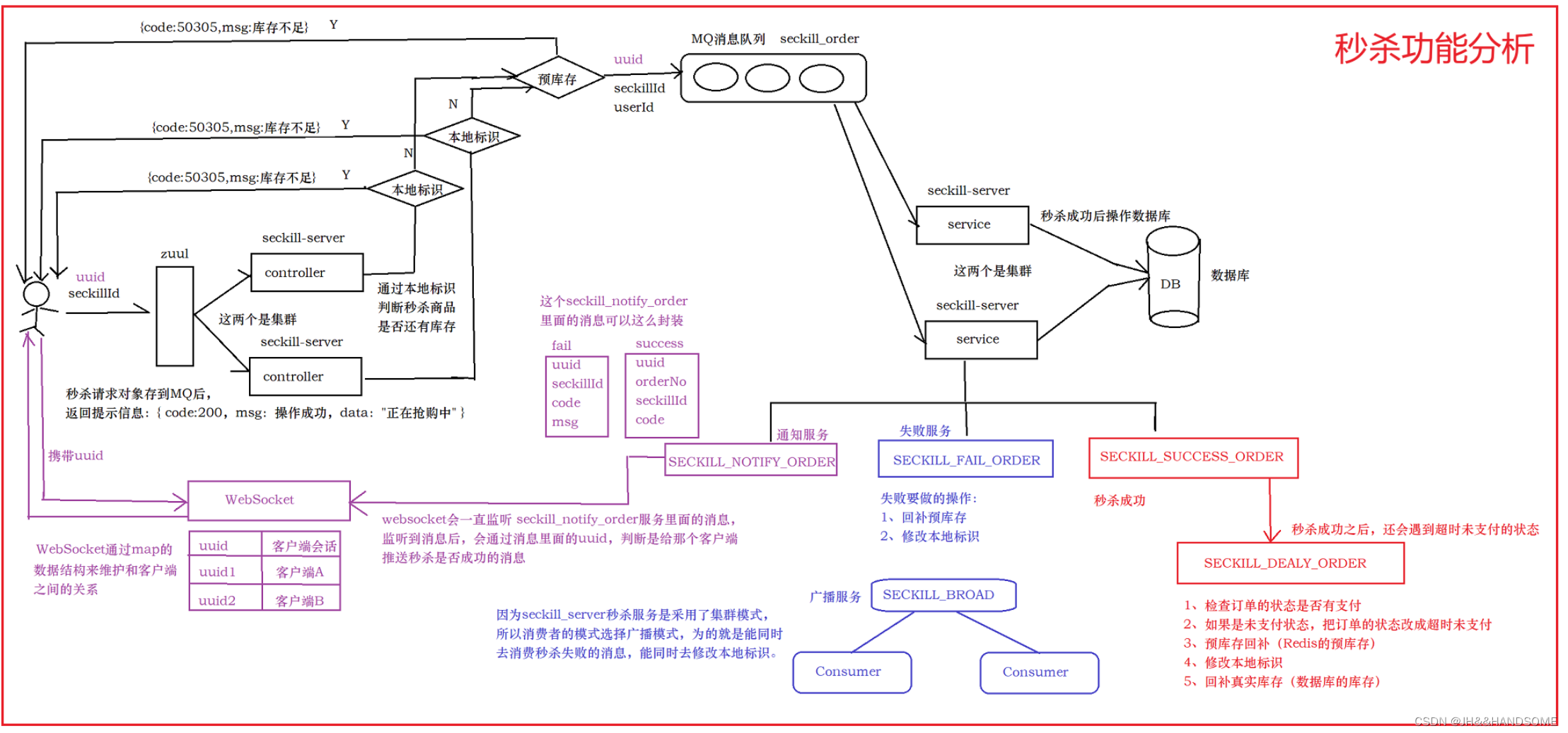
02、SpringCloud -- Redis和Cookie过期时间刷新功能
目录 需求:代码流程过滤器类工具类过滤判断远程调用feign接口gitee 配置接口实现过滤器run方法测试:问题:秒杀功能完整分析图 需求: cookie应该写在网关中,网关中可以自定义filter过滤器,用来实现cookie的刷新和redis中key的刷新,延长用户的操作时间。 就是让用户每操…...

【报错】kali安装ngrok报错解决办法(zsh: exec format error: ./ngrok)
问题描述 kali安装ngrok令牌授权失败 在安装配置文件的时候报错:zsh: exec format error: ./ngrok 原因分析: 在Kali Linux上执行./ngrok时出现zsh exec格式错误的问题可能是由于未安装正确版本的ngrok或操作系统不兼容ngrok导致的。以下是一些可能的解…...

<学习笔记>从零开始自学Python-之-常用库篇(十三)内置小型数据库shelve
一、shelve简介: shelve是Python当中数据储存的方案,类似key-value数据库,便于保存Python对象,shelve只有一个open()函数,用来打开指定的文件(字典),会返回一…...

Redis快速上手篇七(集群-六台虚拟机)
Redis集群 主从复制的场景无法吗满足主机单点故障时需要引入集群配置 一般数据库要处理的读请求远大于写请求 ,针对这种情况,我们优化数据库可以采用读写分离的策略。我们可以部 署一台主服务器主要用来处理写请求,部署多台从服务器 &#…...

LeetCode 301. 删除无效的括号【字符串,回溯或BFS】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
