LeetCode 301. 删除无效的括号【字符串,回溯或BFS】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个由若干括号和字母组成的字符串 s ,删除最小数量的无效括号,使得输入的字符串有效。
返回所有可能的结果。答案可以按 任意顺序 返回。
示例 1:
输入:s = "()())()"
输出:["(())()","()()()"]
示例 2:
输入:s = "(a)())()"
输出:["(a())()","(a)()()"]
示例 3:
输入:s = ")("
输出:[""]
提示:
1 <= s.length <= 25s由小写英文字母以及括号'('和')'组成s中至多含20个括号
有效的「括号」:题目输入的字符串由一系列「左括号」和「右括号」组成,但是有一些额外的括号,使得括号不能正确配对。对于括号配对规则如果还不太清楚的读者,可以先完成问题「20. 有效的括号」。
可以一次遍历计算出多余的「左括号」和「右括号」: 根据括号匹配规则和根据求解「[22. 括号生成]」的经验,我们知道:如果当前遍历到的「左括号」的数目严格小于「右括号」的数目则表达式无效。因此,我们可以遍历一次输入字符串,统计「左括号」和「右括号」出现的次数。
- 当遍历到「左括号」的时候:「左括号」数量加 1 1 1。
- 当遍历到「右括号」的时候:
- 如果此时「左括号」的数量不为 0 0 0,因为「右括号」可以与之前遍历到的「左括号」匹配,此时「左括号」出现的次数 − 1 -1 −1 ;
- 如果此时「左括号」的数量为 0 0 0,「右括号」数量加 1 1 1。
通过这样的计数规则,得到的「左括号」和「右括号」的数量就是各自最少应该删除的数量。
解法1 回溯+剪枝
题目让我们删除括号使得剩下的括号匹配,要求我们删除最少的括号数,并且要求得到所有的结果。我们可以使用回溯算法,尝试遍历所有可能的去掉非法括号的方案。
首先利用括号匹配的规则求出该字符串 s s s 中最少需要去掉的左括号的数目 l r e m o v e lremove lremove 和右括号的数目 r r e m o v e rremove rremove,然后我们尝试在原字符串 s s s 中去掉 l r e m o v e lremove lremove 个左括号和 r r e m o v e rremove rremove 个右括号,然后检测剩余的字符串是否合法匹配,如果合法匹配则则认为该字符串为可能的结果,我们利用回溯算法来尝试搜索所有可能的去除括号的方案。
在进行回溯时可利用以下的剪枝技巧来增加搜索的效率:
- 我们从字符串中每去掉一个括号,则更新 l r e m o v e lremove lremove 或者 r r e m o v e rremove rremove,当我们发现剩余未尝试的字符串的长度小于 l r e m o v e + r r e m o v e lremove+rremove lremove+rremove 时,则停止本次搜索。
- 当 l r e m o v e lremove lremove 和 r r e m o v e rremove rremove 同时为 0 0 0 时,则我们检测当前的字符串是否合法匹配,如果合法匹配则我们将其记录下来。
由于记录的字符串可能存在重复,因此需要对重复的结果进行去重,去重的办法有如下两种:
- 利用哈希表对最终生成的字符串去重。
- 我们在每次进行搜索时,如果遇到连续相同的括号就只需要搜索一次即可,比如当前遇到的字符串为
"(((())",去掉前四个左括号中的任意一个,生成的字符串是一样的,均为"((()),因此在尝试搜索时,只需去掉一个左括号就进行下一轮搜索,不需要将前四个左括号都尝试一遍。- 具体来说,递归搜索的第 0 0 0 层中,当前从 0 0 0 开始,删除 s [ 0 ] s[0] s[0] 的左括号,递归搜索
"((())"; - 递归搜索的第 1 1 1 层中,当前也可以从 0 0 0 开始,删除 s [ 0 ] s[0] s[0] 的左括号,递归搜索
"(())"。 - 返回到递归搜索的第 1 1 1 层,这时不会从连续左括号中进行删除,而是删除 s [ 3 ] s[3] s[3] 的右括号
- 具体来说,递归搜索的第 0 0 0 层中,当前从 0 0 0 开始,删除 s [ 0 ] s[0] s[0] 的左括号,递归搜索
根据上面的去重思路2,可以写出遍历下一个删除位置的写法:
class Solution {
public:vector<string> ans;vector<string> removeInvalidParentheses(string s) {int lremove = 0, rremove = 0; // 左括号和右括号最少应被删除的数量for (char c : s) {if (c == '(') ++lremove;else if (c == ')') {if (lremove == 0) ++rremove;else --lremove; // 左右括号匹配}}dfs(s, 0, lremove, rremove);return ans;}void dfs(const string &s, int start, int lremove, int rremove) {if (lremove == 0 && rremove == 0) {if (valid(s)) ans.push_back(s);return;}for (int i = start; i < s.size(); ++i) {if (i != start && s[i] == s[i - 1]) continue;// 如果剩余的字符无法满足去掉的数量要求,直接返回if (lremove + rremove > s.size() - i) return; // 剩余未尝试的字符串长度较小,无法继续// 尝试去掉一个左括号if (lremove > 0 && s[i] == '(')dfs(s.substr(0, i) + s.substr(i + 1), i, lremove - 1, rremove); // 注意下个开始的下标还是i// 尝试去掉一个右括号if (rremove > 0 && s[i] == ')')dfs(s.substr(0, i) + s.substr(i + 1), i, lremove, rremove - 1);}}inline bool valid(const string &s) {int cnt = 0;for (char c : s) {if (c == '(') ++cnt;else if (c == ')') { // 有括号以外的字符--cnt;if (cnt < 0) return false;}}return cnt == 0;}
};
再补充一个当前删/不删+哈希集合去重的写法,不知道该怎么去重,就用 set 存储结果:
class Solution {
public:unordered_set<string> st;vector<string> removeInvalidParentheses(string s) {int lremove = 0, rremove = 0; // 左括号和右括号最少应被删除的数量for (char c : s) {if (c == '(') ++lremove;else if (c == ')') {if (lremove == 0) ++rremove;else --lremove;}}dfs(s, 0, lremove, rremove);return vector<string>(st.begin(), st.end());}void dfs(const string &s, int i, int lremove, int rremove) {if (lremove == 0 && rremove == 0) {if (valid(s)) st.insert(s);return;}// 还需要删除的括号个数 > 能够删除的字符个数if (lremove + rremove > s.size() - i) return;// 不删除dfs(s, i + 1, lremove, rremove);// 删除,分左右括号考虑// 尝试去掉一个左括号if (lremove > 0 && s[i] == '(')dfs(s.substr(0, i) + s.substr(i + 1), i, lremove - 1, rremove);// 尝试去掉一个右括号if (rremove > 0 && s[i] == ')')dfs(s.substr(0, i) + s.substr(i + 1), i, lremove, rremove - 1);}inline bool valid(const string &s) {int cnt = 0;for (char c : s) {if (c == '(') ++cnt;else if (c == ')') { // 有括号以外的字符--cnt;if (cnt < 0) return false;}}return cnt == 0;}
};
复杂度分析:
- 时间复杂度: O ( n 2 n ) O(n2^n) O(n2n) ,其中 n n n 为字符串的长度。考虑到一个字符串最多可能有 2 n 2^n 2n 个子序列,每个子序列可能需要进行一次合法性检测,因此时间复杂度为 O ( n 2 n ) O(n2^n) O(n2n) 。
- 空间复杂度: O ( n 2 ) O(n^2) O(n2) ,其中 n n n 为字符串的长度。返回结果不计入空间复杂度,考虑到递归调用栈的深度,并且每次递归调用时需要复制字符串一次,因此空间复杂度为 O ( n 2 ) O(n^2) O(n2) 。
解法2 广度优先搜索
注意到题目中要求最少删除,这样的描述正是广度优先搜索算法应用的场景,并且题目也要求我们输出所有的结果。我们在进行广度优先搜索时每一轮删除字符串中的 1 1 1 个括号,直到出现合法匹配的字符串为止,此时进行轮转的次数即为最少需要删除括号的个数。
我们进行广度优先搜索时,每次保存上一轮搜索的结果,然后对「上一轮已经保存的结果中的每个字符串」尝试所有可能的删除一个括号的方法,然后将保存的结果进行下一轮搜索。在保存结果时,我们可以利用哈希表对上一轮生成的结果去重,从而提高效率。
class Solution {
public:unordered_set<string> curSet;vector<string> removeInvalidParentheses(string s) {vector<string> ans;curSet.insert(s);while (true) {for (auto &str : curSet) if (valid(str)) ans.emplace_back(str);if (ans.size() > 0) return ans; // BFS,删除括号最少的合法字符串unordered_set<string> nextSet;for (auto &str : curSet) {for (int i = 0; i < str.size(); ++i) {if (i > 0 && str[i] == str[i - 1]) continue; // 对当前连续重复的括号只需删除一个if (str[i] == '(' || str[i] == ')') // 第k步迭代,删除第k个括号nextSet.insert(str.substr(0, i) + str.substr(i + 1, str.size()));}}curSet = nextSet;}}inline bool valid(const string &s) {int cnt = 0;for (char c : s) {if (c == '(') ++cnt;else if (c == ')') { // 有括号以外的字符--cnt;if (cnt < 0) return false;}}return cnt == 0;}
};
复杂度分析:
- 时间复杂度: O ( n 2 n ) O(n2^n) O(n2n) ,其中 n n n 为字符串的长度。考虑到一个字符串最多可能有 2 n 2^n 2n 个子序列,因此时间复杂度为 O ( n 2 n ) O(n2^n) O(n2n) 。
- 空间复杂度: O ( n × C n n 2 ) O(n \times C_n^\frac{n}{2}) O(n×Cn2n) ,其中 n n n 为字符串的长度。我们在进行第 i i i 轮迭代时,会从原始字符串中删除 i i i 个括号,因此第 i i i 轮迭代产生的字符串最多有 C n i C_n^i Cni 个,当 i = n 2 i = \frac{n}{2} i=2n 时组合数最大,此时迭代生成的字符串个数最多,因此空间复杂度为 O ( n × C n n 2 ) O(n \times C_n^\frac{n}{2}) O(n×Cn2n) 。
解法3 枚举状态子集
首先我们利用括号匹配的规则,求出该字符串 s s s 中最少需要去掉的左括号的数目 l r e m o v e lremove lremove 和右括号的数目 r r e m o v e rremove rremove,然后我们利用状态子集,求出字符串 s s s 中所有的左括号去掉 l r e m o v e lremove lremove 的左括号的子集,和所有的右括号去掉 r r e m o v e rremove rremove 个右括号的子集,依次枚举这两种子集的组合,检测组合后的字符串是否合法匹配,如果字符串合法则记录,最后我们利用哈希表对结果进行去重。
class Solution {
public:bool checkValid(const string & str, int lmask, vector<int> & left, int rmask, vector<int> & right) {int pos1 = 0;int pos2 = 0;int cnt = 0;for (int i = 0; i < str.size(); i++) {if (pos1 < left.size() && i == left[pos1]) {if (!(lmask & (1 << pos1))) {cnt++;}pos1++;} else if (pos2 < right.size() && i == right[pos2]) {if (!(rmask & (1 << pos2))) {cnt--;if (cnt < 0) {return false;}}pos2++;}}return cnt == 0;}string recoverStr(const string & str, int lmask, vector<int> & left, int rmask, vector<int> & right){string ans;int pos1 = 0;int pos2 = 0;for (int i = 0; i < str.size(); i++) {if (pos1 < left.size() && i == left[pos1]) {if (!(lmask & (1 << pos1))){ans.push_back(str[i]);}pos1++;} else if (pos2 < right.size() && i == right[pos2]) {if (!(rmask & (1 << pos2))) {ans.push_back(str[i]);}pos2++;} else {ans.push_back(str[i]);}}return ans;}vector<string> removeInvalidParentheses(string s) {int lremove = 0;int rremove = 0;vector<int> left;vector<int> right;vector<string> ans;unordered_set<string> cnt;for (int i = 0; i < s.size(); i++) {if (s[i] == '(') {left.push_back(i);lremove++;} else if (s[i] == ')') {right.push_back(i);if (lremove == 0) {rremove++;} else {lremove--;}}}int m = left.size();int n = right.size();vector<int> maskArr1;vector<int> maskArr2;for (int i = 0; i < (1 << m); i++) {if (__builtin_popcount(i) != lremove) {continue;}maskArr1.push_back(i);}for (int j = 0; j < (1 << n); j++) {if (__builtin_popcount(j) != rremove) {continue;}maskArr2.push_back(j);}for (auto mask1 : maskArr1) {for (auto mask2 : maskArr2) {if (checkValid(s, mask1, left, mask2, right)) {cnt.insert(recoverStr(s, mask1, left, mask2, right));}}}for (auto v : cnt) {ans.emplace_back(v);}return ans;}
};
复杂度分析:
- 时间复杂度: O ( n 2 n ) O(n2^n) O(n2n) ,其中 n n n 为字符串的长度。考虑到一个字符串最多可能有 2 n 2^n 2n 个子序列,每个子序列可能需要进行一次合法性检测,因此时间复杂度为 O ( n 2 n ) O(n2^n) O(n2n) 。
- 空间复杂度: O ( n × C n m ) O(n \times C_n^m) O(n×Cnm) ,其中 n n n 为字符串的长度, m m m 为字符串中非法括号的数目。空间复杂度主要为集合 cnt \texttt{cnt} cnt 占用的空间。
相关文章:

LeetCode 301. 删除无效的括号【字符串,回溯或BFS】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

面试经典159题——Day25
文章目录 一、题目二、题解 一、题目 125. Valid Palindrome A phrase is a palindrome if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric charact…...
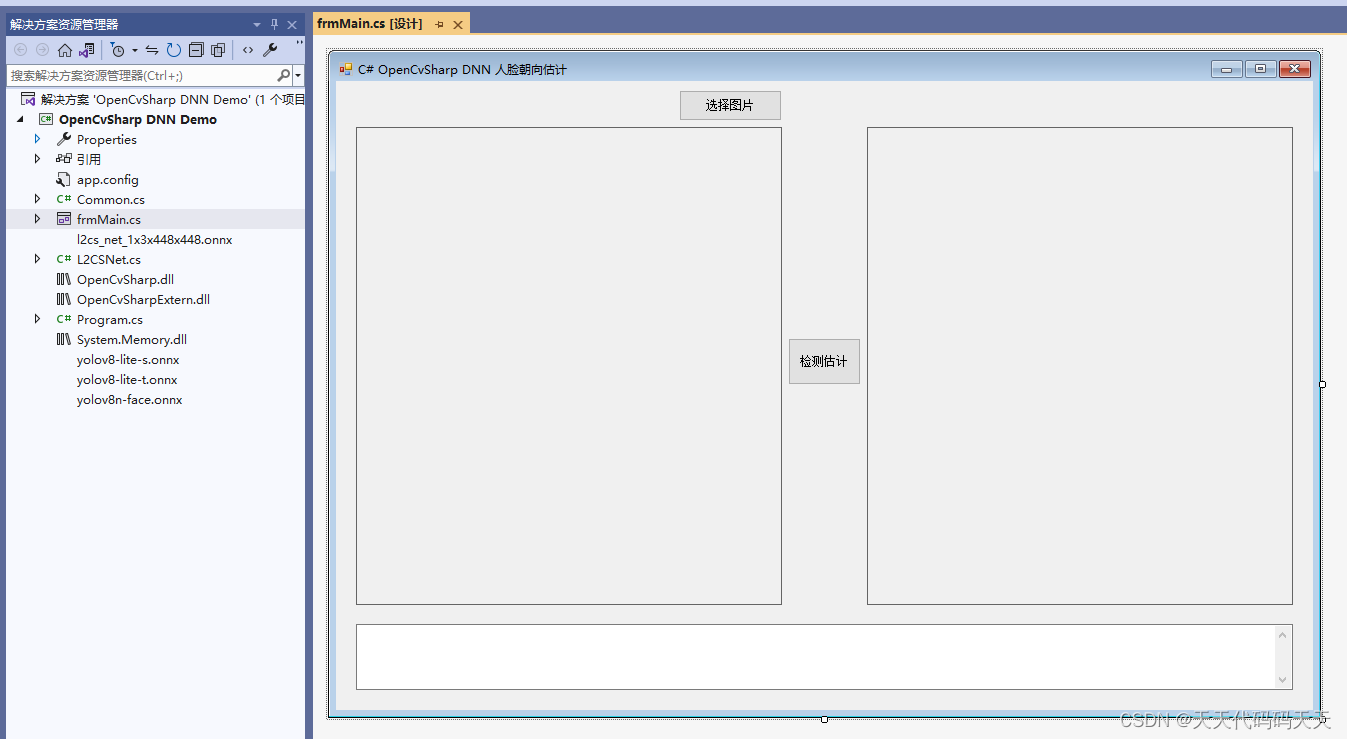
C# OpenCvSharp DNN 部署L2CS-Net人脸朝向估计
效果 项目 代码 using OpenCvSharp; using OpenCvSharp.Dnn; using System; using System.Collections.Generic; using System.Drawing; using System.Drawing.Drawing2D; using System.Linq; using System.Text; using System.Windows.Forms;namespace OpenCvSharp_DNN_Demo …...
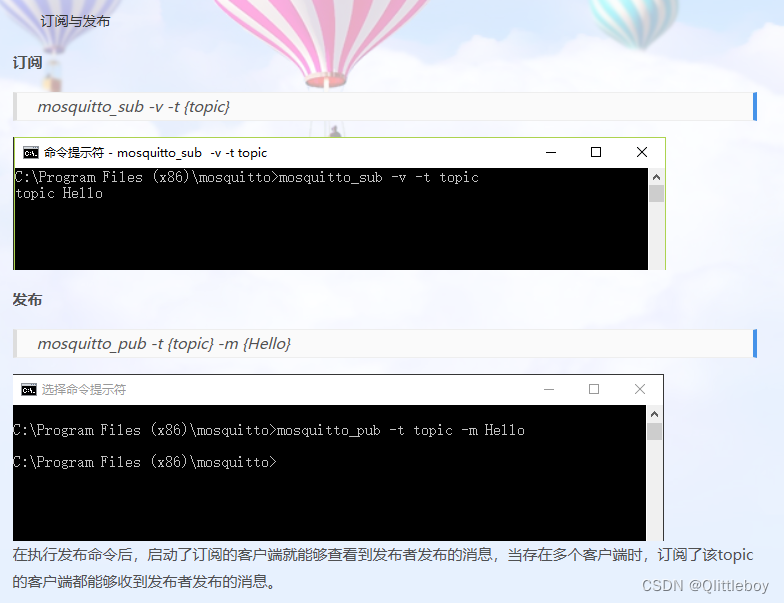
Windows环境下MosQuitto服务器搭建,安装mqtt服务端软件
1、下载、安装MosQuitto服务器 下载地址:http://mosquitto.org/files/binary/ 根据平台选择相应的代码下载。 安装完成后,安装文件夹下部分文件的功能...
web前端JS基础-----制作进度条
1,参考代码 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title></head><body><progress id"pro" max"100" value"0"></progress><scrip…...

Linux命令解压多个tar.gz包
命令行解压单个tar.gz包: tar zxvf package.tar.gz 命令行解压多个tar.gz包: for f in *.tar.gz; do tar zxvf "$f"; done 这个命令会循环遍历当前目录下的所有tar.gz包,然后逐个解压。 注:如果想要解压到指定的目…...

Java基于SpringBoot+Vue的网上图书商城管理系统(附源码,教程)
文章目录 1. 简介2 技术栈3 系统功能4系统设计4.1数据库设计 5系统详细设计5.1系统功能模块5.1系统功能模块5.2管理员功能模块 源码下载地址 1. 简介 本次设计任务是要设计一个网上图书商城,通过这个系统能够满足网上图书商城的管理功能。系统的主要功能包括首页、…...
Visual Studio Code的下载与安装
Visual Studio Code(简称 VS Code)是由 Microsoft 开发的免费、开源的文本编辑器,适用于多种操作系统,包括 Windows、macOS 和 Linux。它的设计目标是成为一款轻量级、高效的代码编辑工具,同时提供丰富的扩展和功能&am…...

23种设计模式在SpringCloud源码里的应用
单例模式(Singleton):Spring 中的 Bean 默认都是单例模式,保证在整个应用中只有一个实例。 工厂方法模式(Factory Method):Spring 中的 BeanFactory 和 ApplicationContext 都实现了工厂方法模…...

几个精致的Linux命令
说到Linux命令,一些基础的简单的单个命令我就不说了,咱今天来点复杂的组合命令,比较长,但觉对很酷: 打印业务服务异常日志: tail -f business-service.log | grep -i exception --color 或者 grep --…...
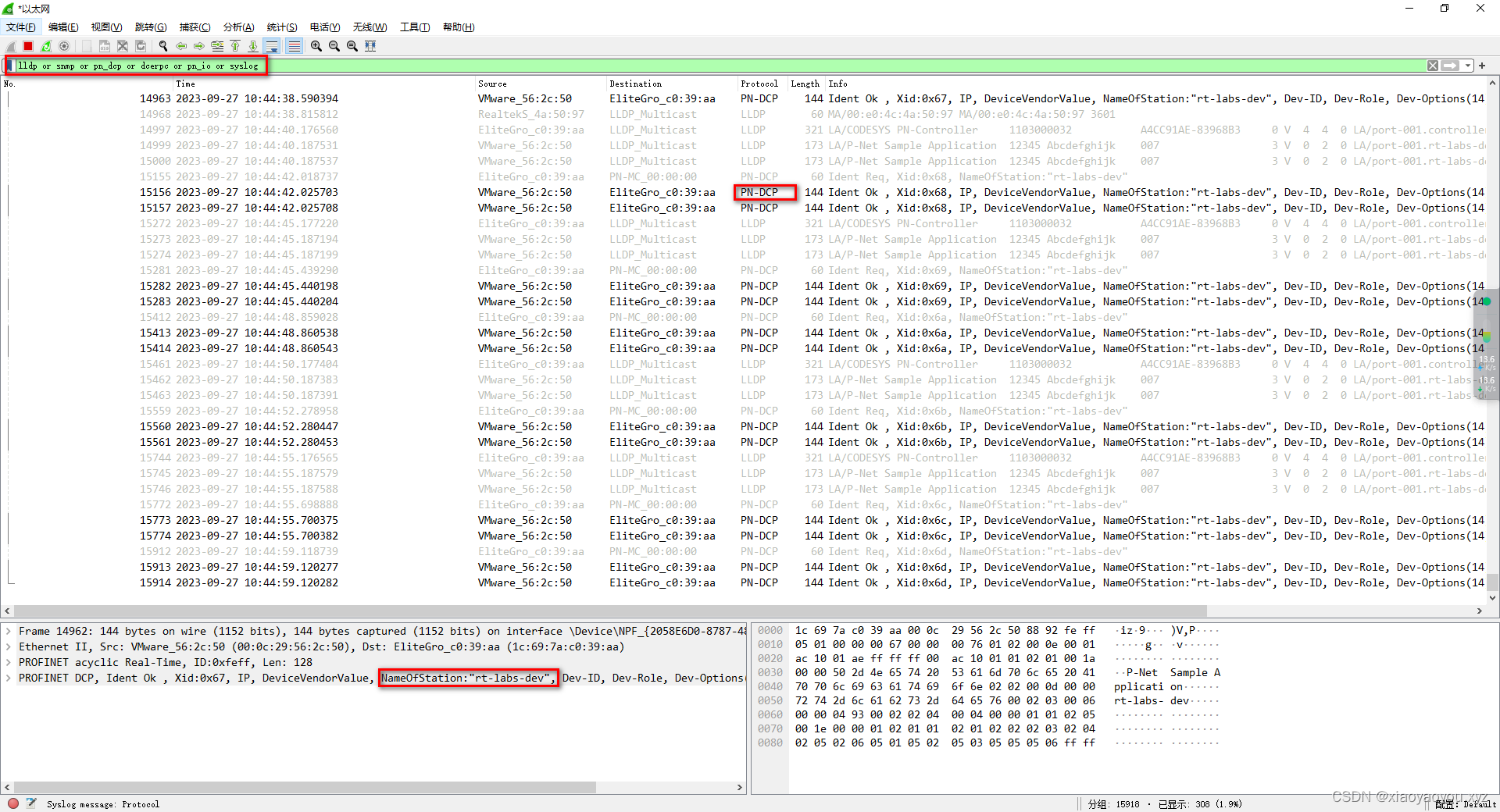
CoDeSys系列-3、Windows运行时软PLC主站和p-net从站IO设备组网测试
CoDeSys系列-3、Windows运行时软PLC主站和p-net从站IO设备组网测试 文章目录 CoDeSys系列-3、Windows运行时软PLC主站和p-net从站IO设备组网测试一、前言二、Windows运行时软plc配置编程1、安装Windows下的运行时扩展包(非必要)2、创建项目2.1、创建标准…...
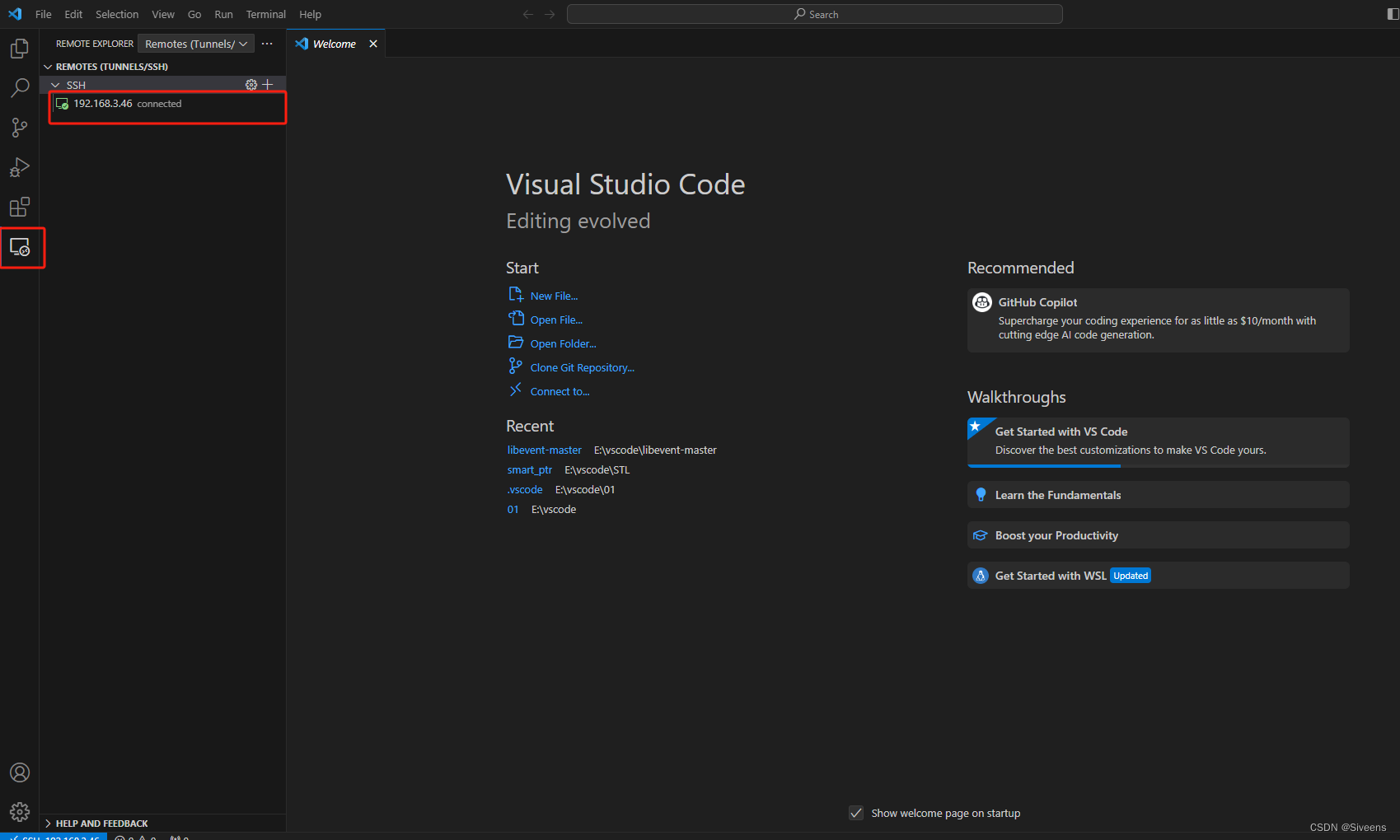
vscode下ssh免密登录linux服务器
vscode使用ssh免密登录linux 1、安装SSH插件2、生成密钥3、linux安装ssh服务4、linux下配置公钥5、vscode远程登录 注:测试环境为window10Ubuntu1804/Ubuntu2204 1、安装SSH插件 扩展->搜索SSH->点击install进行安装,如下图所示: 2、…...

基于jquery+html开发的json格式校验工具
json简介 JSON是一种轻量级的数据交换格式。 易于人阅读和编写。同时也易于机器解析和生成。 它基于JavaScript Programming Language, Standard ECMA-262 3rd Edition - December 1999的一个子集。 JSON采用完全独立于语言的文本格式,但是也使用了类似于C语言家族…...

【面试经典150 | 栈】最小栈
文章目录 Tag题目来源题目解读解题思路方法一:辅助栈方法二:一个栈方法三:栈中存放差值 其他语言python3 写在最后 Tag 【设计类】【栈】 题目来源 155. 最小栈 题目解读 本题是一个设计类的题目,设计一个最小栈类 MinStack() …...
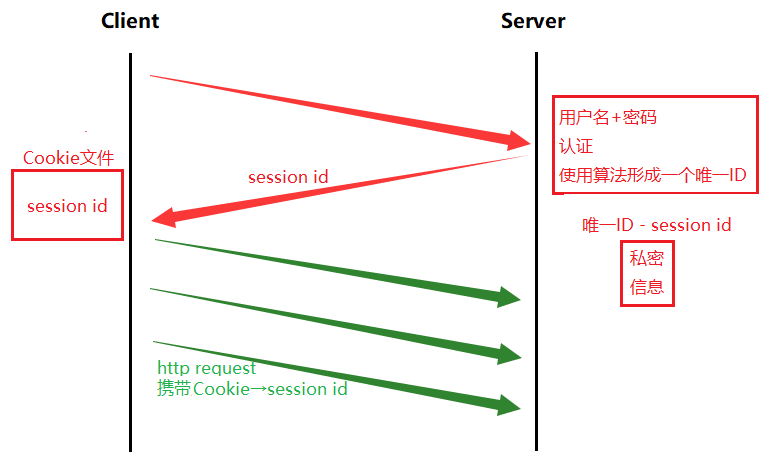
Linux网络基础2 -- 应用层相关
一、协议 引例:编写一个网络版的计算器 1.1 约定方案:“序列化” 和 “反序列化” 方案一:客户端发送形如“11”的字符串,再去解析其中的数字和计算字符,并且设限(如数字和运算符之间没有空格; 运算符只…...

【Python机器学习】零基础掌握SkewedChi2Sampler内核近似特征
有没有遇到这样的困扰:即使在拥有大量数据的条件下,传统的机器学习模型表现依然不佳?这时,数据预处理和特征工程成了解决问题的关键步骤。那么,有没有一种算法能够优化特征,提升模型性能呢? 假设一个在线商城希望通过用户行为(比如点击、购买等)来预测用户是否会成为…...
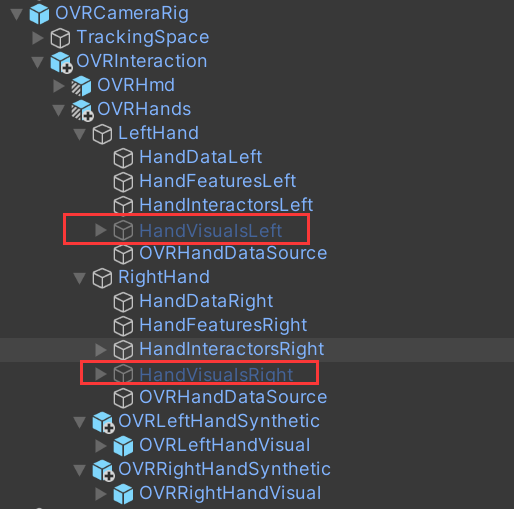
Unity Meta Quest 一体机开发(三):Oculus Integration 基本原理、概念与结构+玩家角色基本配置
文章目录 📕教程说明📕输入数据📕Oculus Integration 处理手部数据的推荐流程📕VR 中交互的基本概念📕Oculus Integration 中的交互流程📕配置一个基本的玩家物体⭐OVRCameraRig⭐OVRInteraction⭐OVRHandP…...

excel 拼接字符 单元格
需要将单元格作为字符串拼接,使用 & 符号,拼接逗号,分号,冒号,横杠等,需要用英文双引号。...
HarmonyOS 快速入门TypeScript
1.什么是TypeScript,它和JavaScript,ArkTs有什么区别 ArkTS是HarmonyOS优选的主力应用开发语言。它在TypeScript(简称TS)的基础上,匹配ArkUI框架,扩展了声明式UI、状态管理等相应的能力,让开发…...
ChatGPT扩展系列之ChatExcel
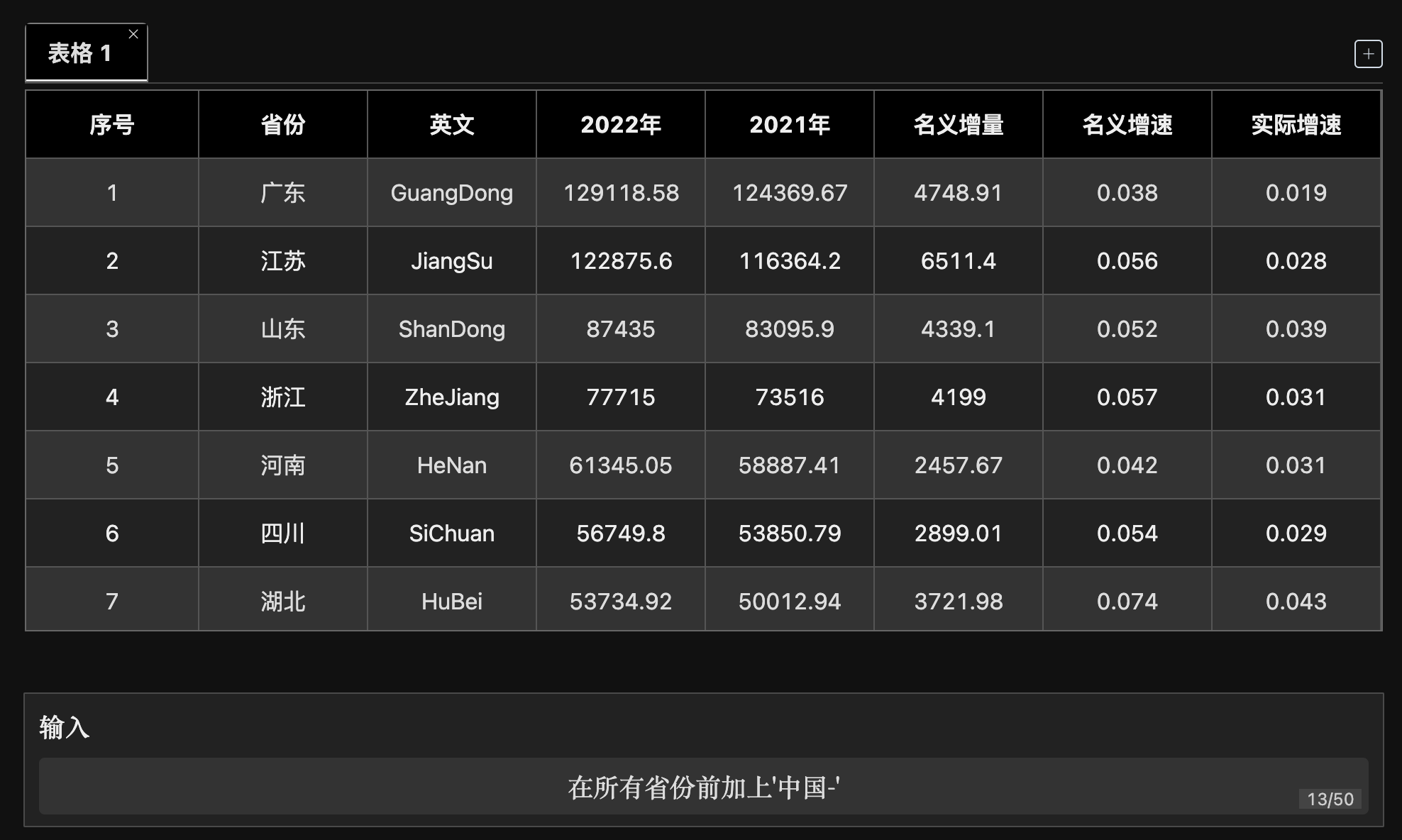
文章目录 ChatGPT扩展系列之ChatExcel对某一列的文字进行处理对数据进行排序对数据进行计算微软官方又推出Excel AI插件ChatGPT扩展系列之ChatExcel 自从ChatGPT很空出世之后,很多基于ChatGPT的应用便如雨后春笋般应用而生,这些应用的底层本质就是利用了ChatGPT对自然语言的…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
