【机器学习】loss损失讨论
大纲
- 验证集loss上升,准确率也上升(即将overfitting?)
- 训练集loss一定为要为0吗
Q1. 验证集loss上升,准确率也上升
随着置信度的增加,一小部分点的预测结果是错误的(log lik 给出了指数级的惩罚,在损失中占主导地位)。与此同时,大量其他点开始预测良好(argmax p=label),主导了预测的准确性。
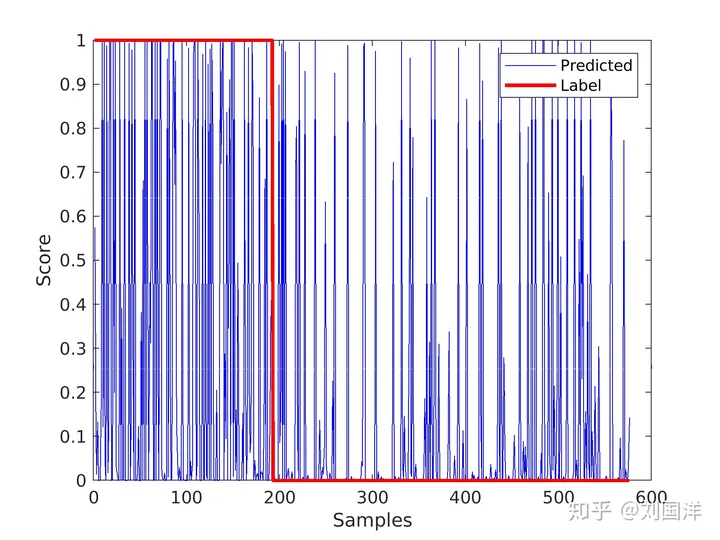
Q2. 训练集loss一定为要为0吗
一般来说,我们是用训练集来训练模型,但希望的是验证机的损失越小越好,而正常来说训练集的损失降到一定值后,验证集的损失就会开始上升,因此没必要把训练集的损失降低到 0
既然如此,在已经达到了某个阈值之后,我们可不可以做点别的事情来提升模型性能呢?ICML2020 的论文《Do We Need Zero Training Loss After Achieving Zero Training Error?》回答了这个问题,不过实际上它并没有很好的描述 “为什么”,而只是提出了 “怎么做”
假设原来的损失函数是 L ( θ ) \mathcal {L}(\theta) L(θ),现在改为 L ~ ( θ ) \tilde {\mathcal {L}}(\theta) L~(θ):
L ~ ( θ ) = ∣ L ( θ ) − b ∣ + b (1) \tilde{\mathcal{L}}(\theta)=|\mathcal{L}(\theta)-b|+b\tag{1} L~(θ)=∣L(θ)−b∣+b(1)
其中 b b b 是预先设定的阈值。当 L ( θ ) > b \mathcal {L}(\theta)>b L(θ)>b 时 L ~ ( θ ) = L ( θ ) \tilde {\mathcal {L}}(\theta)=\mathcal {L}(\theta) L~(θ)=L(θ),这时就是执行普通的梯度下降;而 L ( θ ) < b \mathcal {L}(\theta)<b L(θ)<b 时 L ~ ( θ ) = 2 b − L ( θ ) \tilde {\mathcal {L}}(\theta)=2b-\mathcal {L}(\theta) L~(θ)=2b−L(θ),注意到损失函数变号了,所以这时候是梯度上升。因此,总的来说就是以 b b b 为阈值,低于阈值时反而希望损失函数变大。论文把这个改动称为 “Flooding”
这样做有什么效果呢?论文显示,在某些任务中,训练集的损失函数经过这样处理后,验证集的损失能出现 “二次下降(Double Descent)”,如下图
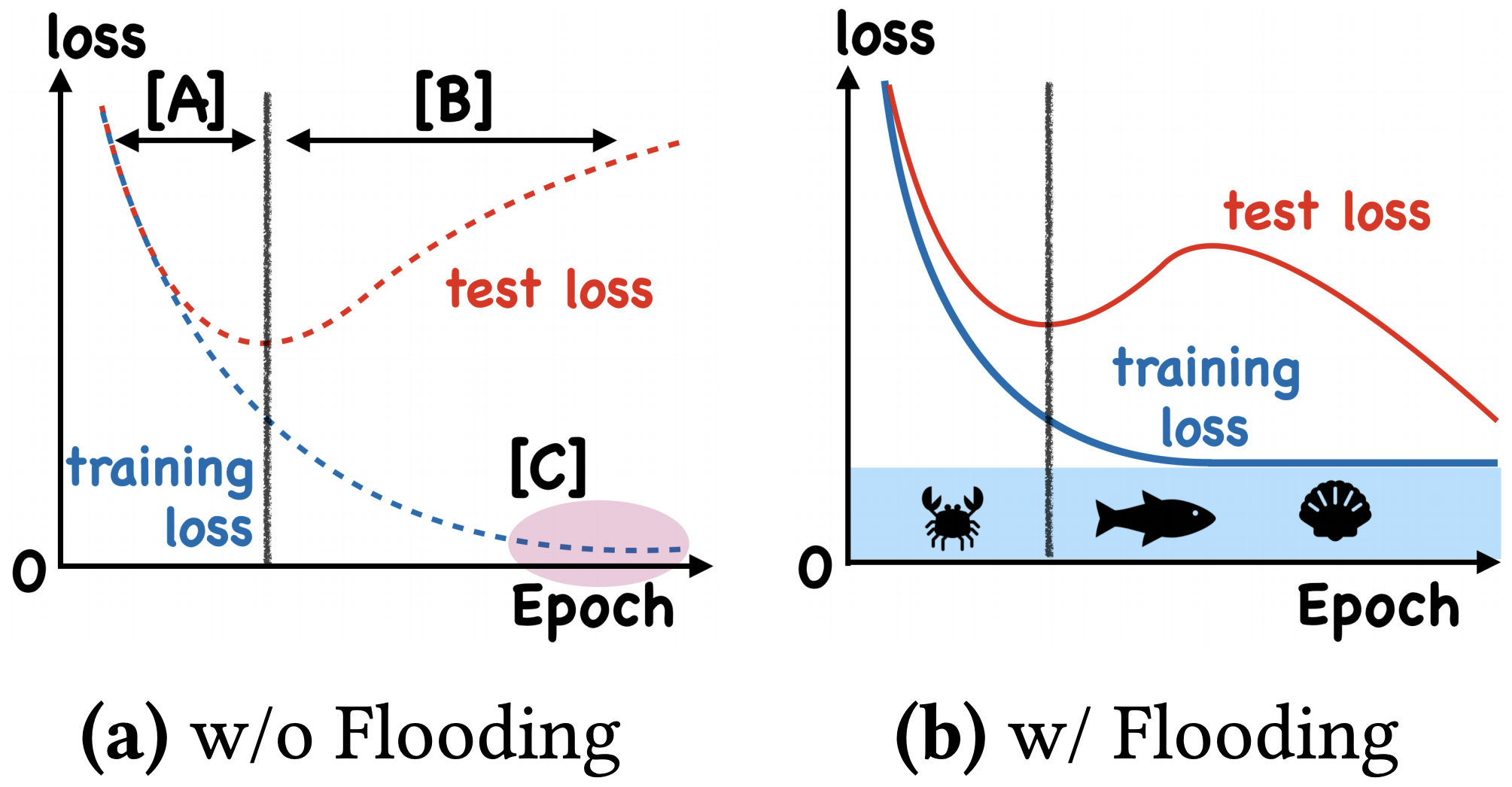
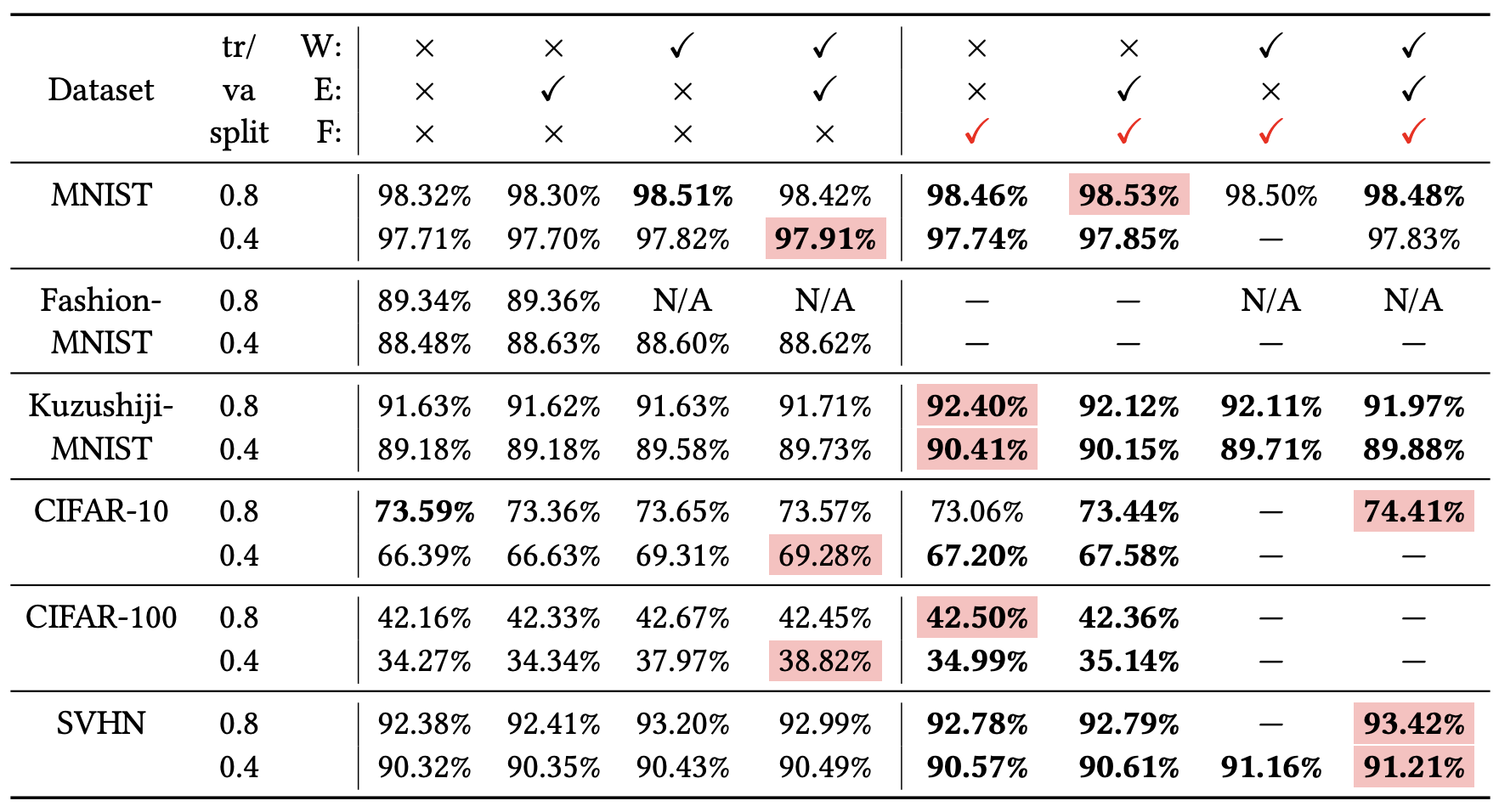
如何解释这个方法呢?可以想像,当损失函数达到 b b b 之后,训练流程大概就是在交替执行梯度下降和梯度上升。直观想的话,感觉一步上升一步下降,似乎刚好抵消了。事实真的如此吗?我们来算一下看看。假设先下降一步后上升一步,学习率为 ε \varepsilon ε,那么:
θ n = θ n − 1 − ε g ( θ n − 1 ) θ n + 1 = θ n + ε g ( θ n ) \begin{equation}\begin{aligned}&\theta_n = \theta_{n-1} - \varepsilon g(\theta_{n-1})\\ &\theta_{n+1} = \theta_n + \varepsilon g(\theta_n) \end{aligned}\tag{2}\end{equation} θn=θn−1−εg(θn−1)θn+1=θn+εg(θn)(2)
其中 g ( θ ) = ∇ θ L ( θ ) g (\theta)=\nabla_{\theta}\mathcal {L}(\theta) g(θ)=∇θL(θ),现在我们有
θ n + 1 = θ n − 1 − ε g ( θ n − 1 ) + ε g ( θ n − 1 − ε g ( θ n − 1 ) ) ≈ θ n − 1 − ε g ( θ n − 1 ) + ε ( g ( θ n − 1 ) − ε ∇ θ g ( θ n − 1 ) g ( θ n − 1 ) ) = θ n − 1 − ε 2 2 ∇ θ ∥ g ( θ n − 1 ) ∥ 2 \begin{equation}\begin{aligned}\theta_{n+1} =&\, \theta_{n-1} - \varepsilon g(\theta_{n-1}) + \varepsilon g\big(\theta_{n-1} - \varepsilon g(\theta_{n-1})\big)\\ \approx&\,\theta_{n-1} - \varepsilon g(\theta_{n-1}) + \varepsilon \big(g(\theta_{n-1}) - \varepsilon \nabla_{\theta} g(\theta_{n-1}) g(\theta_{n-1})\big)\\ =&\,\theta_{n-1} - \frac{\varepsilon^2}{2}\nabla_{\theta}\Vert g(\theta_{n-1})\Vert^2 \end{aligned}\tag{3}\end{equation} θn+1=≈=θn−1−εg(θn−1)+εg(θn−1−εg(θn−1))θn−1−εg(θn−1)+ε(g(θn−1)−ε∇θg(θn−1)g(θn−1))θn−1−2ε2∇θ∥g(θn−1)∥2(3)
近似那一步实际上是使用了泰勒展开,我们将 θ n − 1 \theta_{n-1} θn−1 看作 x x x, ε g ( θ n − 1 ) \varepsilon g (\theta_{n-1}) εg(θn−1) 看作 Δ x \Delta x Δx,由于
g ( x − Δ x ) − g ( x ) − Δ x = ∇ x g ( x ) \frac{g(x - \Delta x) - g(x)}{-\Delta x} = \nabla_x g(x) −Δxg(x−Δx)−g(x)=∇xg(x) 所以
g ( x − Δ x ) = g ( x ) − Δ x ∇ x g ( x ) g(x - \Delta x) = g(x) - \Delta x \nabla_x g(x) g(x−Δx)=g(x)−Δx∇xg(x)
最终的结果就是相当于学习率为 ε 2 2 \frac {\varepsilon^2}{2} 2ε2、损失函数为梯度惩罚 ∥ g ( θ ) ∥ 2 = ∥ ∇ θ L ( θ ) ∥ 2 \Vert g (\theta)\Vert^2 = \Vert \nabla_{\theta} \mathcal {L}(\theta)\Vert^2 ∥g(θ)∥2=∥∇θL(θ)∥2 的梯度下降。更妙的是,改为 “先上升再下降”,其表达式依然是一样的(这不禁让我想起 “先涨价 10% 再降价 10%” 和 “先降价 10% 再涨价 10% 的故事”)。因此,平均而言,Flooding 对损失函数的改动,相当于在保证了损失函数足够小之后去最小化 ∥ ∇ x L ( θ ) ∥ 2 \Vert \nabla_x \mathcal {L}(\theta)\Vert^2 ∥∇xL(θ)∥2,也就是推动参数往更平稳的区域走,这通常能提高泛化性(更好地抵抗扰动),因此一定程度上就能解释 Flooding 有作用的原因了
本质上来讲,这跟往参数里边加入随机扰动、对抗训练等也没什么差别,只不过这里是保证了损失足够小后再加扰动
想要使用 Flooding 非常简单,只需要在原有代码基础上增加一行即可
logits = model(x)
loss = criterion(logits, y)
loss = (loss - b).abs() + b # This is it!
optimizer.zero_grad()
loss.backward()
optimizer.step()
有心是用这个方法的读者可能会纠结于 b b b 的选择,原论文说 b b b 的选择是一个暴力迭代的过程,需要多次尝试
The flood level is chosen from b ∈ { 0 , 0.01 , 0.02 , . . . , 0.50 } b\in \{0, 0.01,0.02,...,0.50\} b∈{0,0.01,0.02,...,0.50}
不过笔者倒是有另外一个脑洞: b b b 无非就是决定什么时候开始交替训练罢了,那如果我们从一开始就用不同的学习率进行交替训练呢?也就是自始自终都执行
θ n = θ n − 1 − ε 1 g ( θ n − 1 ) θ n + 1 = θ n + ε 2 g ( θ n ) \begin{equation}\begin{aligned}&\theta_n = \theta_{n-1} - \varepsilon_1 g(\theta_{n-1})\\ &\theta_{n+1} = \theta_n + \varepsilon_2 g(\theta_n) \end{aligned}\tag{4}\end{equation} θn=θn−1−ε1g(θn−1)θn+1=θn+ε2g(θn)(4)
其中 ε 1 > ε 2 \varepsilon_1 > \varepsilon_2 ε1>ε2,这样我们就把 b b b 去掉了(引入了 ε 1 , ε 2 \varepsilon_1, \varepsilon_2 ε1,ε2 的选择,天下没有免费的午餐)。重复上述近似展开,我们就得到
θ n + 1 = θ n − 1 − ε 1 g ( θ n − 1 ) + ε 2 g ( θ n − 1 − ε 1 g ( θ n − 1 ) ) ≈ θ n − 1 − ε 1 g ( θ n − 1 ) + ε 2 ( g ( θ n − 1 ) − ε 1 ∇ θ g ( θ n − 1 ) g ( θ n − 1 ) ) = θ n − 1 − ( ε 1 − ε 2 ) g ( θ n − 1 ) − ε 1 ε 2 2 ∇ θ ∥ g ( θ n − 1 ) ∥ 2 = θ n − 1 − ( ε 1 − ε 2 ) ∇ θ [ L ( θ n − 1 ) + ε 1 ε 2 2 ( ε 1 − ε 2 ) ∥ ∇ θ L ( θ n − 1 ) ∥ 2 ] \begin{equation}\begin{aligned} \theta_{n+1} =& \, \theta_{n-1} - \varepsilon_1g(\theta_{n-1})+\varepsilon_2g(\theta_{n-1} - \varepsilon_1g(\theta_{n-1}))\\ \approx&\, \theta_{n-1} - \varepsilon_1g(\theta_{n-1}) + \varepsilon_2(g(\theta_{n-1}) - \varepsilon_1\nabla_\theta g(\theta_{n-1})g(\theta_{n-1}))\\ =&\, \theta_{n-1} - (\varepsilon_1 - \varepsilon_2) g(\theta_{n-1}) - \frac{\varepsilon_1\varepsilon_2}{2}\nabla_{\theta}\Vert g(\theta_{n-1})\Vert^2\\ =&\,\theta_{n-1} - (\varepsilon_1 - \varepsilon_2)\nabla_{\theta}\left[\mathcal{L}(\theta_{n-1}) + \frac{\varepsilon_1\varepsilon_2}{2(\varepsilon_1 - \varepsilon_2)}\Vert \nabla_{\theta}\mathcal{L}(\theta_{n-1})\Vert^2\right] \end{aligned}\tag{5}\end{equation} θn+1=≈==θn−1−ε1g(θn−1)+ε2g(θn−1−ε1g(θn−1))θn−1−ε1g(θn−1)+ε2(g(θn−1)−ε1∇θg(θn−1)g(θn−1))θn−1−(ε1−ε2)g(θn−1)−2ε1ε2∇θ∥g(θn−1)∥2θn−1−(ε1−ε2)∇θ[L(θn−1)+2(ε1−ε2)ε1ε2∥∇θL(θn−1)∥2](5)
这就相当于自始自终都在用学习率 ε 1 − ε 2 \varepsilon_1-\varepsilon_2 ε1−ε2 来优化损失函数 L ( θ ) + ε 1 ε 2 2 ( ε 1 − ε 2 ) ∥ ∇ θ L ( θ ) ∥ 2 \mathcal {L}(\theta) + \frac {\varepsilon_1\varepsilon_2}{2 (\varepsilon_1 - \varepsilon_2)}\Vert\nabla_{\theta}\mathcal {L}(\theta)\Vert^2 L(θ)+2(ε1−ε2)ε1ε2∥∇θL(θ)∥2 了,也就是说一开始就把梯度惩罚给加了进去,这样能提升模型的泛化性能吗?《Backstitch: Counteracting Finite-sample Bias via Negative Steps》里边指出这种做法在语音识别上是有效的,请读者自行测试甄别
效果检验
我随便在网上找了个竞赛,然后利用别人提供的以 BERT 为 baseline 的代码,对 Flooding 的效果进行了测试,下图分别是没有做 Flooding 和参数 b = 0.7 b=0.7 b=0.7 的 Flooding 损失值变化图,值得一提的是,没有做 Flooding 的验证集最低损失值为 0.814198,而做了 Flooding 的验证集最低损失值为 0.809810
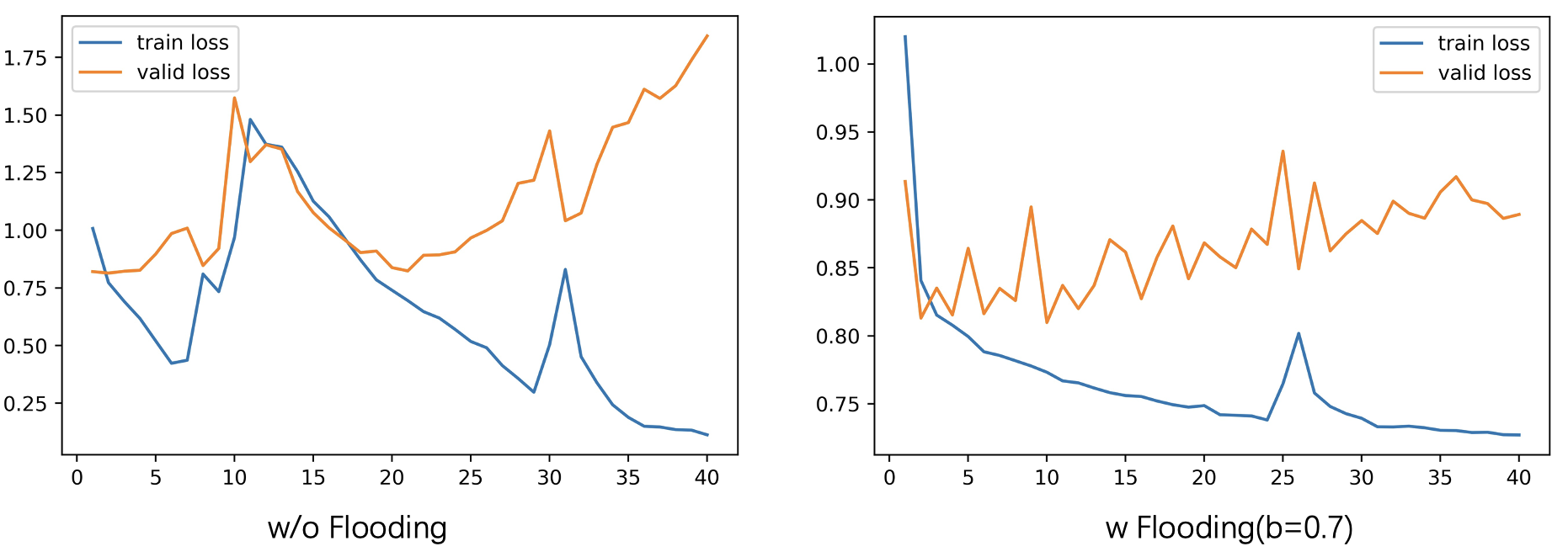
根据知乎文章一行代码发一篇 ICML?底下用户 Curry 评论所言:“通常来说 b b b 值需要设置成比 'Validation Error 开始上升 ’ 的值更小,1/2 处甚至更小,结果更优”,所以我仔细观察了下没有加 Flooding 模型损失值变化图,大概在 loss 为 0.75 到 1.0 左右的时候开始出现过拟合现象,因此我又分别设置了 b = 0.4 b=0.4 b=0.4 和 b = 0.5 b=0.5 b=0.5,做了两次 Flooding 实验,结果如下图
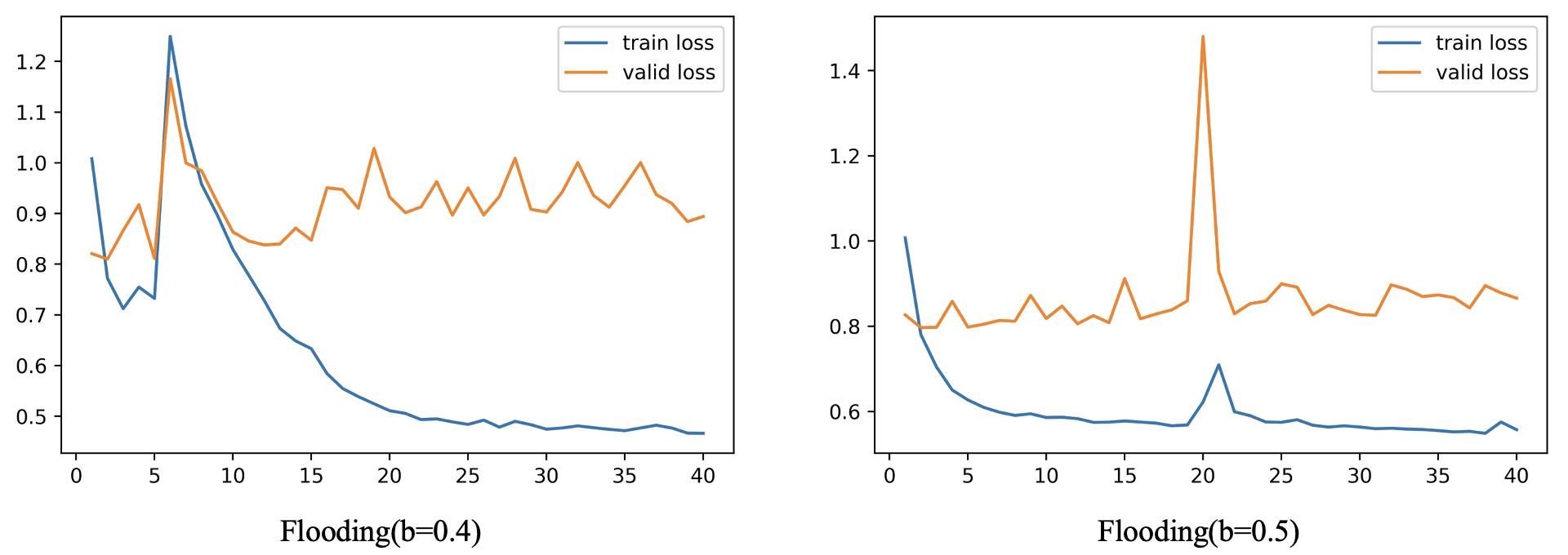
值得一提的是, b = 0.4 b=0.4 b=0.4 和 b = 0.5 b=0.5 b=0.5 时,验证集上的损失值最低仅为 0.809958 和 0.796819,而且很明显验证集损失的整体上升趋势更加缓慢。接下来我做了一个实验,主要是验证 “继续脑洞” 部分以不同的学习率一开始就交替着做梯度下降和梯度上升的效果,其中,梯度下降的学习率我设为 1 e − 5 1e-5 1e−5,梯度上升的学习率为 1 e − 6 1e-6 1e−6,结果如下图,验证集的损失最低仅有 0.783370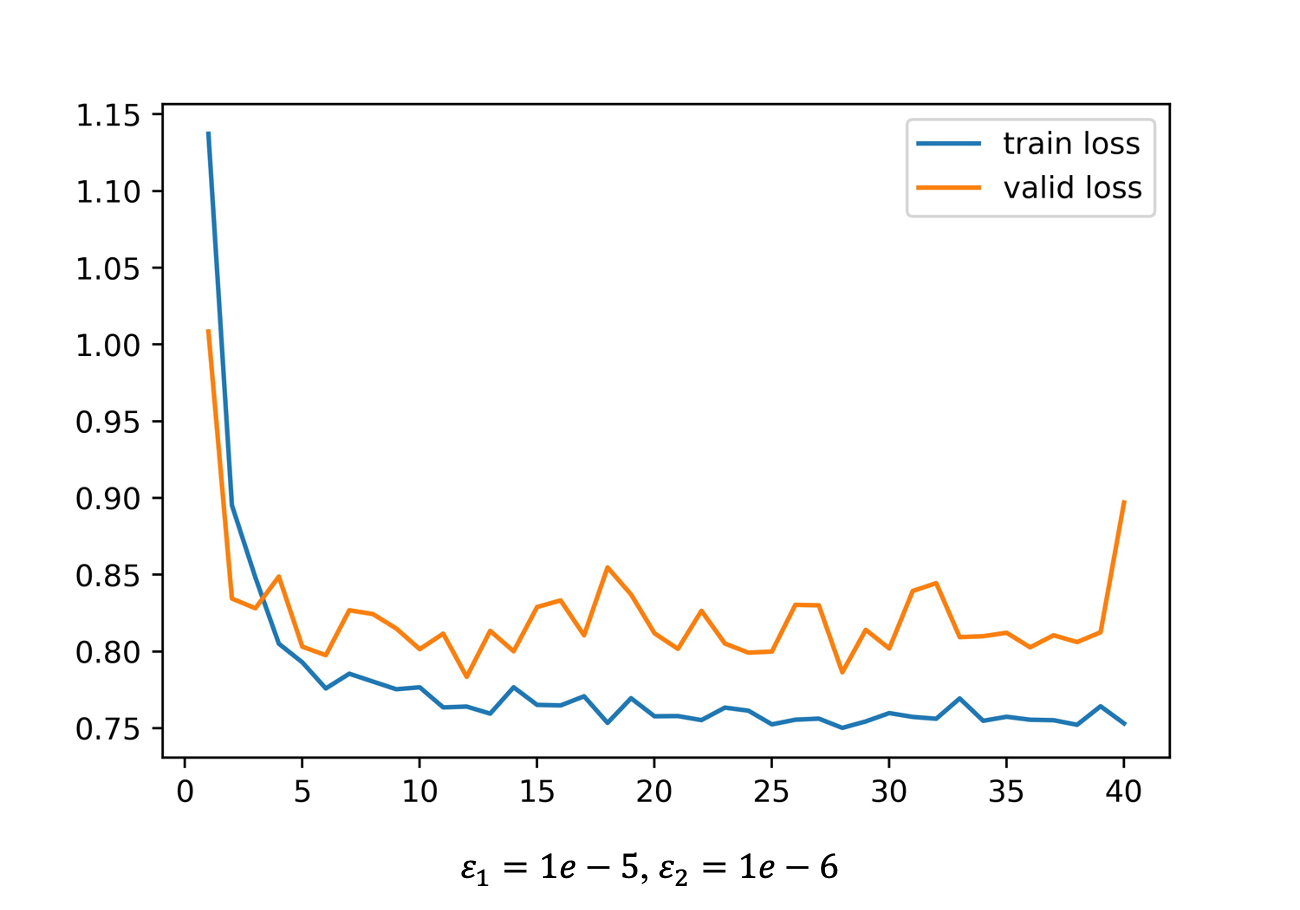
References
我们真的需要把训练集的损失降低到零吗?
LossUpAccUp -Github
https://wmathor.com/index.php/archives/1551/
相关文章:

【机器学习】loss损失讨论
大纲 验证集loss上升,准确率也上升(即将overfitting?)训练集loss一定为要为0吗 Q1. 验证集loss上升,准确率也上升 随着置信度的增加,一小部分点的预测结果是错误的(log lik 给出了指数级的惩…...

LeetCode 779. 第K个语法符号【递归,找规律,位运算】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
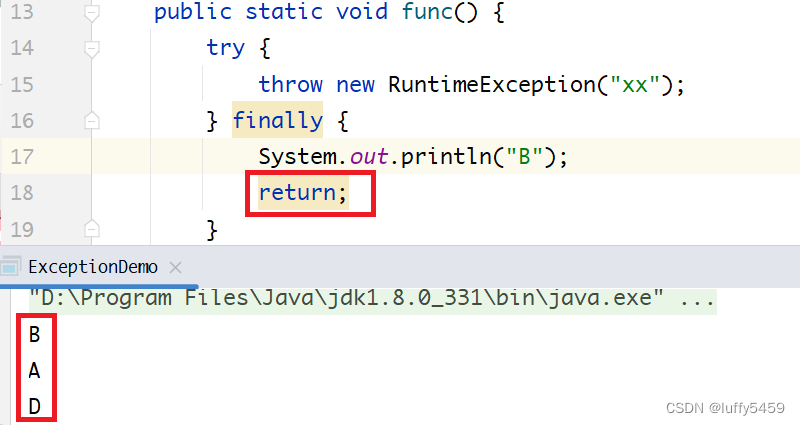
java try throw exception finally 遇上 return break continue造成异常丢失
如下所示,是一个java笔试题,考察的是抛出异常之后,程序运行结果,但是这里抛出异常,并没有捕获异常,而是通过finally来进行了流程控制处理。 package com.xxx.test;public class ExceptionFlow {public sta…...
+ Spring相关源码)
设计模式——装饰器模式(Decorator Pattern)+ Spring相关源码
文章目录 一、装饰器模式的定义二、个人理解举个抽象的例(可能并不是很贴切) 三、例子1、菜鸟教程例子1.1、定义对象1.2、定义装饰器 3、JDK源码 ——包装类4、JDK源码 —— IO、OutputStreamWriter5、Spring源码 —— BeanWrapperImpl5、SpringMVC源码 …...
MATLAB R2018b详细安装教程(附资源)
云盘链接: pan.baidu.com/s/1SsfNtlG96umfXdhaEOPT1g 提取码:1024 大小:11.77GB 安装环境:Win10/Win8/Win7 安装步骤: 1.鼠标右击【R2018b(64bit)】压缩包选择【解压到 R2018b(64bit)】 2.打开解压后的文件夹中的…...
GEE错误——影像加载过程中出现的图层无法展示的解决方案
问题: // I dont know if some standard value exists for the radius, in the same, I will assume that some software would prefer to use square shape, but circle makes more sense to me. // pixels is noice if you want to zoom in and out to visualize…...
读图数据库实战笔记03_遍历
1. Gremlin Server只将数据存储在内存中 1.1. 如果停止Gremlin Server,将丢失数据库里的所有数据 2. 概念 2.1. 遍历(动词) 2.1.1. 当在图数据库中导航时,从顶点到边或从边到顶点的移动过程 2.1.2. 类似于在关系数据库中的查…...

QT如何检测当前系统是是Windows还是Uninx或Mac?以及是哪个版本?
简介 通过Qt获取当前系统及版本号,需要用到QSysInfo。 QSysInfo类提供有关系统的信息。 WordSize指定了应用程序编译所在的平台的指针大小。 ByteOrder指定了平台是大端序还是小端序。 某些常量仅在特定的平台上定义。您可以使用预处理器符号Q_OS_WIN和Q_OS_MACOS来…...
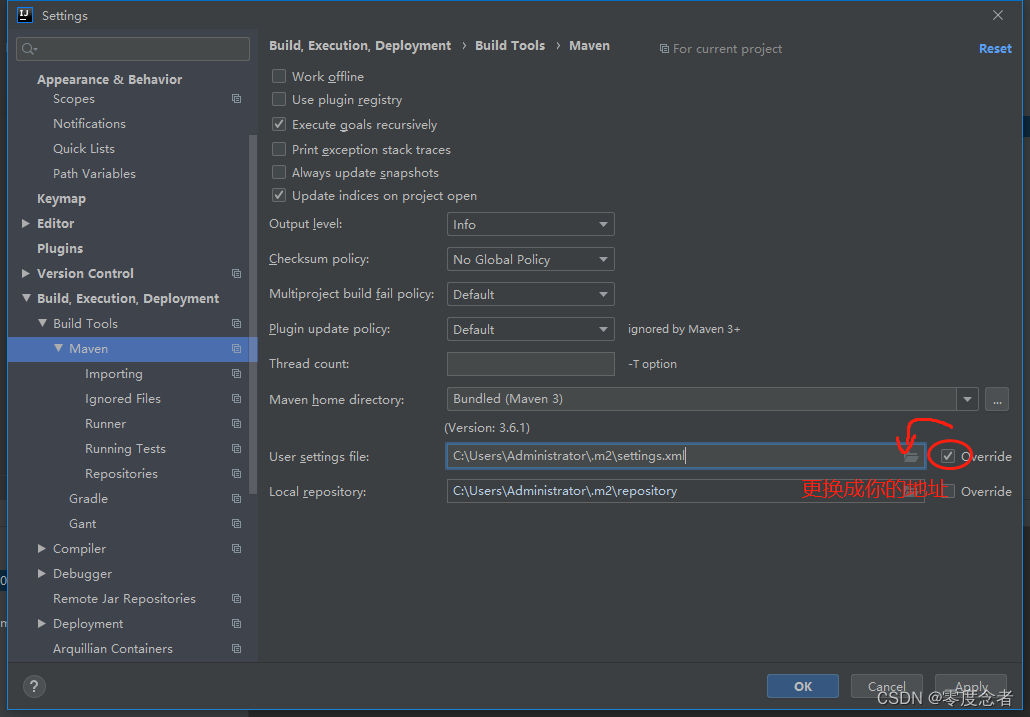
Maven配置阿里云中央仓库settings.xml
Maven配置阿里云settings.xml 前言一、阿里云settings.xml二、使用步骤1.任意目录创建settings.xml2.使用阿里云仓库 总结 前言 国内网络从maven中央仓库下载文件通常是比较慢的,所以建议配置阿里云代理镜像以提高jar包下载速度,IDEA中我们需要配置自己…...

由浅入深C系列八:如何高效使用和处理Json格式的数据
如何高效使用和处理JSON格式的数据 问题引入关于CJSON示例代码头文件引用处理数据 问题引入 最近的项目在用c处理后台的数据时,因为好多外部接口都在使用Json格式作为返回的数据结构和数据描述,如何在c中高效使用和处理Json格式的数据就成为了必须要解决…...
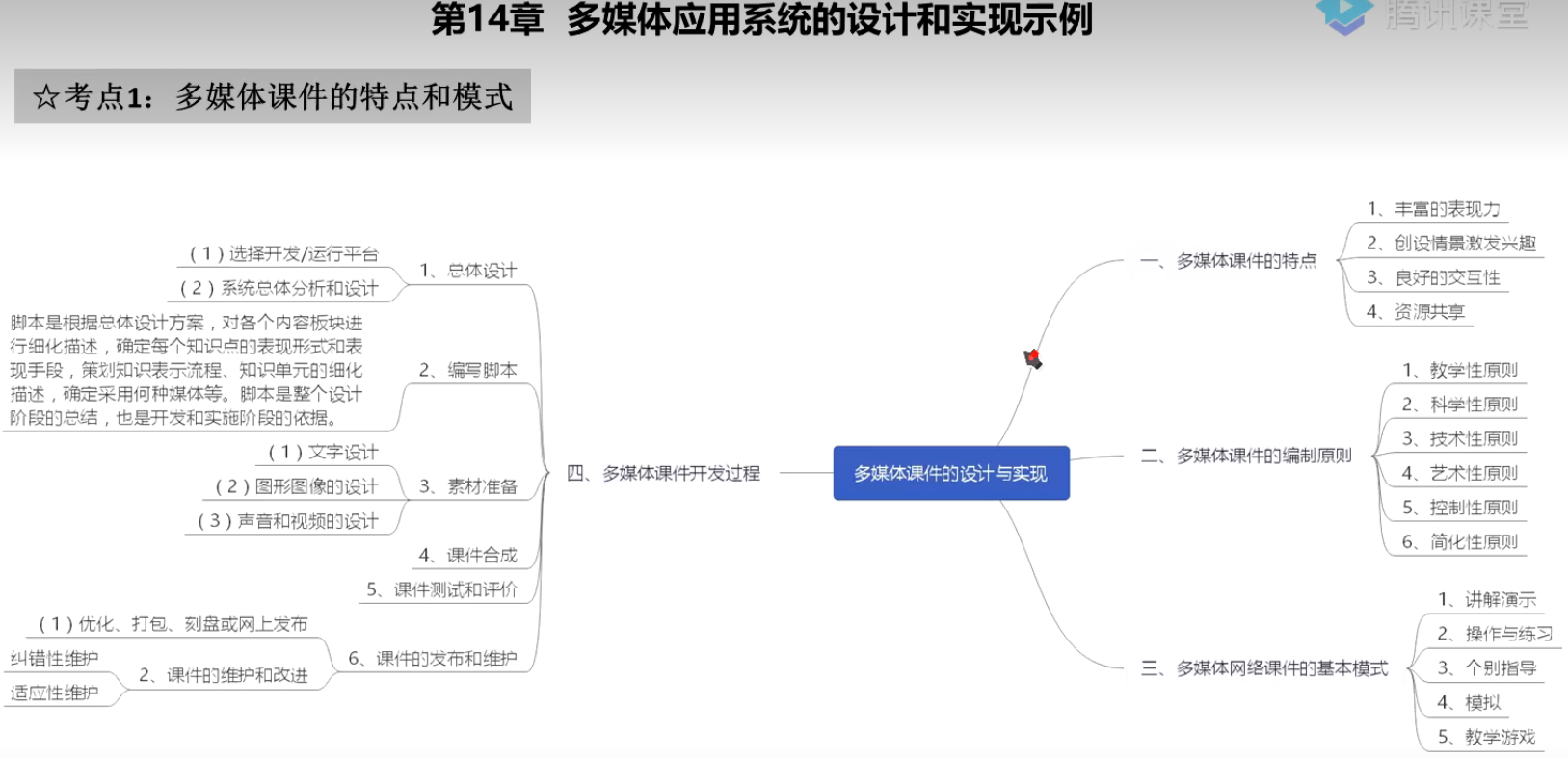
多媒体应用设计师 第16章 多媒体应用系统的设计和实现示例
口诀 思维导图 2020...

golang平滑重启库overseer实现原理
overseer主要完成了三部分功能: 1、连接的无损关闭,2、连接的平滑重启,3、文件变更的自动重启。 下面依次讲一下: 一、连接的无损关闭 golang官方的net包是不支持连接的无损关闭的,当主监听协程退出时,…...
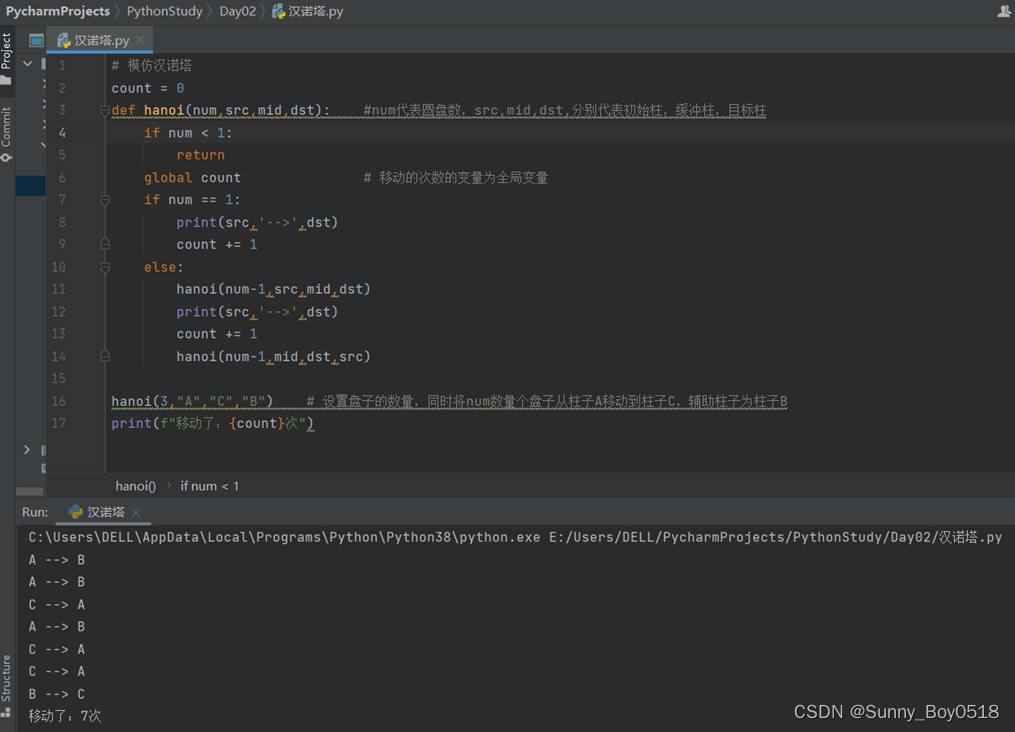
用Python定义一个函数,用递归的方式模拟汉诺塔问题
【任务需求】 定义一个函数,用递归的方式模拟汉诺塔问题,三个柱子,分别为A、B、C,其中A柱子上有N个盘子,从小到大编号为1到N,盘子大小不同。现在要将这N个盘子从A柱子移动到C柱子上,但移动的过…...

二手的需求
案例1030 某天项目经理小王,从用户现场带回了需求,以图形的方式,交给了产品经理。告诉他就照这样设计,结果是项目经理放弃让产品经理出效果图。 原因是产品经理觉得项目经理带回来的需求有问题。项目经理解释产品经理不接受&…...
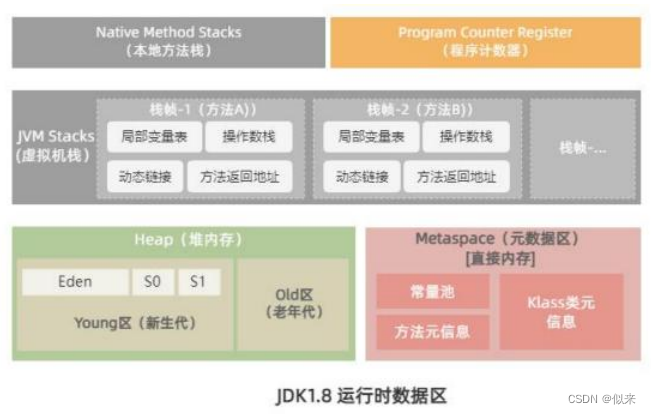
大厂面试题-JVM为什么使用元空间替换了永久代?
目录 面试解析 问题答案 面试解析 我们都知道Java8以及以后的版本中,JVM运行时数据区的结构都在慢慢调整和优化。但实际上这些变化,对于业务开发的小伙伴来说,没有任何影响。 因此我可以说,99%的人都回答不出这个问题。 但是…...
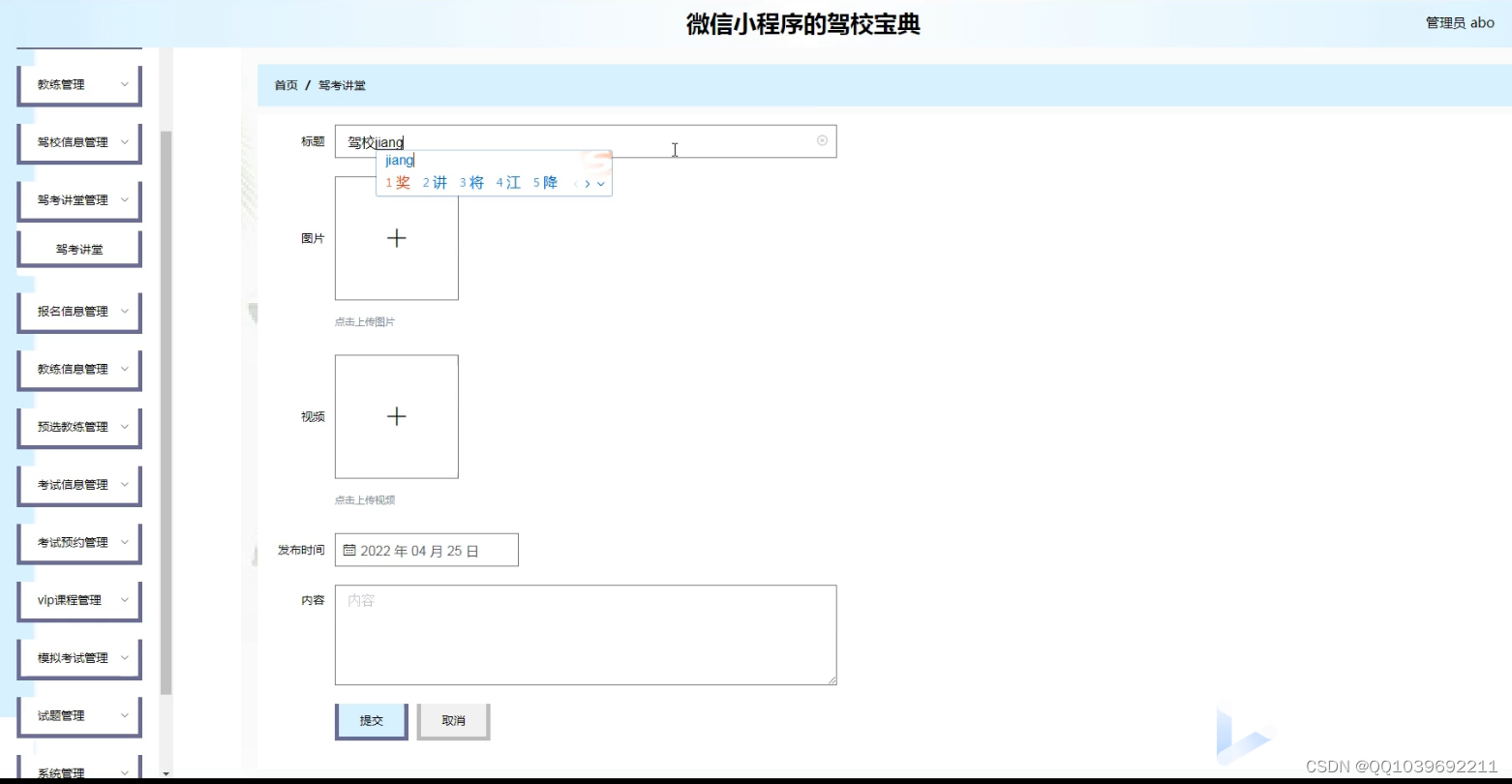
基本微信小程序的驾校宝典系统-驾照考试系统
项目介绍 系统模块分析是对系统的各个模块做出相应的说明以及解释。此系统的模块分别有用户模块、服务端模块和管理端模块这两大基本模块,其中服务端模块包括了首页、教练信息、教练咨讯、考试预约、我的等;而管理端模块则包括了个人中心、用户管理、教…...
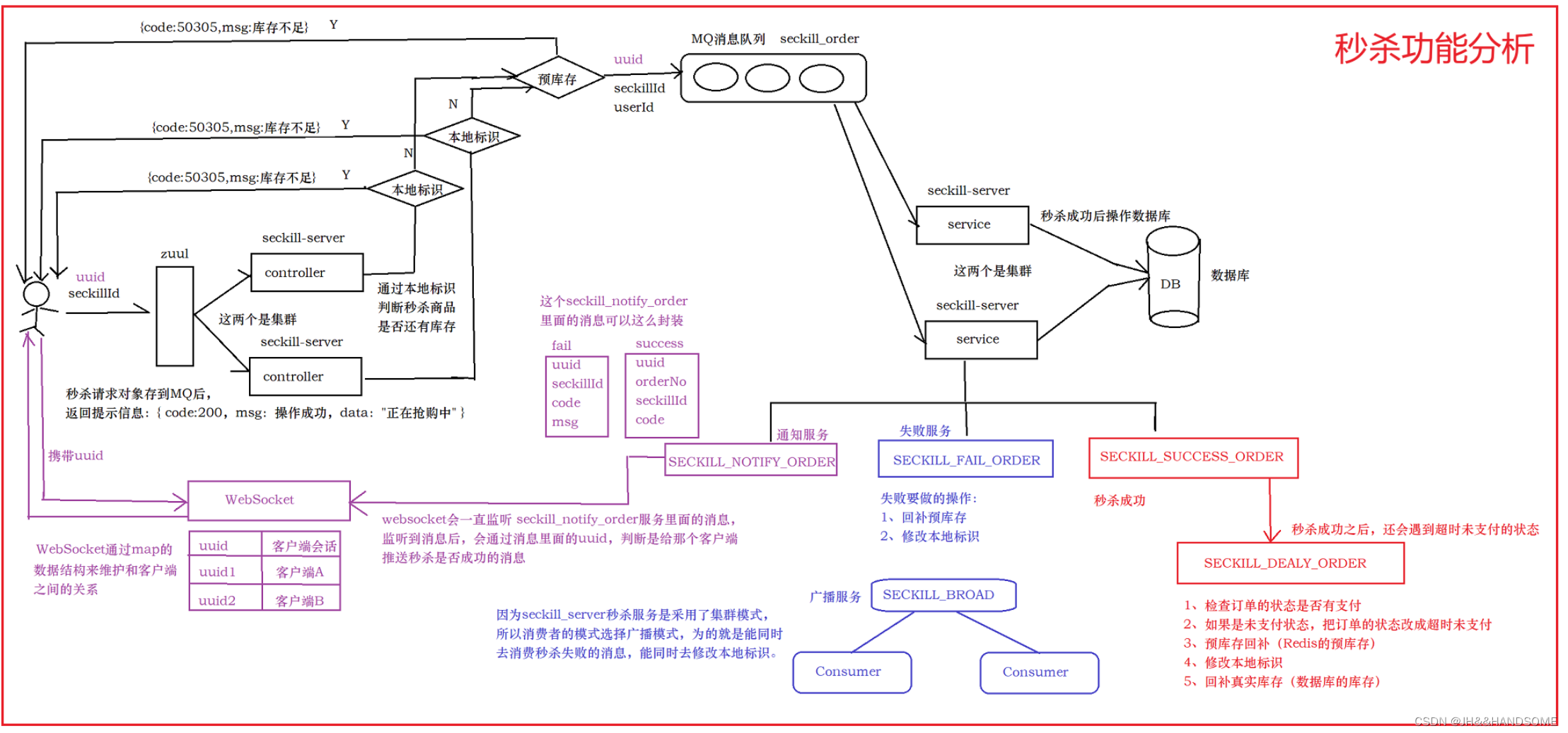
02、SpringCloud -- Redis和Cookie过期时间刷新功能
目录 需求:代码流程过滤器类工具类过滤判断远程调用feign接口gitee 配置接口实现过滤器run方法测试:问题:秒杀功能完整分析图 需求: cookie应该写在网关中,网关中可以自定义filter过滤器,用来实现cookie的刷新和redis中key的刷新,延长用户的操作时间。 就是让用户每操…...

【报错】kali安装ngrok报错解决办法(zsh: exec format error: ./ngrok)
问题描述 kali安装ngrok令牌授权失败 在安装配置文件的时候报错:zsh: exec format error: ./ngrok 原因分析: 在Kali Linux上执行./ngrok时出现zsh exec格式错误的问题可能是由于未安装正确版本的ngrok或操作系统不兼容ngrok导致的。以下是一些可能的解…...

<学习笔记>从零开始自学Python-之-常用库篇(十三)内置小型数据库shelve
一、shelve简介: shelve是Python当中数据储存的方案,类似key-value数据库,便于保存Python对象,shelve只有一个open()函数,用来打开指定的文件(字典),会返回一…...

Redis快速上手篇七(集群-六台虚拟机)
Redis集群 主从复制的场景无法吗满足主机单点故障时需要引入集群配置 一般数据库要处理的读请求远大于写请求 ,针对这种情况,我们优化数据库可以采用读写分离的策略。我们可以部 署一台主服务器主要用来处理写请求,部署多台从服务器 &#…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
